AGC DSP n n Digital Filter Specifications Only

AGC DSP n n Digital Filter Specifications Only the magnitude approximation problem Four basic types of ideal filters with magnitude responses as shown below (Piecewise flat) Professor A G Constantinides 1

AGC DSP n Digital Filter Specifications These filters are unealisable because (one of the following is sufficient) n their impulse responses infinitely long noncausal n Their amplitude responses cannot be equal to a constant over a band of frequencies Another perspective that provides some understanding can be obtained by looking at the ideal amplitude squared. Professor A G Constantinides 2

AGC DSP n Digital Filter Specifications Consider the ideal LP response squared (same as actual LP response) Professor A G Constantinides 3

AGC DSP n n n Digital Filter Specifications The realisable squared amplitude response transfer function (and its differential) is continuous in Such functions n if IIR can be infinite at point but around that point cannot be zero. n if FIR cannot be infinite anywhere. Hence previous defferential of ideal response is unrealisable Professor A G Constantinides 4

AGC DSP n n Digital Filter Specifications A realisable response would effectively need to have an approximation of the delta functions in the differential This is a necessary condition Professor A G Constantinides 5

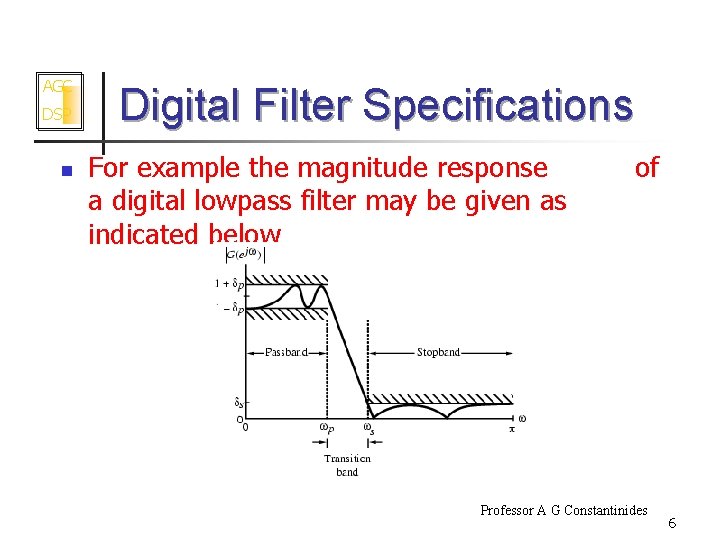
AGC DSP n Digital Filter Specifications For example the magnitude response of a digital lowpass filter may be given as indicated below Professor A G Constantinides 6

AGC DSP n n Digital Filter Specifications In the passband we require that with a deviation In the stopband we require that with a deviation Professor A G Constantinides 7

AGC DSP Digital Filter Specifications Filter specification parameters n - passband edge frequency n - stopband edge frequency n - peak ripple value in the passband n - peak ripple value in the stopband Professor A G Constantinides 8

AGC Digital Filter Specifications DSP Practical specifications are often given in terms of loss function (in d. B) n n Peak passband ripple d. B n Minimum stopband attenuation d. B n Professor A G Constantinides 9

Digital Filter Specifications AGC DSP n n In practice, passband edge frequency and stopband edge frequency are specified in Hz For digital filter design, normalized bandedge frequencies need to be computed from specifications in Hz using Professor A G Constantinides 10

AGC Digital Filter Specifications DSP n n Example - Let k. Hz, and k. Hz Then Professor A G Constantinides 11

Selection of Filter Type AGC DSP n n n The transfer function H(z) meeting the specifications must be a causal transfer function For IIR real digital filter the transfer function is a real rational function of H(z) must be stable and of lowest order N or M for reduced computational complexity Professor A G Constantinides 12

AGC DSP n n Selection of Filter Type FIR real digital filter transfer function is a polynomial in (order N) with real coefficients For reduced computational complexity, degree N of H(z) must be as small as possible If a linear phase is desired then we must have: Professor A G Constantinides (More on this later) 13

AGC DSP n n Selection of Filter Type Advantages in using an FIR filter (1) Can be designed with exact linear phase (2) Filter structure always stable with quantised coefficients Disadvantages in using an FIR filter - Order of an FIR filter is considerably higher than that of an equivalent IIR filter meeting the same specifications; this leads to higher computational complexity for FIR Professor A G Constantinides 14

AGC DSP FIR Design FIR Digital Filter Design Three commonly used approaches to FIR filter design (1) Windowed Fourier series approach (2) Frequency sampling approach (3) Computer-based optimization methods Professor A G Constantinides 15

Finite Impulse Response Filters AGC DSP n n The transfer function is given by The length of Impulse Response is N All poles are at . Zeros can be placed anywhere on the zplane Professor A G Constantinides 16

AGC DSP FIR: Linear phase For phase linearity the FIR transfer function must have zeros outside the unit circle Professor A G Constantinides 17

AGC FIR: Linear phase DSP n n n To develop expression for phase response set transfer function (order n) In factored form Where , is real & zeros occur in conjugates Professor A G Constantinides 18

AGC FIR: Linear phase DSP n n Let where Thus Professor A G Constantinides 19

AGC FIR: Linear phase DSP Expand in a Laurent Series convergent within the unit circle n To do so modify the second sum as n Professor A G Constantinides 20

AGC FIR: Linear phase DSP n So that n Thus n where Professor A G Constantinides 21

AGC FIR: Linear phase DSP n n n are the root moments of the minimum phase component are the inverse root moments of the maximum phase component Now on the unit circle we have and Professor A G Constantinides 22

AGC Fundamental Relationships DSP n hence (note Fourier form) Professor A G Constantinides 23

AGC FIR: Linear phase DSP n n Thus for linear phase the second term in the fundamental phase relationship must be identically zero for all index values. Hence 1) the maximum phase factor has zeros which are the inverses of the those of the minimum phase factor 2) the phase response is linear with group delay (normalised) equal to the number of zeros outside the unit circle Professor A G Constantinides 24

AGC FIR: Linear phase DSP n It follows that zeros of linear phase FIR trasfer functions not on the circumference of the unit circle occur in the form Professor A G Constantinides 25

AGC FIR: Linear phase DSP n n n For Linear Phase t. f. (order N-1) so that for N even: Professor A G Constantinides 26

AGC FIR: Linear phase DSP n n for N odd: I) On we have for N even, and +ve sign Professor A G Constantinides 27

AGC FIR: Linear phase DSP n n n II) While for –ve sign [Note: antisymmetric case adds rads to phase, with discontinuity at ] III) For N odd with +ve sign Professor A G Constantinides 28

AGC FIR: Linear phase DSP n n IV) While with a –ve sign [Notice that for the antisymmetric case to have linear phase we require The phase discontinuity is as for N even] Professor A G Constantinides 29

AGC FIR: Linear phase DSP n The cases most commonly used in filter design are (I) and (III), for which the amplitude characteristic can be written as a polynomial in Professor A G Constantinides 30

AGC DSP Design of FIR filters: Windows (i) Start with ideal infinite duration (ii) Truncate to finite length. (This produces unwanted ripples increasing in height near discontinuity. ) (iii) Modify to Weight w(n) is the window Professor A G Constantinides 31

AGC Windows DSP n n n Commonly used windows Rectangular Bartlett Hann Hamming Blackman n n Kaiser Professor A G Constantinides 32

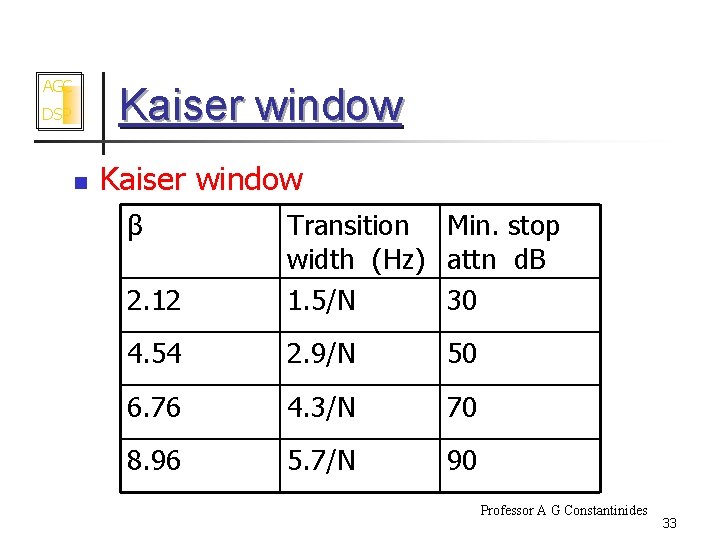
AGC Kaiser window DSP n Kaiser window β 2. 12 Transition Min. stop width (Hz) attn d. B 1. 5/N 30 4. 54 2. 9/N 50 6. 76 4. 3/N 70 8. 96 5. 7/N 90 Professor A G Constantinides 33

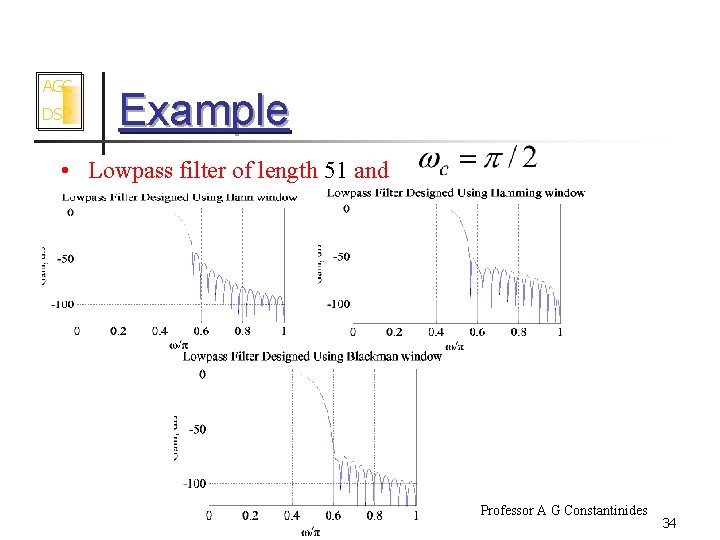
AGC DSP Example • Lowpass filter of length 51 and Professor A G Constantinides 34

AGC DSP Frequency Sampling Method • In this approach we are given and need to find • This is an interpolation problem and the solution is given in the DFT part of the course • It has similar problems to the windowing Professor A G Constantinides approach 35

Linear-Phase FIR Filter Design by Optimisation AGC DSP n Amplitude response for all 4 types of linear-phase FIR filters can be expressed as where Professor A G Constantinides 36

Linear-Phase FIR Filter Design by Optimisation AGC DSP n Modified form of weighted error function where Professor A G Constantinides 37

AGC DSP n n Linear-Phase FIR Filter Design by Optimisation Problem - Determine which minimise the peak absolute value of over the specified frequency bands After has been determined, construct the original and hence h[n] Professor A G Constantinides 38

AGC DSP Linear-Phase FIR Filter Design by Optimisation Solution is obtained via the Alternation Theorem The optimal solution has equiripple behaviour consistent with the total number of available parameters. Parks and Mc. Clellan used the Remez algorithm to develop a procedure for designing linear FIR digital filters. Professor A G Constantinides 39

AGC DSP FIR Digital Filter Order Estimation Kaiser’s Formula: n ie N is inversely proportional to transition band width and not on transition band location Professor A G Constantinides 40

AGC DSP n FIR Digital Filter Order Estimation Hermann-Rabiner-Chan’s Formula: where with Professor A G Constantinides 41

AGC DSP n n FIR Digital Filter Order Estimation Formula valid for For , formula to be used is obtained by interchanging and Both formulae provide only an estimate of the required filter order N If specifications are not met, increase filter order until they are met Professor A G Constantinides 42

AGC DSP n n FIR Digital Filter Order Estimation Fred Harris’ guide: where A is the attenuation in d. B Then add about 10% to it Professor A G Constantinides 43