Affine and Substitution ciphers Number Theory gcd Euler

- Affine and Substitution ciphers - Number Theory: gcd, Euler phi function, Euclidean and extended Euclidean algorithms Classical Ciphers – 2 CSCI 284 Spring 2004 GWU CS 284/Spring 04/GWU/Vora/Classical Ciphers

Questions on HW? Project? • Second module requires other input: – m, the modulus – the message is 50 symbols modulo m, each a 10 -bit symbol • Project proposals due: March 1 • Exceptions due: Feb 9 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 2
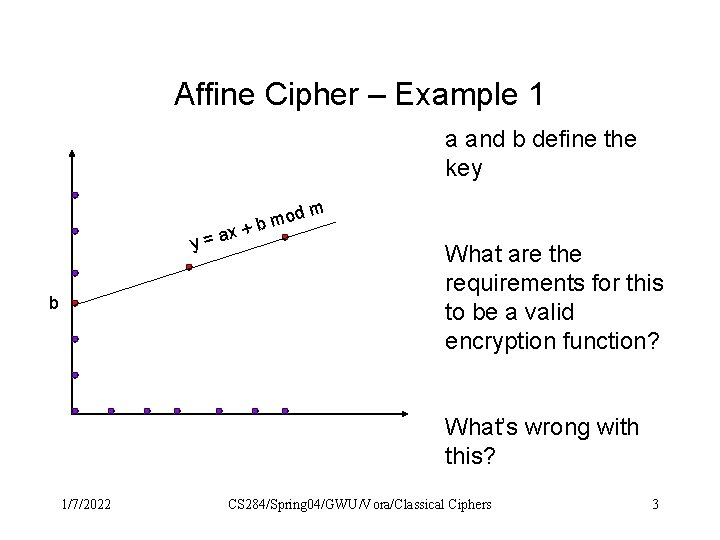
Affine Cipher – Example 1 a and b define the key dm mo b + x y=a b What are the requirements for this to be a valid encryption function? What’s wrong with this? 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 3
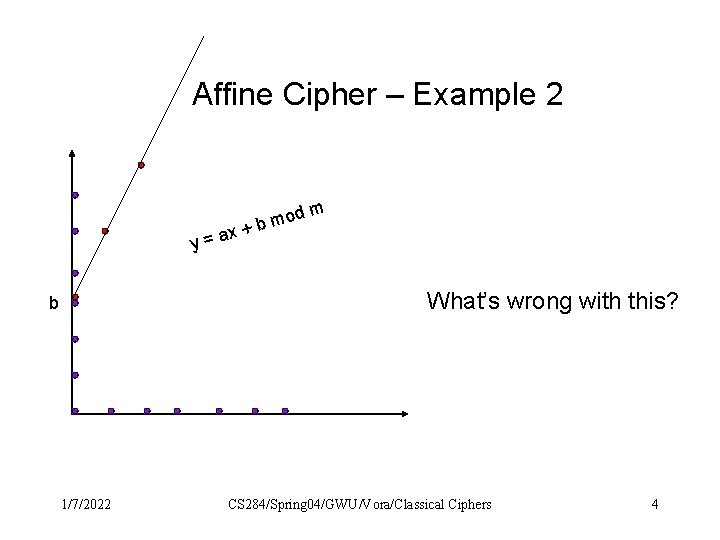
Affine Cipher – Example 2 dm mo b + x y=a What’s wrong with this? b 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 4

Affine Cipher – Example 3 What’s wrong with this? b 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 5

Try m=6, b=1, check all a y = ax + b = ax + 1 mod 6 a=1 y = x + 1 mod 6; x = y-1 mod 6 a=2 y = 2 x +1 mod 6; x = 2 -1(y-1) mod 6 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 6

Affine cipher - definition e(x) = ax + b mod m d(y) = a-1(y-b) mod m Is this possible for all a? Try on example: m = 6. Find a-1 for all a Zm 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 7

GCD: definition The gcd (Greatest Common Divisor) of two integers m and n denoted gcd(m, n) is the largest non-negative integer that divides both m and n. 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 8

Properties of integers - I Fact 1: gcd(m, n) = 1 integers a, b, such that am + bn = 1 Proof: Need to show: 1. Suppose gcd(m, n) = 1 a, b, such that am + bn = 1 2. Suppose a, b, such that am + bn = 1 gcd(m, n) = 1 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 9

Proof of: gcd(m, n) = 1 a, b, such that am + bn = 1 Suppose gcd(m, n) = 1 Let k be any integer of the form Am + Bn for integers A and B Let g be the smallest non-negative integer of this form (want to show g = 1) Then k = Cg + r, 0 r < g 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 10

Proof contd. : gcd(m, n) = 1 a, b, such that am + bn = 1 k = Cg + r, 0 r < g where r = Am + Bn – Cg = Am + Bn – C(A’m +B’n) = A’’m + B’’n =0 (as g was smallest such non-negative integer and r < g) 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 11

Proof contd. : gcd(m, n) = 1 a, b, such that am + bn = 1 k = Cg + r; r = 0 Hence g divides all integers of the form Am + Bn, in particular, g divides m (B = 0) and n (A = 0) g = 1 (as gcd(m, n) = 1) a, b, such that am + bn = 1 (as g is of form Am + Bn) 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 12

Proof of: a, b, such that am + bn = 1 gcd(m, n) = 1 2. Suppose a, b, such that am + bn = 1 gcd(m, n) divides m and n Hence it divides am + bn for all a, b Hence it divides 1 gcd(m, n) = 1 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 13

Theorem: multiplicative inverse in a commutative ring The multiplicative inverse of a mod m Zm exists if and only if gcd(a, m) = 1. It is denoted a-1 Proof: Suppose gcd(a, m) = 1 integers x, y, such that ax + my = 1 ax 1 (mod m) x = a-1 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 14

Theorem: multiplicative inverse in a commutative ring – contd. The multiplicative inverse of a mod m Zm exists if and only if gcd(a, m) = 1. It is denoted a-1 Proof: Suppose a-1 exists, call it X a. X 1 (mod m) a. X + Ym = 1 for some integer Y gcd(a, m) = 1 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 15

Affine Cipher P = C = Zm K = {(a, b) Zm X Zm gcd(a, m) =1} e. K(x) = (ax+b) mod m d. K(y) = a-1(y-b) mod m 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 16

Affine cipher examples Encrypt firstletstrythekasiskitest Using key: 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 17

Cryptanalysis of the Affine Cipher OZOBDNEYOUEYHOBITJOTMBQTOVV QQAUWNMTIQIQTAYQRVEUSQJMQ HONABTQXNMZACOIOBXQEJAHONS QEBTJAQTNAATRITJAYOMVREFOTT JAAXGAEDTJAVOCBJAVAOXQYOFM BAWHTJADVOGQTEBAHOTJNMBGM BGTJARAVVRAUOWQAJMQHONABT QOVCOIQSAAHTJADNEBTXEENVEU SAX. 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 18

Ciphertext frequency A 27 O 21 T 20 Q 18 J 13 B 13 E 12 V 11 N 10 M 9 H 7 X 6 I 6 R 5 U 5 Y 5 D 4 G 4 S 4 C 3 W 3 Z 2 F 2 P 0 K 0 L 0 English language frequency per 1000 e 127 t 91 a 82 o 75 i 70 n 67 s 63 h 61 r 60 d 43 l 40 c 28 u 28 m 24 w 23 f 22 g 20 y 20 p 19 b 15 v 10 k 8 j 2 q 1 x 1 z 1 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 19

Complexity of attacks Brute Force attack for alphabet of size n How difficult is it to break this? How many possible keys? m 2? m? 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 20

Examples • If m = p, p – 1 invertible elements • If m = pq, 1, 2, 3, …p, . . 2 p, . . 3 p, …qp q numbers divisible by p 1, 2, 3, …q, . . 2 q, . . 3 q, …pq p numbers divisible by q pq only number counted twice. No other numbers. pq – p – q + 1 = (p-1)(q-1) invertible elements What if m = i=1 r piei 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 21

Need induction • How do we show that 1+2+3 …. +n = (n+1)n/2 • How do we show that a+ar+ar 2+ar 3 … +arn = a(rn+1 -1)/r-1 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 22

Euler phi function Number of invertible elements of Zm for m = i=1 r piei is Euler “phi” or “totient” function: (m) = i=1 r piei -1(pi -1) Examples: (180), (24) 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 23

Theorem: number of invertible elements in a commutative ring Proof by induction over r - First we show it is true for r=1 i. e. if m = pe Exactly one pth of the numbers are divisible by p (pe) = pe – pe-1 = pe-1(p-1) 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 24

Theorem: number of invertible elements in a commutative ring Now, assume true for r=k, show true for r=k+1 i. e. add one more new prime raised to any power ( i=1 k piei ) = i=1 k piei -1(pi -1) ( i=1 k+1 piei ) = ? Note: we also know (pe) = pe-1(p-1) i. e. what is (xy) when (x) and (y) are known, and x and y are relatively prime 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 25
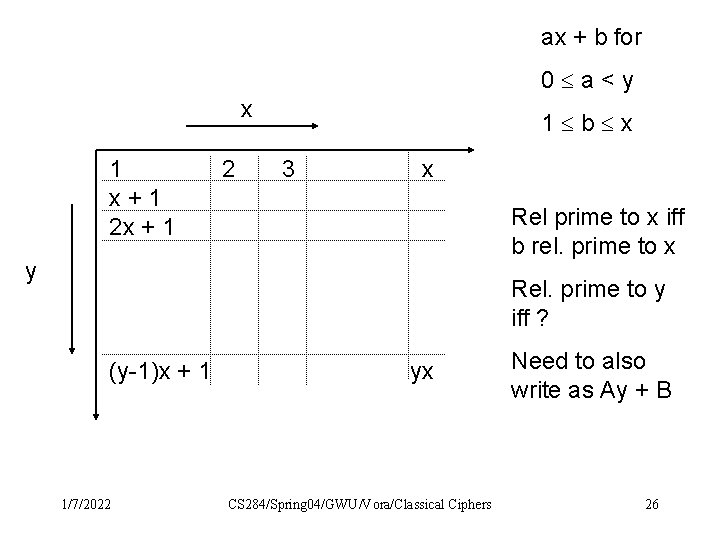
ax + b for 0 a<y x 1 x+1 2 x + 1 2 1 b x 3 x Rel prime to x iff b rel. prime to x y Rel. prime to y iff ? (y-1)x + 1 1/7/2022 yx CS 284/Spring 04/GWU/Vora/Classical Ciphers Need to also write as Ay + B 26

Chinese Remainder Theorem There is exactly one number modulo xy which is bmodx and Bmody if x and y are relatively prime. Proof: Suppose not. Then: ax + b = Ay + B cx + b = Cy + B (a-c)x = (A-C)y y | (a-c)x y | (a-c) because x and y rel. prime a = my + c first number = mxy + cx + b = second number modulo xy 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 27

Now look at ring Zm when m = xy Size of ring is xy. See numbers mod x: x of them Numbers mod y: y of them Thus, a number mod m is represented uniquely by the pair: (a, b) (its remainder modx, and remainder mod y) A number is rel. prime to both x and y iff a and b are rel. prime to x and y respectively There are (x) (y) numbers rel. prime to xy 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 28

Back to Euler ( i=1 k piei ) = i=1 k piei -1(pi -1) ( i=1 k+1 piei ) = ? Note: we also know (pe) = pe-1(p-1) 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 29

Problems from text 1. 11: An involutory key is defined as the key for which the encryption function is identical to the decryption function. (a) Suppose that K = (a, b) is a key in an Affine Cipher over Zn Prove that K is an involutory key if and only if a-1 mod n = a and b(a+1) 0 (mod n) (b) Determine all the involutory keys in the affine cipher over Z 15 (c) Suppose that n = pq, where p and q are distinct odd primes. Prove that the number of involutory keys in the Affine Cipher over Zn is n+p+q+1 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 30

How do we generate an encryption key for an affine cipher? 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 31

Euclidean Algorithm considered first non-trivial algorithm gcd(m, n) /* m > n */ (a, b) : = (m, n) /* Initialize */ while (b 0) (a, b) : = (b, a – b*q) /*Where q = a/b */ return(a) Works because: gcd(a, b) = gcd(b, a – b* a/b ) gcd(a, b) = b if b|a 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 32

Try gcd(17, 101) gcd(57, 93) 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 33

Proof that Euclidean algorithm works For ith step, (a, b)i say total k steps (a, b)0 = (m, n) (a, b)k-1 = ( b, b) 1. Prove that: gcd(m, n) = gcd(a, b)i 2. Prove that it stops 3. Hence: 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 34

Extended Euclidean algorithm Find s, t such that gcd(m, n) = sm +tn Let gcd(a, b)i = siai + tibi 1. Last but one step: bk-1|ak-1 gcd(a, b)k-1 = bk-1 sk-1=0; tk-1=1 2. In general: If gcd(a, b)i = siai + tibi What is: si-1 ti-1? 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 35

Extended Euclidean algorithm bk-1 = gcd(a, b)i-1 = siai + tibi = sibi-1 + ti(ai-1 – bi-1*qi-1) = tiai-1 + (si – ti*qi-1) bi-1 So, si-1 = ti and ti-1 = si – ti*qi-1 Go back up the euclidean algorithm: (s, t) : = (0, 1) /* Initialize */ while (b 0) (s, t) : = (t, s-t*q) return((s, t)) 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 36

Examples gcd(17, 101) gcd(57, 93) What good? Write algorithm for multiplicative inverse of x mod m 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 37

Solve congruences What is x? 17 x 3 mod 101 5 x 2 mod 7 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 38

Euclidean Algorithm: References See Text, section 5. 2. 1 http: //www. uoregon. edu/~koch/math 233/Euclid. pdf http: //www. nku. edu/~christensen/031 MAT 494 euclid. doc 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 39

Substitution Cipher Each letter goes to another Key is the lookup table, consists of 2 n elements for alphabet size n Statistical attacks Brute force attack requires: 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 40

Problem • A particular letter goes to a fixed other letter. Monoalphabetic cipher • Need polyalphabetic ciphers 1/7/2022 CS 284/Spring 04/GWU/Vora/Classical Ciphers 41
- Slides: 41