Aerial Remote Sensing Parallax Definition Parallax Monoscopic and

Aerial Remote Sensing Parallax Definition Parallax : Monoscopic and Stereoscopic Parallax Equitation for vertical Aerial Photo Height Determination Using Parallax Bar • Dr R. Jegankumar. M. Sc. , M. Tech. , Ph. D. , • Assistant Professor & Head • Department of Geography • School of Geosciences • Bharathidasan University • Tiruchirappalli – 620 024

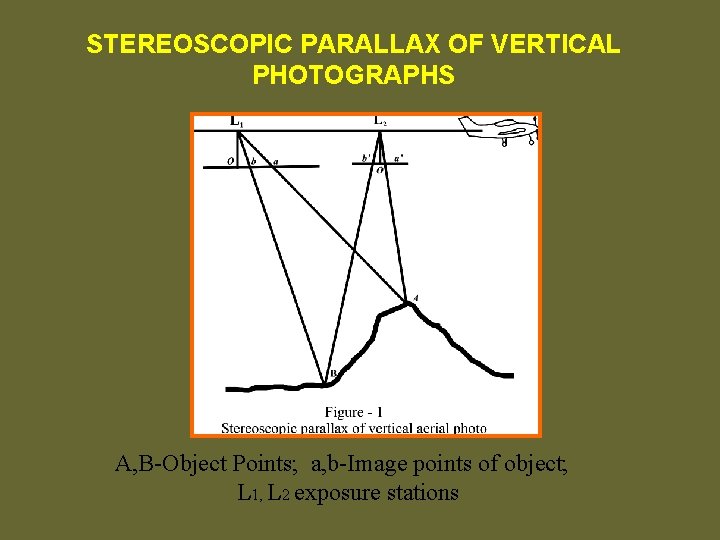
STEREOSCOPIC PARALLAX Parallax is the apparent displacement in the position of an object, with respect to a frame of reference, caused by a shift in the position of observation. v. If a person looked through the viewfinder of an aerial camera as the aircraft moves forward, images of objects would be seen to move across the field of view. v. The closer object is to the cameras, the more its image will appear to move.

STEREOSCOPIC PARALLAX OF VERTICAL PHOTOGRAPHS A, B-Object Points; a, b-Image points of object; L 1, L 2 exposure stations

ØThe parallax of any point is directly related to the elevation of the point. ØThe parallax is greater for high points than for low points. Variation of parallax with elevation provides the Fundamental basis for determining elevations of points from photographic measurements. Pa = xa - xa'

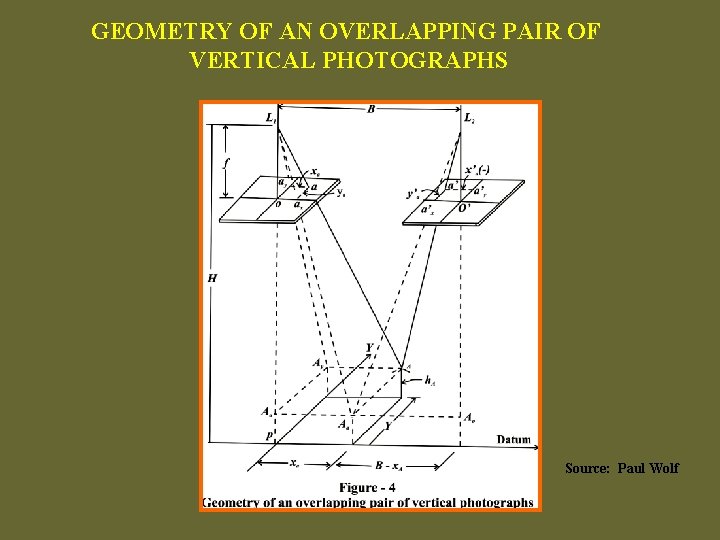
PARALLAX EQUATIONS The figure illustrates an overlapping pair of vertical photographs, which have been exposed at equal flying heights above datum. Images of an object point A appear on the left and right photos at a and a', respectively. The planimetric position of point A on the ground is given in terms of ground coordinates XA and YA. Its elevation above datum is h. A. The XY ground axis system has its origin at the datum principal point P of the left hand photograph; the X axis is in the same vertical plane as the photographic x and x' flight axis passes through the datum principal point of the left photo and is perpendicular to the X axis. According to this definition, each stereopair of photographs has its own unique ground coordinate system.

GEOMETRY OF AN OVERLAPPING PAIR OF VERTICAL PHOTOGRAPHS Source: Paul Wolf

By equating similar triangles of figure , formulas for calculating h. A, XA, and YA may be derived. From similar triangles L 1 oay and L 1 Ao. Ay, YA / H-h. A = ya / f From which YA = ya / f (H – h. A) (a) And equating similar triangles L 1 oax and L 1 Ao. Ax, we have XA / H – h A = x a / f From which XA = xa / f (H – h. A) (b) Also from similar triangles L 2 o’a’x and L 2 A’o. Ax, B – XA / H – h. A = -x'a / f From which XA = B + X'a / f (H – h. A) Source: Paul Wolf (c)

Equating Eqs. (b) and (c) and reducing gives h. A = H - Bf / xa – x’a (d) Substituting Pa for xa – x’a into Eq. (d) yields. h. A = H - Bf / Pa (1) Now substituting Eq. (1) into each of Eqs. (b) and (a) and reducing: XA = B* xa / Pa (2) YA = B* ya / Pa (3) In Eqs. (1), (2) and (3), pa is the parallax of point A, XA and YA are the ground coordinates of point A, xa and ya the photo coordinates of point a measured with respect to the flight-line axes on the left photo. Equation (1), (2) and (3) are commonly called the parallax equations. They are among the most useful equations to the photogrammetrist. These equations enable a complete survey of the overlap area of a stereopair Source: Paul Wolf

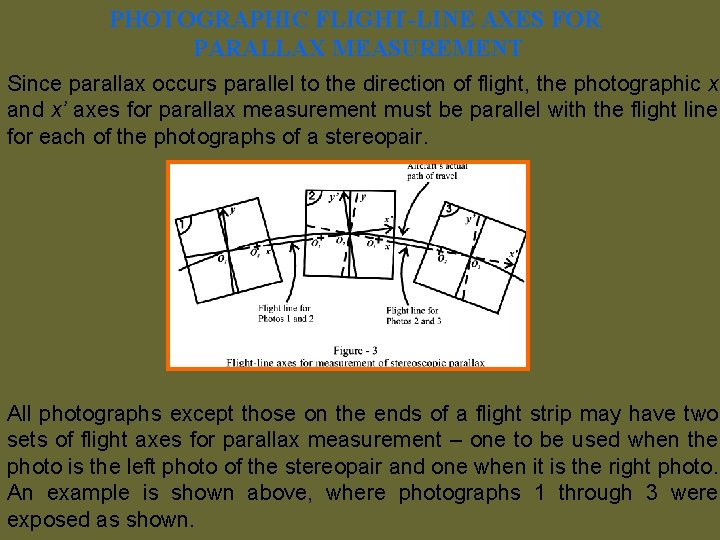
PHOTOGRAPHIC FLIGHT-LINE AXES FOR PARALLAX MEASUREMENT Since parallax occurs parallel to the direction of flight, the photographic x and x’ axes for parallax measurement must be parallel with the flight line for each of the photographs of a stereopair. All photographs except those on the ends of a flight strip may have two sets of flight axes for parallax measurement – one to be used when the photo is the left photo of the stereopair and one when it is the right photo. An example is shown above, where photographs 1 through 3 were exposed as shown.

PHOTOGRAPHIC FLIGHT-LINE AXES FOR PARALLAX MEASUREMENT Parallax measurement in the overlap area of photos 1 and 2 are made with respect to the solid xy axis system of photo 1 and the solid x’y’ system of photo 2 However, due to the aircraft’s curved path of travel, the flight line of photos 2 and 3 is not in the same direction as the flight line of photos 1 and 2. Therefore, parallax measurements in the overlap area of photos 2 and 3 must be made with respect to the dashed xy axis system on photo 2 and the dashed x’y’ system of photo 3. It is possible for the two axis systems to be coincident; however, this does not generally occur in practice.

MONOSCOPIC METHODS OF PARALLAX MEASUREMENT

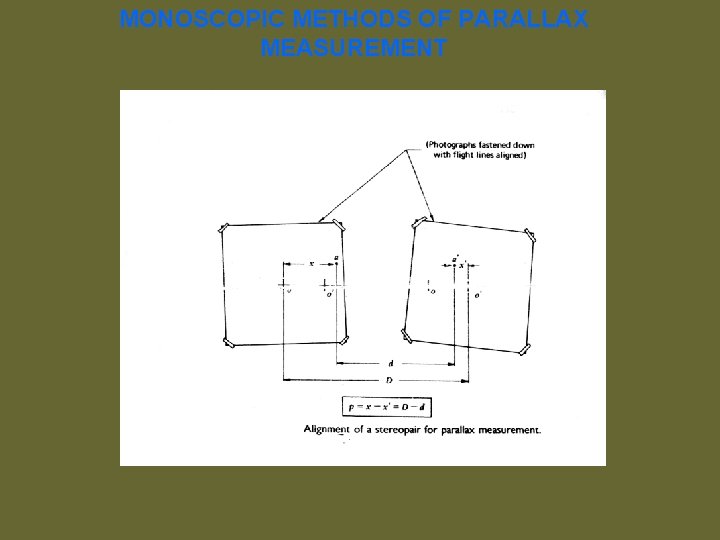
MONOSCOPIC METHODS OF PARALLAX MEASUREMENT Parallaxes of points on a stereopair may be measured either monoscopically or stereoscopically. The distance D between the two principal points is a constant, which can be measured. The parallax of point A is Pa = xa – xa' (In fig xb coordinate is negative). However by examining the figure it is seen the parallax is also. Pa = D – d a Methods of Parallax measurement, A simple scale may be used with the choice being based upon the desired accuracy. The advantage is that for each additional point whose parallax is desired only a single measurement is required with either of these monoscopic A disadvantages of this method is that two measurement are required for each point.

STEREOSCOPIC PARALLAX ØIn the figure above images of object points A and B appears on a pair of overlapping vertical aerial photographs, which were taken from exposure stations L 1 and L 2. A and B are imaged at a and b on the left hand photograph. ØForward motion of the aircraft between exposures, however, caused the images to move laterally across the camera focal plane parallel to the flight line, so that on the right-hand photo they appear at a’ and b’.

STEREOSCOPIC METHODS OF PARALLAX MEASUREMENT ØThrough the principle of the floating mark, parallaxes of points may be measured stereoscopically. This method employs a stereoscope in conjunction with an instrument called a parallax bar, also frequently called a stereo meter. ØThe micrometer readings. parallaxes. or differences in parallax are obtained Ø A parallax bar is shown lying on the photos beneath a mirror stereo

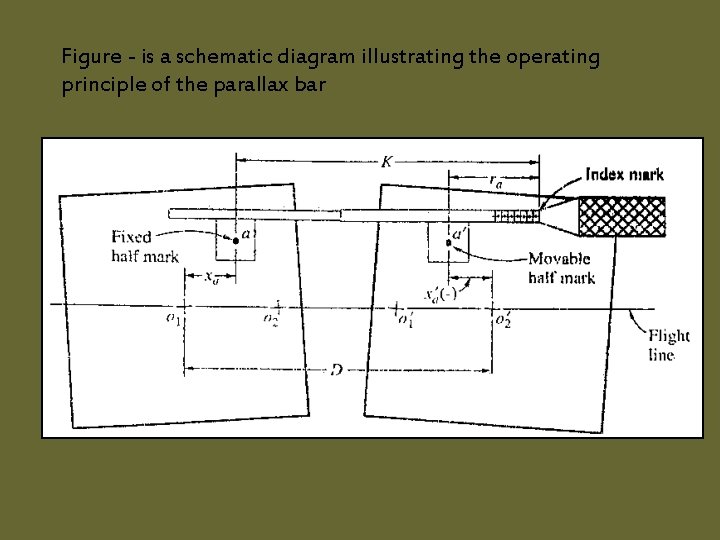
Figure - is a schematic diagram illustrating the operating principle of the parallax bar

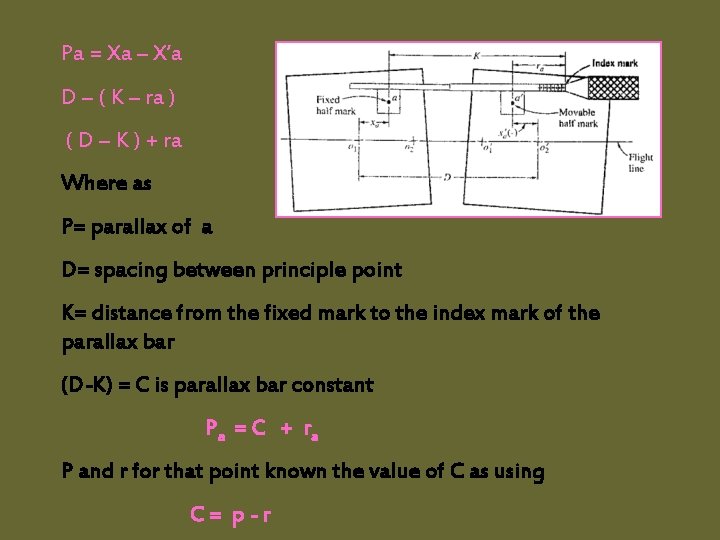
Pa = Xa – X’a D – ( K – ra ) ( D – K ) + ra Where as P= parallax of a D= spacing between principle point K= distance from the fixed mark to the index mark of the parallax bar (D-K) = C is parallax bar constant Pa = C + r a P and r for that point known the value of C as using C= p-r

The parallax bar constant should be determined on the basis of micro meter reading and parallax measurements or two points. The mean of the two values may be adopted. ØAny two points may be selected for this purpose; however they should be clear, discrete images, and selected so that they lie on opposite sides of the flight line and approximately equidistant from the flight line. ØThis minimizes error in parallaxes to tilt and faulty orientation of the photo. • One of the advantages of measuring parallax stereoscopically is increased speed, for once the parallax bar constant is determined, and the parallaxs of all other points are quickly obtained with a single micrometer reading for each point. ØAnother advantage is increased accuracy. An experienced person

HEIGHT MEASUREMENT To use parallax equation. Is generally necessary to compute the flaying height and air base • • Focal –length = 152. 4 Air base = 548 m The elevation of the control point A is = 283 (msl) Parallax of point A is 92. 4 mm What is the flying height above sea level ? H = h + Bf p

Calculatio n H = h + Bf p H = 283+548(152. 4) 92. 4 = 1187 msl Height about sea level = 1187 msl