AED11 AERODIN MICA I Prof GIL O que

AED-11 AERODIN MICA I Prof. GIL

O que é Aerodinâmica? • É a ciência que estuda o movimento do ar em torno de corpos e suas conseqüências físicas; – Sustentação, momento e arrasto – Outros efeitos: termodinâmicos – não estacionários / aeroacústica – não são abordados neste curso.

Fisicamente. . . • Normalmente não vemos um fenômeno aerodinâmico, mas sim sentimos, exceto. . .

Ou quando fazemos questão de ver. . . • Visualização:

Aplica-se a outras áreas. . . • Diferentes da aeronáutica / aeroespacial:

Mas que tem escoamento ao redor de corpos. . .

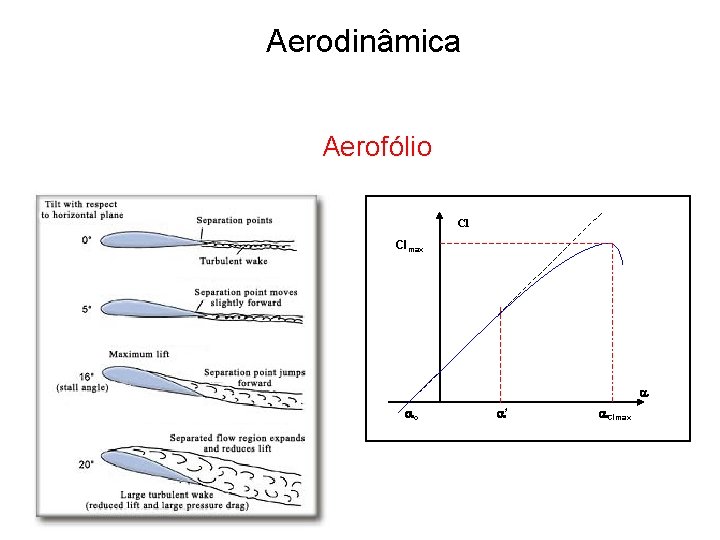
Aerodinâmica Aerofólio Cl Clmax o * Clmax

Aerodinâmica Asa

Aerodinâmica Asa

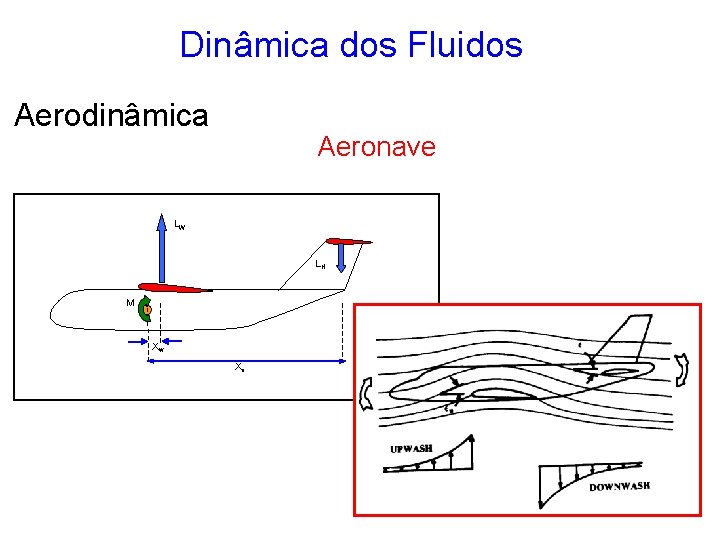
Dinâmica dos Fluidos Aerodinâmica Aeronave LW LH M XW XH

A Atmosfera • Propriedades – Densidade – Viscosidade • Estados – Temperatura – Pressão Dependem da altitude !

Atmosfera Padrão • Estas propriedades são obtidas a partir das relações apresentadas na seção 1. 2 do S&T • Nas nossa aplicações estaremos restritos a primeira camada (até 11 km).

Pressão • A pressão é subdividida em pressão estática e pressão dinâmica: • Pressão estática é a pressão do meio em repouso (ex. atmosférica) • Pressão dinâmica:

Aerodinâmica Básica • O carregamentos aerodinâmicos são apresentados usualmente como:

Propriedades importantes • Do gas (Ar) – Densidade - r – Viscosidade - m (Dependem da temperatura) • Do escoamento – Compressível – Isentrópico (processos termodinâmicos associados reversíveis e adiabáticos)

Sustentação da Aeronave • A asa tem a responsabilidade de garantir o vôo sustentado; • Possui área, forma em planta e perfilagem adequadas para um desempenho desejado; • Perfilagem forma das seções transversais da asa, cujo resultado são os perfis aerodinâmicos, fundamentais no desempenho aerodinâmico da asa

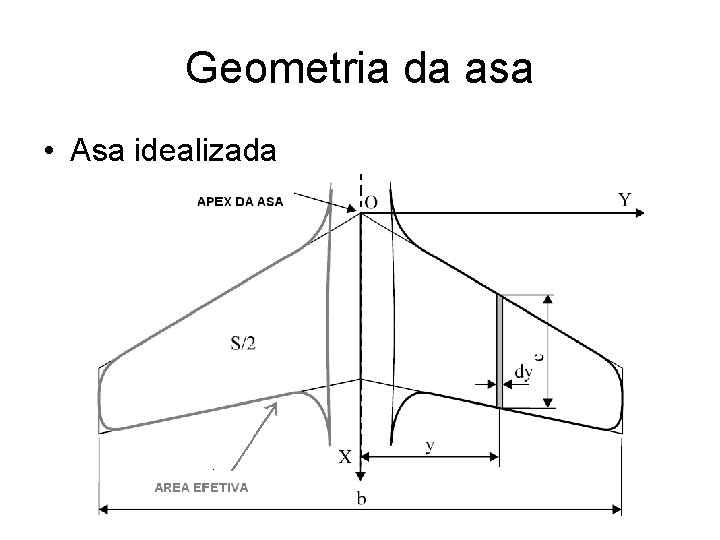
Geometria da asa • Asa idealizada

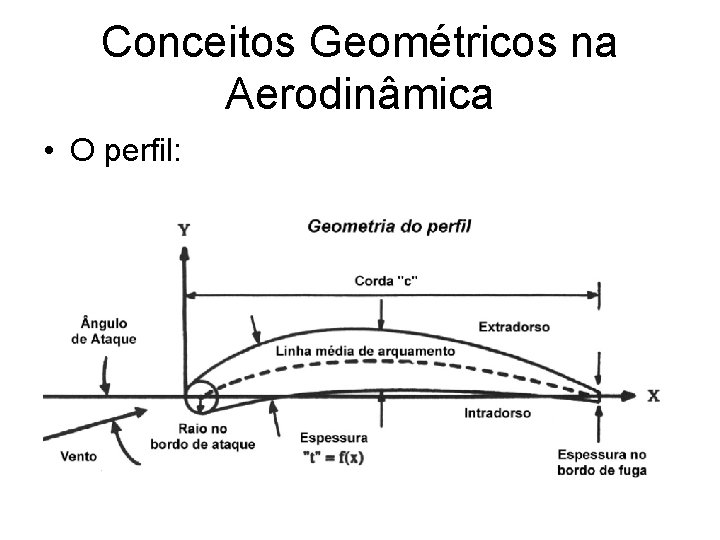
Conceitos Geométricos na Aerodinâmica • O perfil:

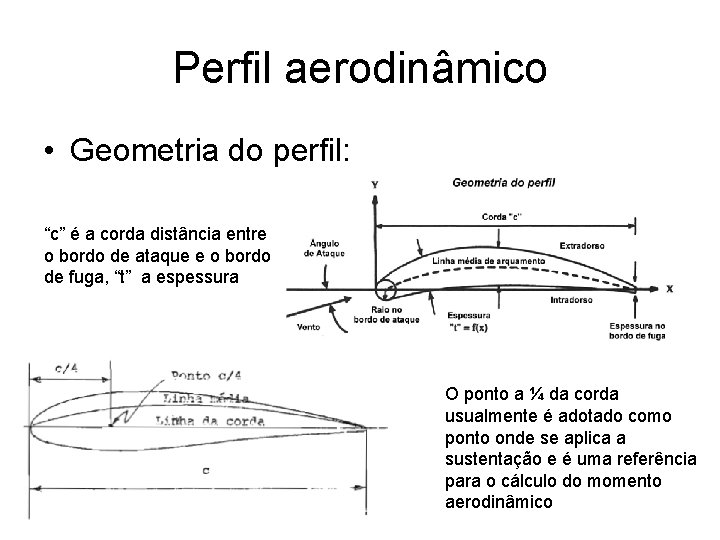
Perfil aerodinâmico • Geometria do perfil: “c” é a corda distância entre o bordo de ataque e o bordo de fuga, “t” a espessura O ponto a ¼ da corda usualmente é adotado como ponto onde se aplica a sustentação e é uma referência para o cálculo do momento aerodinâmico

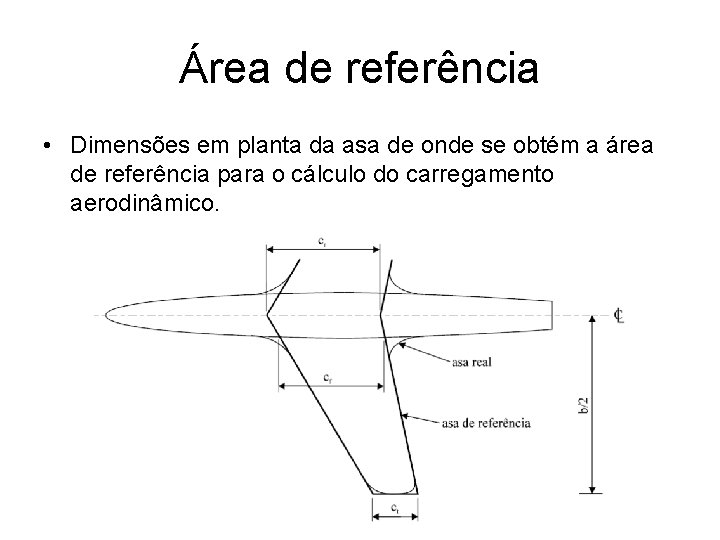
Área de referência • Dimensões em planta da asa de onde se obtém a área de referência para o cálculo do carregamento aerodinâmico.

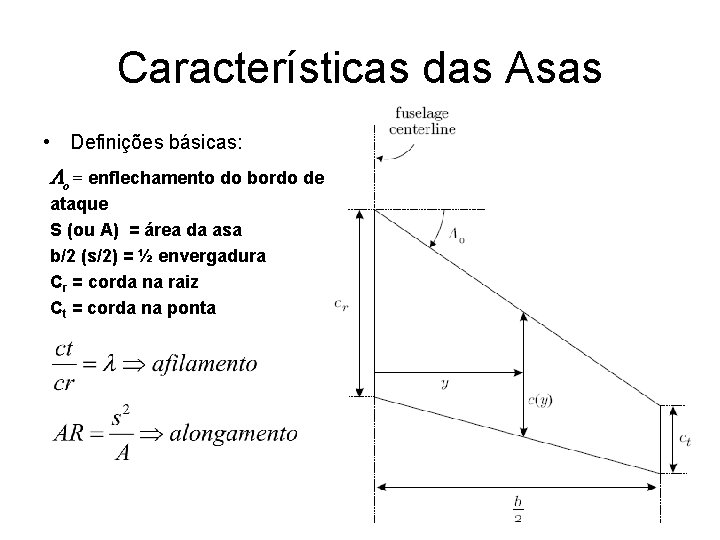
Características das Asas • Definições básicas: Lo = enflechamento do bordo de ataque S (ou A) = área da asa b/2 (s/2) = ½ envergadura Cr = corda na raiz Ct = corda na ponta

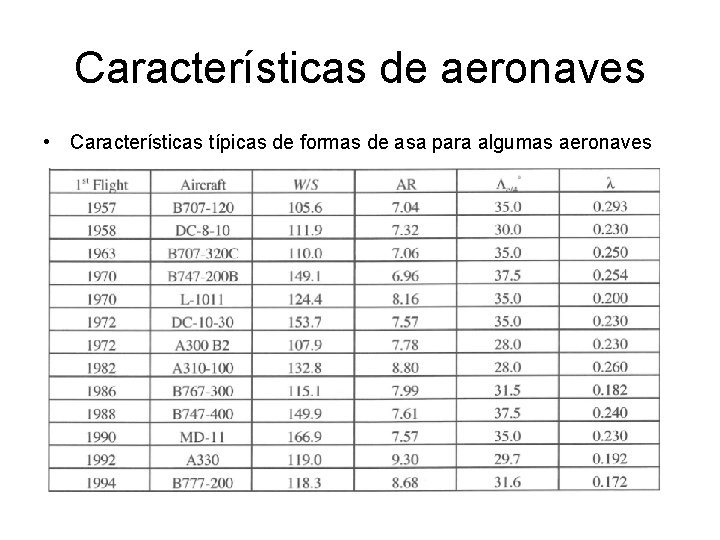
Características de aeronaves • Características típicas de formas de asa para algumas aeronaves

Curvas de sustentação e momento • A sustentação e o momento são função do ângulo de ataque do perfil; • No caso do momento aerodinâmico calculado em torno do centro aerodinâmico, este independerá do ângulo de ataque.

Coeficientes de sustentação e momento e arrasto • Usualmente se emprega em aerodinâmica coeficientes adimensionais que caracterizam a sustentação e momento em função do ângulo de ataque; • E o arrasto também pode ser escrito como um coeficiente que multiplica o ângulo de ataque: • A combinação da sustentação e do arrasto geram esforços aerodinâmicos que podem ser decompostos no sistema do corpo: Força normal, Força de arrasto a – ângulo de ataque

Comportamento Aerodinâmico das Aeronaves • Regras de similaridade: – Mach – Reynolds • Importante em testes: – Ensaios em túnel de vento – Permite relacionar as propriedades medidas em um modelo em escala com as mesmas propriedades associadas ao corpo em tamanho real

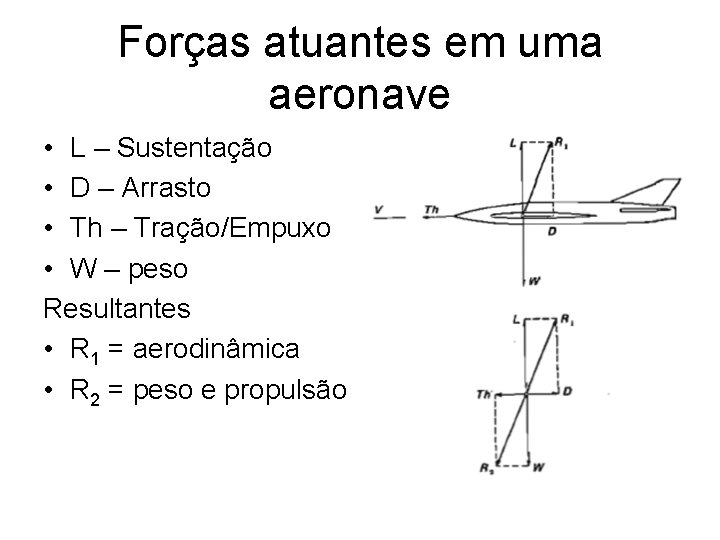
Forças atuantes em uma aeronave • L – Sustentação • D – Arrasto • Th – Tração/Empuxo • W – peso Resultantes • R 1 = aerodinâmica • R 2 = peso e propulsão

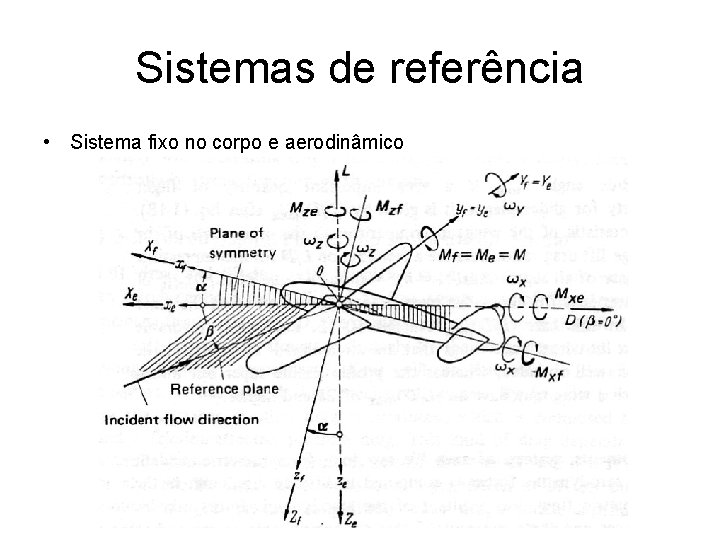
Sistemas de referência • Sistema fixo no corpo e aerodinâmico

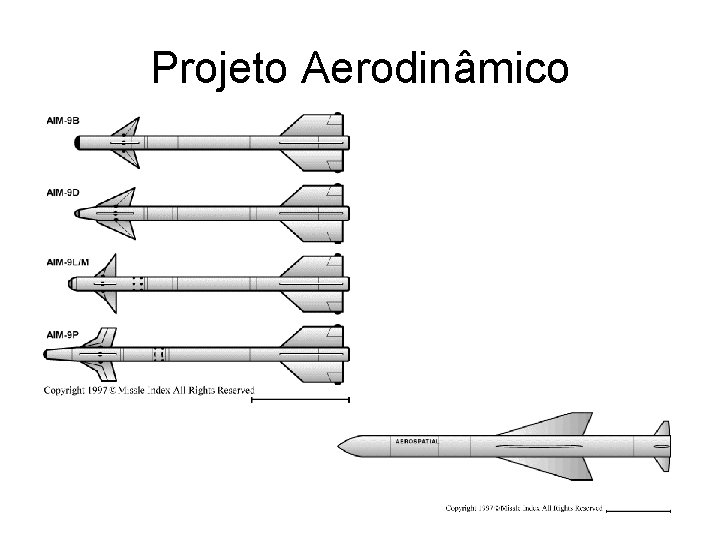
Projeto Aerodinâmico

Desempenho Aerodinâmico

Departamento de Aerodinâmica Metodologia de Ensino Teoria: Prática: - Aulas de Teoria - Séries de exercícios -Testes – Discussão -Prova teoria - Aulas de Laboratório - Laboratórios - Relatórios - Provas Lab. Avaliação da Disciplina: Nota = (Nota Teo. + Nota Lab. ) / 2

Departamento de Aerodinâmica AED 11 – Aerodinâmica Básica Referencias Bibliográficas Karamcheti, K. – “Principles of Ideal Fluid Aerodynamics”, John Wiley & Sons, USA, 1966. Anderson, J. D. , Jr. , Fundamentals of aerodynamics, Mc. Graw Hill, New York, 1985; Schlichting, H. e Truckenbrodt, E. , Aerodynamics of the airplane, Mc. Graw Hill, New York, 1979; Doebelin, E. O. Measurement systems - application and design. Mc. Graw-Hill International Editions, Mechanical Engineering Series, 4 a Ed. , 1990. White, F. M. – “Fluid Mechanics” , Mc. Graw-Hill, USA, 1979. Shames, I. H. – “Mechanics of Fluids”, New York, Mc. Graw-Hill, USA, 1962. Schilichting, H. – “Boudary-layer Theory”, Mc. Graw-Hill, USA, 6 a ed. , 1968.

Departamento de Aerodinâmica AED 11 – Aerodinâmica Básica Conteúdo da Disciplina Estudo do Escoamento Potencial Incompressível: Neste tópico o escoamento potencial será descrito através do potencial de velocidades. As singularidades fonte, vórtice e dipolo serão tratados e o escoamento sobre o cilindro será calculado. Teoria do Perfil Fino: Esta teoria será formulada, deixando claras as suas simplificações e limitações. A mesma será aplicada para: (i) placa plana, (ii) placa arqueada e (ii) placa com flap. As curvas CL x α e Cm x α serão calculadas. Com estes resultados serão introduzidos (e calculados) os conceitos de centros de pressão e aerodinâmico. Perfil Aerodinâmico Real: Com base em resultados experimentais (Lab #1 – perfis) e numéricos, deve-se trabalhar os seguintes conceitos: (i) comparação dos resultados teóricos/ numéricos com os experimentais, (iii) Discutir os efeitos associados a variações de espessura e arqueamento, (iv) Comportamento real de hiper-sustentadores. NOTA: Ênfase deve ser dada a questão do arrasto e da polar de arrasto Teoria da Asa Finita: Teoria da linha sustentadora, conceitos de arrasto induzido e distribuições de sustentação (L) e de coeficiente de sustentação (Cl). Utilizando-se as curvas características de perfil, determinar CL, Cd e Cm de uma asa. Aspectos Práticos sobre Asa Finita: Usando resultados experimentais (Lab # 2 – Asa finita) e numéricos, serão explorados os seguintes conceitos, utilizando-se CL x α, Cd x α e Cm x α, além das distribuições de L e Cl ao longo da envergadura: (i) Efeitos do alongamento, afilamento e enflechamento, (ii) efeitos das torções aerodinâmica e geométrica , (ii) efeito de diedro, (iv) efeito de hiper-sustentadores e de superfícies de controle.

Departamento de Aerodinâmica AED 11 – Aerodinamica Conteúdo da Disciplina Escoamento sobre Fuselagem: Conceitos básicos e método de cálculo simples, complementado com informações práticas sobre o escoamento sobre fuselagem, de maneira que o aluno seja capaz de projetar uma fuselagem. As curvas CL x α, Cd x α e Cm x α, obtidas de forma teórica ou experimental, devem ser exploradas para promover o entendimento do escoamento sobre uma fuselagem. Aeronave Completa: Este tópico integra os conhecimentos adquiridos nos tópicos anteriores e devem ser vistos os seguintes temas: (i) Desenvolvimento das curvas CL x α, e Cl x Cm e CL x Cd. , mostrando as interações que existem entre as diversas partes da aeronave, (ii) Compensação da aeronave, (iii) controle da aeronave- introdução do conceito de derivada de controle. Estudo do Escoamento Potencial Compressível: serão verificadas a influencia da variação do número de Mach nos coeficientes aerodinâmicos de perfis, asas e corpos fuselados (foguetes), para o regime baixo subsônico e supersônico Introdução ao Escoamento Transônico: Descrição do escoamento sobre um aerofólio quando o Mach varia entre 0. 7 até 1. 2. Introdução dos conceitos de Mach crítico, Mach de divergência, buffeting e outros. Introdução ao Escoamento Hipersônico: Nesta parte do curso, é importante fornecer conceitos básico sobre este regime de escoamento, tais como: (i) Validade da hipótese do continuo, (ii) Aquecimento aerodinâmico, (iii) efeito de gás real, (iv) efeito do Mach nos coeficientes aerodinâmicos e (v) Veículos hipersônicos e de reentrada na atmosfera.

Mecânica dos Fluidos • Das equações de Navier-Stokes para a equação potencial linearizada: – – Escoamentos aerodinâmicos são aqueles que ocorrem ao redor de corpos que se movem no tempo, induzindo também um movimento do fluido. Estes movimentos podem ser decompostos como em uma parcela estacionária e uma não estacionaria. A primeira ocorre em torno da forma aerodinâmica do corpo, enquanto que a segunda podem ser consideradas como pequenos movimentos ao redor da condição de estado estacionário, ex. , um aerofólio com a corda alinhada com um escoamento não perturbado, oscilando a pequenos movimentos em arfagem.

O modelo matemático • • O modelo matemático que descreve o escoamento de um fluido contínuo, considerando a viscosidade, compressibilidade e admitindo condução de calor, em um contexto não estacionário é representado pelas as equações de Navier. Stokes. Estas equações representam o comportamento de um fluido a através da derivada substancial das grandezas que caracterizam o escoamento, tais como da massa, velocidade e sua energia. A derivada substancial representa a variação de uma determinada propriedade de um elemento de fluido no tempo simultaneamente com a variação de sua posição no espaço. A derivada substancial é fisicamente diferente da derivada da propriedade no tempo na forma convencional, pois esta última derivada não leva em conta mudança de posição dos elementos de fluido no espaço. As equações de Navier-Stokes são apresentadas a seguir: 35

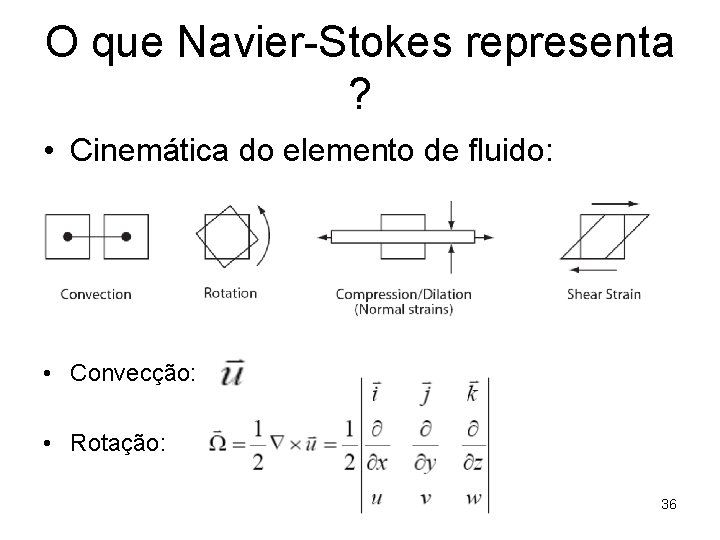
O que Navier-Stokes representa ? • Cinemática do elemento de fluido: • Convecção: • Rotação: 36

Hipótese: Fluido Newtoniano • Tensões viscosas proporcionais ao gradiente de velocidade. 37

Fluido Newtoniano • Tensões viscosas: Um fluido newtoniano é um fluido em que cada componente da velocidade é proporcional ao gradiente de velocidade na direção normal a essa componente. A constante de proporcionalidade é a viscosidade m. 38

Tensões viscosas • Em duas dimensões: 39

O que N-S representa – cont. • Vorticidade: • Tensões no fluido: 40

Outros conceitos: Derivada substancial representa a taxa de variação de uma propriedade do fluido assim que ele se movimenta no tempo e no espaço. 41

O que representa. . . • A divergência quantifica o espalhamento das partículas em um campo vetorial, quantifica a tendência de um campo em divergir convergir. É resultado do produto escalar de um operador gradiente com um campo vetorial • A derivada substancial quantifica a variação de propriedades associadas a partículas de um fluido variando no tempo e no espaço simultaneamente 42

O quer representa. . . • O gradiente transforma um campo escalar em um campo vetorial, representando as taxas de variação de uma determinada grandeza em direções pré-estabelecidas; • O rotacional representa a tendência de um campo rotacional em tono de pontos. Resulta do produto vetorial de um gradiente pelo campo vetorial. 43

Navier-Stokes • Onde é o tensor da tensões viscosas, H é entalpia total, é vetor velocidade, p é a pressão e r é a densidade, e é um fluxo de calor. A derivada: representa a deriva da substancial de uma determinada quantidade. Um fato é ser observado é que tem-se 5 equações para 15 incógnitas, 44

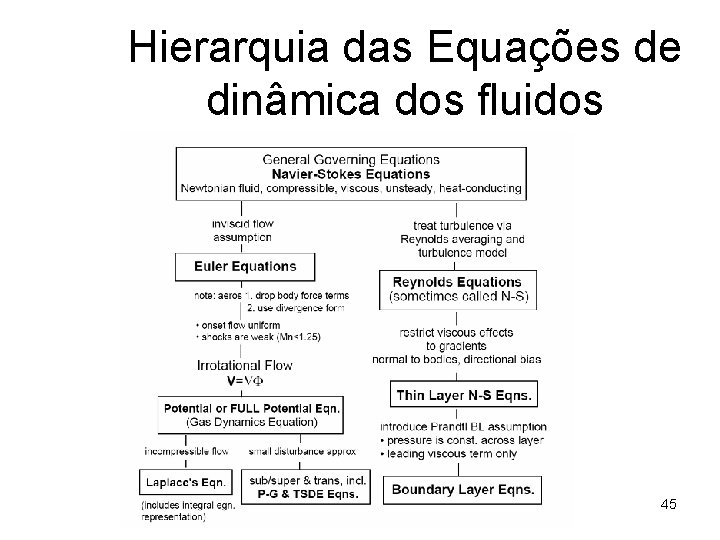
Hierarquia das Equações de dinâmica dos fluidos 45

Aerodinâmica não linear Equações de Navier-Stokes (NS) Direct Numerical Simulation (DNS) Large Eddy Simulation (LES) Reynolds-Averaged Navier-Stokes (RANS) Thin-Layer Approximation 46

Equações de Euler • Prandtl em 1904 concluiu que para número de Reynolds suficientemente grandes, os efeitos importantes relacionados à viscosidade permaneciam confinados em uma camada fina junto ao corpo, ou seja, na camada limite. Esta hipótese é válida para casos onde o comprimento característico dos corpo é bem maior que a espessura desta camada. Desta forma as equações da Navier. Stokes podem ser representadas por uma forma mais simples, onde os efeitos de viscosidade podem ser desconsiderados: • Esta forma é conhecida como as equações de Euler. Os termos de tensões viscosas e de fluxo de calor foram desconsiderados, uma vez que a condutividade térmica é uma função da viscosidade. 47

O modelo matemático Euler 1. Gás perfeito (forças intermoleculares desprezadas) 2. Conservação da massa (continuidade) 3. Conservação da quantidade de movimento 4. Conservação da energia (escoamento adiabático) 5. Forças de campo nulas (gravitacionais, em particular) 6. Forças viscosas não significativas 48

Relações constitutivas: Navier-Stokes • Desta forma faz-se necessário usar relações constitutivas para resolver o problema. Estas relações constitutivas são para a pressão: onde, ei é a energia interna, T a temperatura e Cv a calor específico volume constante. A entalpia é relacionada a estas grandezas por: As tensões viscosas e o fluxo de calor são dados por: 49

Relações constitutivas: Euler • Neste caso são necessárias somente as seguintes relações constitutivas: onde, ei é a energia interna, T a temperatura e Cv a calor específico volume constante. A entalpia é relacionada a estas grandezas por: 50

Modelo Isentrópico • Assumindo a hipótese que o escoamento é isentrópico, isto é reversível e adiabático, pode-se resolver o sistema de equações que representa este tipo de escoamento apenas considerando as conservação da massa e da quantidade de movimento, mas uma relação entre a pressão e a densidade dada pela cadeia isentrópica: • onde p 0 e r 0 são valores de referência para a pressão e densidade respectivamente. Fluido pode ser considerado barotrópico (densidade é função apenas da pressão ou de uma constante), e o sistema de equações agora possui cinco equações escalares e cinco incógnitas, que são as três componentes de velocidade u, v, w, a densidade e a pressão. 51

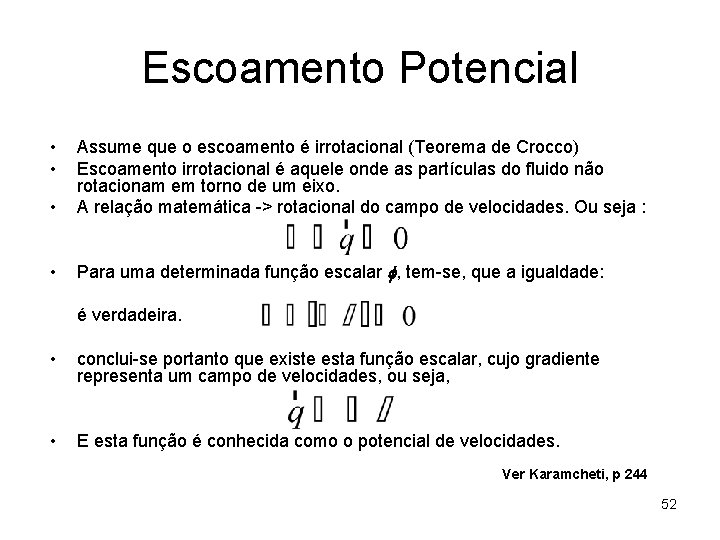
Escoamento Potencial • • • Assume que o escoamento é irrotacional (Teorema de Crocco) Escoamento irrotacional é aquele onde as partículas do fluido não rotacionam em torno de um eixo. A relação matemática -> rotacional do campo de velocidades. Ou seja : • Para uma determinada função escalar f, tem-se, que a igualdade: é verdadeira. • conclui-se portanto que existe esta função escalar, cujo gradiente representa um campo de velocidades, ou seja, • E esta função é conhecida como o potencial de velocidades. Ver Karamcheti, p 244 52

Potencial de velocidades • O potencial de velocidades f é uma função das coordenadas espaciais, onde cada uma das componentes de velocidade do vetor velocidade total são as derivadas do potencial em cada uma das direções do sistemas de coordenadas: • Com a definição do potencial de velocidade pode-se reduzir ainda mais o problema de cinco equações a cinco incógnitas para três equações e três incógnitas. 53

Passos subsequentes: • Redução do número de incógnitas com a introdução do potencial: • Dedução da equação de Bernoulli , ou Equação de Kelvin; 54

Equação de Kelvin I • • Conhecida também como Bernoulli não estacionária. Vamos derivar este equação pois ele será empregada na dedução de uma equação função do potencial de velocidades. Momentum na forma vetorial: substituindo : temos: 55

Equação de Kelvin II • Uma vez que: e como o escoamento é irrotacional, temos: portanto, 56

Equação de Kelvin III • • O lado direito da não está expresso em termos de um gradiente puro do potencial Usamos o Teorema de Liebnitz: (Ver Hildebrandt) • Sabendo que: Portanto, aplicando o teorema temos: O gradiente da função densidade é uma função explícita somente da pressão, isto é independe de x, y e z, portanto o seu gradiente será nulo. 57

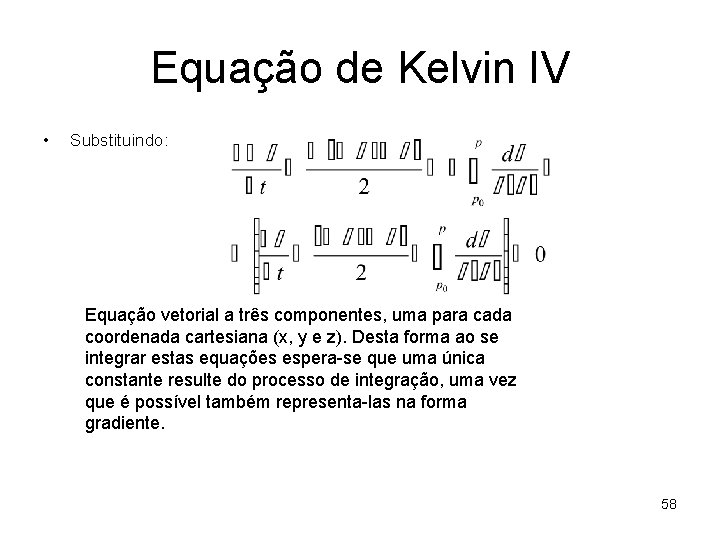
Equação de Kelvin IV • Substituindo: Equação vetorial a três componentes, uma para cada coordenada cartesiana (x, y e z). Desta forma ao se integrar estas equações espera-se que uma única constante resulte do processo de integração, uma vez que é possível também representa-las na forma gradiente. 58

Equação de Kelvin V • • • No entanto, a única variável que é comum às três equações é o tempo, ou seja a constante resultante deverá ser pelo menos uma função desta variável. O resultado da integração da Equação de Kelvin, que não deixa de ser a versão não estacionária da equação de Bernoulli: Onde F(t) é a constante de integração. Para avaliar o seu valor, toma-se como referência as condições de contorno de escoamento não perturbado dadas por: 59

Equação de Kelvin VI • Com as condições de contorno: • ou seja, nota-se que a constante de integração não é só independente do espaço, mas também independe do tempo; O valor prático da equação de Kelvin é que ele permite relacionar o potencial à pressão, quando se considera a relação isentrópica; Todavia ainda sim é necessário mais uma relação para se obter uma equação única em termos do potencial de velocidade. • • 60

Equação de Kelvin VII • O valor prático desta equação é a sua relação entre o potencial à pressão, considerando como hipótese um escoamento barotrópico. 61

Equação como função somente do potencial • Vamos fazer novamente uso da equação da continuidade, • aliada a condição que o escoamento é isentrópico • e que a velocidade do som é dada por: 62

Equação do Potencial Completo I • Para se obter uma equação única em termos do potencial de velocidade, vamos recorrer novamente à equação da continuidade: que pode ser reescrita como: {objetivo} estamos usando a relação isentrópica mais a relação para a velocidade do som para obtê-lo como função do potencial de velocidade. 63

Equação do Potencial Completo II • Multiplicando o primeiro termo pela velocidade do som, tem-se: derivando a equação de Kelvin com relação ao tempo tem-se: 64

Equação do Potencial Completo III • Usando novamente a regra de Liebnitz, tem-se: Substituindo na Equação de Kelvin derivada no tempo: e assim temos o primeiro termo da equação da continuidade escrito como uma função do potencial e da velocidade do som. 65

Equação do Potencial Completo IV • O segundo termo da equação de Kelvin pode ser representado em termos do potencial a partir da forma gradiente desta equação: Sabendo que: Temos: 66

Equação do Potencial Completo V • Finalmente, de pois de fazer um produto escalar entre a relação anterior e o gradiente do potencial de velocidade temos: • A equação do potencial completo é finalmente obtida substituindo a relação acima, mais a seguinte relação: 67

Equação do Potencial Completo VI • . . . na equação da continuidade: para se obter: Equação do Potencial Completo 68

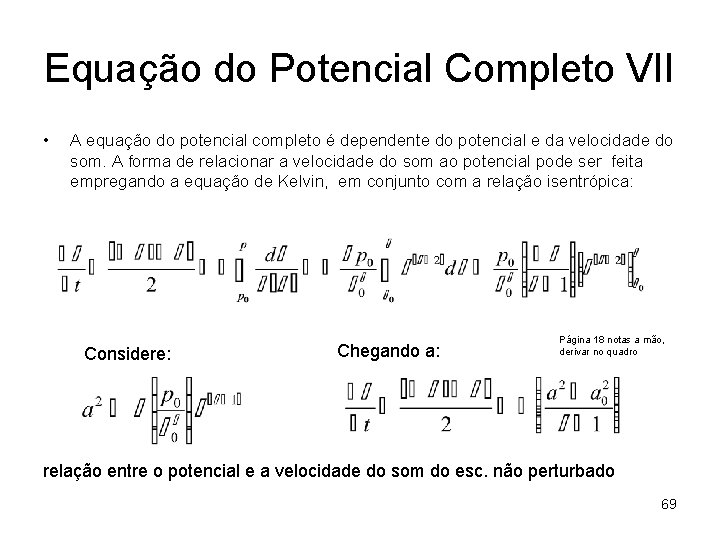
Equação do Potencial Completo VII • A equação do potencial completo é dependente do potencial e da velocidade do som. A forma de relacionar a velocidade do som ao potencial pode ser feita empregando a equação de Kelvin, em conjunto com a relação isentrópica: Considere: Chegando a: Página 18 notas a mão, derivar no quadro relação entre o potencial e a velocidade do som do esc. não perturbado 69

Equação do Potencial Completo VIII • Equação de Kelvin modificada: • Com esta relação pode-se escrever a equação do potencial completo como uma função exclusivamente do potencial; • É um processo complexo, e no momento não é necessário, uma vez que o próximo passo será a linearização da Equação do Potencial Completo. 70

Equação do Potencial Completo IX • • A equação do potencial completo, na forma apresentada anteriormente é não linear, ou seja poderia representar fenômenos não lineares; Entretanto, o potencial é uma função harmônica, ou seja tem derivadas contínuas dentro de um domínio; Porém uma não linearidade tal como o choque pode ser considerado uma descontinuidade no domínio, e a priori a teoria do potencial aerodinâmico falharia. Este assunto ainda é motivo de discussão; pode-se usar o potencial para modelar um problema transônico, onde eu tenho a presença de descontinuidades tal como as ondas de choque? 71