ADVENTURES IN EXPLODING DOTS Exploration 7 All Bases

ADVENTURES IN EXPLODING DOTS: Exploration 7 All Bases, All at Once: Polynomials Discovering that all the work of K-6 arithmetic is essentially high-school polynomial algebra

Teacher Notes PART 1: A famous mystery about prime numbers PART 2: Division in base 10: A quick recap PART 3: Division in any base PART 4: A problem! PART 5: Resolution PART 6: The opening mystery Example dialogue appears in blue. This Exploration could be conducted as a single, fast-paced lesson or taken slowly over a several class periods.

Teacher Notes PART 1: A Famous Mystery about Prime Numbers Here’s a You. Tube video of James conducting this first section on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/Ox 48 m 0 p 3 Eg 4 [7: 16 minutes]

Teacher Notes Here are the doubling numbers, that is, the powers of two.

Teacher Notes

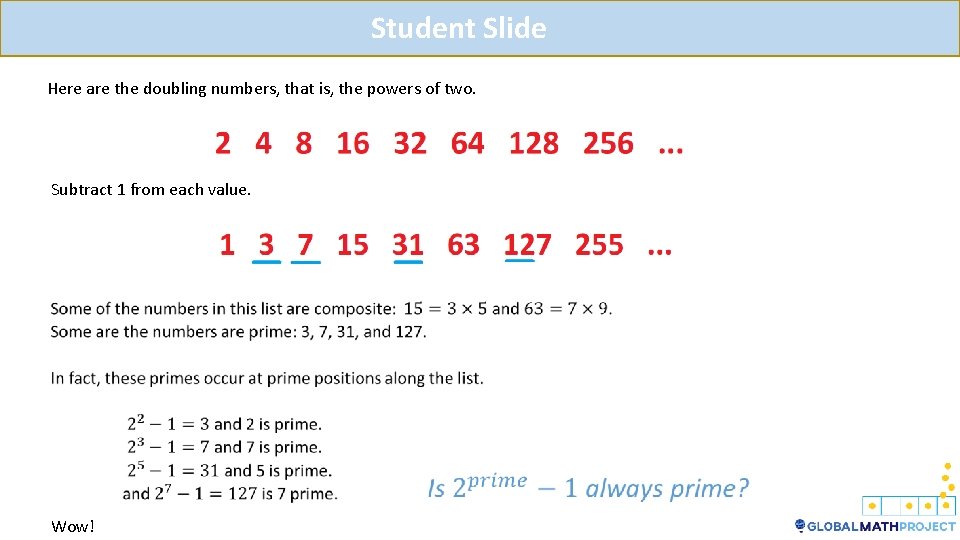
Student Slide Here are the doubling numbers, that is, the powers of two. Subtract 1 from each value. Wow!

Student Slide

Teacher Notes PART 2: Division in Base 10: A Quick Recap Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/Ir. Zoz. Ztc. Qt 0 [2: 01 minutes]

Teacher Notes We drew a picture of the number 12. It appears as one dot next to two dots, but it is really twelve dots in the rightmost box. Next we identified groups of 12 in the picture of 276. And there are plenty of them: two at the tens level and three at the ones level. (Remember, the twelve dots appear in the right part of each loop: an explosion must have “spilled” one dot over to the left. )

Teacher Notes

Student Slide

Teacher Notes PART 3: Division in any Base Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/p. TM 9 tn. Pgjdo [15: 50 minutes]

Teacher Notes Okay. Let’s now jump from grade-school arithmetic straight to advanced high school algebra. Whoa! But here’s the thing: there is nothing to it. We’ve already done all the work. The only thing we have to realize is that there is nothing special about a 1 10 machine. We could do all of grade school arithmetic in a 1 2 machine if we wanted to, or a 1 5 machine, or even a 1 37 machine. The math doesn’t care in which machine we conduct it. It is only us humans with a predilection for the number ten that draws us to the 1 10 machine. So, let’s now be bold and do our work in all possible machines, all at once! Sounds crazy. But it is surprisingly straightforward.

Teacher Notes

Teacher Notes Whoa! STEP 1: Deep breath! This does look scary, so take a deep breath. STEP 2: Do Something!

Teacher Notes

Teacher Notes We’ve just done a high school algebra problem as though it is a grade school arithmetic problem. We have identical pictures!

Teacher Notes

Student Slide

Teacher Notes PART 4: A Problem! Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/Tl. NT 7 z. Zi. O 5 c [1: 47 minutes]

Teacher Notes

Student Slide

Teacher Notes PART 5: Resolution Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/EGy. Uv 4 VP 5 x 4 [8: 58 minutes]

Teacher Notes

Teacher Notes The situation seems hopeless at present. But I have a piece of advice for you, a general life lesson in fact. It’s this: IF THERE IS SOMETHING IN LIFE YOU WANT … MAKE IT HAPPEN! (And deal with the consequences. ) Right now, is there anything in life we want?

Teacher Notes Brilliant! We now have one copy of what we’re looking for. But there is still the question: Is this brilliant idea actually helpful? Hmm.

Teacher Notes This is all well and good, but are we now stuck? Maybe this brilliant idea really just isn’t helpful.

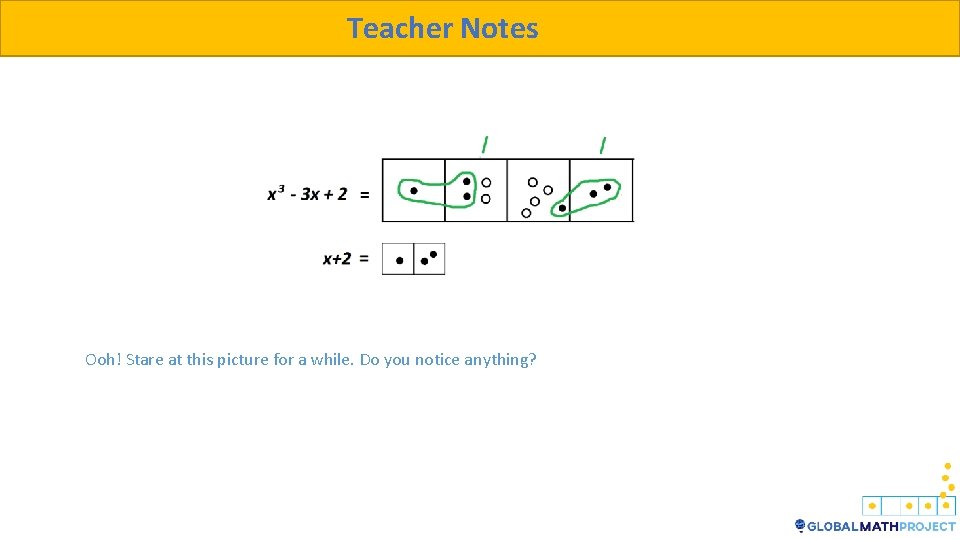
Teacher Notes Ooh! Stare at this picture for a while. Do you notice anything?

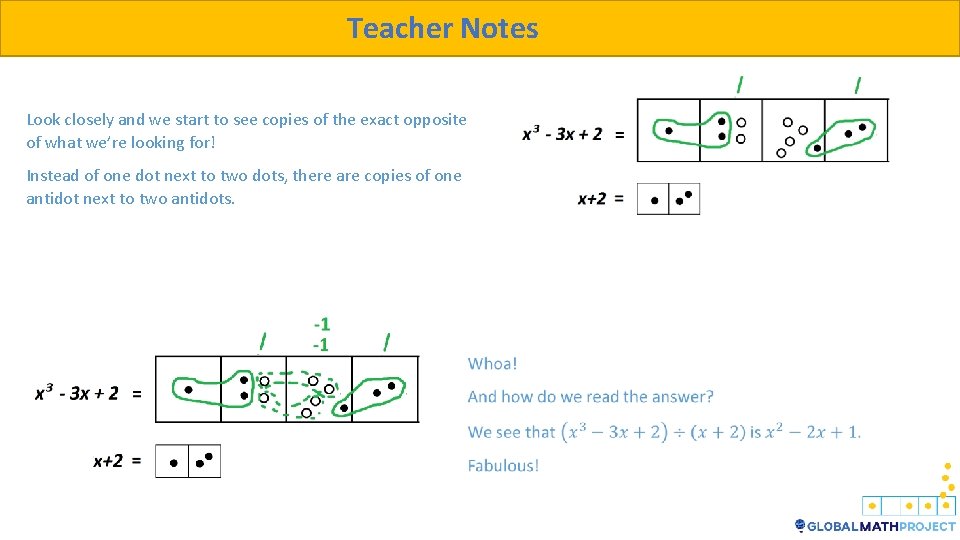
Teacher Notes Look closely and we start to see copies of the exact opposite of what we’re looking for! Instead of one dot next to two dots, there are copies of one antidot next to two antidots.

Teacher Notes So actually, we can do all polynomial division problems with this dots and boxes method, even ones with negative numbers.

Teacher Notes

Student Slide

Teacher Notes PART 5: The Opening Mystery Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/Rs 980 gi 0 t. O 4 [8: 45 minutes]

Teacher Notes

Teacher Notes Here are the PRACTICE PROBLEMS in the take-home handout.