ADVENTURES IN EXPLODING DOTS Exploration 6 Fractions as

ADVENTURES IN EXPLODING DOTS: Exploration 6 Fractions as Decimals Making sense of decimals and writing fractions as decimals (and a weird way to divide by 9).

Teacher Notes PART 1: Discovering Decimals PART 2: Fractions as Sharing PART 3: Fractions as Decimals EXTRA: Divisibility by Nine—Again! Example dialogue appears in blue. This Exploration could be conducted as a single, fast-paced lesson or taken slowly over a several class periods.

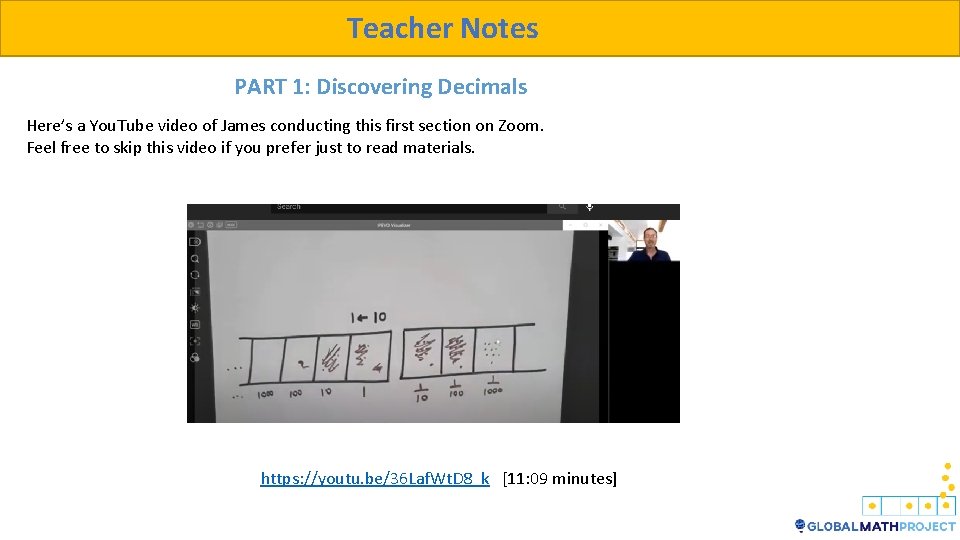
Teacher Notes PART 1: Discovering Decimals Here’s a You. Tube video of James conducting this first section on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/36 Laf. Wt. D 8_k [11: 09 minutes]

Teacher Notes All our machines, so far, have had boxes going to the left as far as we please. But that seems awfully lopsided! Why can’t we have boxes going infinitely far to the right as well? Mathematicians like symmetry and so let’s follow suit and now make all our machines symmetrical. Let’s have boxes going to the left and to the right. But the challenge now is to figure out what those boxes to the right mean.

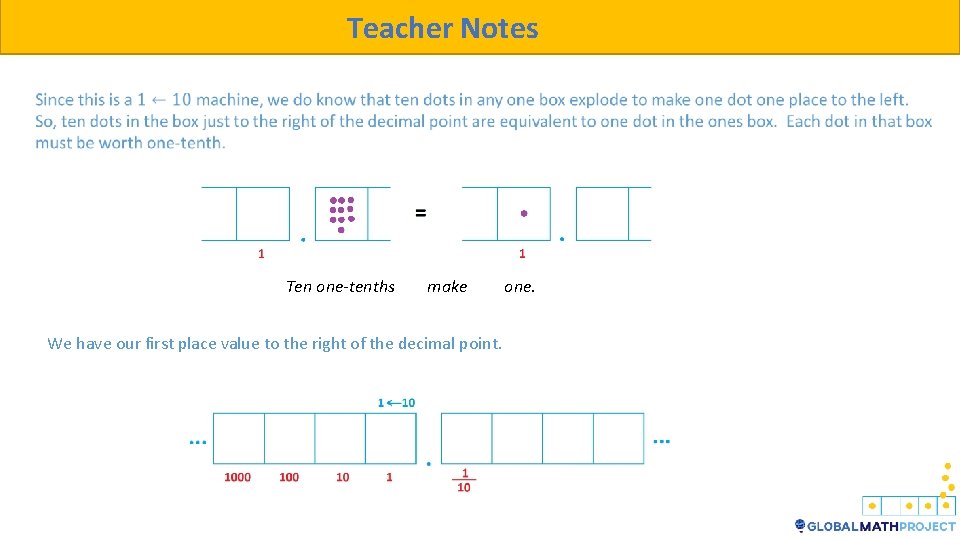
Teacher Notes So, what does it mean to have dots in the right boxes? What are the values of dots in those boxes?

Teacher Notes Ten one-tenths make We have our first place value to the right of the decimal point. one.

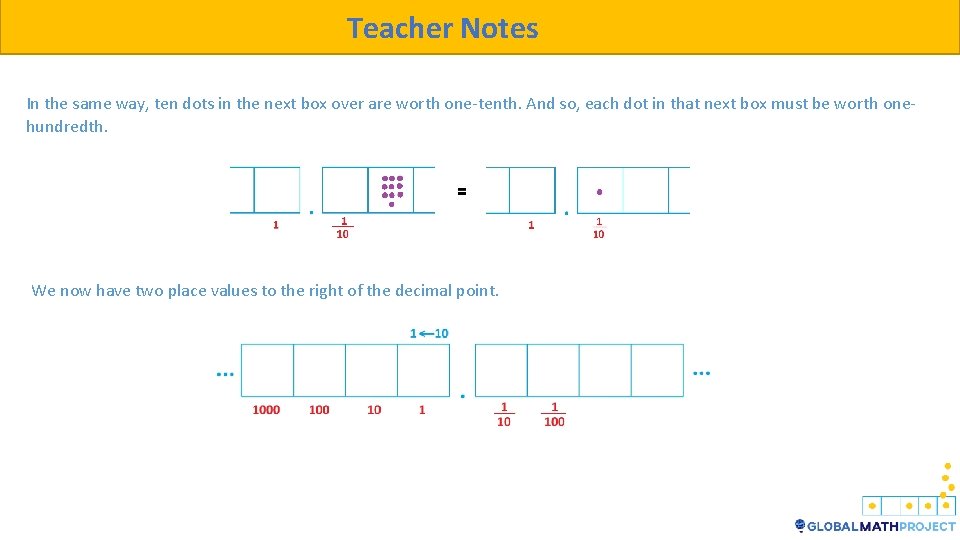
Teacher Notes In the same way, ten dots in the next box over are worth one-tenth. And so, each dot in that next box must be worth onehundredth. We now have two place values to the right of the decimal point.

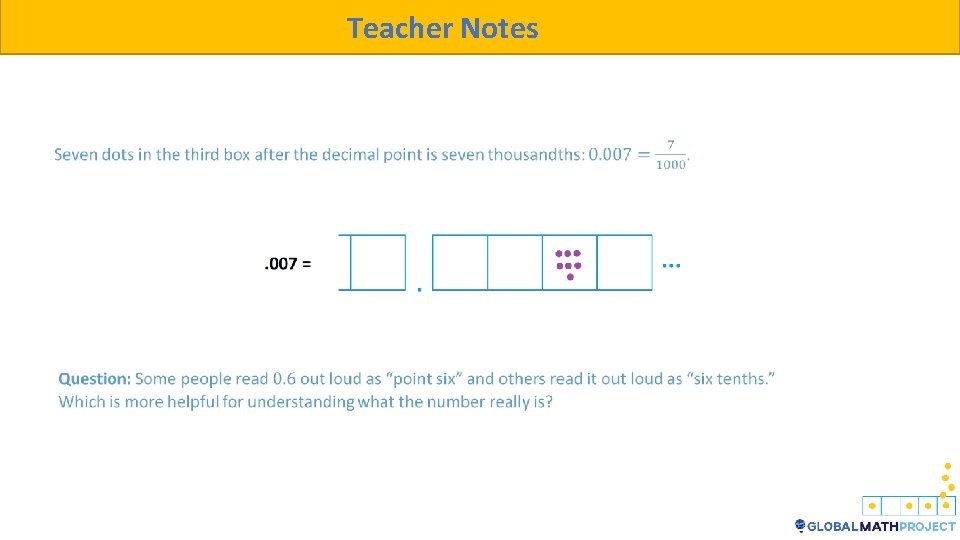
Teacher Notes And ten one-thousandths make a hundredth, and ten-thousandths make a thousandth, and so on. We see that the boxes to the left of the decimal point represent place values as given by the powers of ten, and the boxes to the right of the decimal point represent place values given by the reciprocals of the powers of ten. We have just discovered decimals!

Teacher Notes

Teacher Notes

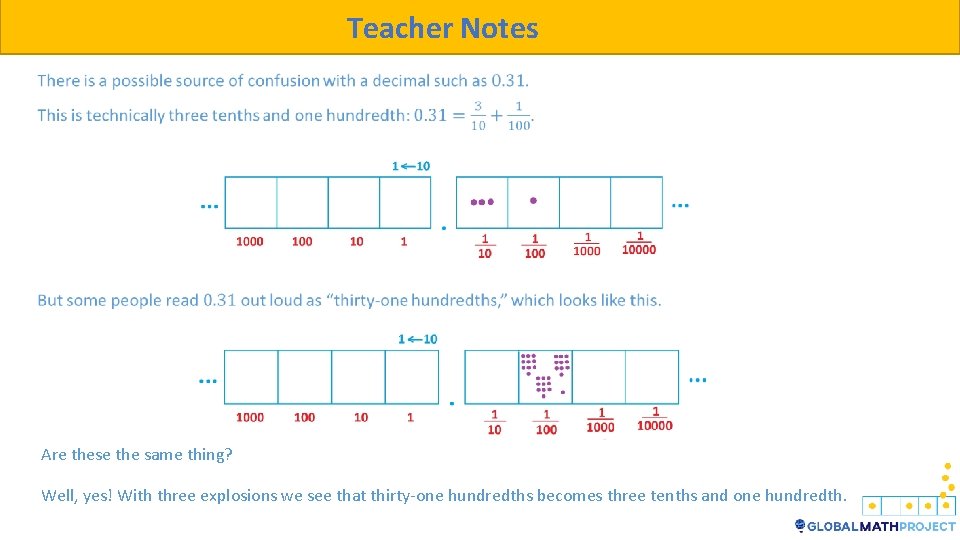
Teacher Notes Are these the same thing? Well, yes! With three explosions we see that thirty-one hundredths becomes three tenths and one hundredth.

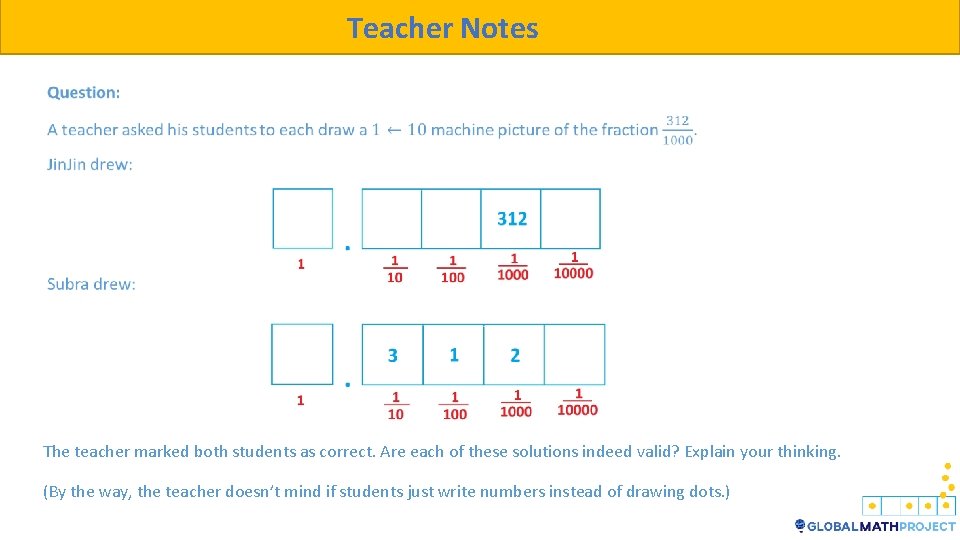
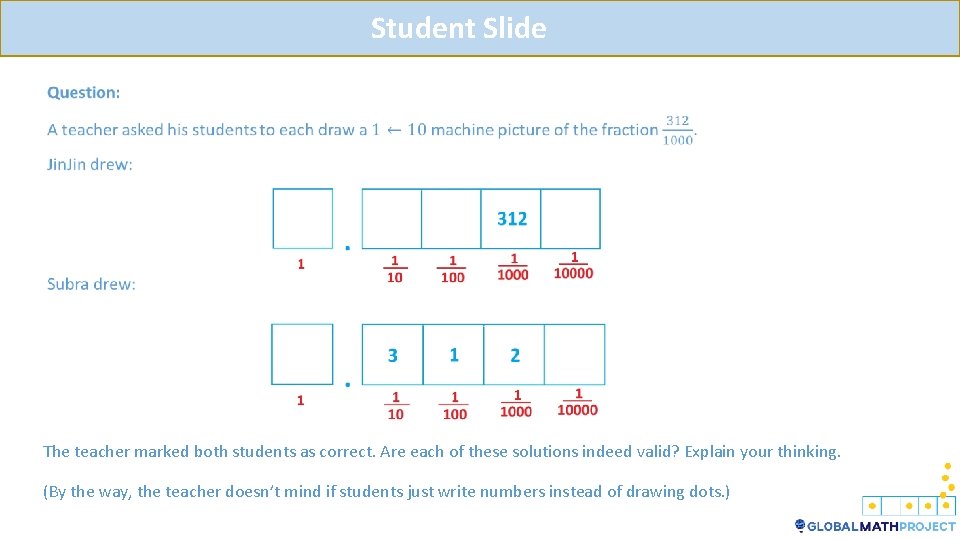
Teacher Notes The teacher marked both students as correct. Are each of these solutions indeed valid? Explain your thinking. (By the way, the teacher doesn’t mind if students just write numbers instead of drawing dots. )

Teacher Notes It’s absolutely valid! We have this picture. Perform some explosions to convert this one society expects. (28. 211)

Teacher Notes

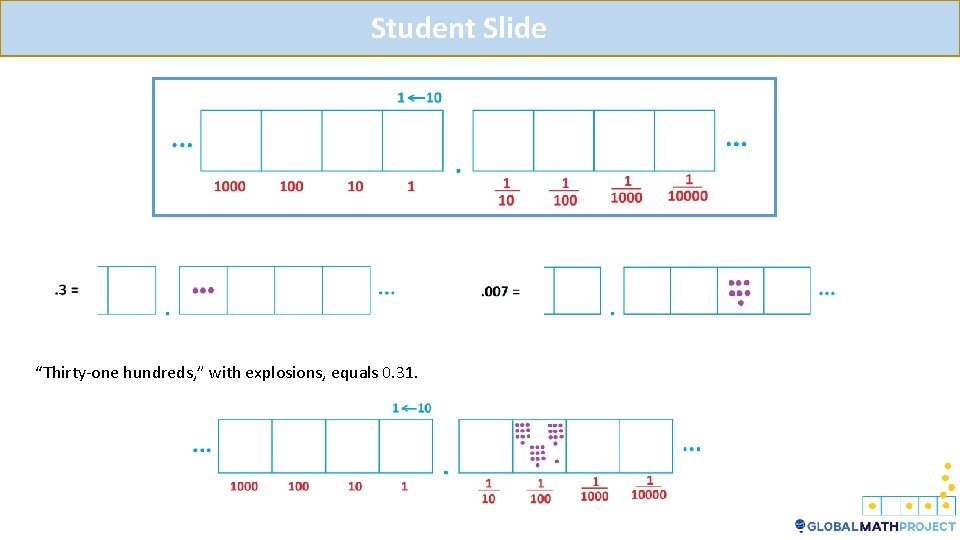
Student Slide “Thirty-one hundreds, ” with explosions, equals 0. 31.

Student Slide The teacher marked both students as correct. Are each of these solutions indeed valid? Explain your thinking. (By the way, the teacher doesn’t mind if students just write numbers instead of drawing dots. )

Student Slide

Student Slide

Teacher Notes PART 2: Fractions as Sharing Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/ug. CA 5 Oi. Wzn. U [3: 35 minutes]

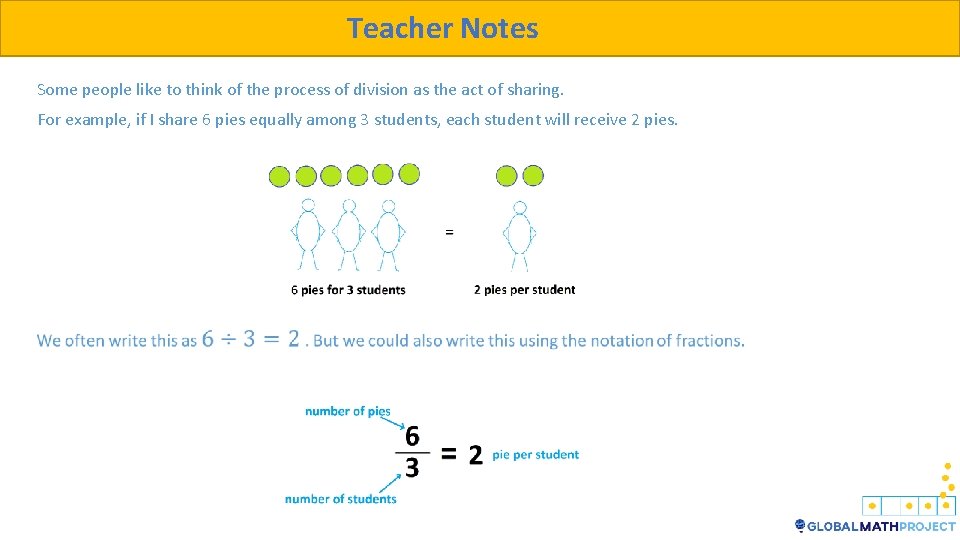
Teacher Notes Some people like to think of the process of division as the act of sharing. For example, if I share 6 pies equally among 3 students, each student will receive 2 pies.

Teacher Notes One pie divided into two equal parts really does give what we call “half a pie” for each student.

Teacher Notes

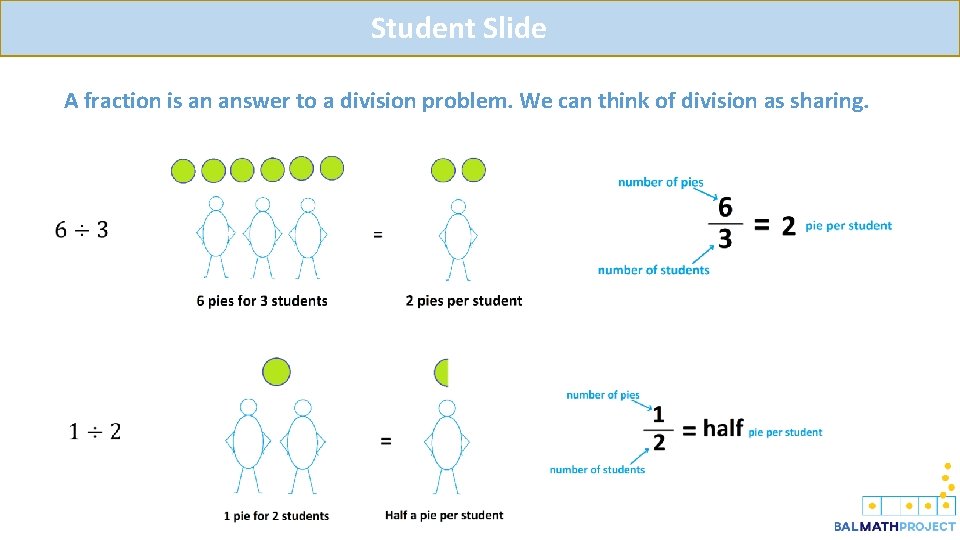
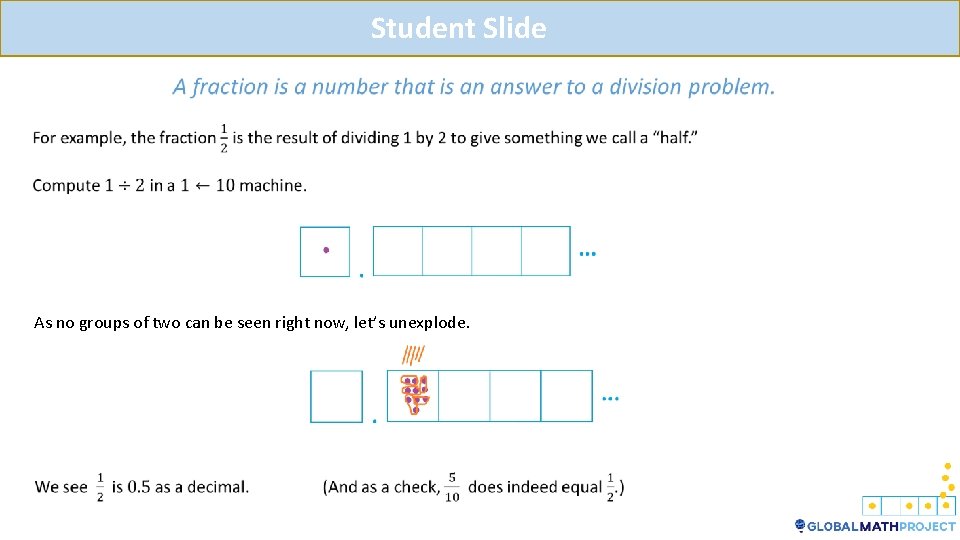
Student Slide A fraction is an answer to a division problem. We can think of division as sharing.

Student Slide

Teacher Notes PART 3: Fractions as Decimals Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/Y 6 n 1 f. T_Xoj. Q [9: 15 minutes]

Teacher Notes No groups of two can be seen right now, so, let’s unexplode. Then we see five groups of two at the tenths level.

Teacher Notes

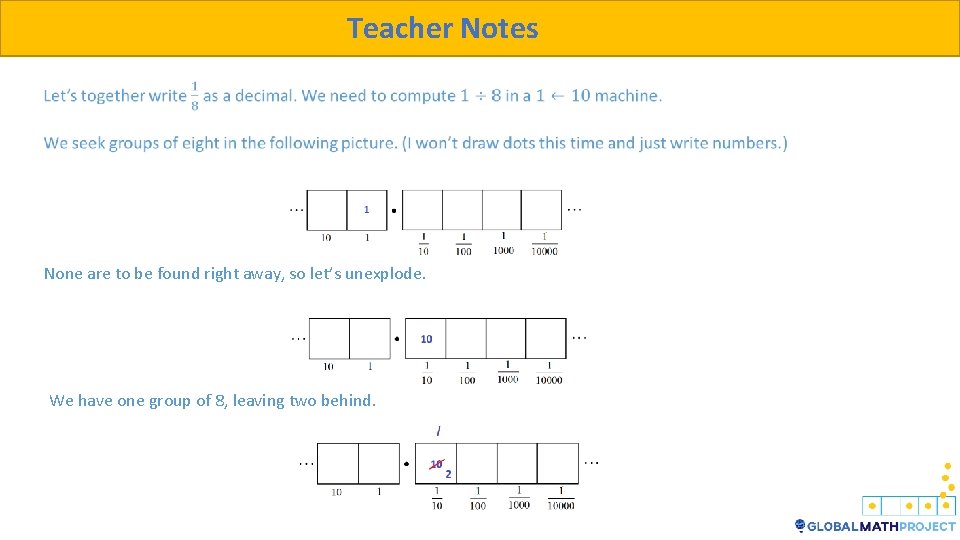
Teacher Notes None are to be found right away, so let’s unexplode. We have one group of 8, leaving two behind.

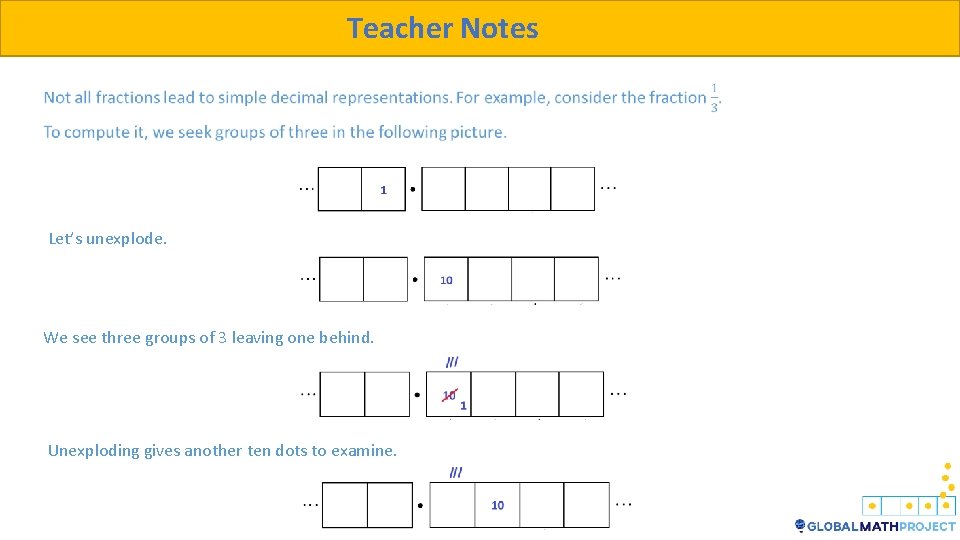
Teacher Notes Let’s unexplode. We see three groups of 3 leaving one behind. Unexploding gives another ten dots to examine.

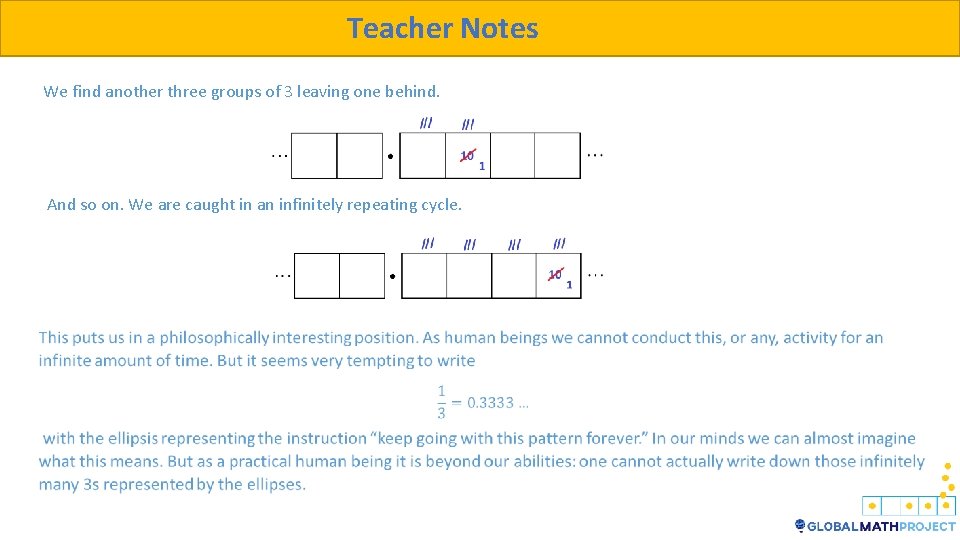
Teacher Notes We find another three groups of 3 leaving one behind. And so on. We are caught in an infinitely repeating cycle.

Teacher Notes Nonetheless, many people choose not to contemplate what an infinite statement like this means and just carry on and say that some decimals are infinitely long and not worry about it. The fraction is one of those fractions whose decimal expansion goes on forever.

Teacher Notes ASIDE Some students might enjoy this aside. (It can be a lesson in its own right!)

Student Slide As no groups of two can be seen right now, let’s unexplode.

Student Slide

Student Slide

Teacher Notes EXTRA: Divisibility by Nine—Again! This section is completely optional and best suited for later-grade students. Here’s a You. Tube video of James conducting this part of the lesson on Zoom. Feel free to skip this video if you prefer just to read materials. https: //youtu. be/guvw 5 pd 0 DW 0 [11: 58 minutes]

Teacher Notes This section is completely optional and best suited for later-grade students. Here’s a strange way to divide a number by 9. We’ll illustrate it with a specific example. To divide 312 by 9, write out the partial sums of its digits, computed from left to right

Teacher Notes and a remainder of 16 really corresponds to one extra group of 9 and a remainder of 7. So, we actually have

Teacher Notes Practice: Test this algorithm with more examples. Of course, the real question here is: Why does this curious algorithm work?

Teacher Notes

Teacher Notes

Teacher Notes Do the explosions. Do you see that this picture results?

Teacher Notes

Student Slide Here’s a strange way to divide a number by 9. We’ll illustrate it with a specific example. To divide 312 by 9, write out the partial sums of its digits, computed from left to right

Student Slide and a remainder of 16 really corresponds to one extra group of 9 and a remainder of 7. So, we actually have Practice: Test this algorithm with more examples.

Student Slide

Student Slide Does this picture make sense to you? Can you now explain the curious division algorithm?

Student Slide

Teacher Notes Here are the PRACTICE PROBLEMS in the take-home handout.

Teacher Notes