Advantages of Using CMOS Compact shared diffusion regions









- Slides: 81

Advantages of Using CMOS • Compact (shared diffusion regions) • Very low static power dissipation • High noise margin (nearly ideal inverter voltage transfer characteristic) • Very well modeled and characterized • Mechanically robust • Lends itself very well to high integration levels • “Analog” CMOS process usually includes non-salicided poly layer for linear resistors. • Si. Ge Bi. CMOS is very useful but is a generation behind currently available standard CMOS EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 1

Transistor f. T Calculation VDD ig vgs id f. T is the frequency at which becomes 1. Cgs VGS f. T gives a fundamental speed measure of a technology. 0. 25 µm CMOS: f. T ~ 23 GHz (VDD = 2. 5 V) 0. 18 µm CMOS: f. T ~ 57 GHz (VDD = 1. 8 V) EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 2

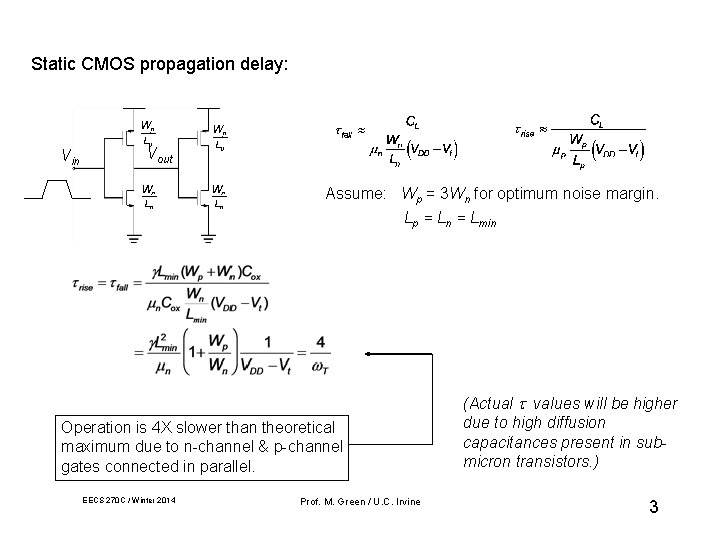
Static CMOS propagation delay: Vin Vout Assume: Wp = 3 Wn for optimum noise margin. Lp = Ln = Lmin Operation is 4 X slower than theoretical maximum due to n-channel & p-channel gates connected in parallel. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine (Actual values will be higher due to high diffusion capacitances present in submicron transistors. ) 3

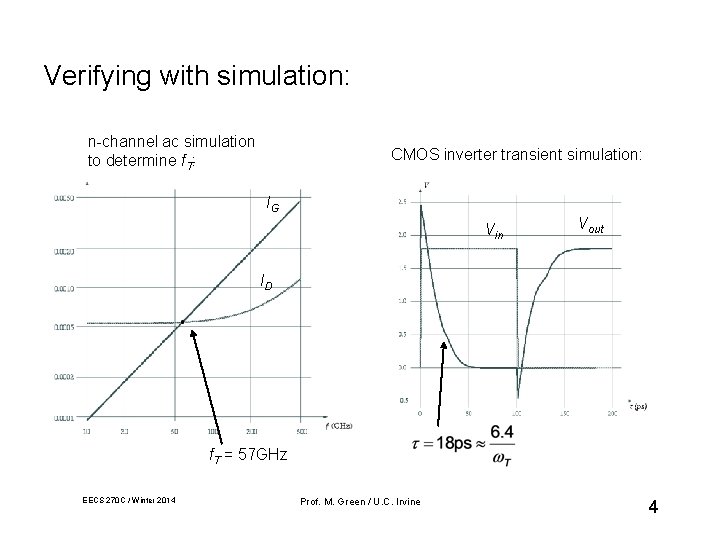
Verifying with simulation: n-channel ac simulation to determine f. T: CMOS inverter transient simulation: IG Vin Vout ID f. T = 57 GHz EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 4

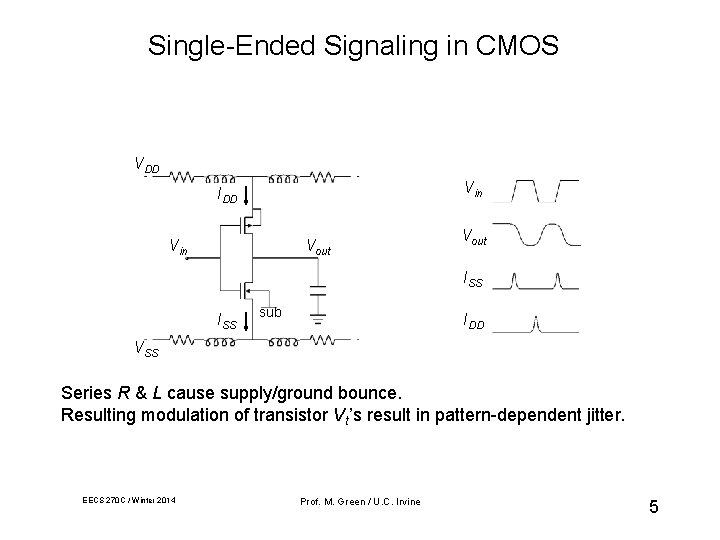
Single-Ended Signaling in CMOS VDD Vin IDD Vin Vout ISS sub IDD VSS Series R & L cause supply/ground bounce. Resulting modulation of transistor Vt’s result in pattern-dependent jitter. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 5

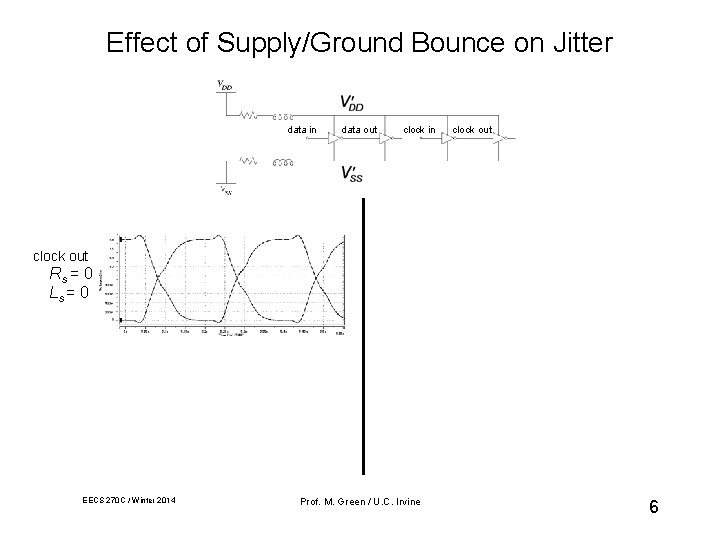
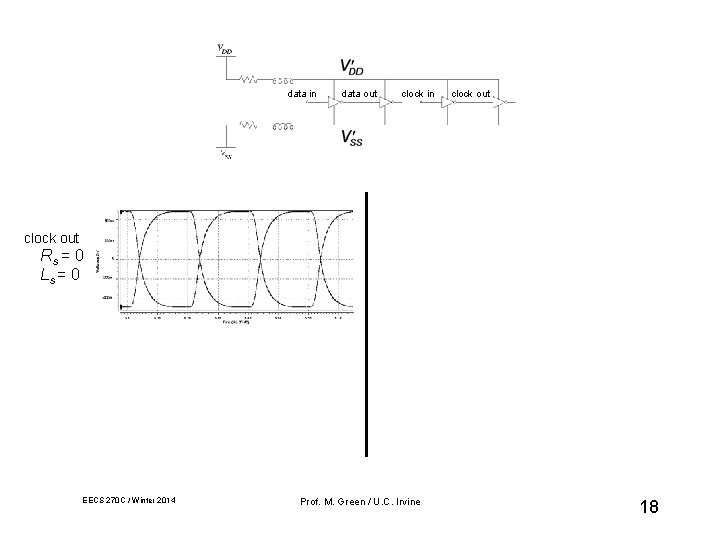
Effect of Supply/Ground Bounce on Jitter data in data out clock in clock out Rs = 5 Ls = 5 n. H clock out Rs = 0 Ls = 0 clock out Rs = 5 Ls = 5 n. H EECS 270 C / Winter 2014 data out Prof. M. Green / U. C. Irvine 6

Summary of CMOS Gate Performance Advantages of static CMOS gates: 1. 2. 3. Simple & straightforward design. Robust operation. Nearly zero static power dissipation. Disdvantages of static CMOS gates: 1. 2. 3. Full speed of transistors not exploited due to n-channel & pchannel gate in parallel at load. Single-ended operation causes current spikes leading to VDD/VSS bounce. Single-ended operation also highly sensitive to VDD/VSS bounce leading to jitter. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 7

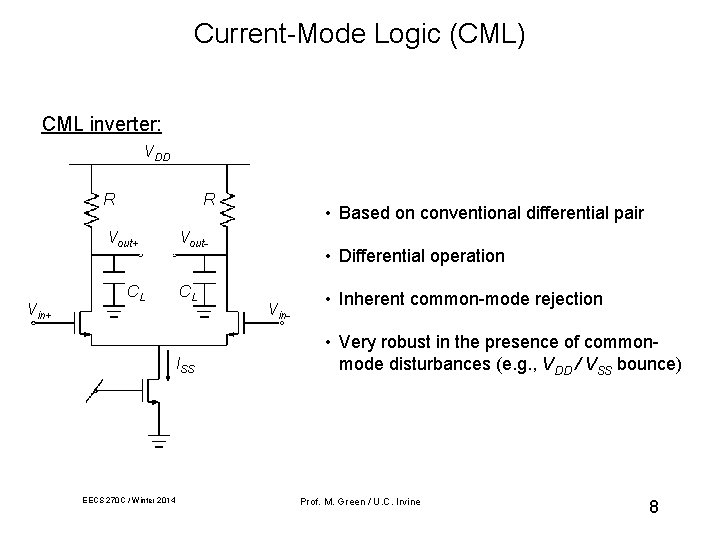
Current-Mode Logic (CML) CML inverter: VDD R R Vout+ Vin+ CL Vout. CL ISS EECS 270 C / Winter 2014 • Based on conventional differential pair • Differential operation Vin- • Inherent common-mode rejection • Very robust in the presence of commonmode disturbances (e. g. , VDD / VSS bounce) Prof. M. Green / U. C. Irvine 8

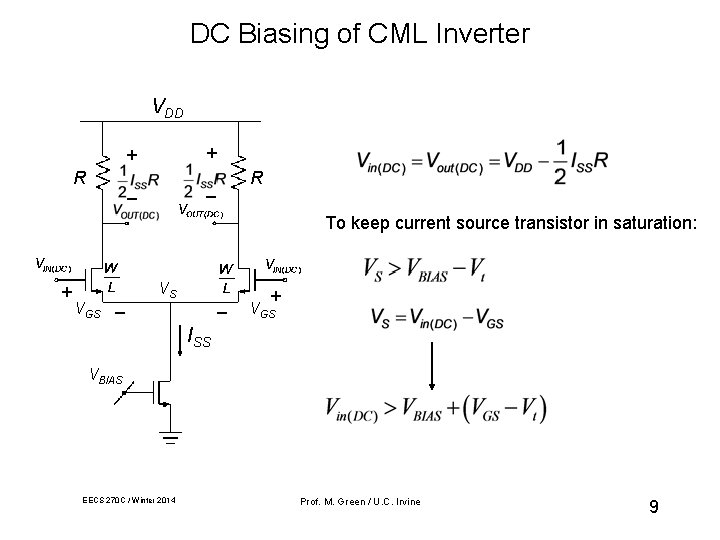
DC Biasing of CML Inverter VDD R + + _ _ R To keep current source transistor in saturation: + VGS _ VS _ + VGS ISS VBIAS EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 9

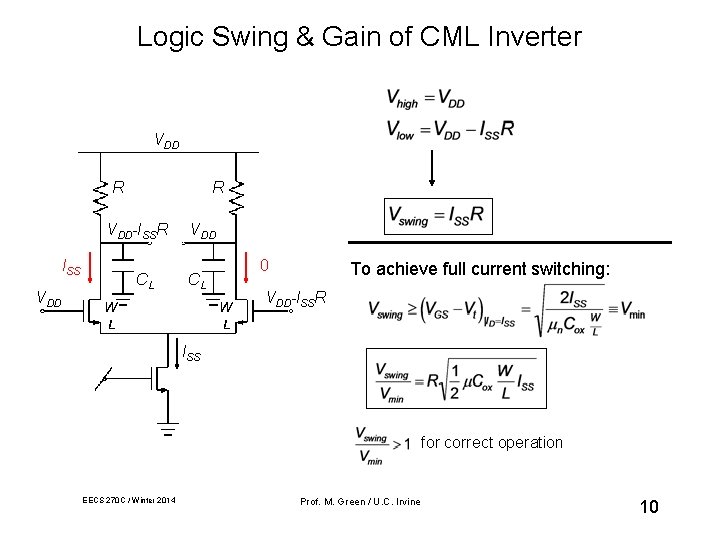
Logic Swing & Gain of CML Inverter VDD R R VDD-ISSR ISS VDD CL 0 To achieve full current switching: VDD-ISSR ISS for correct operation EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 10

Small-Signal Behavior of CML Inverter Small-signal voltage gain: rise/fall time constant: (Assuming fanout of 1) Recall for full switching EECS 270 C / Winter 2014 Note: rising & falling time constants are the same Prof. M. Green / U. C. Irvine 11

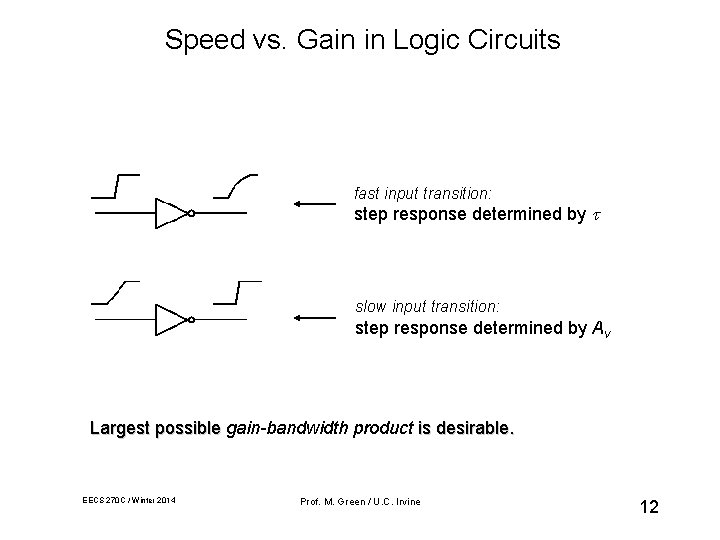
Speed vs. Gain in Logic Circuits fast input transition: step response determined by slow input transition: step response determined by Av Largest possible gain-bandwidth product is desirable. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 12

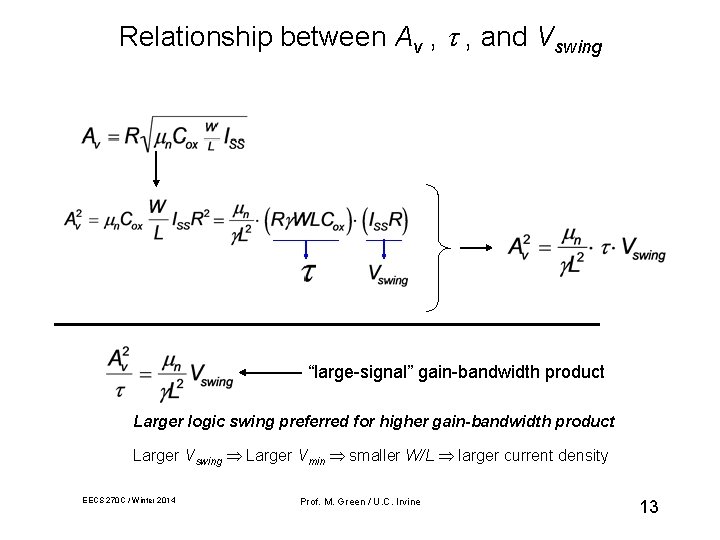
Relationship between Av , , and Vswing “large-signal” gain-bandwidth product Larger logic swing preferred for higher gain-bandwidth product Larger Vswing Larger Vmin smaller W/L larger current density EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 13

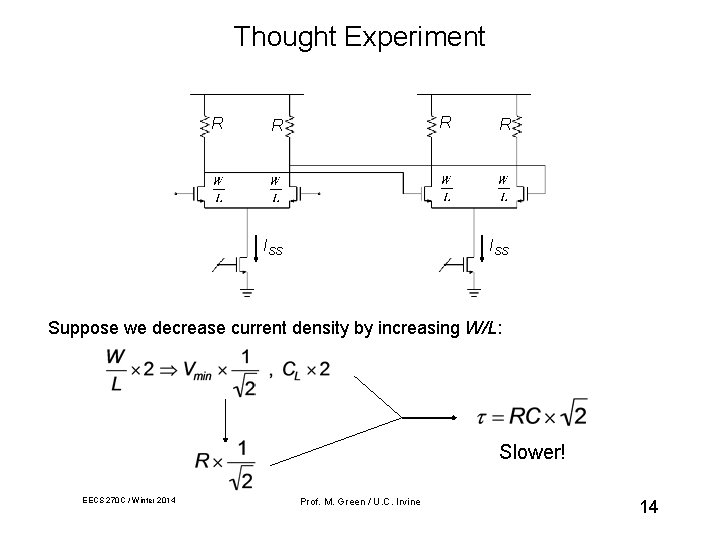
Thought Experiment R R R ISS Suppose we decrease current density by increasing W/L: Slower! EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 14

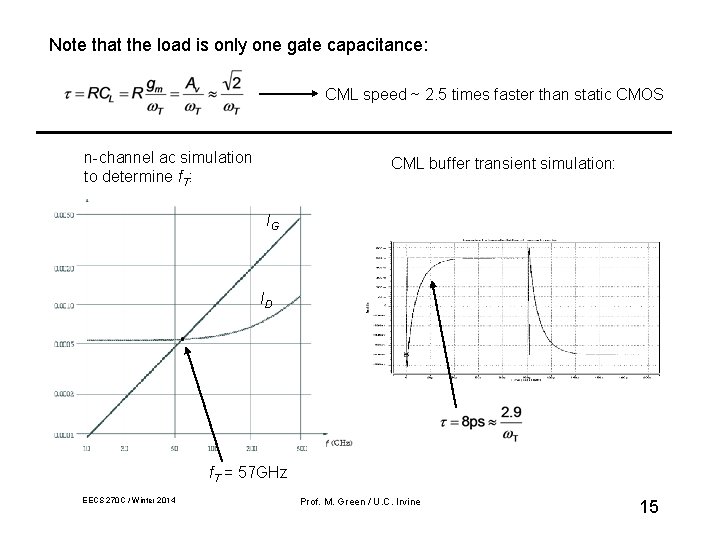
Note that the load is only one gate capacitance: CML speed ~ 2. 5 times faster than static CMOS n-channel ac simulation to determine f. T: CML buffer transient simulation: IG ID f. T = 57 GHz EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 15

Typical Vswing: • Should be large enough to allow sufficient gain-bandwidth product. • Should be small enough to prevent transistors from going into triode. * CML will still work in triode (unlike BJT), but there is no additional speed benefit. Once Vswing has been chosen, designer can trade off between gain & bandwidth by parameterizing between R & ISS: EECS 270 C / Winter 2014 Higher speed: ISS R Higher gain: R Prof. M. Green / U. C. Irvine ISS 16

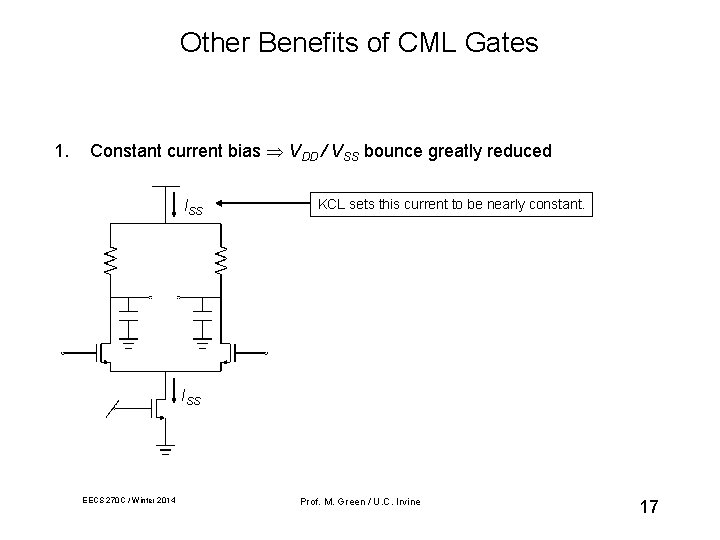
Other Benefits of CML Gates 1. Constant current bias VDD / VSS bounce greatly reduced ISS KCL sets this current to be nearly constant. ISS EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 17

data in data out clock in clock out Rs = 5 Ls = 5 n. H clock out Rs = 0 Ls = 0 clock out Rs = 5 Ls = 5 n. H EECS 270 C / Winter 2014 data out Prof. M. Green / U. C. Irvine 18

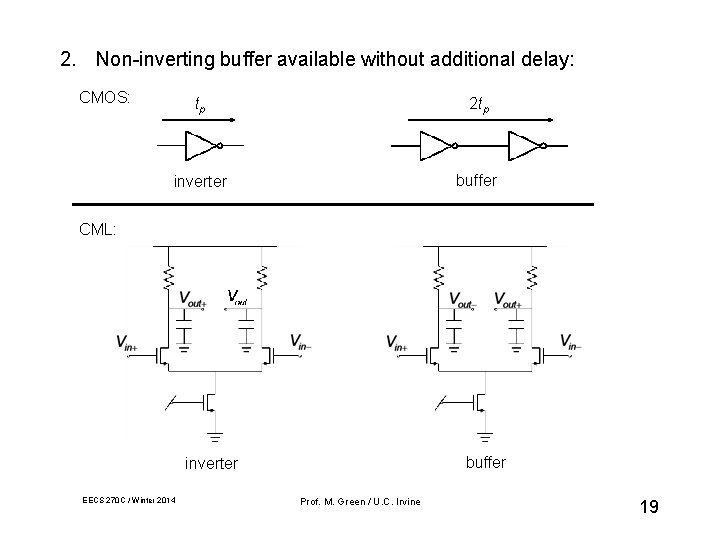
2. Non-inverting buffer available without additional delay: CMOS: tp 2 tp inverter buffer CML: buffer inverter EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 19

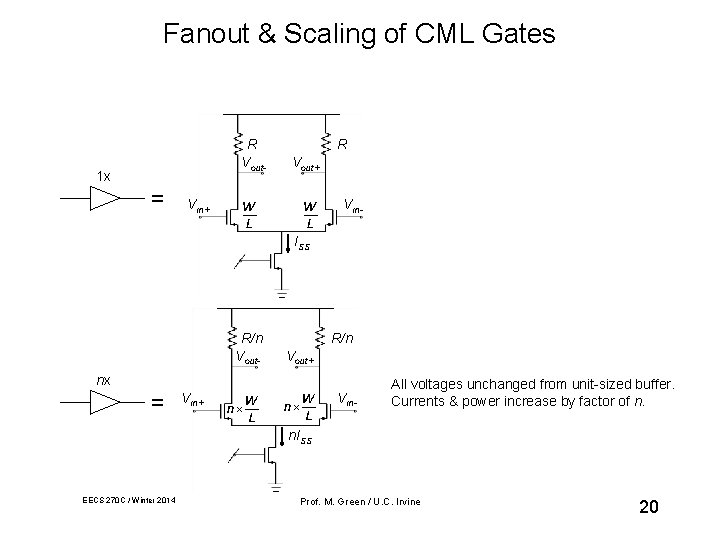
Fanout & Scaling of CML Gates R Vout- 1 x = R Vout+ Vin. ISS R/n Vout- R/n Vout+ nx = Vin+ Vin- All voltages unchanged from unit-sized buffer. Currents & power increase by factor of n. ISS EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 20

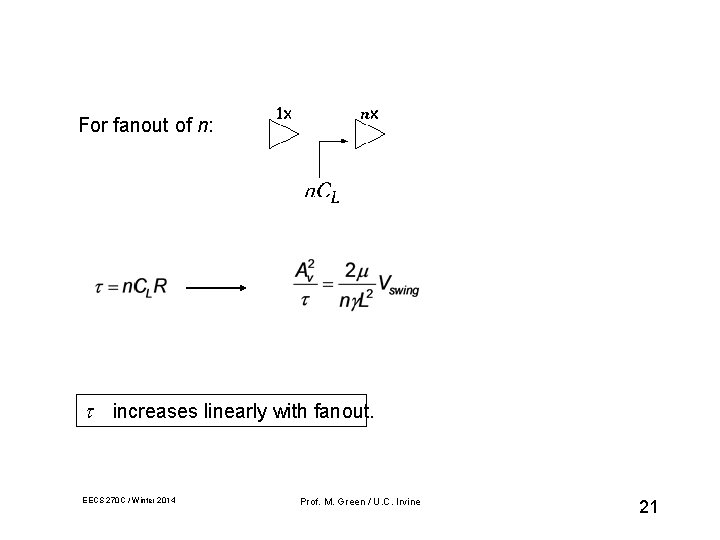
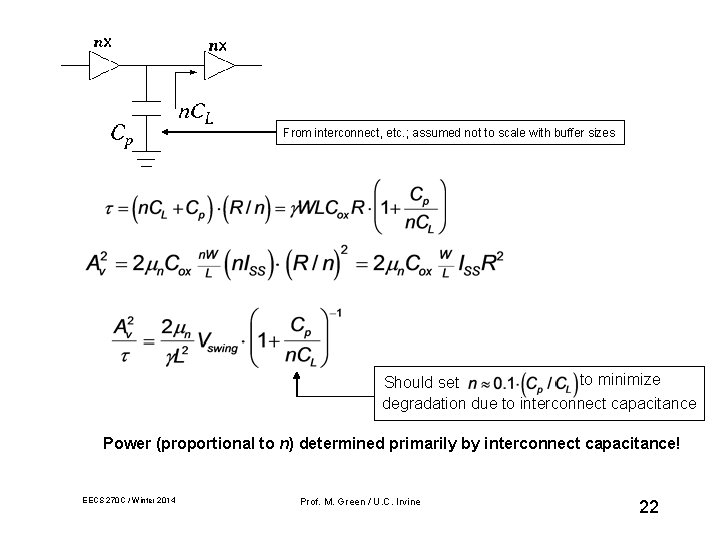
For fanout of n: increases linearly with fanout. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 21

From interconnect, etc. ; assumed not to scale with buffer sizes to minimize Should set degradation due to interconnect capacitance Power (proportional to n) determined primarily by interconnect capacitance! EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 22

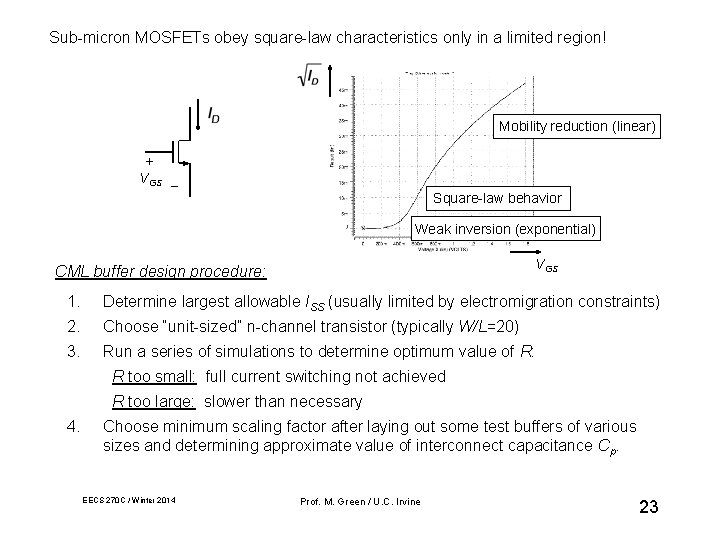
Sub-micron MOSFETs obey square-law characteristics only in a limited region! Mobility reduction (linear) + VGS _ Square-law behavior Weak inversion (exponential) VGS CML buffer design procedure: 1. Determine largest allowable ISS (usually limited by electromigration constraints) 2. Choose “unit-sized” n-channel transistor (typically W/L=20) 3. Run a series of simulations to determine optimum value of R: R too small: full current switching not achieved R too large: slower than necessary 4. Choose minimum scaling factor after laying out some test buffers of various sizes and determining approximate value of interconnect capacitance Cp. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 23

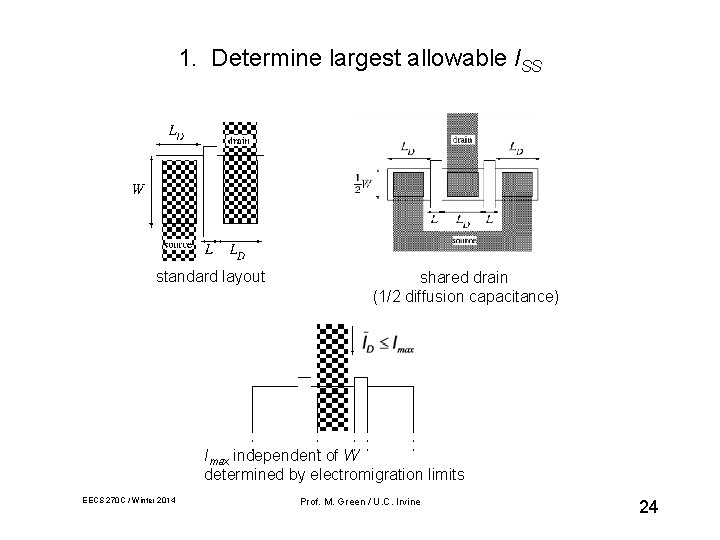
1. Determine largest allowable ISS standard layout shared drain (1/2 diffusion capacitance) Imax independent of W determined by electromigration limits EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 24

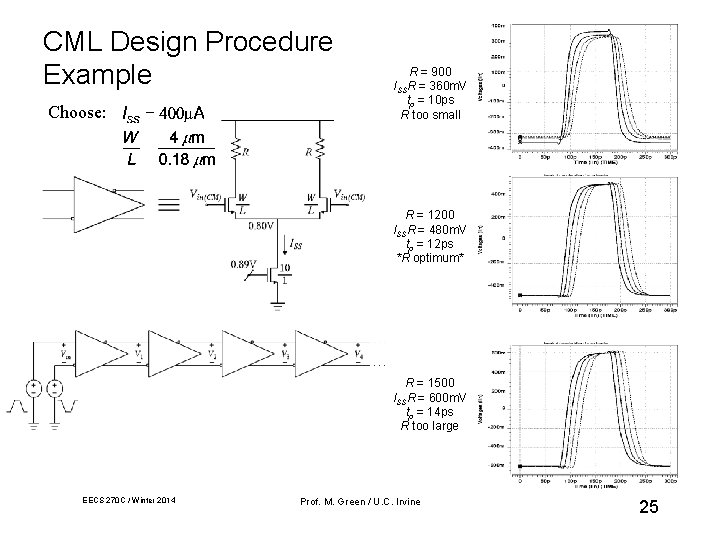
CML Design Procedure Example Choose: R = 900 ISSR = 360 m. V tp = 10 ps R too small R = 1200 ISSR = 480 m. V tp = 12 ps *R optimum* R = 1500 ISSR = 600 m. V tp = 14 ps R too large EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 25

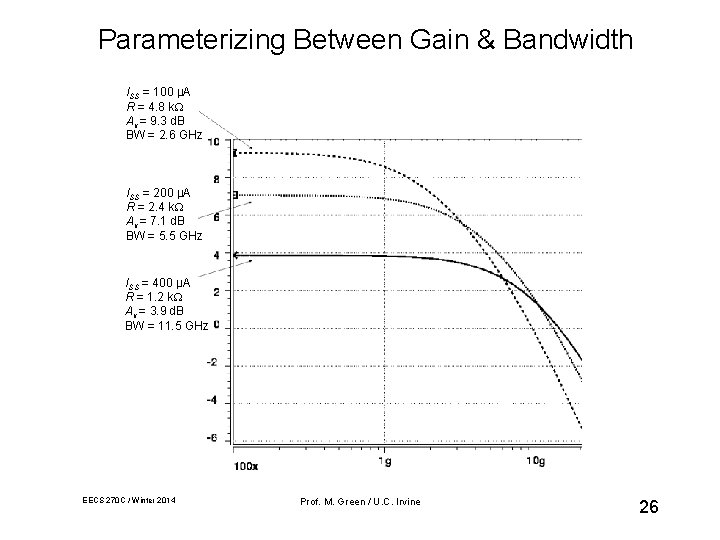
Parameterizing Between Gain & Bandwidth ISS = 100 µA R = 4. 8 k Av = 9. 3 d. B BW = 2. 6 GHz ISS = 200 µA R = 2. 4 k Av = 7. 1 d. B BW = 5. 5 GHz ISS = 400 µA R = 1. 2 k Av = 3. 9 d. B BW = 11. 5 GHz EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 26

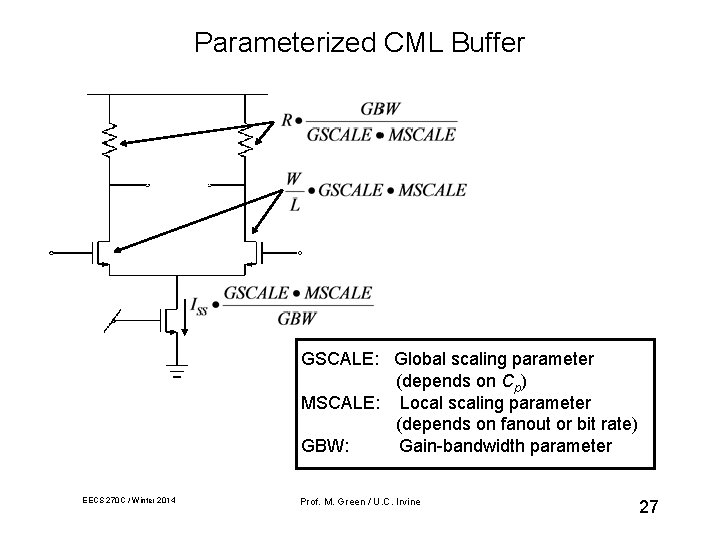
Parameterized CML Buffer GSCALE: Global scaling parameter (depends on Cp) MSCALE: Local scaling parameter (depends on fanout or bit rate) GBW: Gain-bandwidth parameter EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 27

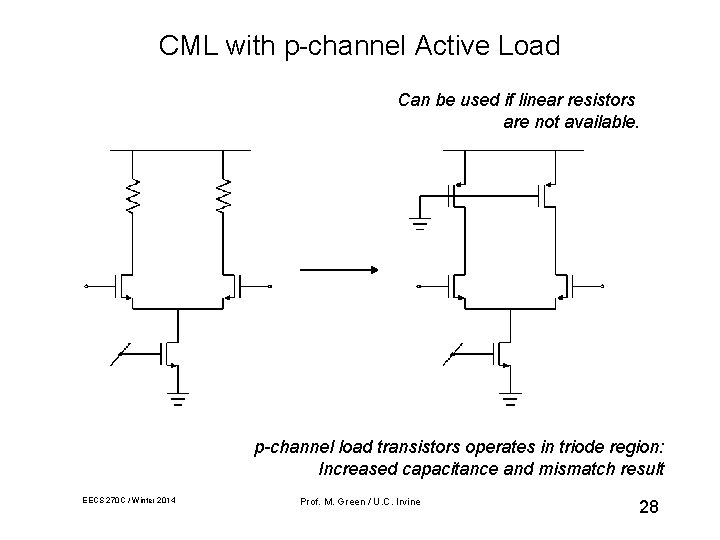
CML with p-channel Active Load Can be used if linear resistors are not available. p-channel load transistors operates in triode region: Increased capacitance and mismatch result EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 28

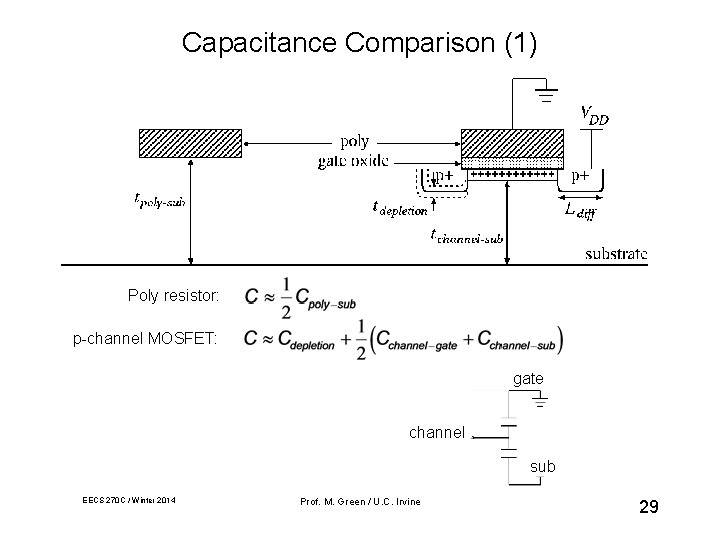
Capacitance Comparison (1) Poly resistor: p-channel MOSFET: gate channel sub EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 29

Capacitance Comparison (2) (Numbers based on TSMC 180 nm CMOS process) Cpoly-sub Cchannel-sub : 0. 13 f. F/ m 2 Cdepletion : 1. 20 f. F/ m 2 Cchannel-gate : 7. 80 f. F/ m 2 Poly resistor: Wpoly = 0. 6 Lpoly = 2. 5 = 0. 1 f. F p-channel MOSFET: Wchannel = Wdiff = 2. 5 µm Lchannel = 0. 18 µm Ldiff = 0. 3 µm = EECS 270 C / Winter 2014 0. 9 f. F + 1. 8 f. F + Prof. M. Green / U. C. Irvine . 03 f. F = 2. 8 f. F 30

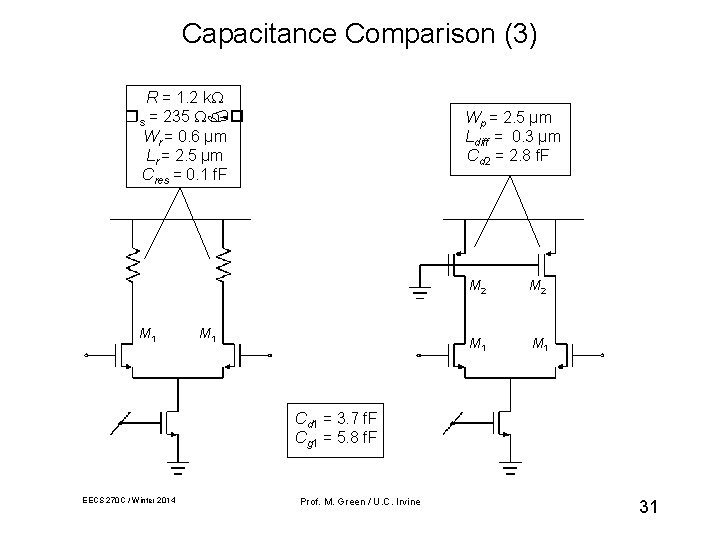
Capacitance Comparison (3) R = 1. 2 k s = 235 Wr = 0. 6 µm Lr = 2. 5 µm Cres = 0. 1 f. F M 1 Wp = 2. 5 µm Ldiff = 0. 3 µm Cd 2 = 2. 8 f. F M 1 M 2 M 1 Cd 1 = 3. 7 f. F Cg 1 = 5. 8 f. F EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 31

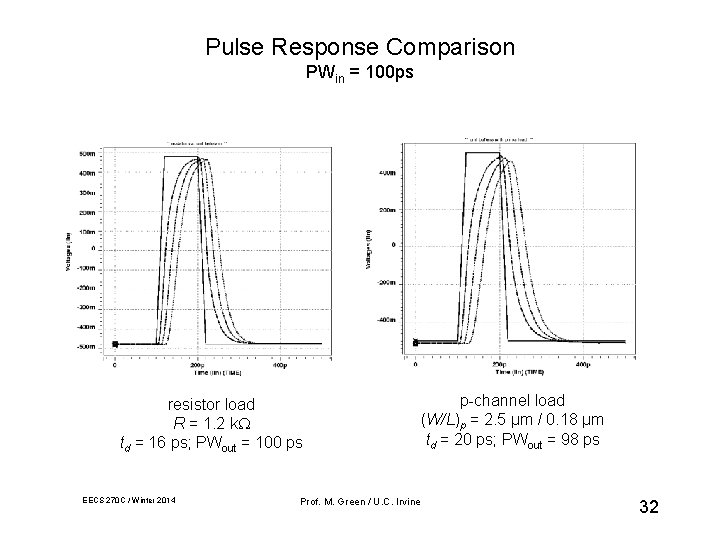
Pulse Response Comparison PWin = 100 ps resistor load R = 1. 2 k td = 16 ps; PWout = 100 ps EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine p-channel load (W/L)p = 2. 5 µm / 0. 18 µm td = 20 ps; PWout = 98 ps 32

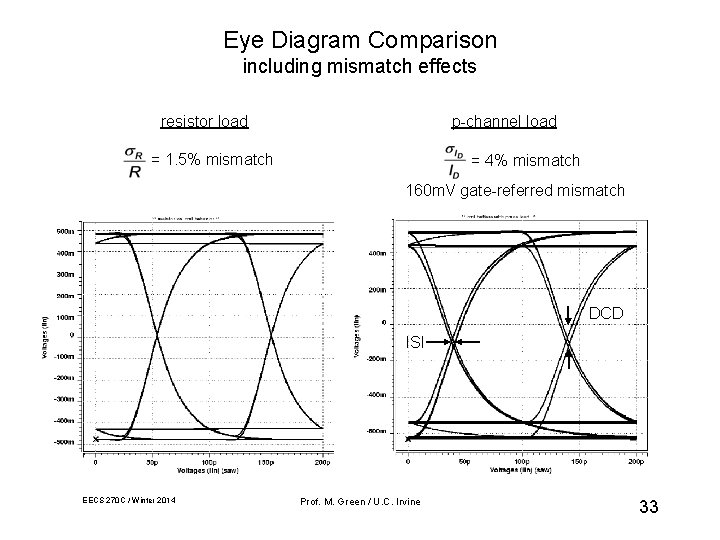
Eye Diagram Comparison including mismatch effects resistor load p-channel load = 1. 5% mismatch = 4% mismatch 160 m. V gate-referred mismatch DCD ISI EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 33

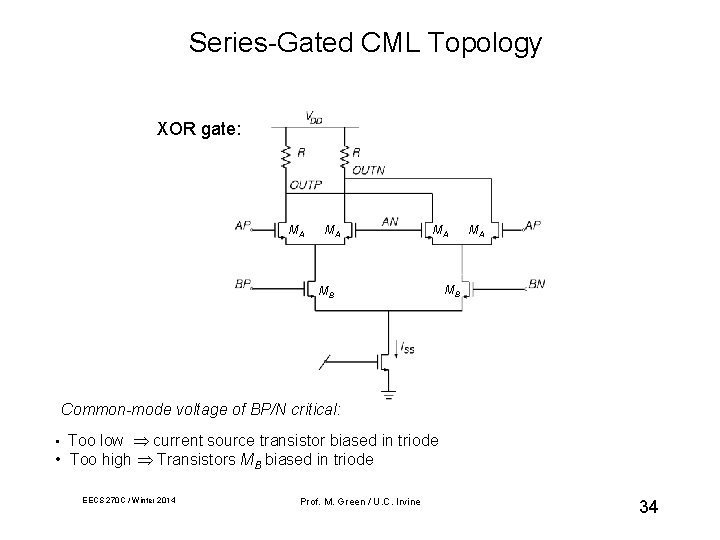
Series-Gated CML Topology XOR gate: MA MA MA MB Common-mode voltage of BP/N critical: • Too low current source transistor biased in triode • Too high Transistors MB biased in triode EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 34

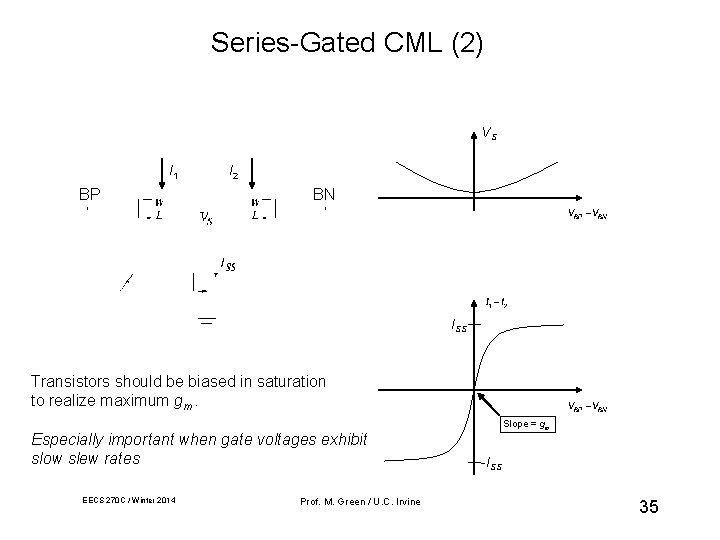
Series-Gated CML (2) VS I 1 BP I 2 BN ISS Transistors should be biased in saturation to realize maximum gm. Especially important when gate voltages exhibit slow slew rates EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine Slope = gm -ISS 35

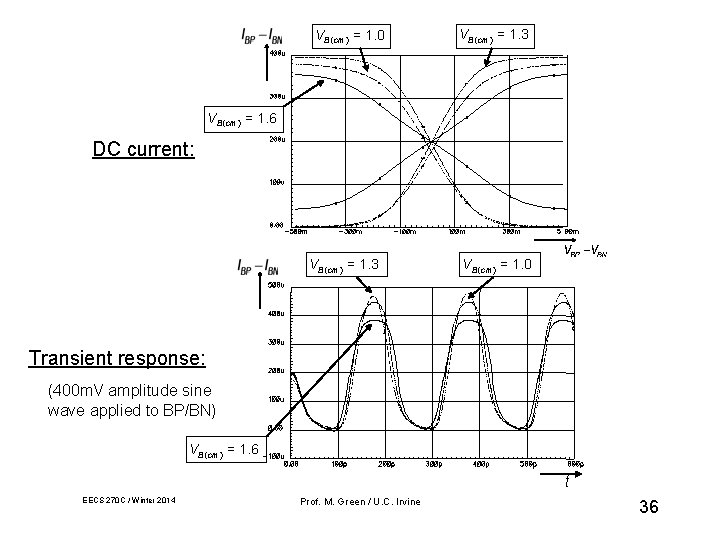
VB(cm) = 1. 0 VB(cm) = 1. 3 VB(cm) = 1. 6 DC current: VB(cm) = 1. 3 VB(cm) = 1. 0 Transient response: (400 m. V amplitude sine wave applied to BP/BN) VB(cm) = 1. 6 t EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 36

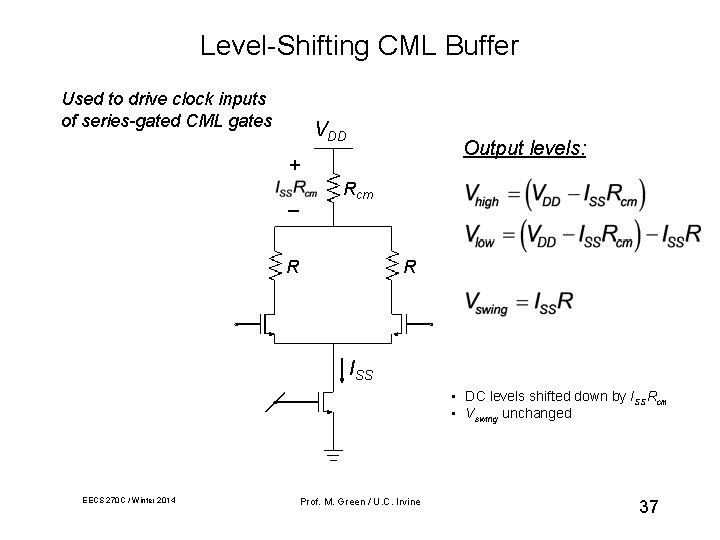
Level-Shifting CML Buffer Used to drive clock inputs of series-gated CML gates VDD Output levels: + _ Rcm R R ISS • DC levels shifted down by ISSRcm • Vswing unchanged EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 37

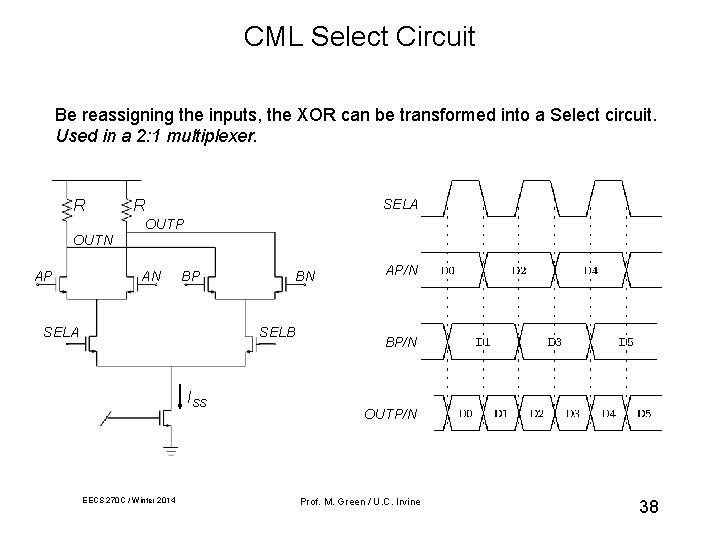
CML Select Circuit Be reassigning the inputs, the XOR can be transformed into a Select circuit. Used in a 2: 1 multiplexer. R SELA R OUTP OUTN AP AN BP SELA BN SELB ISS EECS 270 C / Winter 2014 AP/N BP/N OUTP/N Prof. M. Green / U. C. Irvine 38

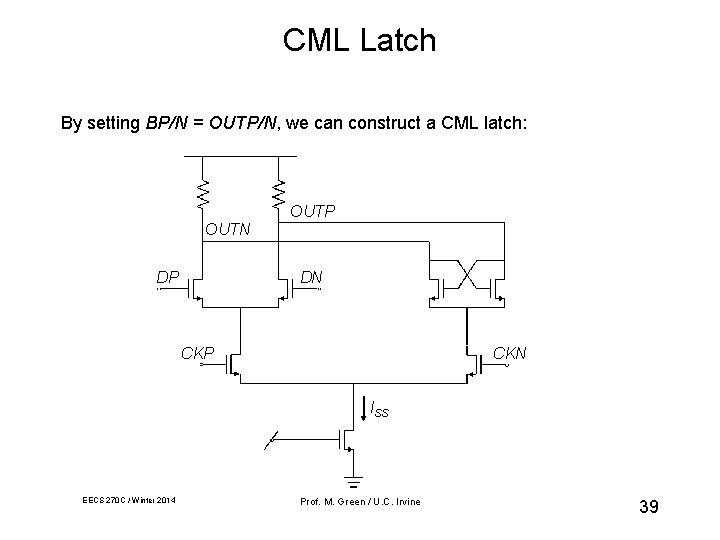
CML Latch By setting BP/N = OUTP/N, we can construct a CML latch: OUTP OUTN DP DN CKP CKN ISS EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 39

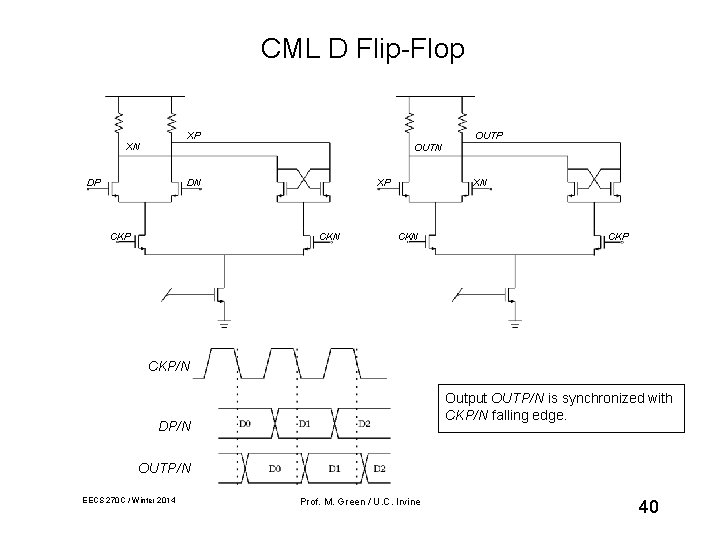
CML D Flip-Flop XP XN OUTP OUTN DP DN CKP XP CKN XN CKP CKP/N Output OUTP/N is synchronized with CKP/N falling edge. DP/N OUTP/N EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 40

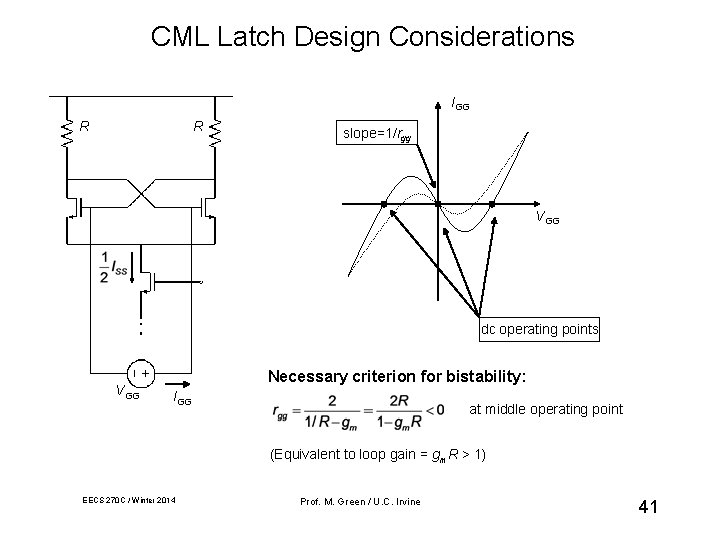
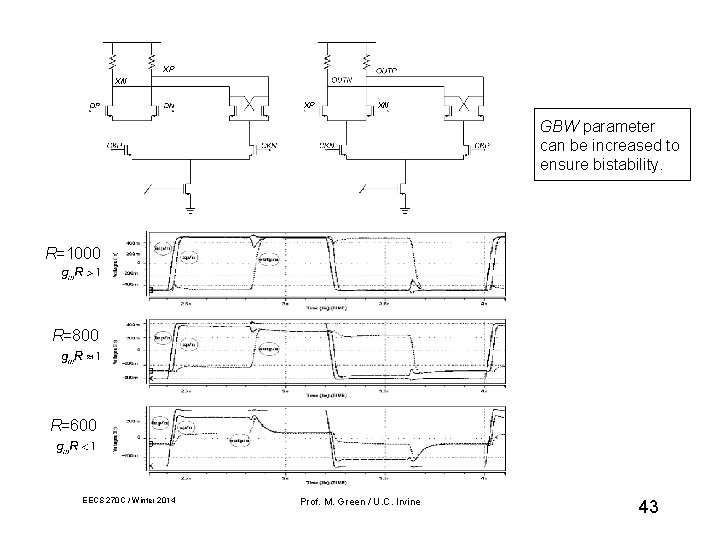
CML Latch Design Considerations IGG R R slope=1/rgg VGG dc operating points VGG Necessary criterion for bistability: IGG at middle operating point (Equivalent to loop gain = gm. R > 1) EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 41

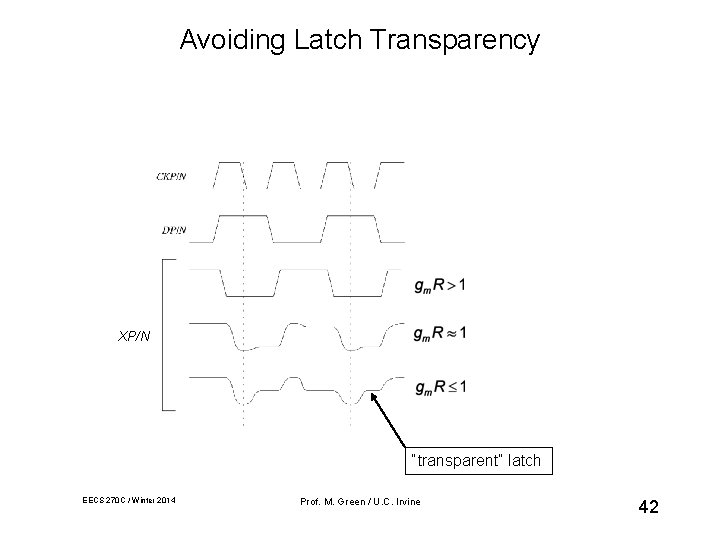
Avoiding Latch Transparency XP/N “transparent” latch EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 42

XP XN GBW parameter can be increased to ensure bistability. R=1000 R=800 R=600 EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 43

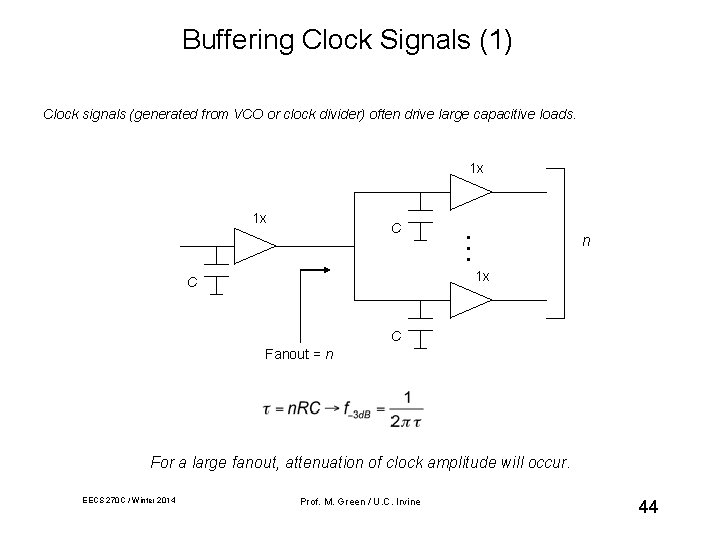
Buffering Clock Signals (1) Clock signals (generated from VCO or clock divider) often drive large capacitive loads. 1 x C … 1 x n 1 x C C Fanout = n For a large fanout, attenuation of clock amplitude will occur. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 44

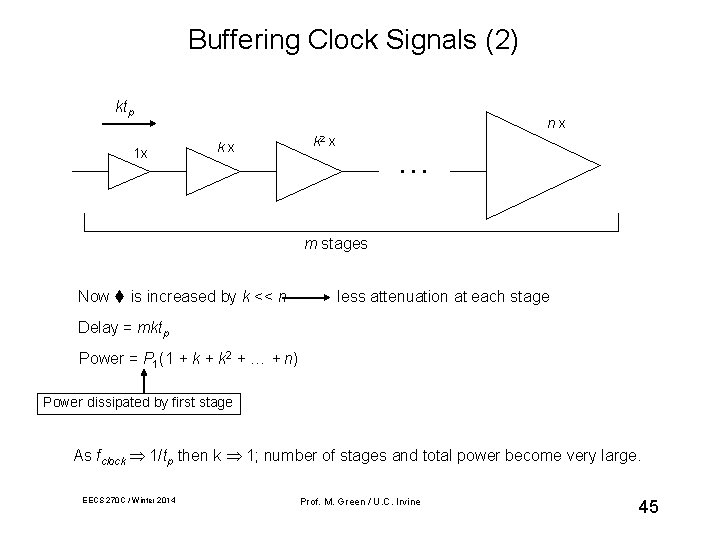
Buffering Clock Signals (2) ktp 1 x nx kx k 2 x … m stages Now is increased by k << n less attenuation at each stage Delay = mktp Power = P 1(1 + k 2 + … + n) Power dissipated by first stage As fclock 1/tp then k 1; number of stages and total power become very large. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 45

Buffering Clock Signals (3) Since clock signal is made up of a single frequency (+ harmonics), resonance can be used to increase gain with greatly reduced power dissipation. Resonant frequency: at resonance If lossless inductors were available, we could achieve high gain at any frequency simply by choosing the correct inductor value. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 46

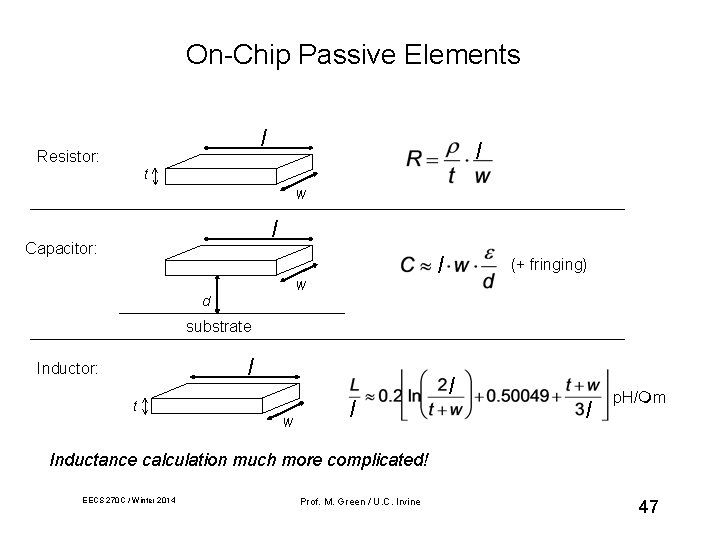
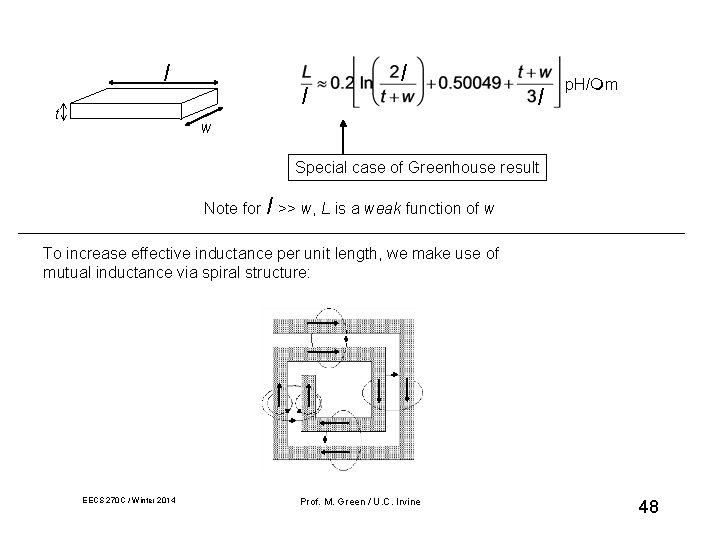
On-Chip Passive Elements l Resistor: l t w l Capacitor: l w (+ fringing) d substrate l Inductor: t w l l l p. H/ m Inductance calculation much more complicated! EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 47

l t l l l p. H/ m w Special case of Greenhouse result Note for l >> w, L is a weak function of w To increase effective inductance per unit length, we make use of mutual inductance via spiral structure: EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 48

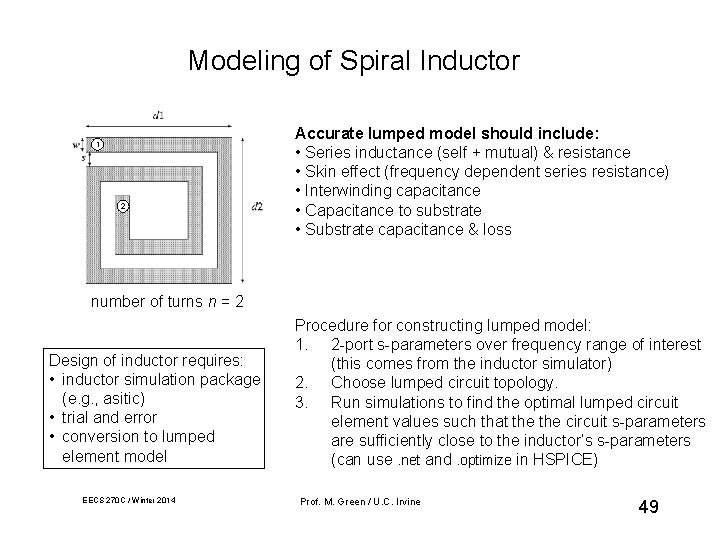
Modeling of Spiral Inductor 1 2 Accurate lumped model should include: • Series inductance (self + mutual) & resistance • Skin effect (frequency dependent series resistance) • Interwinding capacitance • Capacitance to substrate • Substrate capacitance & loss number of turns n = 2 Design of inductor requires: • inductor simulation package (e. g. , asitic) • trial and error • conversion to lumped element model EECS 270 C / Winter 2014 Procedure for constructing lumped model: 1. 2 -port s-parameters over frequency range of interest (this comes from the inductor simulator) 2. Choose lumped circuit topology. 3. Run simulations to find the optimal lumped circuit element values such that the circuit s-parameters are sufficiently close to the inductor’s s-parameters (can use. net and. optimize in HSPICE) Prof. M. Green / U. C. Irvine 49

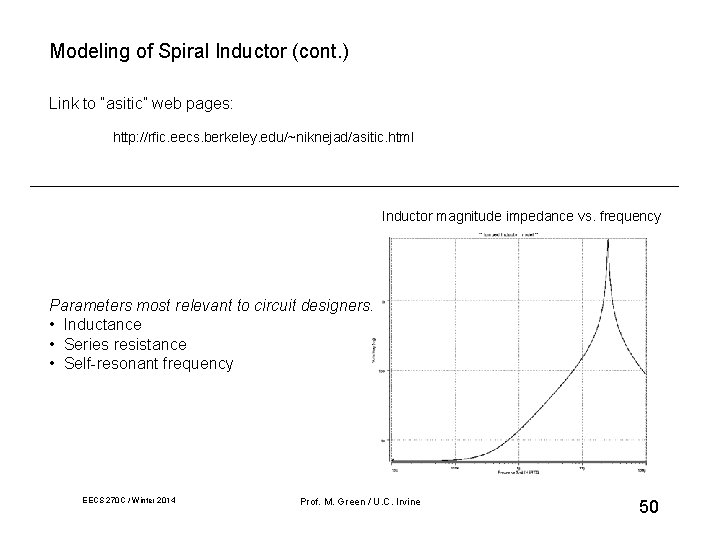
Modeling of Spiral Inductor (cont. ) Link to “asitic” web pages: http: //rfic. eecs. berkeley. edu/~niknejad/asitic. html Inductor magnitude impedance vs. frequency Parameters most relevant to circuit designers: • Inductance • Series resistance • Self-resonant frequency EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 50

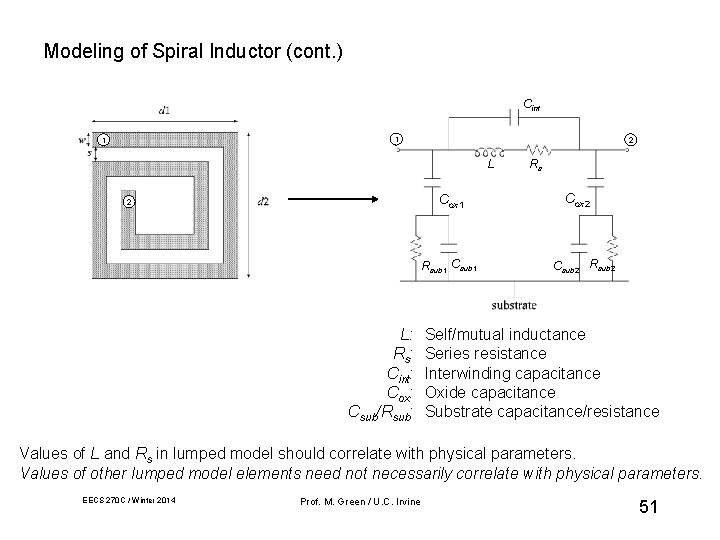
Modeling of Spiral Inductor (cont. ) Cint 1 1 2 L Cox 1 2 Rsub 1 Csub 1 L: Rs: Cint: Cox: Csub/Rsub: Rs Cox 2 Csub 2 Rsub 2 Self/mutual inductance Series resistance Interwinding capacitance Oxide capacitance Substrate capacitance/resistance Values of L and Rs in lumped model should correlate with physical parameters. Values of other lumped model elements need not necessarily correlate with physical parameters. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 51

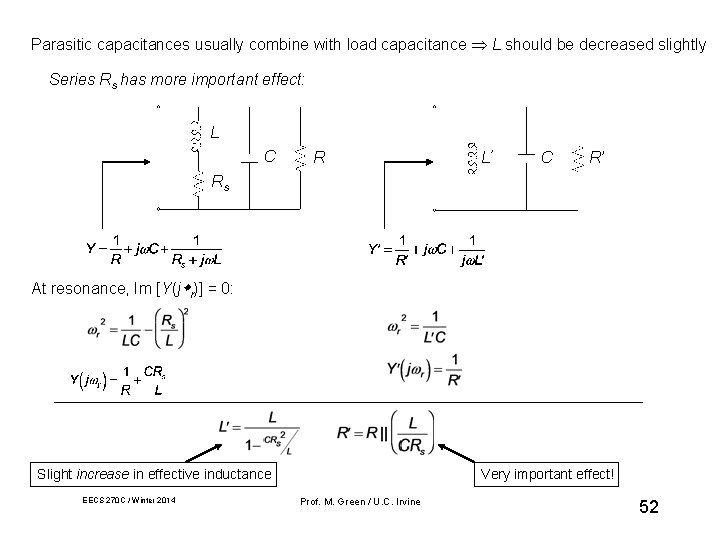
Parasitic capacitances usually combine with load capacitance L should be decreased slightly Series Rs has more important effect: L C R L' C R’ Rs At resonance, Im [Y(j r)] = 0: Slight increase in effective inductance EECS 270 C / Winter 2014 Very important effect! Prof. M. Green / U. C. Irvine 52

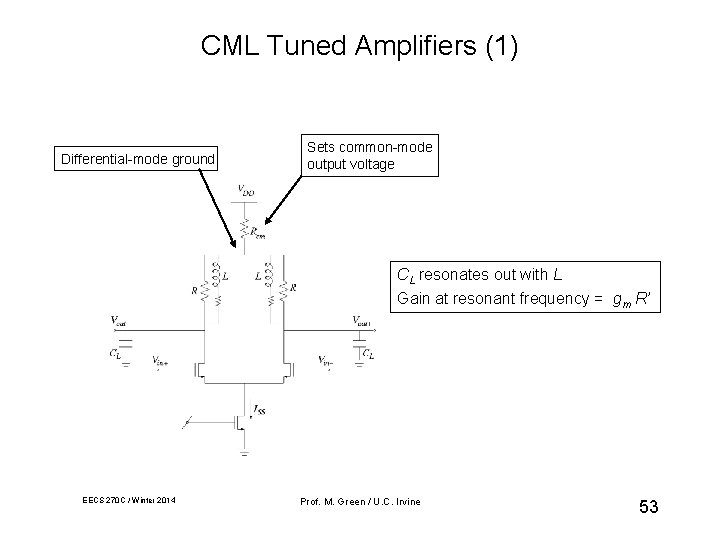
CML Tuned Amplifiers (1) Differential-mode ground Sets common-mode output voltage CL resonates out with L Gain at resonant frequency = gm R’ EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 53

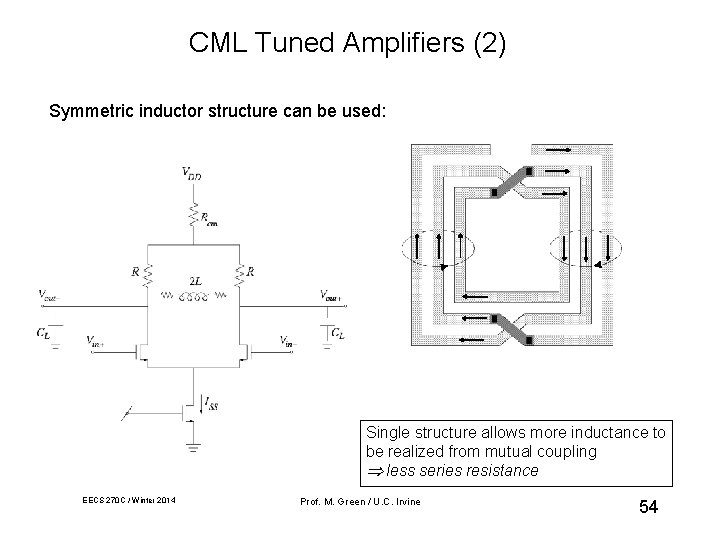
CML Tuned Amplifiers (2) Symmetric inductor structure can be used: Single structure allows more inductance to be realized from mutual coupling less series resistance EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 54

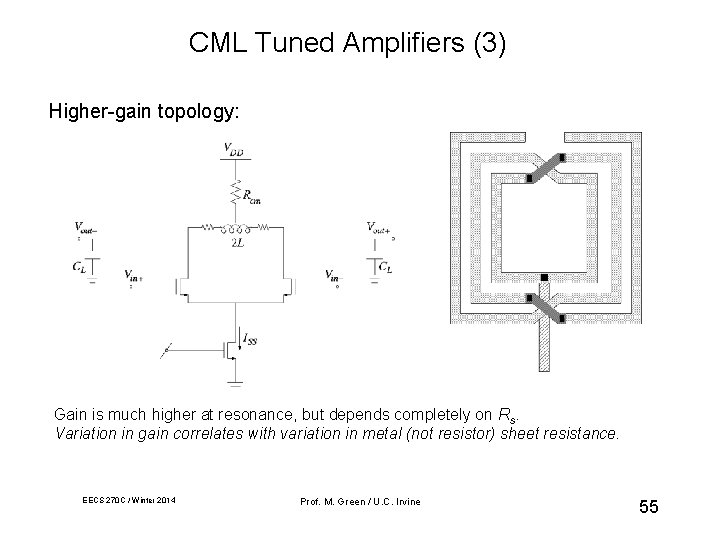
CML Tuned Amplifiers (3) Higher-gain topology: Gain is much higher at resonance, but depends completely on Rs. Variation in gain correlates with variation in metal (not resistor) sheet resistance. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 55

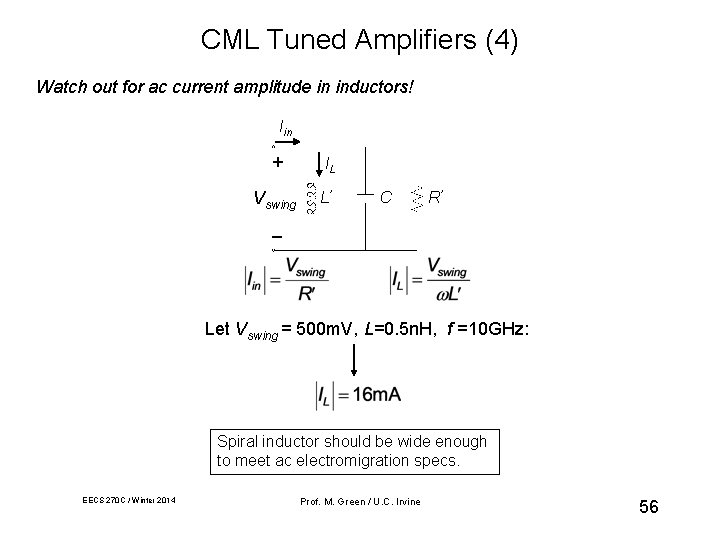
CML Tuned Amplifiers (4) Watch out for ac current amplitude in inductors! Iin + IL Vswing L’ C R’ _ Let Vswing = 500 m. V, L=0. 5 n. H, f =10 GHz: Spiral inductor should be wide enough to meet ac electromigration specs. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 56

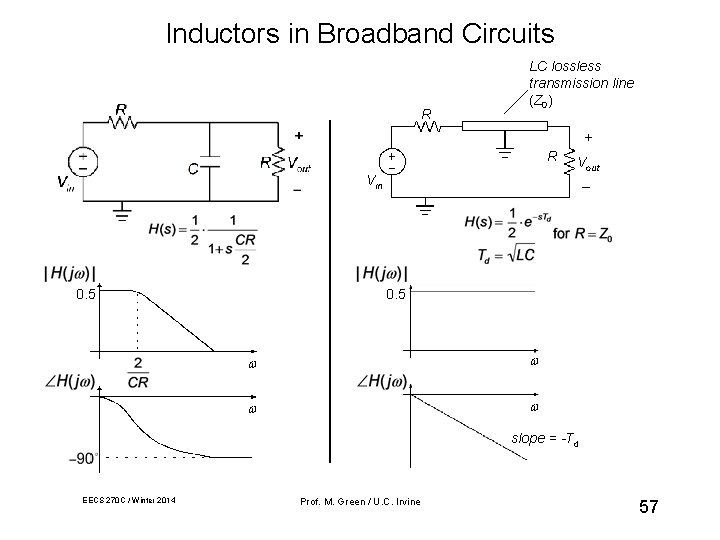
Inductors in Broadband Circuits R LC lossless transmission line (Z 0) + R Vin 0. 5 Vout _ 0. 5 slope = -Td EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 57

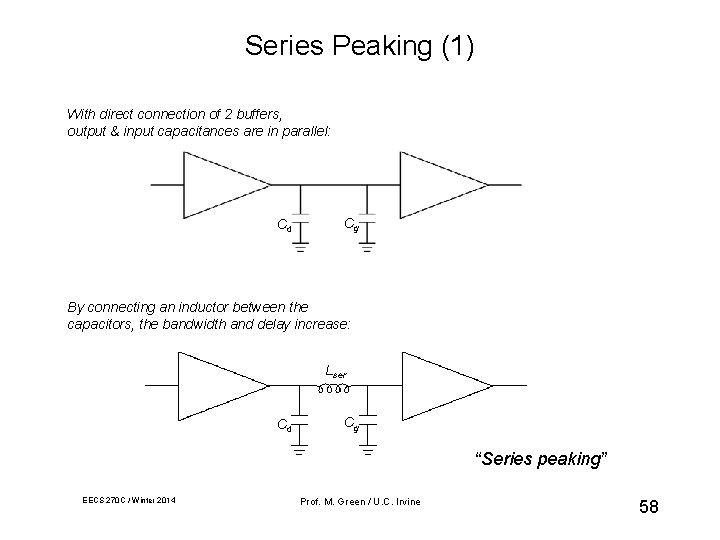
Series Peaking (1) With direct connection of 2 buffers, output & input capacitances are in parallel: Cd Cg By connecting an inductor between the capacitors, the bandwidth and delay increase: Lser Cd Cg “Series peaking” EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 58

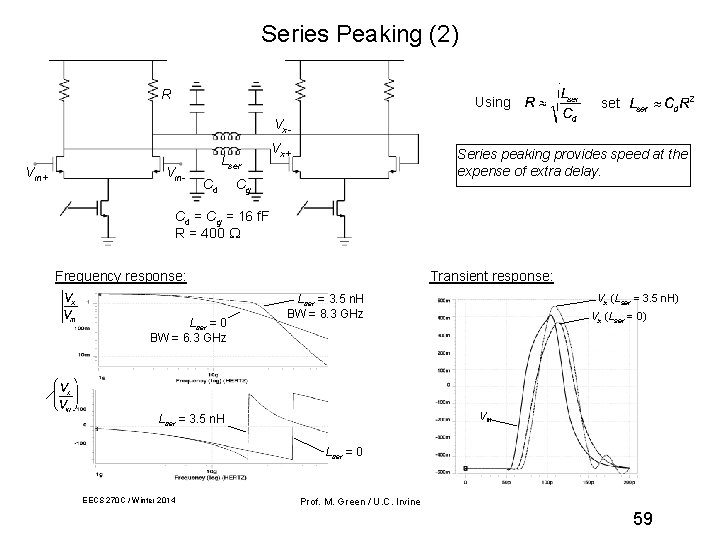
Series Peaking (2) R Using set Vx. Vin+ Vin- Lser Cd Vx+ Series peaking provides speed at the expense of extra delay. Cg Cd = Cg = 16 f. F R = 400 Frequency response: Lser = 0 BW = 6. 3 GHz Transient response: Vx (Lser = 3. 5 n. H) Lser = 3. 5 n. H BW = 8. 3 GHz Vx (Lser = 0) Vin Lser = 3. 5 n. H Lser = 0 EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 59

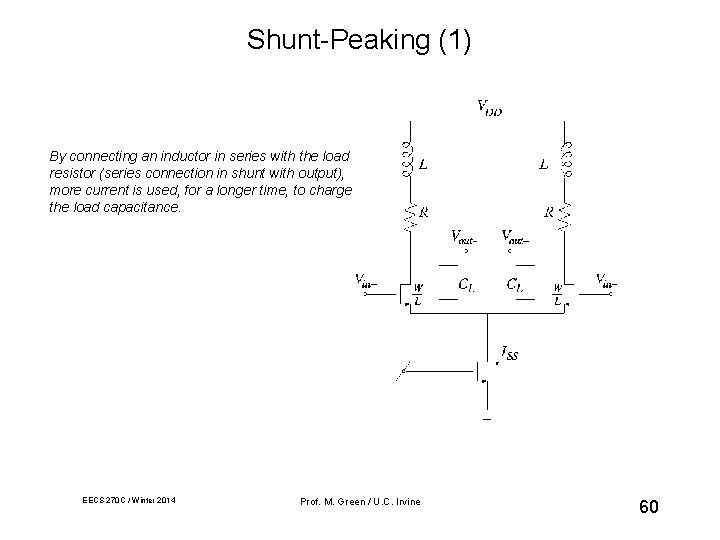
Shunt-Peaking (1) By connecting an inductor in series with the load resistor (series connection in shunt with output), more current is used, for a longer time, to charge the load capacitance. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 60

Properties of Shunt-Peaking Frequency response: CL Resonant frequency: Im s X OX Re s L = 0: L ≠ 0: zero at s = −R/L pole at s = − 1/RC additional pole at s ≈ −(1/CR + R/L) EECS 270 C / Winter 2014 No resonance for Prof. M. Green / U. C. Irvine 61

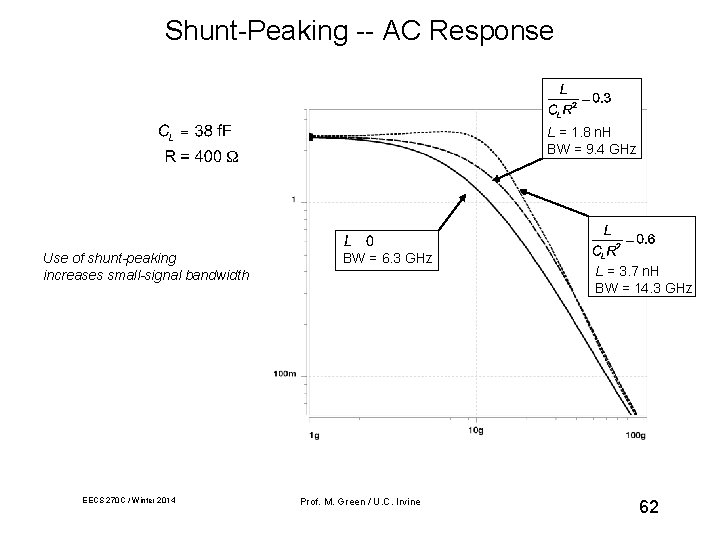
Shunt-Peaking -- AC Response L = 1. 8 n. H BW = 9. 4 GHz Use of shunt-peaking increases small-signal bandwidth EECS 270 C / Winter 2014 BW = 6. 3 GHz Prof. M. Green / U. C. Irvine L = 3. 7 n. H BW = 14. 3 GHz 62

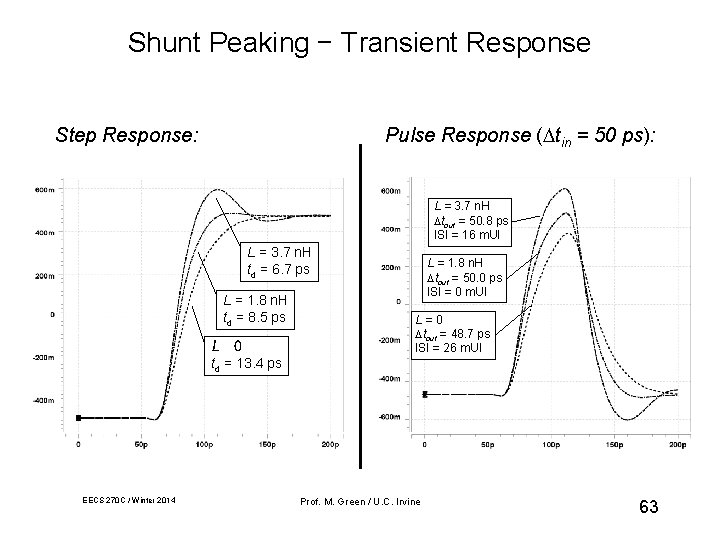
Shunt Peaking − Transient Response Step Response: Pulse Response (Dtin = 50 ps): L = 3. 7 n. H Dtout = 50. 8 ps ISI = 16 m. UI L = 3. 7 n. H td = 6. 7 ps L = 1. 8 n. H td = 8. 5 ps L = 1. 8 n. H Dtout = 50. 0 ps ISI = 0 m. UI L=0 Dtout = 48. 7 ps ISI = 26 m. UI td = 13. 4 ps EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 63

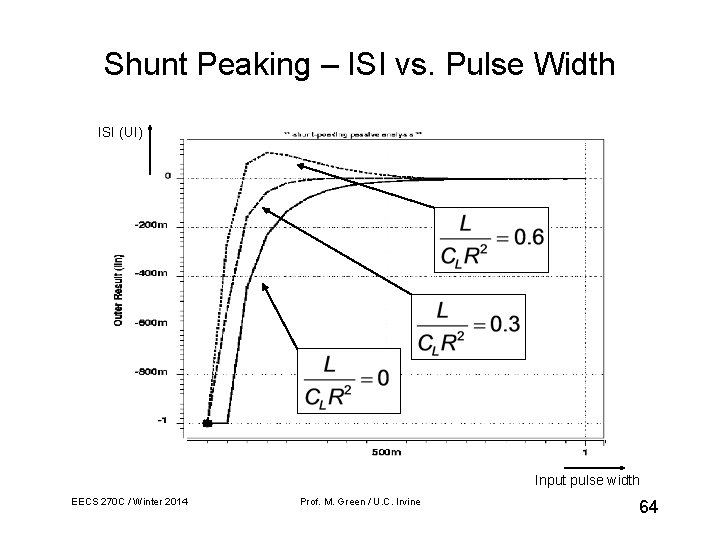
Shunt Peaking – ISI vs. Pulse Width ISI (UI) Input pulse width EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 64

Other Advantages of Shunt-Peaking • CML load is passive & linear • Can be shown to be very robust in the presence of parasitic series resistance and shunt capacitance inductors can be placed far away from other CML circuit elements. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 65

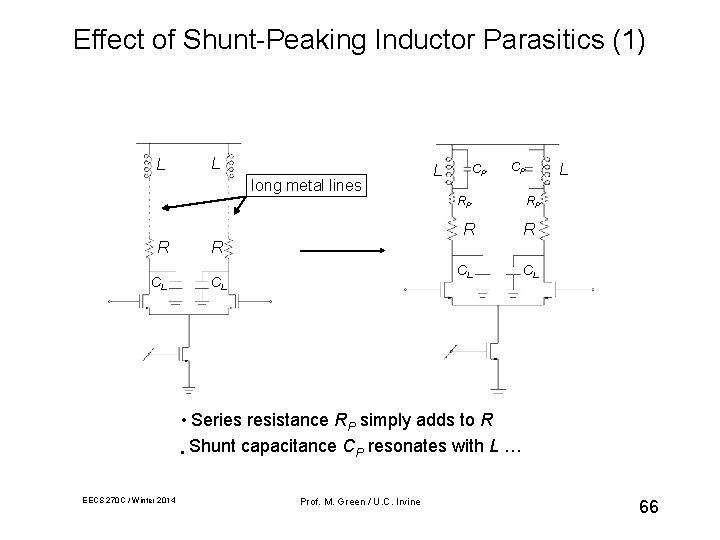
Effect of Shunt-Peaking Inductor Parasitics (1) L L long metal lines L CP CP RP R R CL CL L RP R R CL CL • Series resistance RP simply adds to R • Shunt EECS 270 C / Winter 2014 capacitance CP resonates with L … Prof. M. Green / U. C. Irvine 66

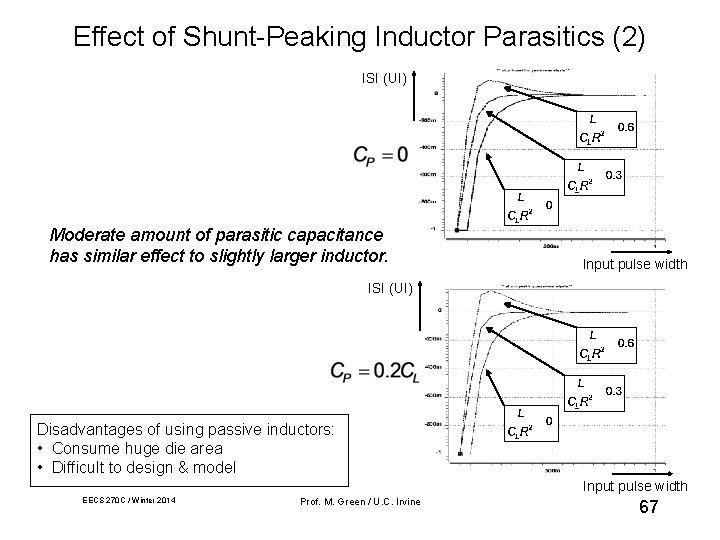
Effect of Shunt-Peaking Inductor Parasitics (2) ISI (UI) Moderate amount of parasitic capacitance has similar effect to slightly larger inductor. Input pulse width ISI (UI) Disadvantages of using passive inductors: • Consume huge die area • Difficult to design & model Input pulse width EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 67

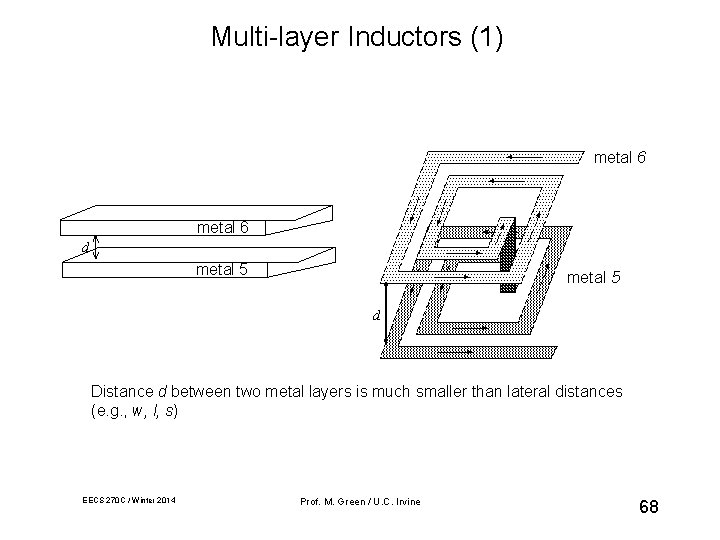
Multi-layer Inductors (1) metal 6 d metal 5 d Distance d between two metal layers is much smaller than lateral distances (e. g. , w, l, s) EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 68

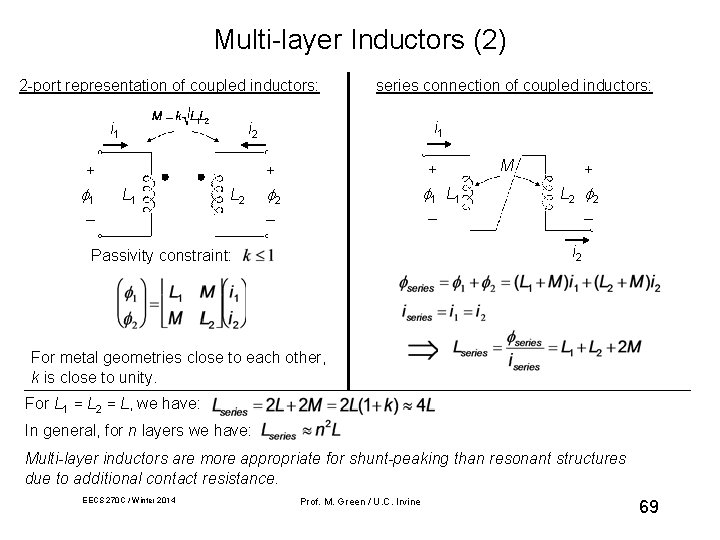
Multi-layer Inductors (2) 2 -port representation of coupled inductors: i 1 _ i 1 i 2 + 1 series connection of coupled inductors: + + L 1 L 2 1 L 1 2 _ _ M + L 2 2 _ i 2 Passivity constraint: For metal geometries close to each other, k is close to unity. For L 1 = L 2 = L, we have: In general, for n layers we have: Multi-layer inductors are more appropriate for shunt-peaking than resonant structures due to additional contact resistance. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 69

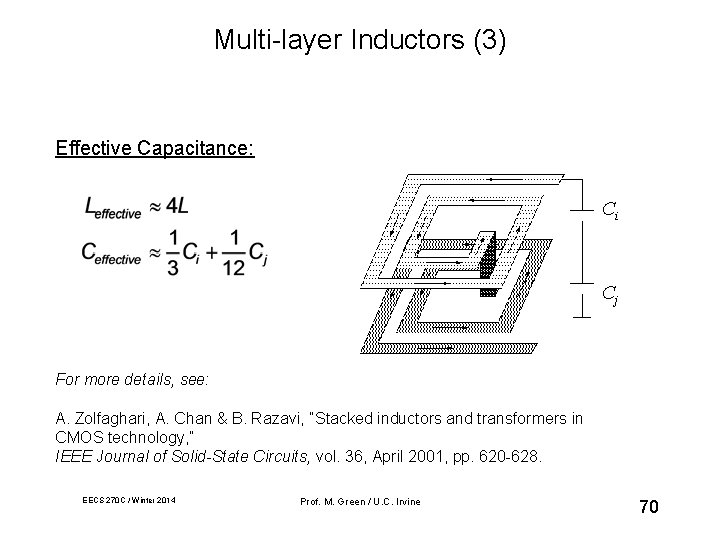
Multi-layer Inductors (3) Effective Capacitance: Ci Cj For more details, see: A. Zolfaghari, A. Chan & B. Razavi, “Stacked inductors and transformers in CMOS technology, ” IEEE Journal of Solid-State Circuits, vol. 36, April 2001, pp. 620 -628. EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 70

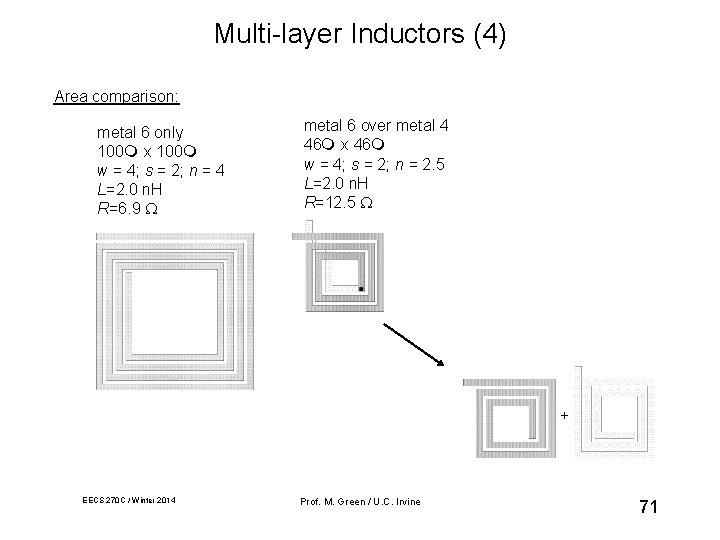
Multi-layer Inductors (4) Area comparison: metal 6 only 100 x 100 w = 4; s = 2; n = 4 L=2. 0 n. H R=6. 9 metal 6 over metal 4 46 x 46 w = 4; s = 2; n = 2. 5 L=2. 0 n. H R=12. 5 + EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 71

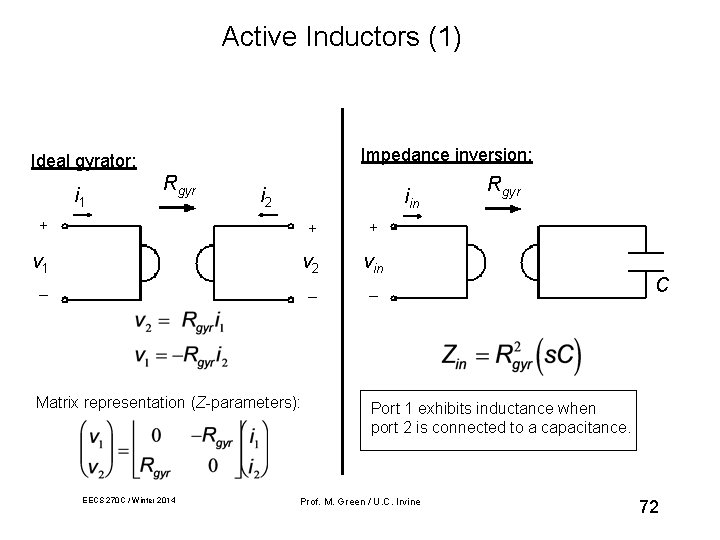
Active Inductors (1) Impedance inversion: Ideal gyrator: i 1 Rgyr i 2 iin + + + v 1 v 2 vin _ _ _ Matrix representation (Z-parameters): EECS 270 C / Winter 2014 Rgyr C Port 1 exhibits inductance when port 2 is connected to a capacitance. Prof. M. Green / U. C. Irvine 72

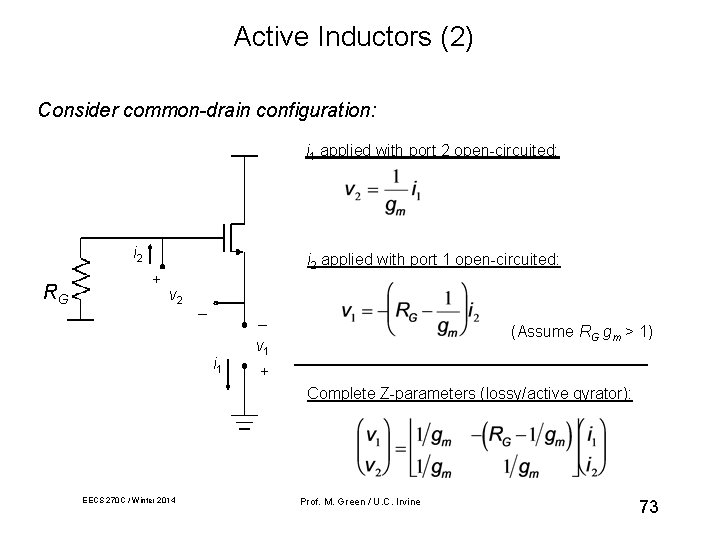
Active Inductors (2) Consider common-drain configuration: i 1 applied with port 2 open-circuited: i 2 RG + i 2 applied with port 1 open-circuited: v 2 _ _ i 1 (Assume RG gm > 1) v 1 + Complete Z-parameters (lossy/active gyrator): EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 73

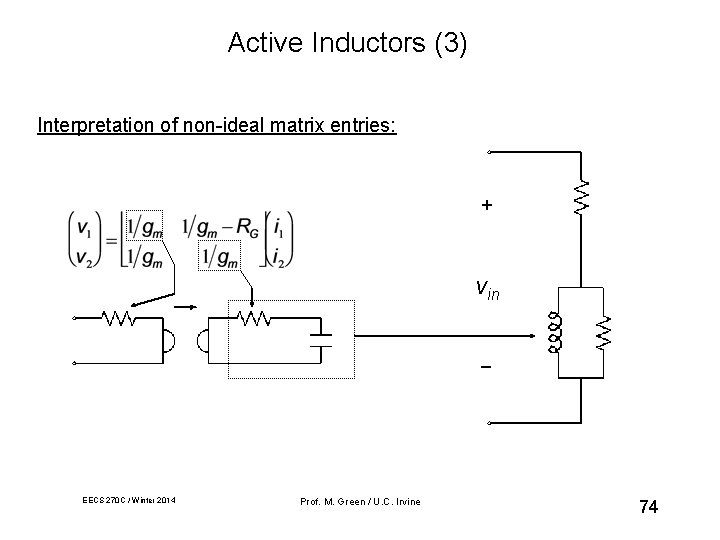
Active Inductors (3) Interpretation of non-ideal matrix entries: + vin _ EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 74

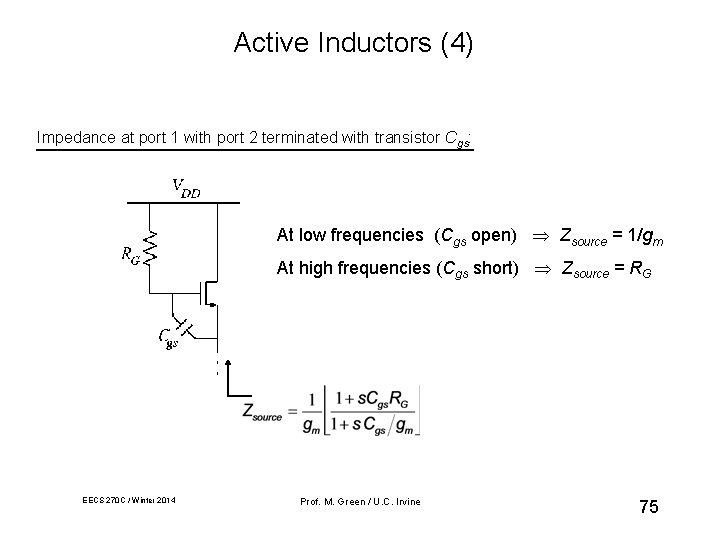
Active Inductors (4) Impedance at port 1 with port 2 terminated with transistor Cgs: At low frequencies (Cgs open) Zsource = 1/gm At high frequencies (Cgs short) Zsource = RG EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 75

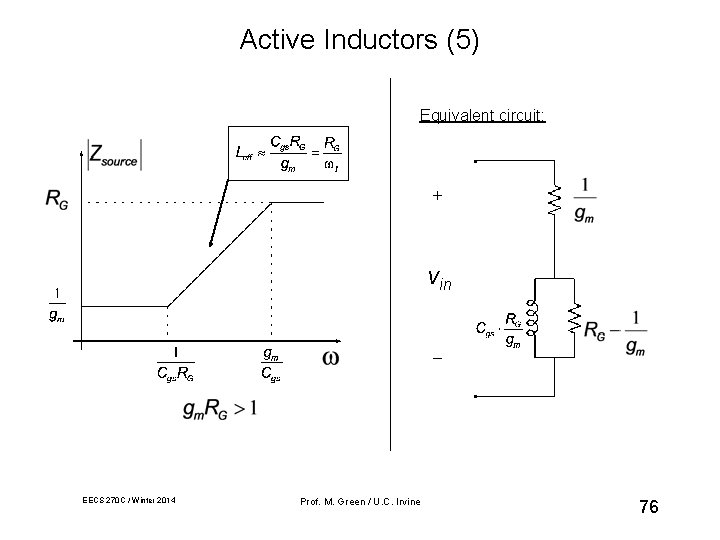
Active Inductors (5) Equivalent circuit: + vin _ EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 76

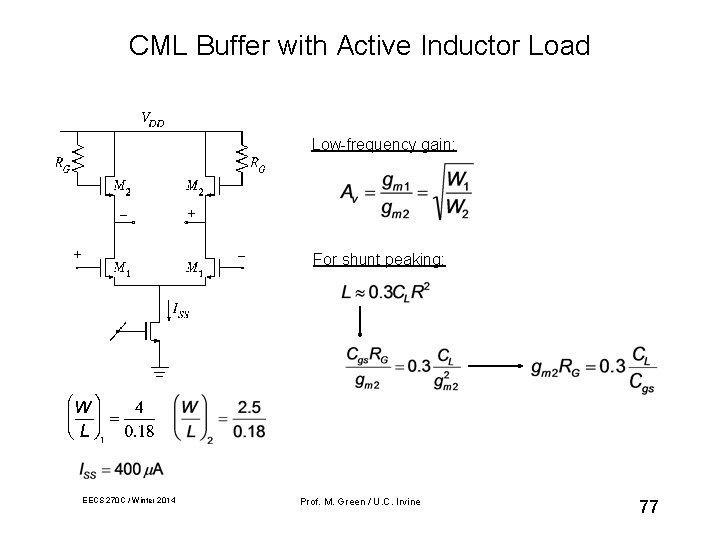
CML Buffer with Active Inductor Load Low-frequency gain: For shunt peaking: EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 77

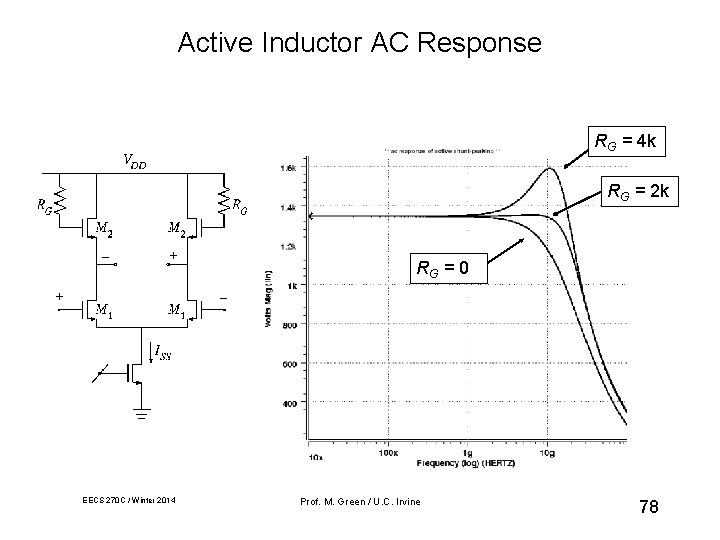
Active Inductor AC Response RG = 4 k RG = 2 k RG = 0 EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 78

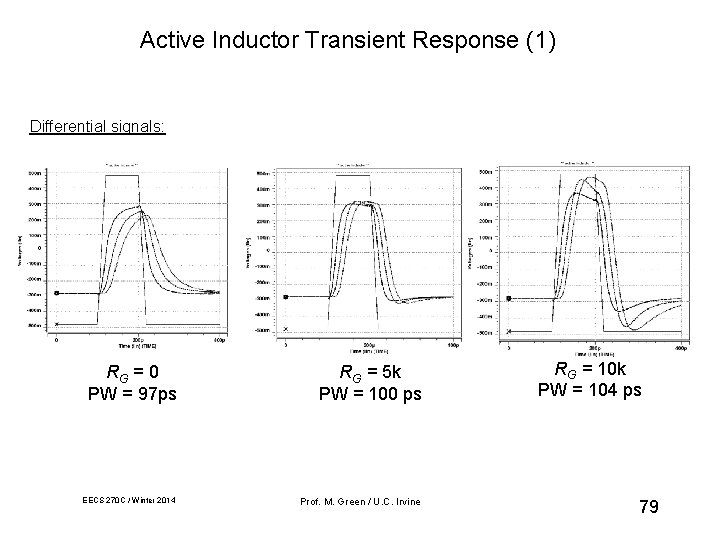
Active Inductor Transient Response (1) Differential signals: RG = 0 PW = 97 ps RG = 5 k PW = 100 ps EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine RG = 10 k PW = 104 ps 79

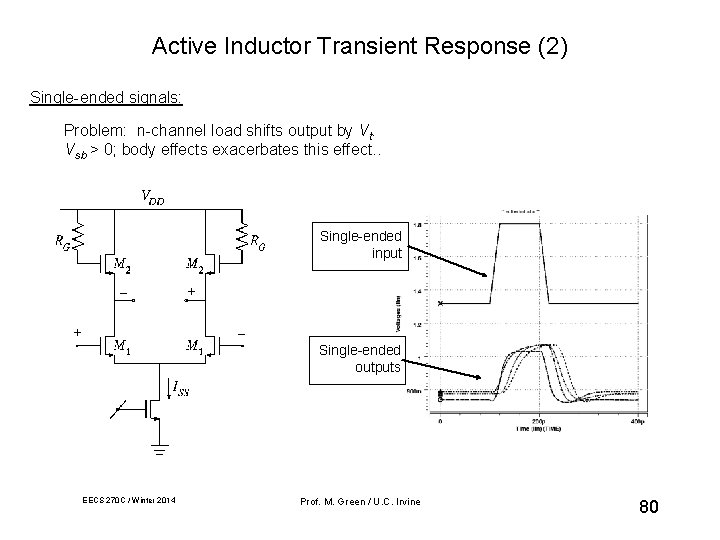
Active Inductor Transient Response (2) Single-ended signals: Problem: n-channel load shifts output by Vt. Vsb > 0; body effects exacerbates this effect. . Single-ended input Single-ended outputs EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 80

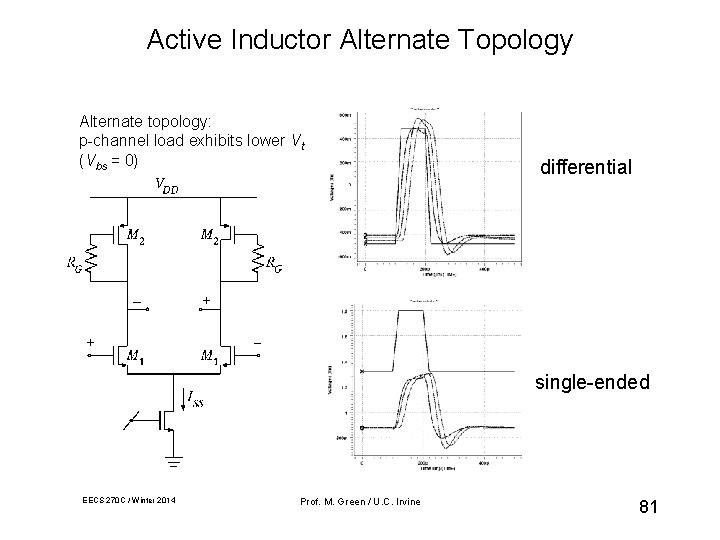
Active Inductor Alternate Topology Alternate topology: p-channel load exhibits lower Vt (Vbs = 0) differential single-ended EECS 270 C / Winter 2014 Prof. M. Green / U. C. Irvine 81