Advances in Random Matrix Theory stochastic eigenanalysis Alan

Advances in Random Matrix Theory (stochastic eigenanalysis) Alan Edelman MIT: Dept of Mathematics, Computer Science AI Laboratories 11/21/2020 1

Stochastic Eigenanalysis v. Counterpart to stochastic differential equations v. Emphasis on applications to engineering & finance v. Beautiful mathematics: v. Random Matrix Theory v. Free Probability v. Raw Material from v. Physics v. Combinatorics v. Numerical Linear Algebra v. Multivariate Statistics 11/21/2020 2

Scalars, Vectors, Matrices Mathematics: v Computation: v Statistics: v Notation = power & less ink! Use those caches! Classical, Multivariate, Modern Random Matrix Theory The Stochastic Eigenproblem * Mathematics of probabilistic linear algebra * Emerging Computational Algorithms * Emerging Statistical Techniques Ideas from numerical computation that stand the test of time are right for mathematics! 3

Open Questions v Find new applications of spacing (or other) statistics v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 4

Wigner’s Semi-Circle v The classical & most famous rand eig v Let S = random symmetric Gaussian v MATLAB: A=randn(n); S=( A+A’)/2; v S known as the Hermite Ensemble v Normalized eigenvalue histogram is v Precise theorem a semi-circle statements require n etc. 5

Wigner’s Semi-Circle v The classical & most famous rand eig v Let S = random symmetric Gaussian v MATLAB: A=randn(n); S=( A+A’)/2; v S known as the Hermite Ensemble v Normalized eigenvalue histogram is v Precise theorem a semi-circle statements require n etc. n x n iid standard normals 6

Wigner’s Semi-Circle v The classical & most famous rand eig v Let S = random symmetric Gaussian v MATLAB: A=randn(n); S=( A+A’)/2; v S known as the Hermite Ensemble v Normalized eigenvalue histogram is v Precise theorem a semi-circle statements require n etc. 7

Wigner’s original proof Compute E(tr A 2 p) as n ∞ v Terms with too many indices, have some element with power 1. Vanishes with mean 0. v Terms with too few indices: not enough to be relevant as n ∞ v Leaves only a Catalan number left: Cp=(2 p p )/(p+1) for the moments when all is said and done v Semi-circle only distribution with Catalan number moments v 8

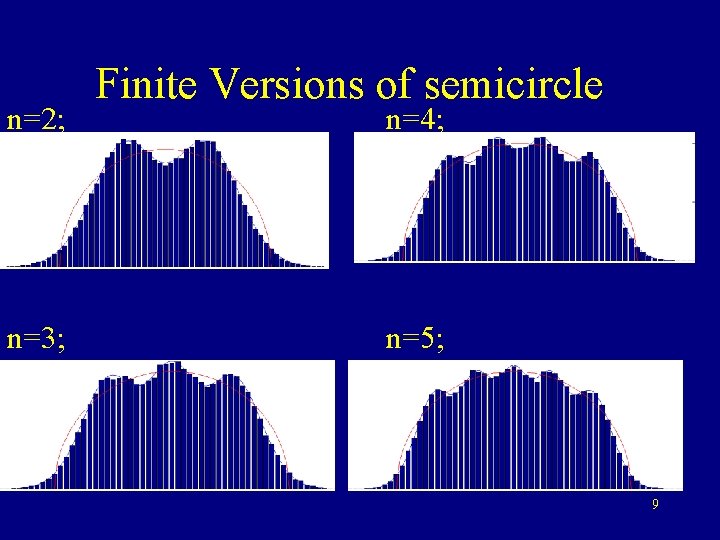
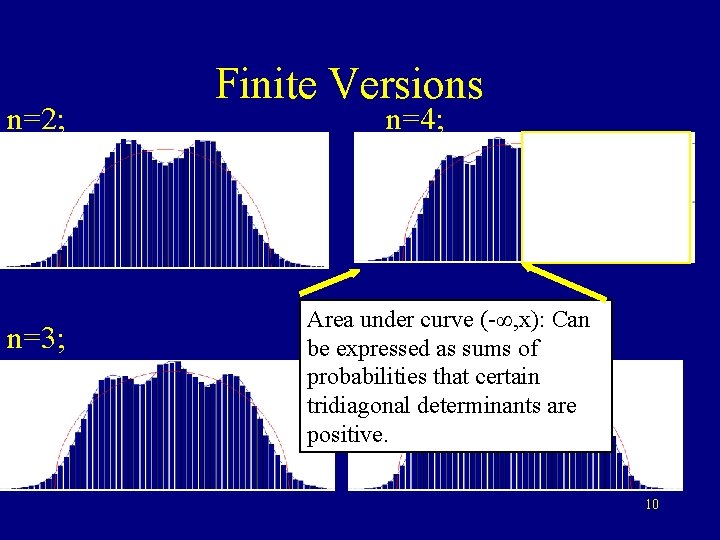
n=2; n=3; Finite Versions of semicircle n=4; n=5; 9

n=2; n=3; Finite Versions n=4; Area under curve (-∞, x): Can n=5; as sums of be expressed probabilities that certain tridiagonal determinants are positive. 10

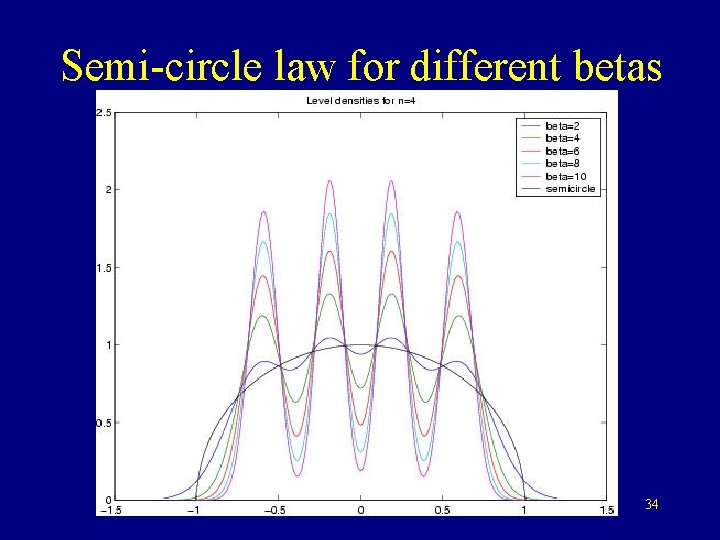
Wigner’s Semi-Circle v Real Numbers: x v Complex Numbers: x+iy v Quaternions: x+iy+jz+kw Defined through joint eigenvalue density: v β=2½? x+iy+jz β const x ∏|xi-xj| ∏exp(-xi 2 /2) β=1 β=2 β=4 β=2½? β=repulsion strength β=0 “no interference” spacings are Poisson Classical research only β=1, 2, 4 missing the link to Poisson, continuous techniques, etc 11

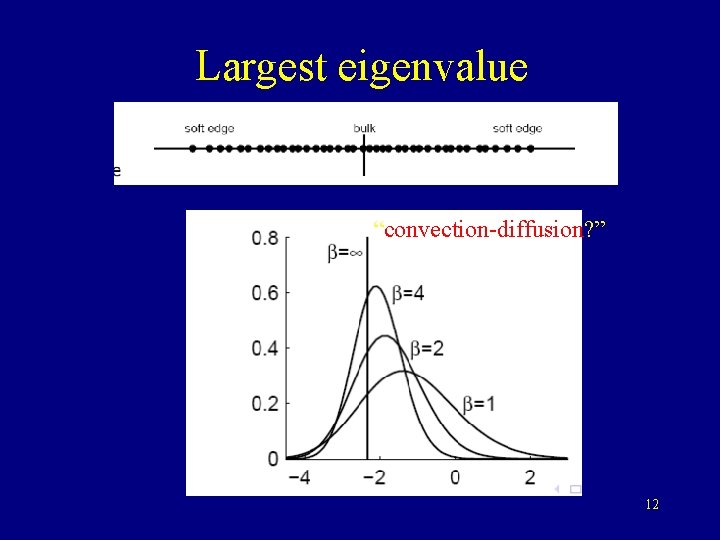
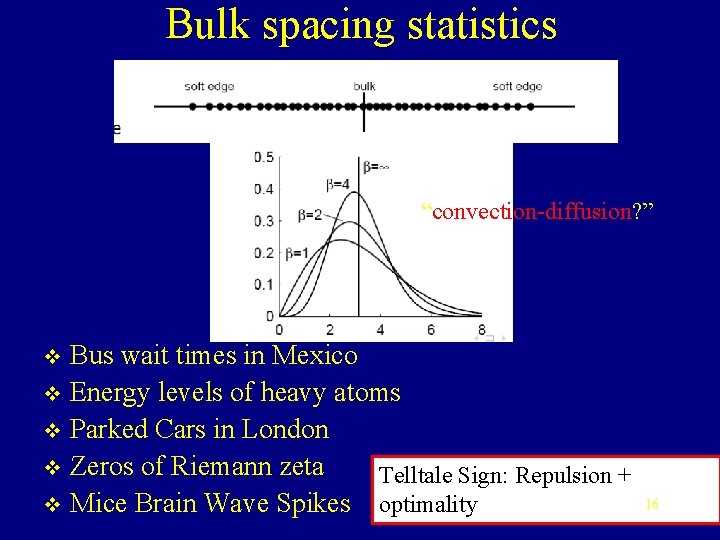
Largest eigenvalue “convection-diffusion? ” 12

Haar or not Haar? “Uniform Distribution on orthogonal matrices” Gram-Schmidt or [Q, R]=QR(randn(n)) 13

Haar or not Haar? “Uniform Distribution on orthogonal matrices” Gram-Schmidt or [Q, R]=QR(randn(n)) Eigenvalues Wrong 14

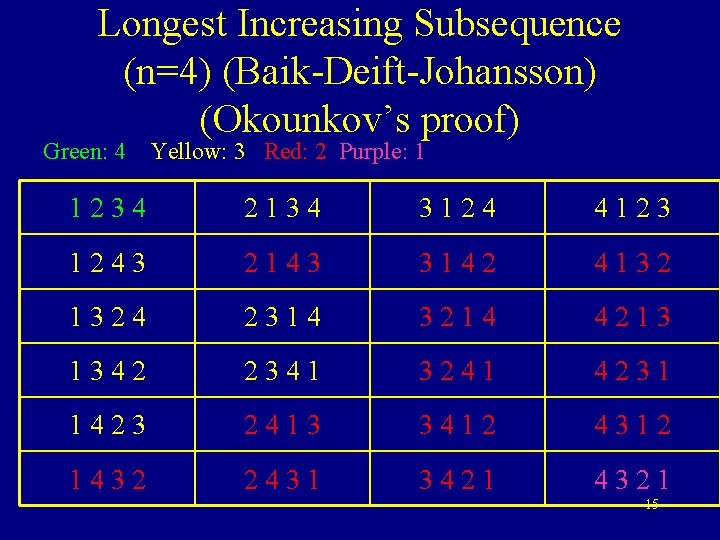
Longest Increasing Subsequence (n=4) (Baik-Deift-Johansson) (Okounkov’s proof) Green: 4 Yellow: 3 Red: 2 Purple: 1 1234 2134 3124 4123 1243 2143 3142 4132 1324 2314 3214 4213 1342 2341 3241 4231 1423 2413 3412 4312 1432 2431 3421 4321 15

Bulk spacing statistics “convection-diffusion? ” Bus wait times in Mexico v Energy levels of heavy atoms v Parked Cars in London v Zeros of Riemann zeta Telltale Sign: Repulsion + v Mice Brain Wave Spikes optimality v 16

“what’s my β? ” web page • • Cy’s tricks: Maximum Likelihood Estimation Bayesian Probability Kernel Density Estimation • Epanechnikov kernel Confidence Intervals http: //people. csail. mit. edu/cychan/Beta. Estimator. html 17

Open Questions v Find new applications of spacing (or other) distributions v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 18

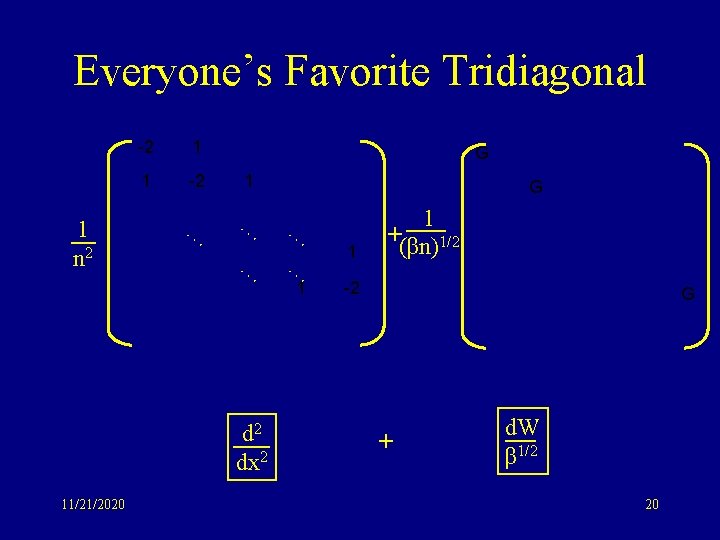
Everyone’s Favorite Tridiagonal 1 n 2 -2 1 1 -2 1 … … … 1 1 -2 d 2 dx 2 11/21/2020 19

Everyone’s Favorite Tridiagonal 1 n 2 -2 1 1 -2 1 … … … 1 1 -2 G d 2 dx 2 11/21/2020 G 1 +(βn)1/2 G + d. W β 1/2 20

Stochastic Operator Limit 2 d - x + 2 dx 2 d. W , β æ N(0, 2) χ (n -1)β ç ç χ (n -1)β N(0, 2) χ (n - 2)β 1 ç … Hβn ~ … ç 2 nβ ç χ 2β ç è H β n » H n + ö ÷ ÷ ÷ … ÷, N(0, 2) χβ ÷ ÷ χβ N(0, 2) ø 2 G β Cast of characters: Dumitriu, Sutton, Rider n , 21

Open Questions v Find new applications of spacing (or other) distributions v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 22

Is it really the random matrices? The excitement is that the random matrix statistics are everyhwere v Random matrices properly tridiagonalized are discretizations of stochastic differential operators! v Eigenvalues of SDO’s not as well studied v Deep down this is what I believe is the important mechanism in the spacings, not the random matrices! (See Brian Sutton thesis, Brian Rider papers—connection to Schrodinger operators) v Deep down for other statistics, though it’s the matrices v 23

Open Questions v Find new applications of spacing (or other) distributions v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 24

Open Questions v Find new applications of spacing (or other) distributions v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 26

Free Probability v Free Probability (name refers to “free algebras” meaning no strings attached) v Gets us past Gaussian ensembles and Wishart Matrices 27

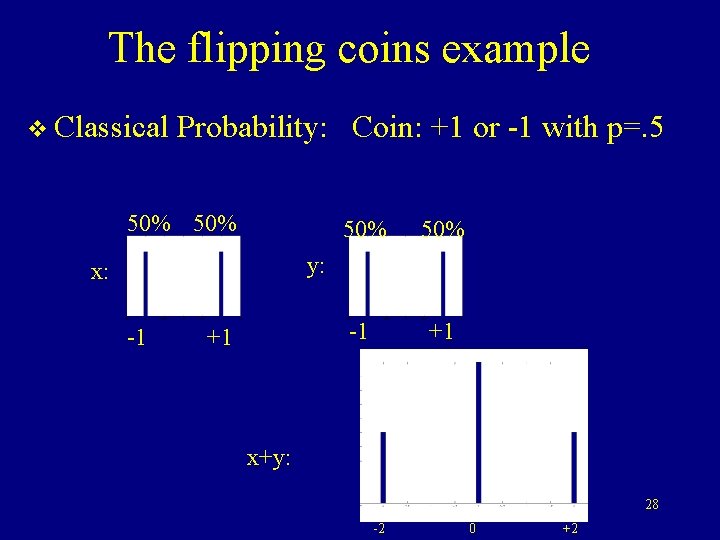
The flipping coins example v Classical Probability: Coin: +1 or -1 with p=. 5 50% 50% -1 +1 y: x: -1 +1 x+y: 28 -2 0 +2

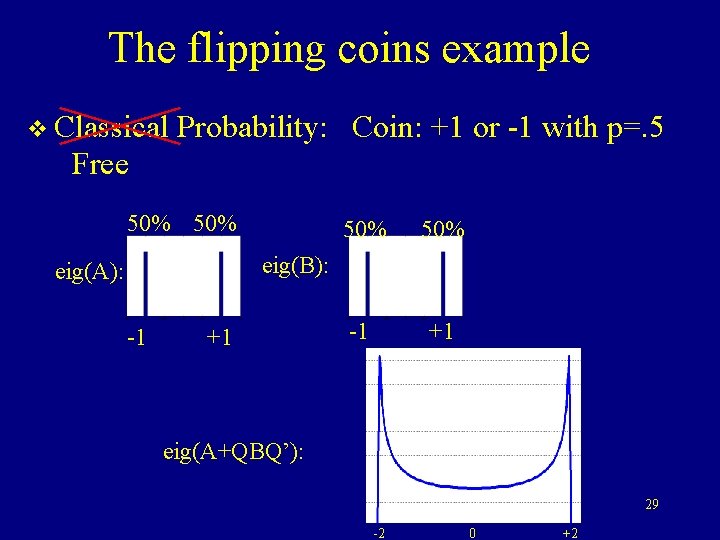
The flipping coins example v Classical Probability: Coin: +1 or -1 with p=. 5 Free 50% 50% -1 +1 eig(B): eig(A): -1 +1 eig(A+QBQ’): 29 -2 0 +2

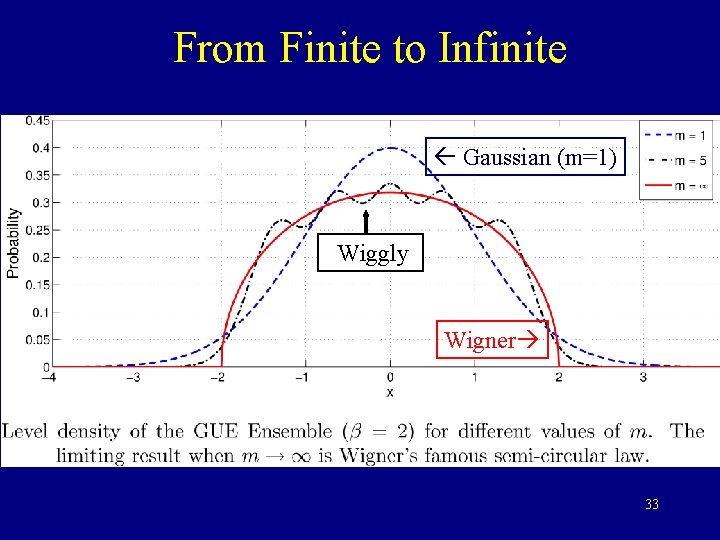
From Finite to Infinite 30

From Finite to Infinite Gaussian (m=1) 31

From Finite to Infinite Gaussian (m=1) Wiggly 32

From Finite to Infinite Gaussian (m=1) Wiggly Wigner 33

Semi-circle law for different betas 34

Open Questions v Find new applications of spacing (or other) distributions v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 35

Matrix Statistics • Many Worked out in 1950 s and 1960 s • Muirhead “Aspects of Multivariate Statistics” • Are two covariance matrices equal? • Does my matrix equal this matrix? • Is my matrix a multiple of the identity? • Answers Require Computation of • Hypergeometrics of Matrix Argument • Long thought Computationally Intractible 36

The special functions of multivariate statistics Hypergeometric Functions of Matrix Argument v β=2: Schur Polynomials v Other values: Jack Polynomials v Orthogonal Polynomials of Matrix Argument v v Begin with w(x) on I v ∫ pκ(x)pλ(x) Δ(x)β ∏i w(xi)dxi = δκλ v Jack Polynomials orthogonal for w=1 Analogs of xm on the unit circle. v Plamen Koev revolutionary computation v Dumitriu’s MOPS symbolic package 37

Multivariate Orthogonal Polynomials & Hypergeometrics of Matrix Argument v The important special functions of the 21 st century v Begin with w(x) on I v∫ pκ(x)pλ(x) Δ(x)β ∏i w(xi)dxi = δκλ v. Jack Polynomials orthogonal for w=1 on the unit circle. Analogs of xm 38

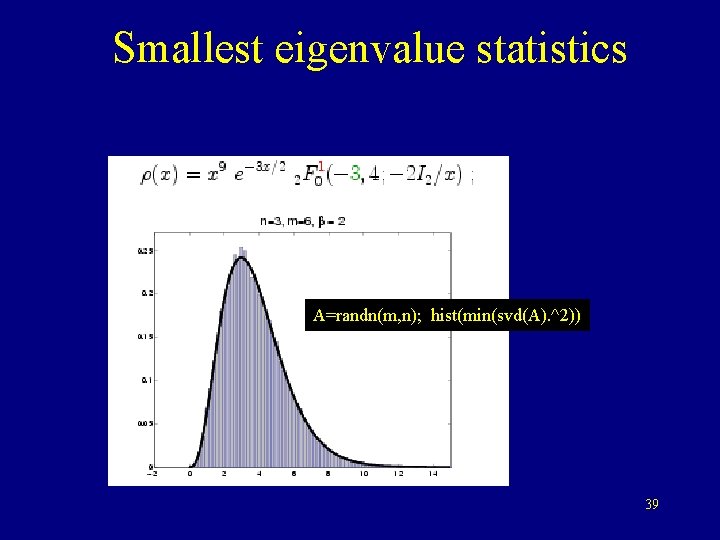
Smallest eigenvalue statistics A=randn(m, n); hist(min(svd(A). ^2)) 39

Multivariate Hypergeometric Functions 40

Multivariate Hypergeometric Functions 41

Open Questions v Find new applications of spacing (or other) distributions v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 42

Plamen Koev’s clever idea 43

Symbolic MOPS applications A=randn(n); S=(A+A’)/2; trace(S^4) det(S^3) 44

Mops (Ioana Dumitriu) Symbolic 45

Random Matrix Calculator 46

Encoding the semicircle The algebraic secret v f(x) = sqrt(4 -x 2)/(2π) v m(z) = (-z + i*sqrt(4 -z 2))/2 v L(m, z) ≡ m 2+zm+1=0 m(z) = ∫ (x-z)-1 f(x) dx Stieltjes transform Practical encoding: Polynomial L whose root m is Stieltjes transform 47

The Polynomial Method v RMTool v http: //arxiv. org/abs/math/0601389 v The polynomial method for random matrices v Eigenvectors as well! 48

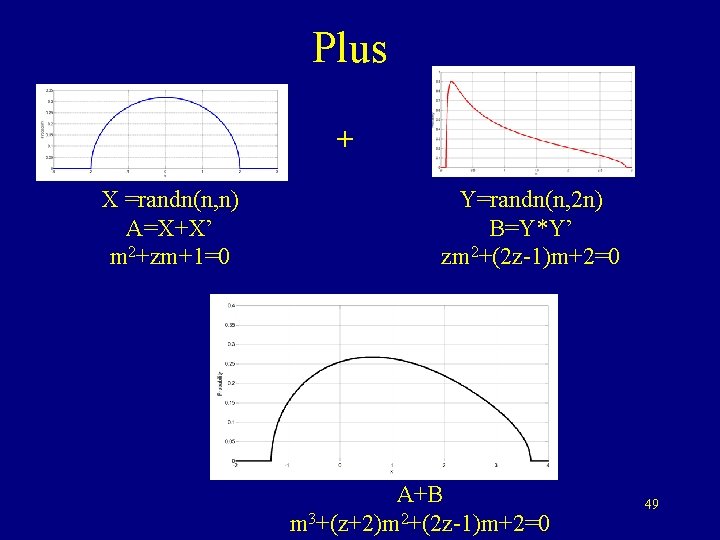
Plus + X =randn(n, n) A=X+X’ m 2+zm+1=0 Y=randn(n, 2 n) B=Y*Y’ zm 2+(2 z-1)m+2=0 A+B m 3+(z+2)m 2+(2 z-1)m+2=0 49

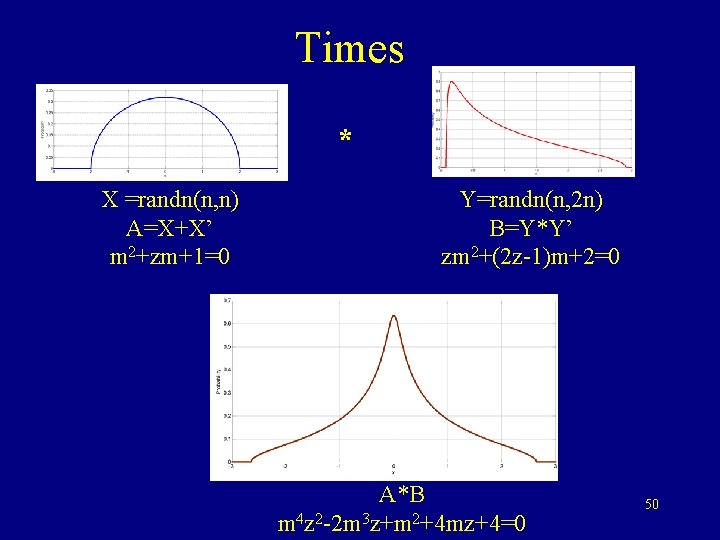
Times * X =randn(n, n) A=X+X’ m 2+zm+1=0 Y=randn(n, 2 n) B=Y*Y’ zm 2+(2 z-1)m+2=0 A*B m 4 z 2 -2 m 3 z+m 2+4 mz+4=0 50

Open Questions v Find new applications of spacing (or other) distributions v Cleanest derivation of Tracy-Widom? v “Finite” free probability? v Finite meets infinite v Muirhead v Software meets Tracy-Widom for stochastic eigen-analysis 51

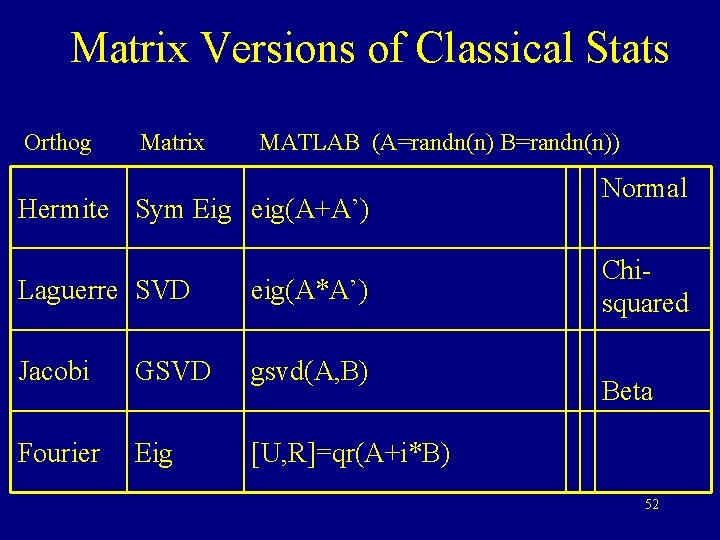
Matrix Versions of Classical Stats Orthog Matrix MATLAB (A=randn(n) B=randn(n)) Hermite Sym Eig eig(A+A’) Laguerre SVD eig(A*A’) Jacobi GSVD gsvd(A, B) Fourier Eig [U, R]=qr(A+i*B) Normal Chisquared Beta 52

The big structure Orthog Matrix Weight Stats Hermite Sym Eig exp(-x 2) Normal Laguerre SVD Jacobi Fourier GSVD Eig xαe-x Chisquared (1 -x)α x Beta β (1+x) eiθ Graph Theory Sym. Space Complete Graph Bipartite Graph noncompact A, AII noncompact AIII, BDI, CII compact Regular Graph A, AII, C, D, CI, D, DIII compact AIII, BDI, 53 CDI

Summary v Stochastic Eigenanalysis v Emerging Techniques v Open Problems 54