Advanced Scaling Techniques for the Modeling of Materials

Advanced Scaling Techniques for the Modeling of Materials Processing Patricio F. Mendez Colorado School of Mines CWJCR

Goals • For people less familiar with scaling – will show scaling is especially helpful for materials processes • For people familiar with scaling – will show a new relationship that permits to automate part of the scaling process • The reasoning applies to almost all materials processes • For clarity, I’ll use a particular welding problem as an example, but the approach is valid beyond welding 2 CWJCR

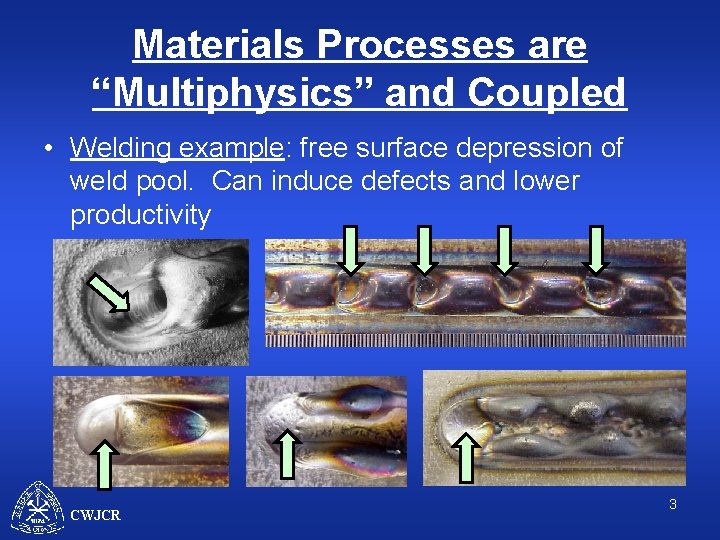
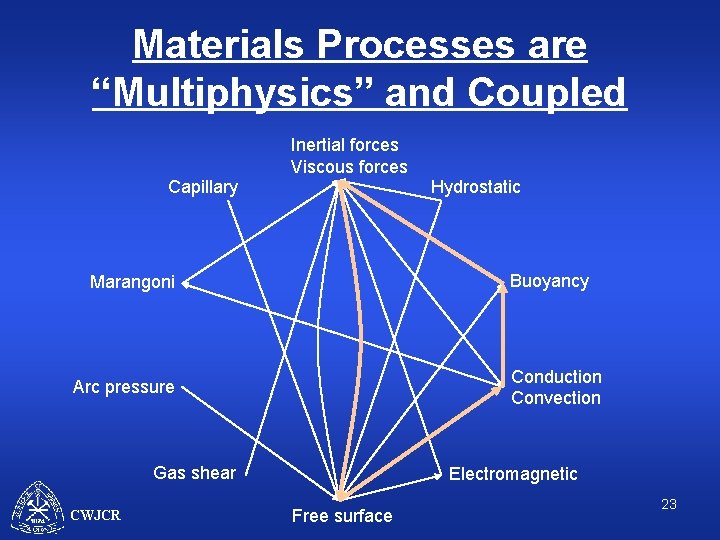
Materials Processes are “Multiphysics” and Coupled • Welding example: free surface depression of weld pool. Can induce defects and lower productivity CWJCR 3

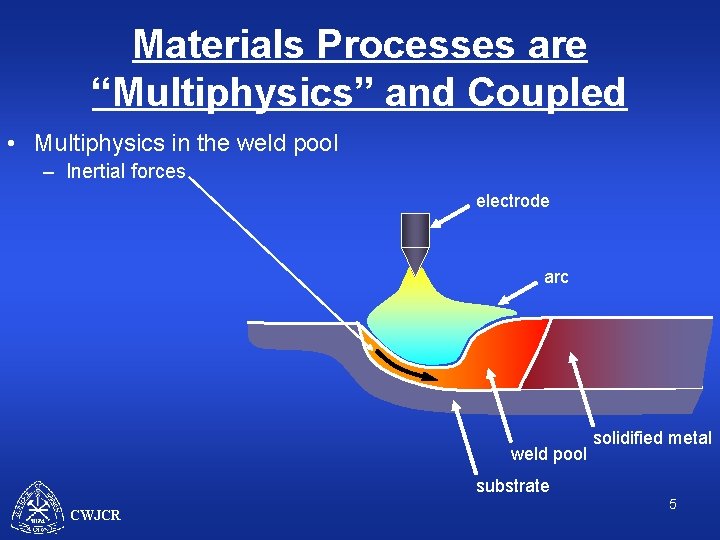
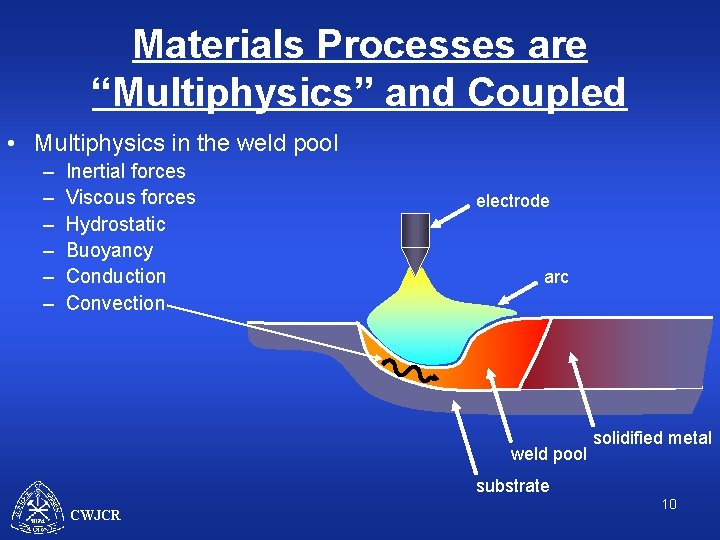
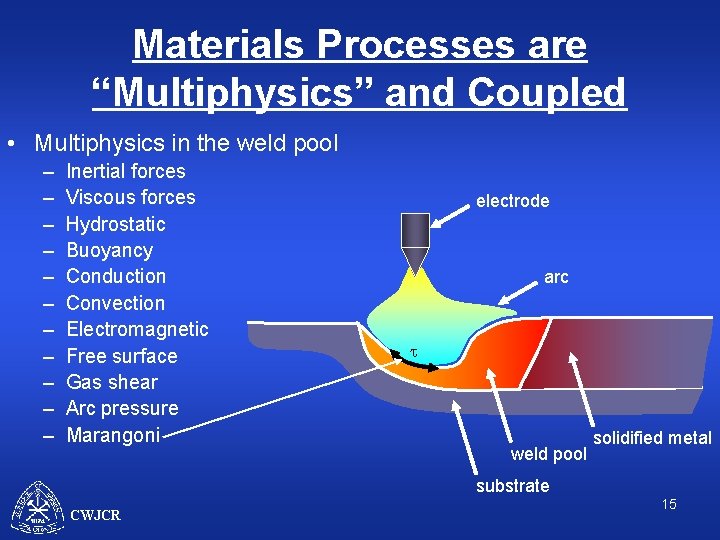
Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool (12) electrode arc weld pool solidified metal substrate CWJCR 4

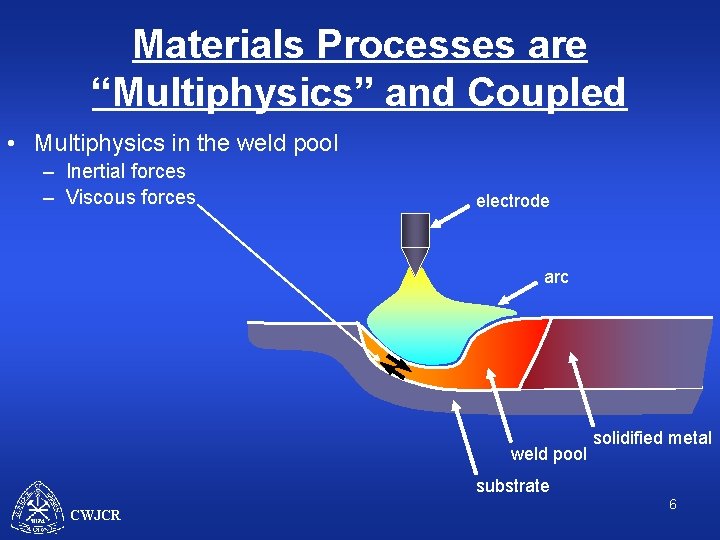
Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – Inertial forces electrode arc weld pool solidified metal substrate CWJCR 5

Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – Inertial forces – Viscous forces electrode arc weld pool solidified metal substrate CWJCR 6

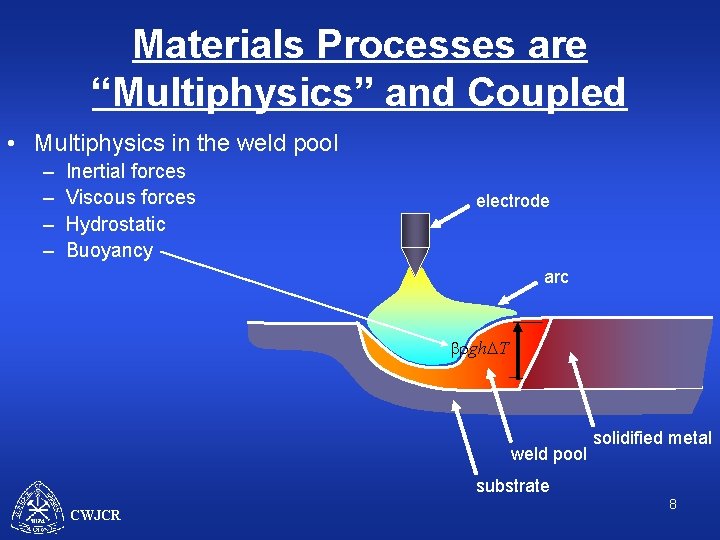
Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – Inertial forces – Viscous forces – Hydrostatic electrode arc rgh weld pool solidified metal substrate CWJCR 7

Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – Inertial forces Viscous forces Hydrostatic Buoyancy electrode arc brgh. DT weld pool solidified metal substrate CWJCR 8

Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction electrode arc weld pool solidified metal substrate CWJCR 9

Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction Convection electrode arc weld pool solidified metal substrate CWJCR 10

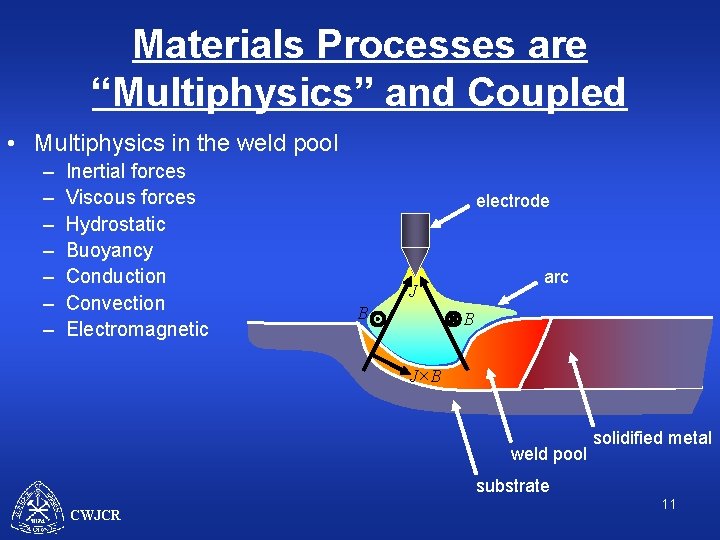
Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction Convection Electromagnetic electrode arc J B B J×B weld pool solidified metal substrate CWJCR 11

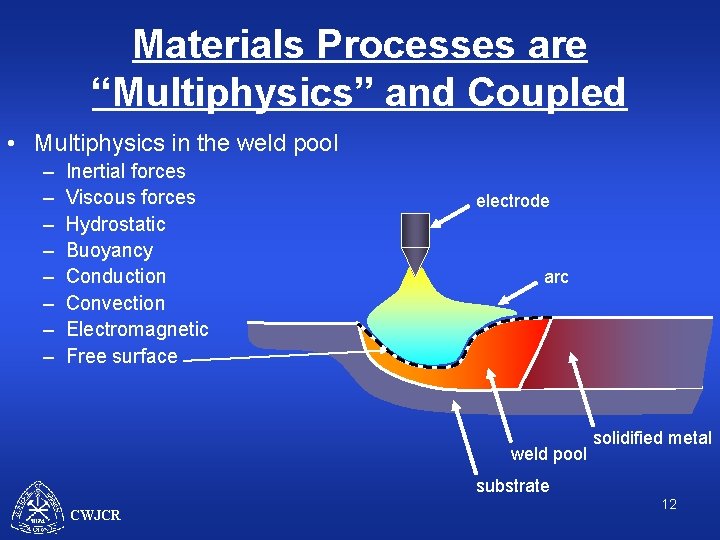
Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction Convection Electromagnetic Free surface electrode arc weld pool solidified metal substrate CWJCR 12

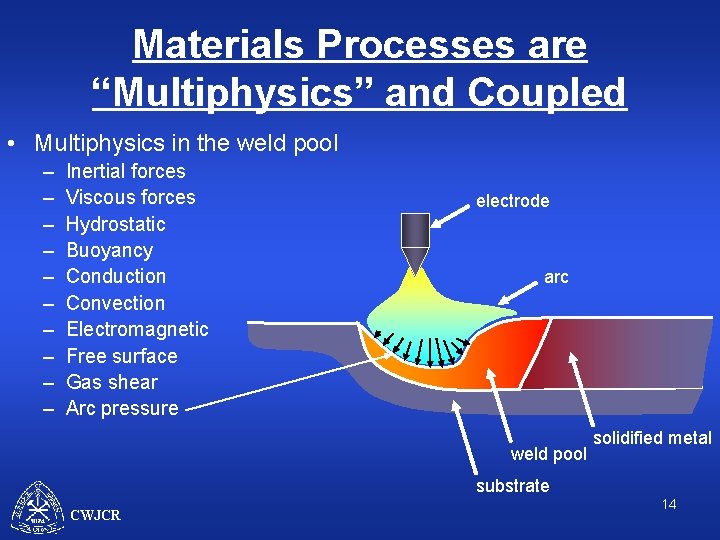
Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction Convection Electromagnetic Free surface Gas shear electrode arc t weld pool solidified metal substrate CWJCR 13

Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction Convection Electromagnetic Free surface Gas shear Arc pressure electrode arc weld pool solidified metal substrate CWJCR 14

Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction Convection Electromagnetic Free surface Gas shear Arc pressure Marangoni electrode arc t weld pool solidified metal substrate CWJCR 15

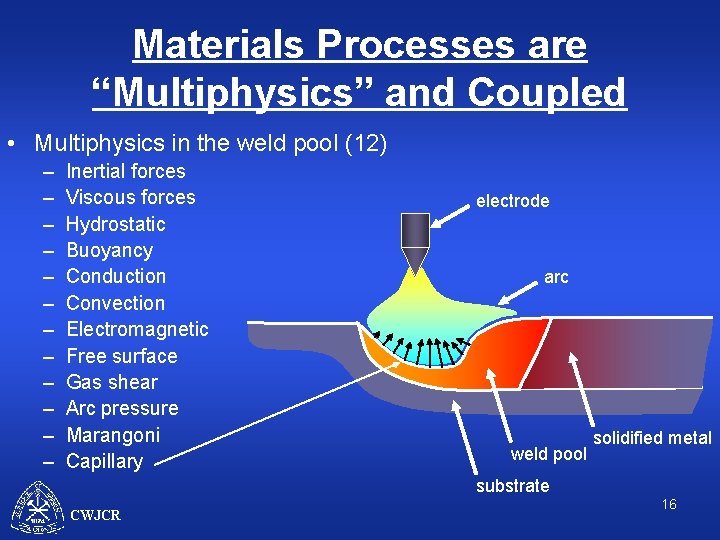
Materials Processes are “Multiphysics” and Coupled • Multiphysics in the weld pool (12) – – – Inertial forces Viscous forces Hydrostatic Buoyancy Conduction Convection Electromagnetic Free surface Gas shear Arc pressure Marangoni Capillary electrode arc weld pool solidified metal substrate CWJCR 16

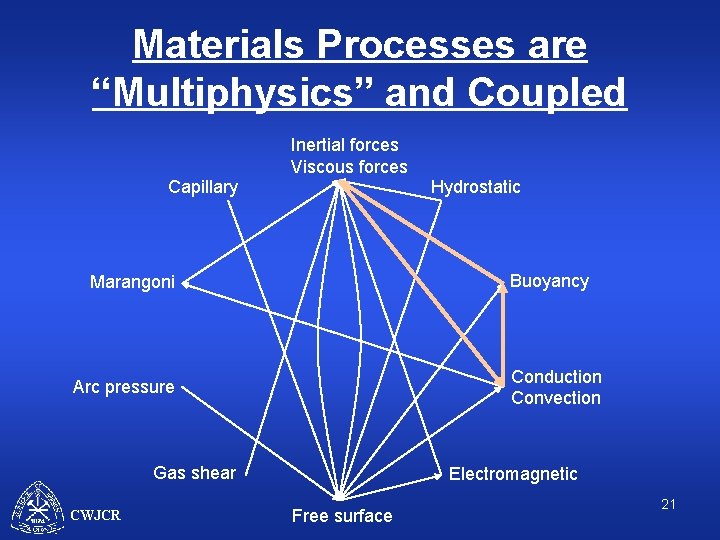
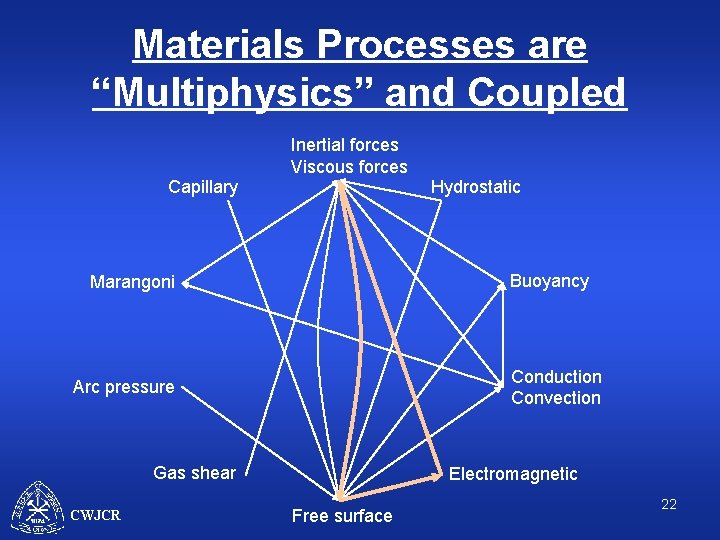
Materials Processes are “Multiphysics” and Coupled Inertial forces Viscous forces Capillary Hydrostatic Buoyancy Marangoni Conduction Convection Arc pressure Gas shear CWJCR Electromagnetic Free surface 17

Materials Processes are “Multiphysics” and Coupled Inertial forces Viscous forces Capillary Hydrostatic Buoyancy Marangoni Conduction Convection Arc pressure Gas shear CWJCR Electromagnetic Free surface 18

Materials Processes are “Multiphysics” and Coupled Inertial forces Viscous forces Capillary Hydrostatic Buoyancy Marangoni Conduction Convection Arc pressure Gas shear CWJCR Electromagnetic Free surface 19

Materials Processes are “Multiphysics” and Coupled Inertial forces Viscous forces Capillary Hydrostatic Buoyancy Marangoni Conduction Convection Arc pressure Gas shear CWJCR Electromagnetic Free surface 20

Materials Processes are “Multiphysics” and Coupled Inertial forces Viscous forces Capillary Hydrostatic Buoyancy Marangoni Conduction Convection Arc pressure Gas shear CWJCR Electromagnetic Free surface 21

Materials Processes are “Multiphysics” and Coupled Inertial forces Viscous forces Capillary Hydrostatic Buoyancy Marangoni Conduction Convection Arc pressure Gas shear CWJCR Electromagnetic Free surface 22

Materials Processes are “Multiphysics” and Coupled Inertial forces Viscous forces Capillary Hydrostatic Buoyancy Marangoni Conduction Convection Arc pressure Gas shear CWJCR Electromagnetic Free surface 23

Disagreement about dominant mechanism • Experiments cannot show under the surface • Numerical simulations have convergence problems with a very deformed free surface Proposed explanations for very deformed weld pool • Ishizaki (1980): gas shear, experimental • Oreper (1983): Marangoni, numerical • Lin (1985): vortex, analytical • Choo (1991): Arc pressure, gas shear, numerical • Rokhlin (1993): electromagnetic, hydrodynamic, experimental • Weiss (1996): arc pressure, numerical CWJCR 24

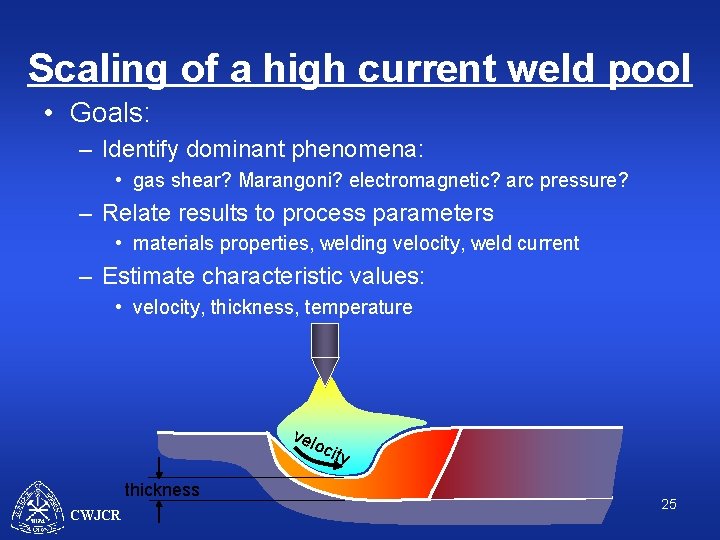
Scaling of a high current weld pool • Goals: – Identify dominant phenomena: • gas shear? Marangoni? electromagnetic? arc pressure? – Relate results to process parameters • materials properties, welding velocity, weld current – Estimate characteristic values: • velocity, thickness, temperature vel oci ty thickness CWJCR 25

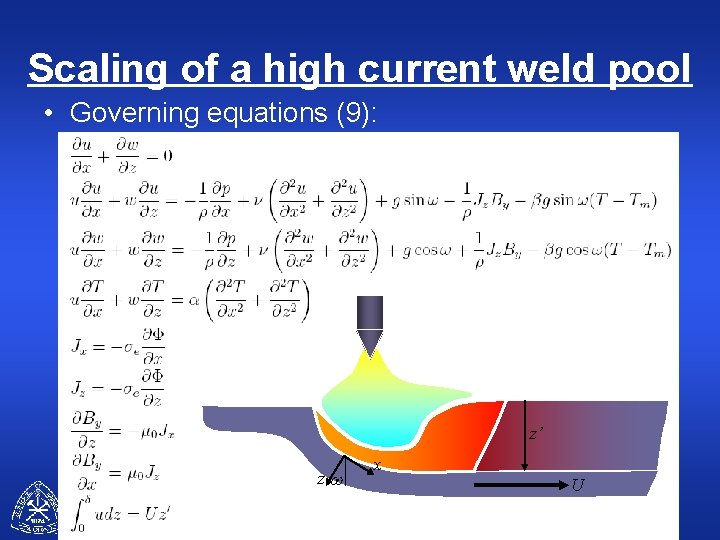
Scaling of a high current weld pool • Governing equations (9): z’ zw CWJCR x U 26

Scaling of a high current weld pool • Boundary Conditions: at free surface at solid-melt interface far from weld free surface CWJCR solid-melt interface far from weld 27

Scaling of a high current weld pool • Variables and Parameters – independent variables (2) – dependent variables (9) – parameters (18) with so many parameters Dimensional Analysis is not effective from other models, experiments CWJCR 28

Classical Scaling Approach 1. 2. 3. 4. 5. 6. Scale variables and differential expressions Assume a set of dominant driving forces Normalize equations Solve for the unknown terms Verify self-consistency If not self-consistent, return to 3. Roughly, this is the approach suggested by Dantzig and Tucker, Bejan, Kline, Denn, Deen, Sides, Chen, Astarita, and more CWJCR 29

Classical Scaling Approach unknown characteristic values (9): CWJCR 30

Classical Scaling Approach governing equation CWJCR 31

Classical Scaling Approach governing equation scaled variables OM(1) CWJCR 32

Classical Scaling Approach governing equation scaled variables normalized equation output CWJCR input OM(1) input 33

Classical Scaling Approach two possible balances B 1 output CWJCR input 34

Classical Scaling Approach two possible balances output CWJCR B 1 B 2 input 35

Classical Scaling Approach two possible balances balance B 1 generates one algebraic equation: output CWJCR B 1 B 2 input 36

Classical Scaling Approach two possible balances balance B 1 generates one algebraic equation: balance B 2 generates a different equation: output CWJCR B 1 B 2 input 37

Classical Scaling Approach two possible balances balance B 1 generates one algebraic equation: balance B 2 generates a different equation: self-consistency: choose the balance that makes the neglected term less than 1 output CWJCR B 1 B 2 input 38

Classical Scaling Approach two possible balances balance B 1 generates one algebraic equation: balance B 2 generates a different equation: self-consistency: choose the balance that makes the neglected term less than 1 TWO BIG PROBLEMS FOR MATERIALS PROCESSES! CWJCR 39

Classical Scaling Approach ? two possible balances 1 equation 2 unknowns balance B 1 generates one algebraic equation: ? balance B 2 generates a different equation: ? ? ? 1 equation 3 unknowns self-consistency: choose the balance that makes the neglected term less than 1 TWO BIG PROBLEMS FOR MATERIALS PROCESSES! 1. Each balance equation involves more than one unknown CWJCR 40

Classical Scaling Approach two possible balances balance B 1 generates one algebraic equation: balance B 2 generates a different equation: self-consistency: choose the balance that makes the neglected term less than 1 TWO BIG PROBLEMS FOR MATERIALS PROCESSES! 1. Each balance equation involves more than one unknown 2. A system of equations involves many thousands of possible balances CWJCR 41

Scaled equations (9) all coefficients are power laws all terms in parenthesis expected to be OM(1) CWJCR 42

Scaled BCs (6) Boundary conditions CWJCR 43

Iterative process • Simple scaling approach involves 334098 possible combinations • There are 116 self-consistent solutions – there is no unicity of solution – we cannot stop at first self-consistent solution – self-consistent solutions are grouped into 55 classes (1 - 6 solutions per class) CWJCR 44

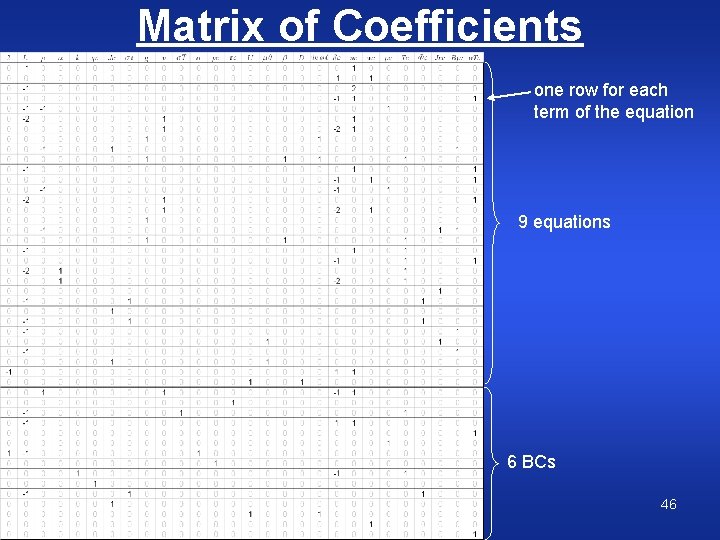
Automating iterative process • Power-law coefficients can be transformed into linear expressions using logarithms • Several power law equations can then be transformed into a linear system of equations • Normalizing an equation consists of subtracting rows CWJCR 45

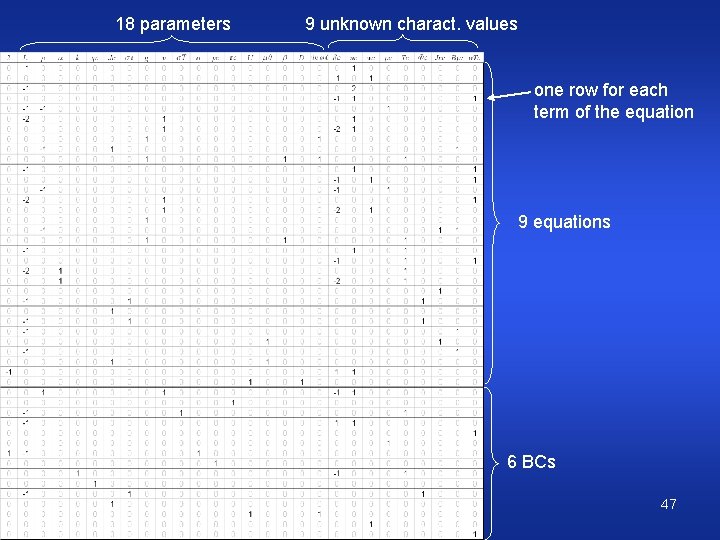
Matrix of Coefficients one row for each term of the equation 9 equations 6 BCs CWJCR 46

18 parameters 9 unknown charact. values one row for each term of the equation 9 equations 6 BCs CWJCR 47

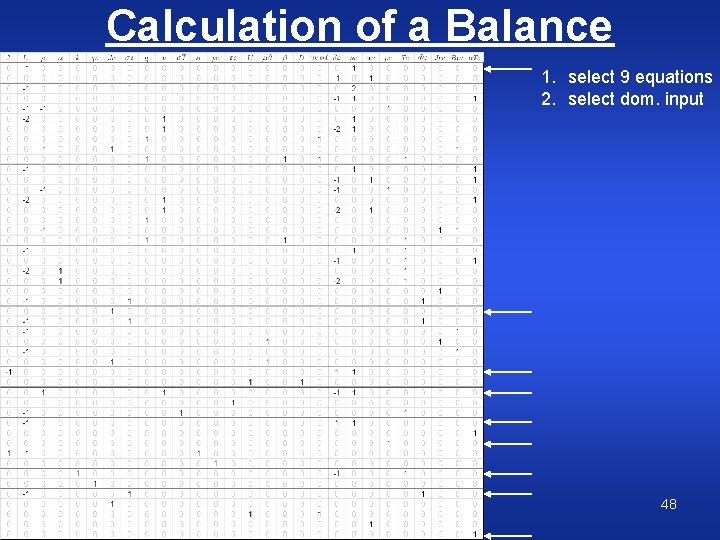
Calculation of a Balance 1. select 9 equations 2. select dom. input CWJCR 48

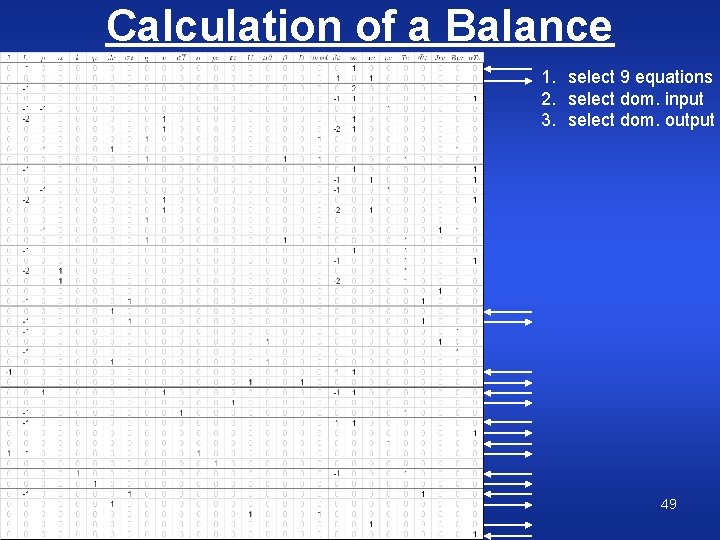
Calculation of a Balance 1. select 9 equations 2. select dom. input 3. select dom. output CWJCR 49

Calculation of a Balance 1. 2. 3. 4. 18 parameters CWJCR [No]P’ select 9 equations select dom. input select dom. output build submatrix of selected normalized outputs 9 unknown charact. values [No]S 9 x 9 50

Calculation of a Balance 18 parameters CWJCR [No]P’ 9 unknown charact. values [No]S 9 x 9 51

Calculation of a Balance 18 parameters CWJCR [No]P’ 9 unknown charact. values [No]S 9 x 9 52

Calculation of a Balance incompatible power law estimation 18 parameters CWJCR [No]P’ 9 unknown charact. values [No]S 9 x 9 53

Calculation of a Balance incompatible power law estimation Matrix [S] 9 unknowns CWJCR 18 parameters 54

Calculation of a Balance Matrix [S] 9 unknowns CWJCR 18 parameters 55

Self consistency • can be checked using matrix approach secondary terms submatrices of normalized secondary terms • checking the 334098 combinations took 72 seconds using Matlab on a Pentium M 1. 4 GHz CWJCR 56

Scaling results Tc Uc CWJCR dc=36 mm dc 57

CWJCR diff. =/diff. ^ buoyancy / viscous Marangoni / gas shear capillary / viscous hydrostatic / viscous electromagnetic / viscous arc pressure / viscous convection / conduction inertial / viscous gas shear / viscous Scaling results plasma shear causes crater 58

Summary • Materials processes are “Multiphysics” and “Multicoupled” • Scaling helps understand the dominant forces in materials processes • Several thousand iterations are necessary for scaling • The “Matrix of Coefficients” and associate matrix relationships help automate scaling CWJCR 59

CWJCR 60

Approaches to the high current weld pool problem • Experimental Ishizaki, 1962, 1980. Hammer blow, water droplets. Savage 1978, blank shot Force Balance: Lin and Eagar, 1985 Savage, 1979 Adonyi, 1992 Shimada, 1982 CWJCR very depressed weld pool become a “film” … and many more 61

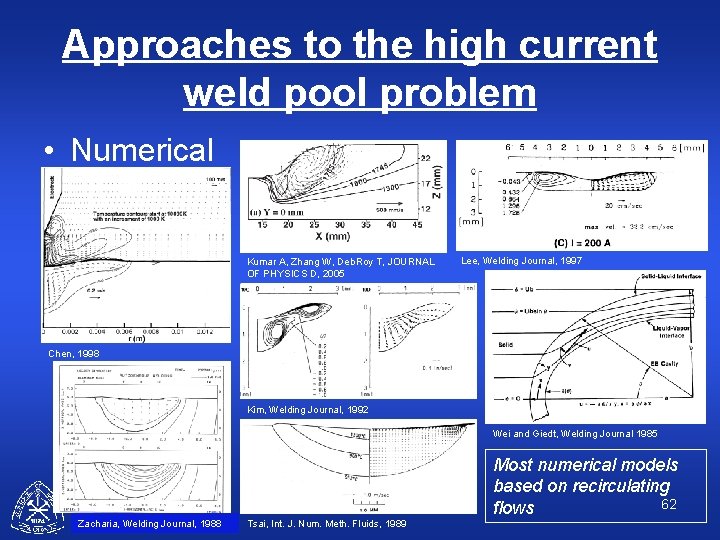
Approaches to the high current weld pool problem • Numerical Kumar A, Zhang W, Deb. Roy T, JOURNAL OF PHYSICS D, 2005 Lee, Welding Journal, 1997 Chen, 1998 Kim, Welding Journal, 1992 Wei and Giedt, Welding Journal 1985 CWJCR Zacharia, Welding Journal, 1988 Most numerical models based on recirculating 62 flows Tsai, Int. J. Num. Meth. Fluids, 1989

Approaches to the high current weld pool problem • Scaling: Focused on recirculating flows Oreper & Szekely, J. Fluid Mech. 1984, TWR 1986 Deb. Roy & David Rev. Modern Phys 1995 Rivas & Ostrach, Int. J. Heat Mass Transfer 1992 Chakraborty & Dutta STWJ, 1992 No velocity BL No thermal BL Velocity BL Thermal BL CWJCR DT, R, D come from numerical DT comes from scaling, R, D from calculations, experiments 63 numerical calculations, experiments