Advanced Programming Techniques Divide and Conquer Dynamic Programming



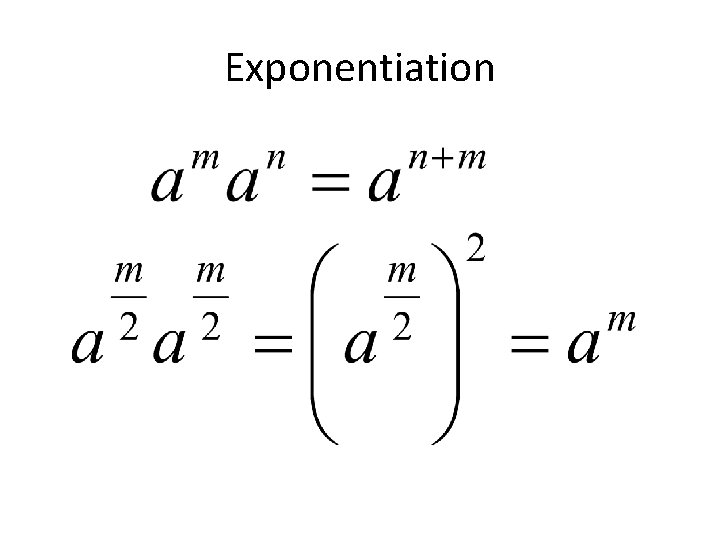
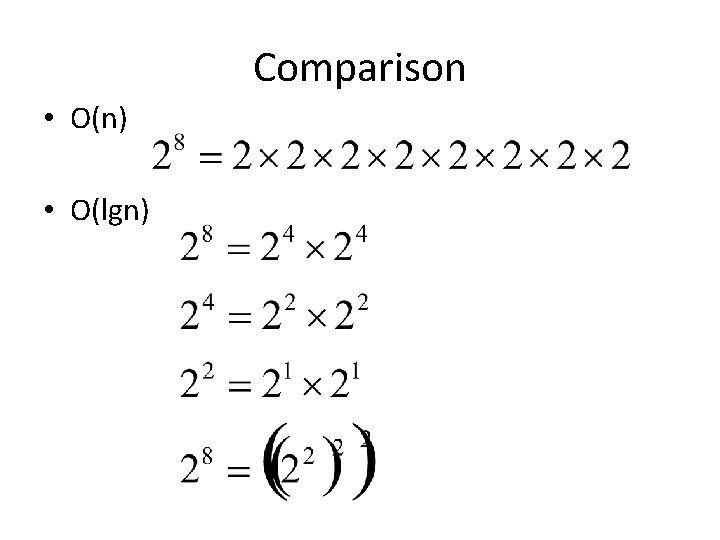




![Enter Dynamic Programming public int pow(int b, int e) { int[] solved = new Enter Dynamic Programming public int pow(int b, int e) { int[] solved = new](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-12.jpg)


![Fibonacci Memoization public int fib(int n) { int[] sub. Probs = new int[n+1]; return Fibonacci Memoization public int fib(int n) { int[] sub. Probs = new int[n+1]; return](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-17.jpg)


![Fibonacci Bottom Up public static int fib(int n) { int[] solns = new int[n+1]; Fibonacci Bottom Up public static int fib(int n) { int[] solns = new int[n+1];](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-20.jpg)






![Dynamic Programming public int pascal(int r, int c, int[][] solved) { if(r == c Dynamic Programming public int pascal(int r, int c, int[][] solved) { if(r == c](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-28.jpg)


![LIS(n) public int incr. Sub(int[] list, int n) { if(n == list. length - LIS(n) public int incr. Sub(int[] list, int n) { if(n == list. length -](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-31.jpg)
![public int lis(int[] list) { int longest = 1; for(int n = 0; n public int lis(int[] list) { int longest = 1; for(int n = 0; n](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-32.jpg)

![public static int lis. DP(int[] list) { int longest = 1; int[] solutions = public static int lis. DP(int[] list) { int longest = 1; int[] solutions =](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-34.jpg)


- Slides: 36

Advanced Programming Techniques • Divide and Conquer • Dynamic Programming

Divide and Conquer • You’ve already done this… – Binary search – Merge sort – Quicksort

Exponentiation • Brute force O(n): public int pow(int b, int e) { int result = 1; for(int n = 0; n < e; n++) result *= b; return result; }
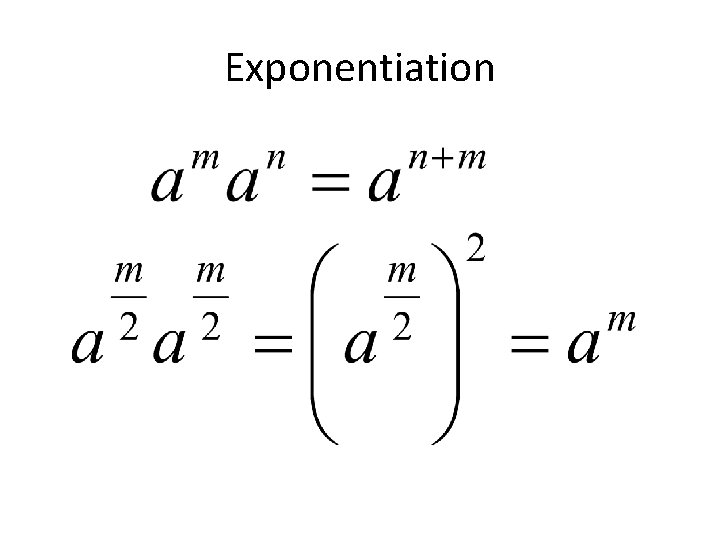
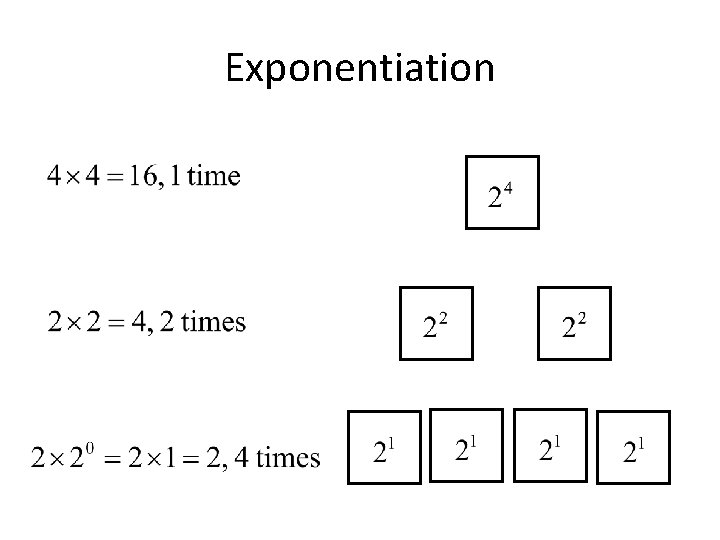
Exponentiation
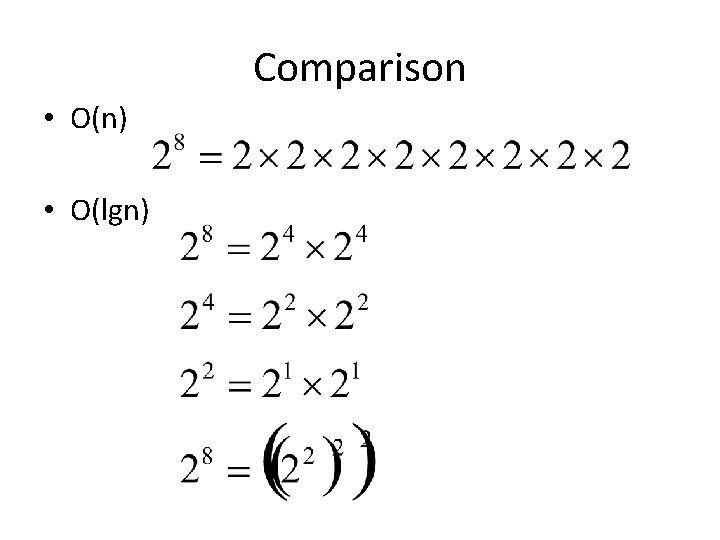
Comparison • O(n) • O(lgn)
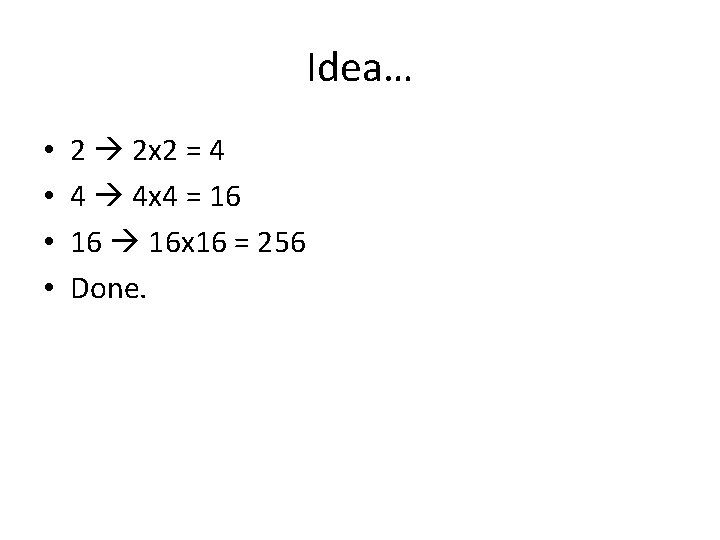
Idea… • • 2 2 x 2 = 4 4 4 x 4 = 16 16 16 x 16 = 256 Done.

Exponentiation - recursive public int pow(int b, int e) { if(e == 0) return 1; } else if(e % 2 == 0) return pow(b, e/2) * pow(b, e/2); else//odd return b * pow(b, e-1); //even

Exponentiation - loop public int pow(int b, int e) { int result = 1; while(e > 0) { if(e % 2 == 1)//odd result = result * b; e /= 2; b *= b; } } return result;

Dynamic Programming • In a divide and conquer strategy sub problems are non overlapping – binary search – Quicksort • What about problems where sub problems “share” sub problems? – Divide and conquer is inefficient in solving the shared problems more than once

Exponentiation – not so good… public int pow(int b, int e) { if(e == 0) return 1; else if(e%2 == 0) return pow(b, e/2) * pow(b, e/2); else return b*pow(b, e-1); }

Exponentiation
![Enter Dynamic Programming public int powint b int e int solved new Enter Dynamic Programming public int pow(int b, int e) { int[] solved = new](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-12.jpg)
Enter Dynamic Programming public int pow(int b, int e) { int[] solved = new int[e+1]; return pow. DP(b, e, solved); } public int pow. DP(int b, int e, int[] solved) { if(e == 0) solved[e] = 1; else if(solved[e] == 0) { if(e%2 == 0) solved[e] = pow. DP(b, e/2, solved) * pow. DP(b, e/2, solved); else solved[e] = b * pow. DP(b, e-1, solved); } return solved[e]; }

Fibonacci • Consider the recursive solution to the Fibonacci numbers: public int fib(int n) { if(n == 0 || n == 1) return 1; else return fib(n-1) + fib(n-2); }

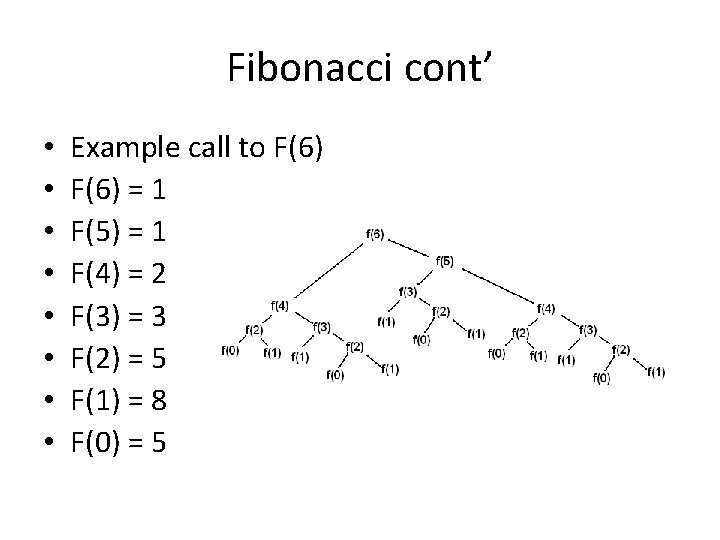
Fibonacci cont’ • • Example call to F(6) = 1 F(5) = 1 F(4) = 2 F(3) = 3 F(2) = 5 F(1) = 8 F(0) = 5

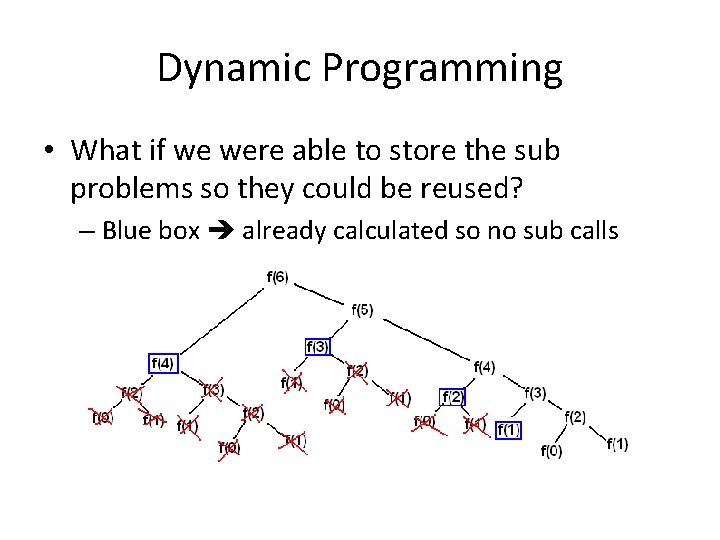
Dynamic Programming • What if we were able to store the sub problems so they could be reused? – Blue box already calculated so no sub calls

Top Down - Memoization • One approach to using dynamic programming is known as memoization – It mimics the idea of “saving” already solved sub problems • You will need to think ahead as to how many sub problems you may need to solve
![Fibonacci Memoization public int fibint n int sub Probs new intn1 return Fibonacci Memoization public int fib(int n) { int[] sub. Probs = new int[n+1]; return](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-17.jpg)
Fibonacci Memoization public int fib(int n) { int[] sub. Probs = new int[n+1]; return fib. Helper(sub. Probs, n); } public int fib. Helper(int[] subs, int n) { if(n == 0 || n == 1) subs[n] = 1; else if(subs[n] == 0) subs[n] = fib. Helper (subs, n - 1) + fib. Helper (subs, n - 2); } return subs[n];

Fibonacci Run • http: //www. pythontutor. com/java. html#code=public+class+Your. Class. Na me. Here+%7 B%0 A++public+static+int+fib(int+n%29%0 A++%7 B%0 A++%09 i nt%5 B%5 D+sub. Probs+%3 D+new+int%5 Bn%2 B 1%5 D%3 B%0 A++%09 return +fib. Helper(sub. Probs, +n%29%3 B%0 A++%7 D%0 A%0 A++public+static+int+fi b. Helper(int%5 B%5 D+subs, +int+n%29%0 A++%7 B%0 A++%09 if(n+%3 D%3 D+ 0+%7 C%7 C+n+%3 D%3 D+1%29%0 A++%09%09 subs%5 Bn%5 D+%3 D+1%3 B %0 A+++%09 else+if(subs%5 Bn 1%5 D+%3 E+0%29%0 A+++%09++subs%5 Bn%5 D+%3 D+subs%5 Bn 1%5 D+%2 B+subs%5 Bn 2%5 D%3 B%0 A+++%09 else%0 A++%09%09 subs%5 Bn%5 D+%3 D+fib. Helper(s ubs, +n+-+1%29+%2 B+fib. Helper(subs, +n++2%29%3 B%0 A++%09 return+subs%5 Bn%5 D%3 B%0 A++%7 D%0 A%0 A++++public+static+void+main(String%5 B%5 D+args%29+%7 B%0 A++++++S ystem. out. println(fib(6%29%29%3 B%0 A++++%7 D%0 A%7 D&mode=edit&o rigin=optfrontend. js&cumulative=false&heap. Primitives=false&text. References=fals e&py=java&raw. Input. Lst. JSON=%5 B%5 D

Bottom Up - Dynamic Programming • In bottom up dynamic programming we build up the sub problems until we reach the problem at hand • One major advantage is the possibility to remove recursion (and sometimes the memory required for memorization)
![Fibonacci Bottom Up public static int fibint n int solns new intn1 Fibonacci Bottom Up public static int fib(int n) { int[] solns = new int[n+1];](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-20.jpg)
Fibonacci Bottom Up public static int fib(int n) { int[] solns = new int[n+1]; solns[0] = 1; solns[1] = 1; for(int k = 2; k <= n; k++) solns[k] = solns[k-1] + solns[k-2]; } return solns[n];

Fibonacci - Final public static int fib(int n) { int f 0 = 1; int fn = 1; for(int k = 2; k <= n; k++) fn = fn + f 0; } return fn;

Dynamic Programming • Like Divide and Conquer and Recursive thinking, you need to practice • The comfortable you are with DP, the more likely you are to recognize it when solving a problem • The big hint here is that sub problems overlap AND contribute to the optimal solution of the given problem – F(5) requires F(4) and F(3) which overlap

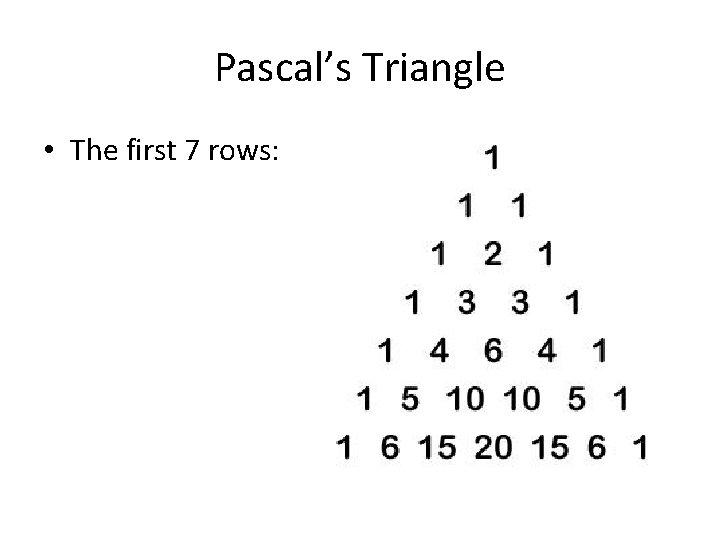
Pascal’s Triangle • The first 7 rows:

Pascal’s Triangle • Recursive definition:

Programmer’s View 0 1 2 3 4 5 0 1 1 2 1 3 1 3 3 1 4 6 4 1 5 10 10 5 1 6 15 20 15 6 • Recursive definition: – P(n, n) = 1 – P(n, 0) = 1 – P(n, m) = P(n-1, m) + P(n-1, m-1) 6 1

Recursion public int pascal(int r, int c) { if(r == c || c == 0) return 1; else return pascal(r – 1, c) + pascal(r – 1, c – 1); }

We’re better than that… • A simple loop is possible but… let’s look at how we can refine the problem using dynamic programming • P(4, 2) P(3, 2) + P(3, 1) – P(3, 2) P(2, 2) + P(2, 1) – P(3, 1) P(2, 1) + P(2, 0) • P(2, 2) 1 • P(2, 1) P(1, 1) + P(1, 0) • P(2, 0) 1 – P(1, 1) 1 – P(1, 0) 1
![Dynamic Programming public int pascalint r int c int solved ifr c Dynamic Programming public int pascal(int r, int c, int[][] solved) { if(r == c](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-28.jpg)
Dynamic Programming public int pascal(int r, int c, int[][] solved) { if(r == c || c == 0) solved[r][c] = 1; else if(solved[r][c] == 0) { solved[r][c] = pascal(r-1, c, solved) + pascal(r-1, c-1, solved); } return solved[r][c]; } *Note: a 2 D array is expensive! There are better ways if you know more math

Longest Increasing Subsequence • {7, 3, 4, 2, 1, 9, 6, 8} • How would you program a computer to find the length of the longest increasing subsequence? – {3, 4, 6, 8} = 4

Brute Force • The LIS can be taken from any starting point in the array • Write a method, LIS(n) to find the LIS from a given starting point, n • Write a loop to look at every possible LIS(n) and return the largest
![LISn public int incr Subint list int n ifn list length LIS(n) public int incr. Sub(int[] list, int n) { if(n == list. length -](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-31.jpg)
LIS(n) public int incr. Sub(int[] list, int n) { if(n == list. length - 1) return 1; else { int max = 1; //LIS of a non-empty list is 1 for(int i = n+1; i < list. length; i++)//search all possible elements after given one { if(list[n] < list[i])//can join this element to subsequence { int temp = 1 + incr. Sub(list, i); if(temp > max) max = temp; } } return max; } }
![public int lisint list int longest 1 forint n 0 n public int lis(int[] list) { int longest = 1; for(int n = 0; n](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-32.jpg)
public int lis(int[] list) { int longest = 1; for(int n = 0; n < list. length; n++) { int temp = incr. Sub(list, n); if(temp > longest) longest = temp; } return longest; } LIS public int incr. Sub(int[] list, int n) { if(n == list. length - 1) return 1; else { int max = 1; //LIS of a non-empty list is 1 for(int i = n+1; i < list. length; i++)//search all possible elements after given one { if(list[n] < list[i])//can join this element to subsequence { int temp = 1 + incr. Sub(list, i); if(temp > max) max = temp; } } return max; } }

LIS - revised • Brute force = O(n^3) • Can you find where dynamic programming would apply here? • {7, 3, 4, 2, 1, 9, 6, 8} – LIS(0) calls LIS(5) – LIS(1) calls LIS(2), LIS(5), LIS(6), LIS(7) – Let’s save each of these calls as we find them
![public static int lis DPint list int longest 1 int solutions public static int lis. DP(int[] list) { int longest = 1; int[] solutions =](https://slidetodoc.com/presentation_image_h2/9f6f619097eec76857f1d0a8deffad49/image-34.jpg)
public static int lis. DP(int[] list) { int longest = 1; int[] solutions = new int[list. length]; for(int n = 0; n < list. length; n++) { int temp = incr. Sub. DP(list, n, solutions); if(temp > longest) longest = temp; } return longest; } public static int incr. Sub. DP(int[] list, int n, int[] longest ) { if(n == list. length - 1) longest[n] = 1; else if(longest[n] == 0) { int max = 1; //LIS of a non-empty list is 1 for(int i = n+1; i < list. length; i++)//search all possible elements after given one { if(list[n] < list[i])//can join this element to subsequence { longest[i] = incr. Sub. DP(list, i, longest); int temp = 1 + longest[i]; if(temp > max) max = temp; } } longest[n] = max; } } return longest[n];

Exercises • This unit is a little bit different from the rest… • You will choose your own problems to solve – Choose 3 problems from the internet that use dynamic programming – Choose 2 CCC contest problems that use dynamic programming • In this case I’m not necessarily looking to see an original solution but for you to demonstrate your understanding of how to solve it using dynamic programming. • Learn from the solutions described on the internet, do not use the corresponding code – If you understand the problem and solution you should be able to program your own code • To do this you will teach me how to apply dynamic programming to solve your chosen problems. – I should see sample problems illustrating how the problem works (simple hand traced ones) – You should explain it to me so I can understand how you used dynamic programming

Contest Practice • Complete 5 additional CCC problems online – They must be from S 3 or higher • Register online – http: //cemc. uwaterloo. ca/contests/computing/co mputing-grader. html – JH = 090602110