Advanced Placement Calculus AB Introduction to Slope Fields

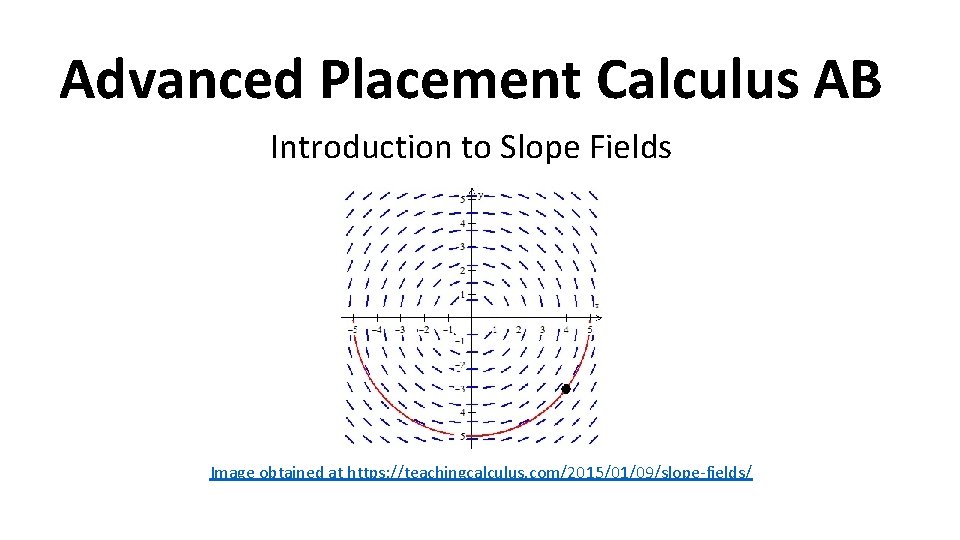
Advanced Placement Calculus AB Introduction to Slope Fields Image obtained at https: //teachingcalculus. com/2015/01/09/slope-fields/

What are Slope Fields? Slope fields are graphical representations of differential equations. Recall that a differential equation is an equation that involves a derivative. The slope field, as its name might indicate, is a visualization of the slope of a solution curve to the differential equation throughout the coordinate plane. Remembering our work with antiderivatives, we began by writing a general solution, which gave the family of functions that had the indicated derivative. Think of a slope field as a graphical representation of that family of functions. If a solution point was given, we were able to find the particular solution to the differential equation. The particular solution could be shown on the slope field by sketching a curve passing through that point that follows the direction of the slope field. On the AP Calculus AB exam, you may be asked to sketch a slope field for a differential equation expressed in terms of x and y. You would be instructed to sketch a particular solution at an indicated point, as well.

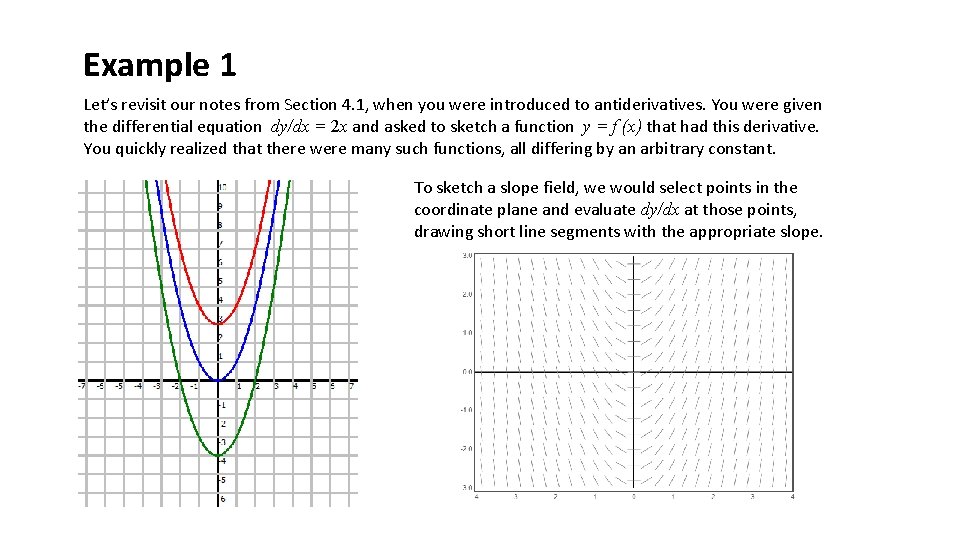
Example 1 Let’s revisit our notes from Section 4. 1, when you were introduced to antiderivatives. You were given the differential equation dy/dx = 2 x and asked to sketch a function y = f (x) that had this derivative. You quickly realized that there were many such functions, all differing by an arbitrary constant. To sketch a slope field, we would select points in the coordinate plane and evaluate dy/dx at those points, drawing short line segments with the appropriate slope.

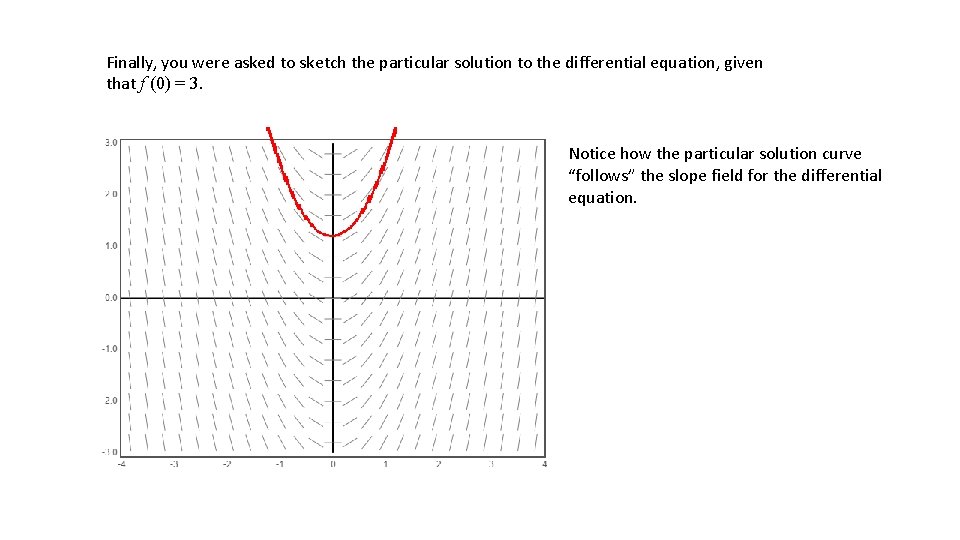
Finally, you were asked to sketch the particular solution to the differential equation, given that f (0) = 3. Notice how the particular solution curve “follows” the slope field for the differential equation.

Slope Fields on the Advanced Placement Calculus AB Exam The differential equations you may encounter on the AP Exam will not be as simple as the one we began Section 4. 1 with. The differential equations will likely be of the form dy/dx = f (x, y). But sketching a slope field for differential equations of this form is not overly difficult, as the next example will illustrate. Example 2 Sketch a slope field for the differential equation at the dy/dy = xy at the 15 points indicated on the graph. Solution You can begin by selecting one of the labeled points. Substitute the coordinates into dy/dx and compute the slope. Once the slope is computed, sketch a short line segment with the computed slope. Selecting (1, 1), we have dy/dx = 1(1) = 1. Sketch a line segment with slope of 1 at (1, 1).

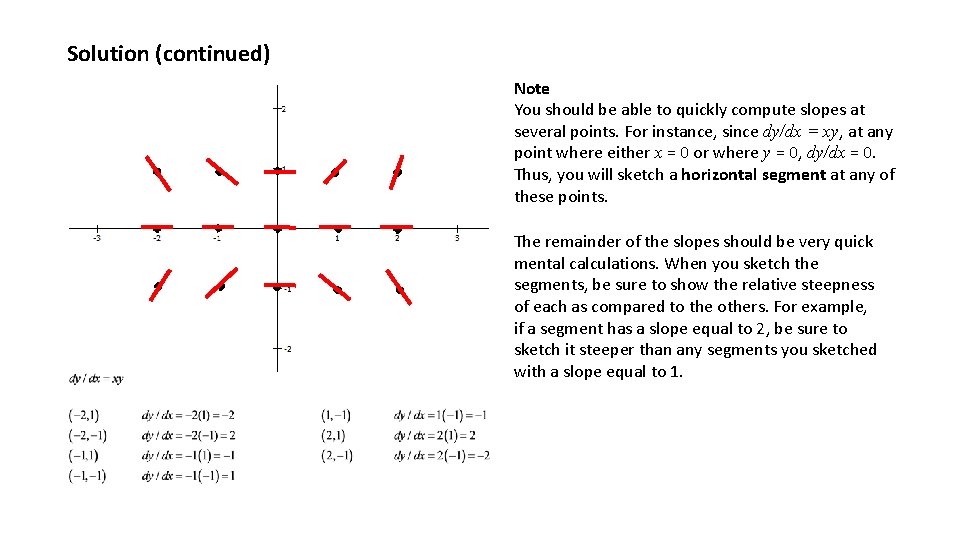
Solution (continued) Note You should be able to quickly compute slopes at several points. For instance, since dy/dx = xy, at any point where either x = 0 or where y = 0, dy/dx = 0. Thus, you will sketch a horizontal segment at any of these points. The remainder of the slopes should be very quick mental calculations. When you sketch the segments, be sure to show the relative steepness of each as compared to the others. For example, if a segment has a slope equal to 2, be sure to sketch it steeper than any segments you sketched with a slope equal to 1.

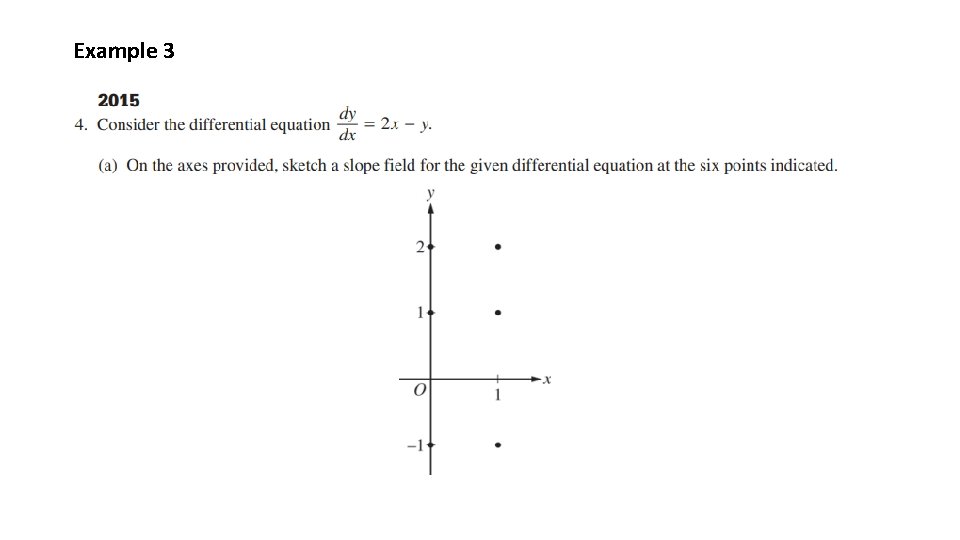
Example 3

Solution

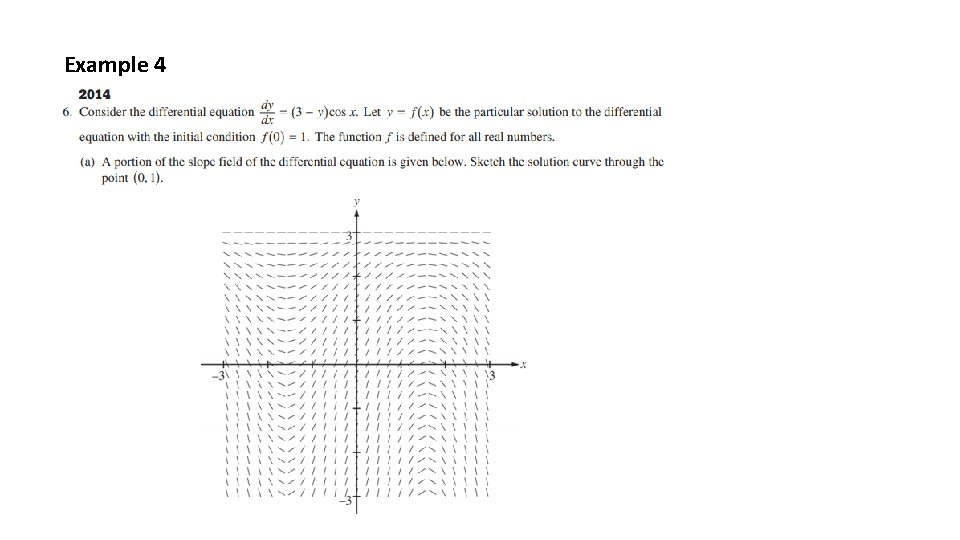
Example 4

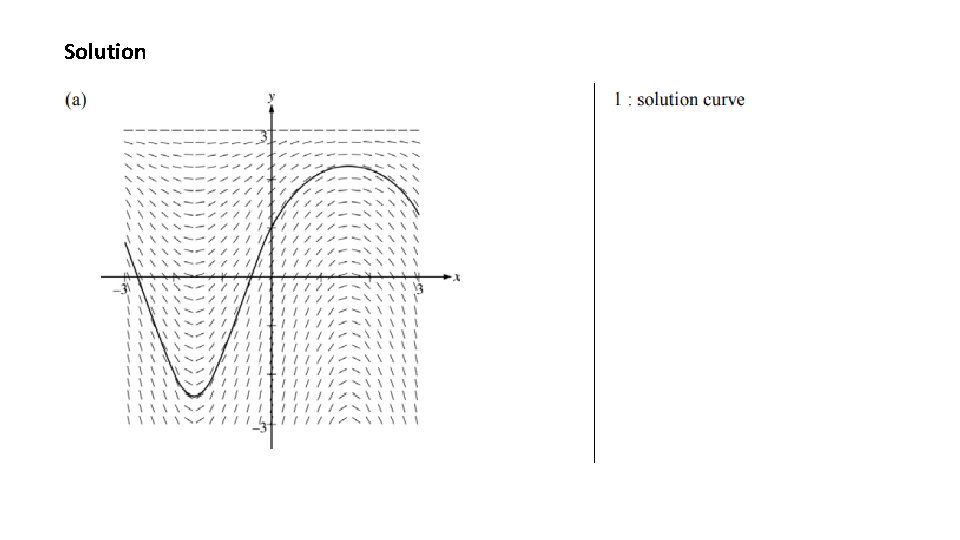
Solution

Example 5

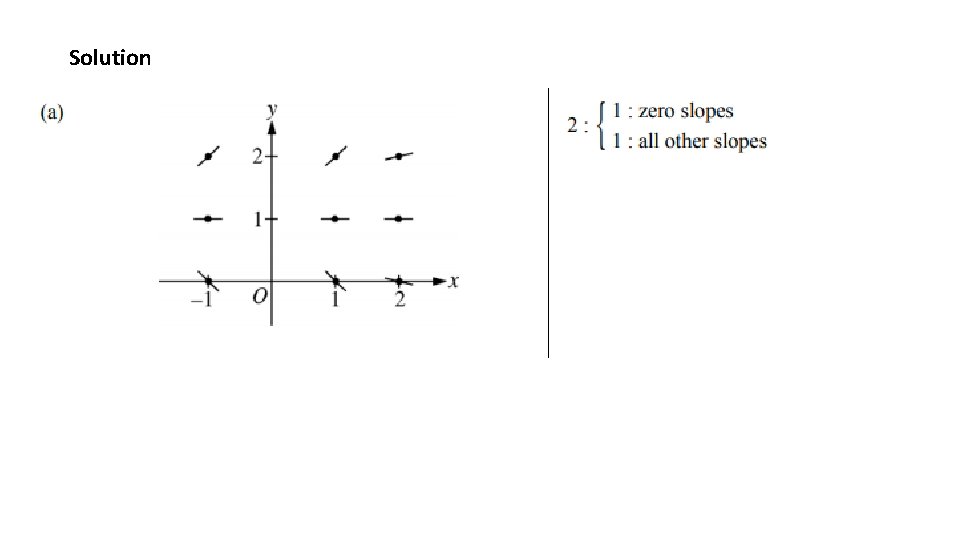
Solution