Advanced Physics Chapter 5 Circular Motion Gravitation Chapter

Advanced Physics Chapter 5 Circular Motion: Gravitation

Chapter 5: Circular Motion: Gravitation z 5 -1 Kinematics of Uniform Circular Motion z 5 -2 Dynamics of Uniform Circular Motion z 5 -3 Highway Curves, Banked and Unbanked z 5 -4 Nonuniform Circular Motion z 5 -6 Newton’s Law of Universal Gravitation z 5 -7 Gravity near the Earth's Surface z 5 -8 Satellites and “Weightlessness” z 5 -10 Types of Forces in Nature

5 -1 Kinematics of Uniform Circular Motion z object that moves in a circle with constant speed z magnitude of velocity is constant but direction is changing

5 -1 Kinematics of Uniform Circular Motion Centripetal (radial) acceleration (ar or ac) z center-seeking acceleration z acceleration directed toward the center of the circle z velocity and acceleration vectors are perpendicular to each other

5 -1 Kinematics of Uniform Circular Motion Velocity z v = d/t z d = 2 r z so v = 2 r/T z where T = period of revolution (sec) z and f = frequency (sec-1) z T = 1/f

5 -1 Kinematics of Uniform Circular Motion Centripetal acceleration za. R = v 2/r za. R = 4 2 r/T 2

5 -2 Dynamics of Uniform Circular Motion According to Newton’s Second Law: Fnet = ma z FR = ma. R = mv 2/r z net centripetal force ( FR) must be directed toward center (why? ) z centripetal force vs. centrifugal force

5 -3 Highway Curves, Banked and Unbanked z When a car goes around a curve in the road what keeps it on the road? z When is the friction between the tires and the road greater, when they are rolling or sliding? z So to keep a car on the road on a curve we must……

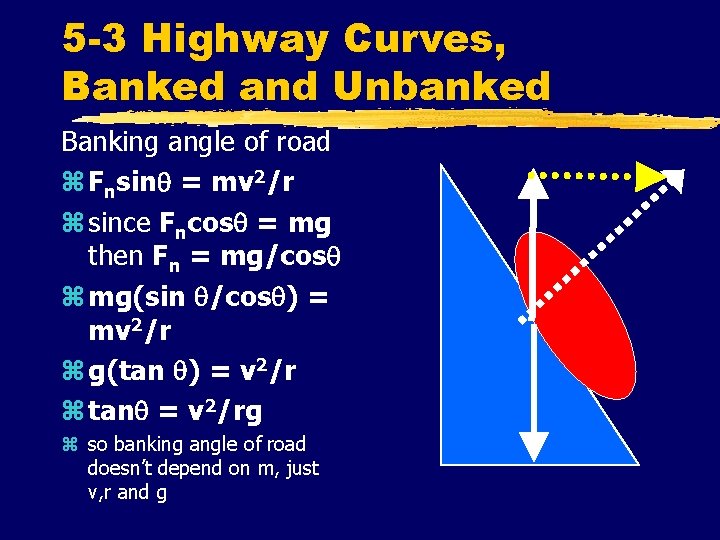
5 -3 Highway Curves, Banked and Unbanked z Banking a curve reduces skidding why? z Fn is at an angle toward the center of the curve z so a portion of the Fn goes into FR so the tires need to supply less frictional force to make up for the remaining FR needed

5 -3 Highway Curves, Banked and Unbanked Banking angle of road z Fnsin = mv 2/r z since Fncos = mg then Fn = mg/cos z mg(sin /cos ) = mv 2/r z g(tan ) = v 2/r z tan = v 2/rg z so banking angle of road doesn’t depend on m, just v, r and g

5 -4 Nonuniform Circular Motion z. For an object in UCM; the only acceleration is due to radial (centripetal) acceleration za. R is caused by what? Equation? z. But if the object in circular motion is speeding up or slowing down there is another type of acceleration, tangential acceleration

5 -4 Nonuniform Circular Motion Tangential acceleration (atan) z. Acceleration caused by the change in the magnitude of the velocity of an object moving in a circular path zatan = v/ t

5 -4 Nonuniform Circular Motion Total vector acceleration (a) z. Acceleration caused by the change in the magnitude and direction of the velocity of an object moving in a circular path z. It is the sum of both the tangential and radial acceleration of an object za = atan + a. R

5 -4 Nonuniform Circular Motion Total vector acceleration (a) za = atan + a. R The magnitude of a at any moment is: za = 2 (a tan + 2 a R 1/2 )

5 -6 Newton’s Law of Universal Gravitation z every particle in the Universe attracts every other particle with a force that is proportional to their masses and inversely proportional to the distance between them

5 -6 Newton’s Law of Universal Gravitation z the force of gravity acts along a line joining the two particles. z. F = Gm 1 m 2/d 2 z G = 6. 67 x 10 – 11 Nm 2/kg 2

5 -6 Newton’s Law of Universal Gravitation z Find the force of gravity between two electrons that are 2. 3 x 10 -2 nm apart z Answer: y 1. 05 x 10 -49 N

5 -7 Gravity near the Earth's Surface z Since the force of gravity is equal to the weight of an object… z Gmome/r 2 = mog z so…. z g = Gme/r 2 z so. . gravity (g) doesn’t depend on the mass of the object, just G, me and r!

5 -8 Satellites and “Weightlessness” z Why do satellites orbit the Earth? z How can a person orbiting the Earth experience “weightlessness”? z Many nasty effects of weightlessness on the body

5 -8 Satellites and “Weightlessness” z What is the relationship between Fn, Fa, and Fg in the following situations? z stationary z accelerating up z accelerating down z in free-fall

5 -10 Types of Forces in Nature Four different fundamental forces: z gravitational force y force between any two objects z electromagnet force y force between any two charged objects z strong nuclear force y force that holds the nucleus together z weak nuclear force y force involved in certain types of nuclear decay

5 -10 Types of Forces in Nature What is GUT?