Advanced Molecular Dynamics Velocity scaling Andersen Thermostat Hamiltonian

Advanced Molecular Dynamics Velocity scaling Andersen Thermostat Hamiltonian & Lagrangian Appendix A Nose-Hoover thermostat

Naïve approach Velocity scaling Do we sample the canonical ensemble?

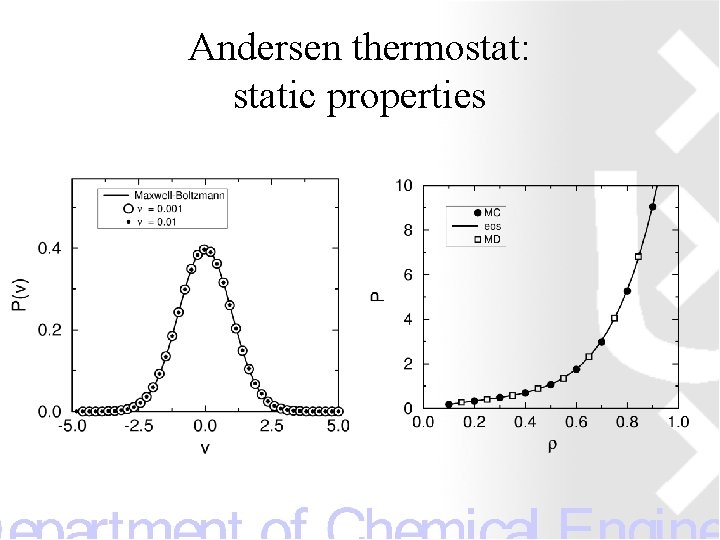
Partition function Maxwell-Boltzmann velocity distribution

Fluctuations in the momentum: Fluctuations in the temperature

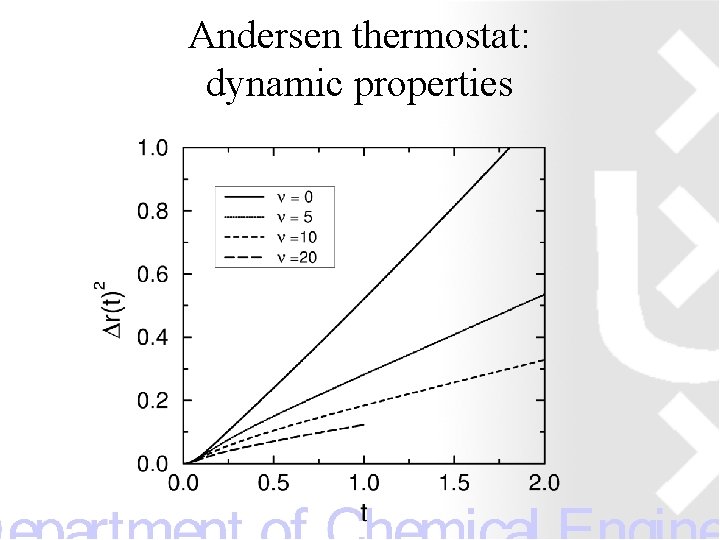
Andersen thermostat Every particle has a fixed probability to collide with the Andersen demon After collision the particle is give a new velocity The probabilities to collide are uncorrelated (Poisson distribution)

Velocity Verlet:

Andersen thermostat: static properties

Andersen thermostat: dynamic properties

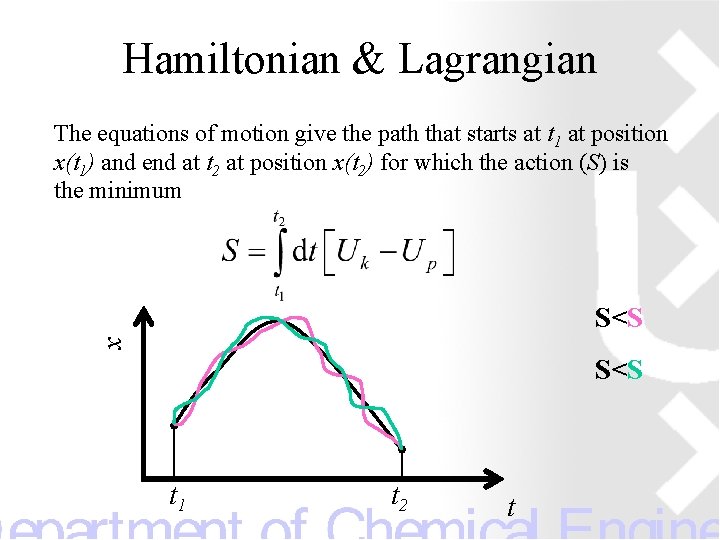
Hamiltonian & Lagrangian The equations of motion give the path that starts at t 1 at position x(t 1) and end at t 2 at position x(t 2) for which the action (S) is the minimum x S<S t 1 t 2 t

Example: free particle Consider a particle in vacuum: v(t)=vav η(t)=0 for all t Always > 0!!

η(t) is small At the boundaries: Calculusη(t of)=0 variation and η(t )=0 1 2 True path for which S is minimum η(t) should be such the δS is minimal

This term should be zero for all η(t) so […] η(t) Integration by parts If this term 0, S has a minimum Zero because of the boundaries η(t 1)=0 and η(t 2)=0 Newton A description which is independent of the coordinates

Lagrangian Cartesian coordinates (Newton) → Generalized coordinates (? ) Lagrangian Action The true path plus deviation

Partial integration Desired format […] η(t) Should be 0 for all paths Equations of motion Conjugate momentum Lagrangian equations of motion

Newton? Valid in any coordinate system: Cartesian Conjugate momentum

Pendulum Equations of motion in terms of l and θ Conjugate momentum

Lagrangian dynamics We have: 2 nd order differential equation Two 1 st order differential equations With these variables we can do statistical thermodynamics Change dependence:

Legrendre transformation Example: thermodynamics We have a function that depends on and we would like We prefer to control T: S→T Legendre transformation Helmholtz free energy

Hamiltonian Hamilton’s equations of motion

Newton? Conjugate momentum Hamiltonian

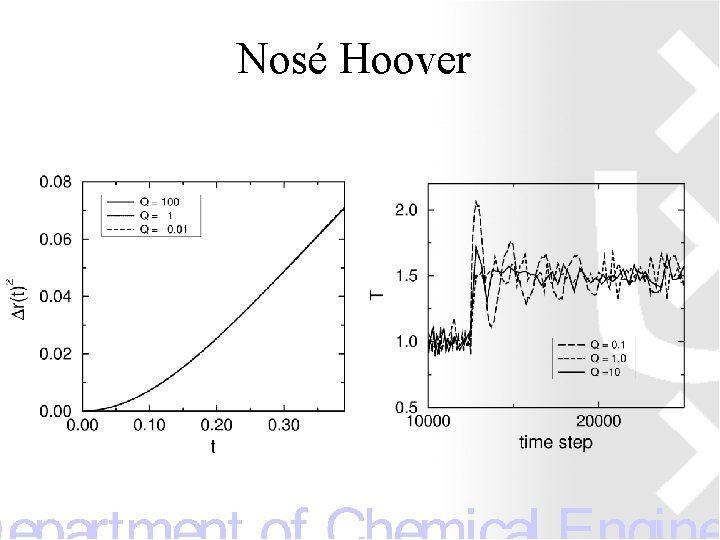
Nosé thermostat Lagrangian Hamiltonian Extended system 3 N+1 variables Associated mass Conjugate momentum

Nosé and thermodynamics Delta functions Recall MD MC Gaussian integral Constant plays no role in thermodynamics

Lagrangian Hamiltonian Conjugate momenta Equations of motion: Equations of Motion

Nosé Hoover