Advanced LP models column generation min max min

Advanced LP models column generation

min max

min max OK OK ?

Bin packing example bins of size K items of different types items of type i have size s(i) and there are n(i) of them problem put all items into the bins minimizing the number of bins

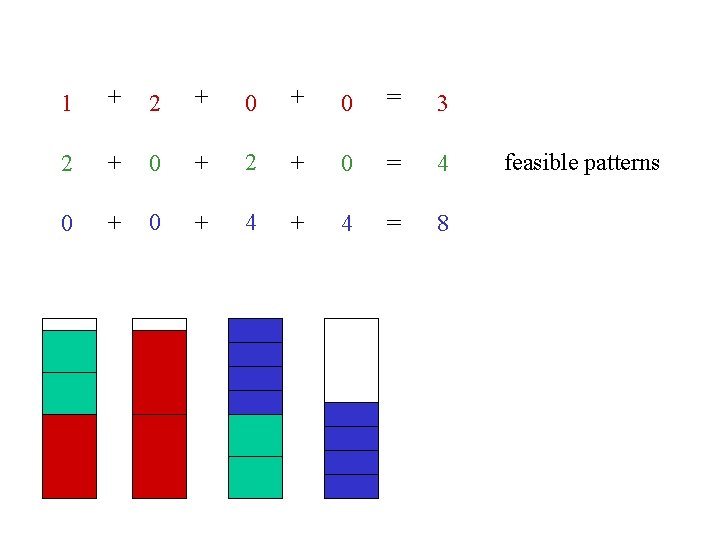
1 + 2 + 0 = 3 2 + 0 + 2 + 0 = 4 0 + 4 + 4 = 8 feasible patterns

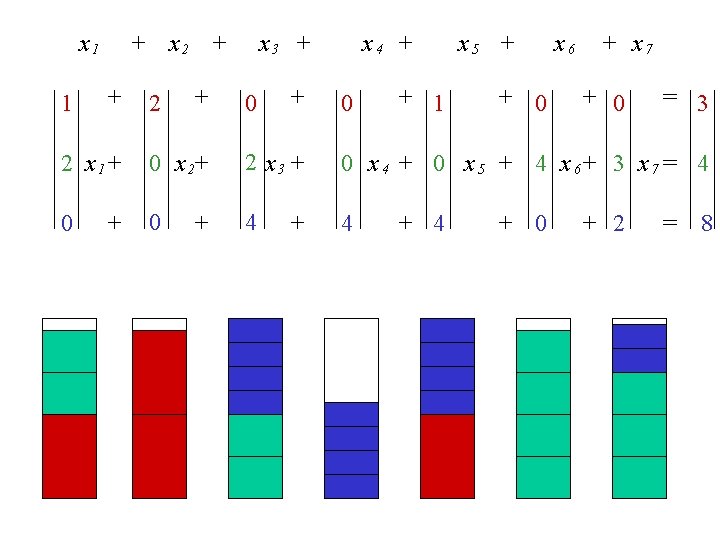
x 1 1 + x 2 + + 2 x 11 + 0 + 2 + x 3 + 0 + x 4 + 0 + 1 x 5 + + 0 x 6 + x 7 + 0 = 3 0 x 12+ 2 x 13 + 0 1 x 4 + 0 0 x 5 + 4 0 x 6 + 3 0 x 7 = 4 0 4 4 + + + 4 + 0 + 2 = 8

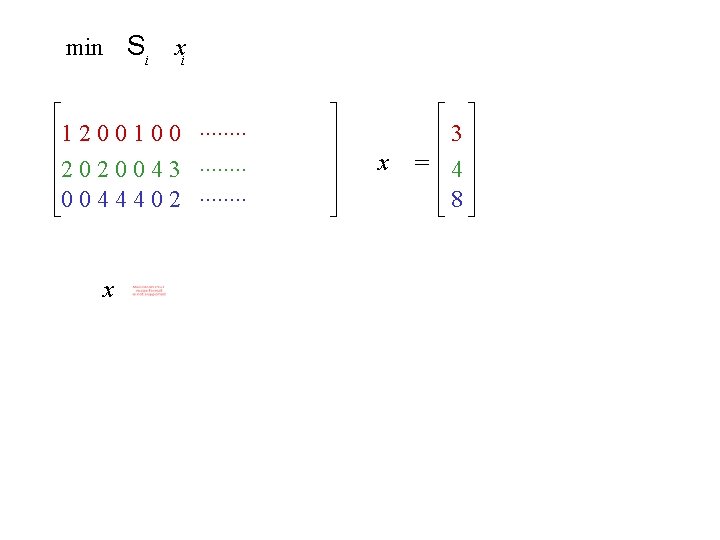
min Si xi 1 2 0 0 1 0 0. . . . 2 0 0 4 3. . . . 0 0 4 4 4 0 2. . . . x integer 3 x = 4 8

min max OK OK ?

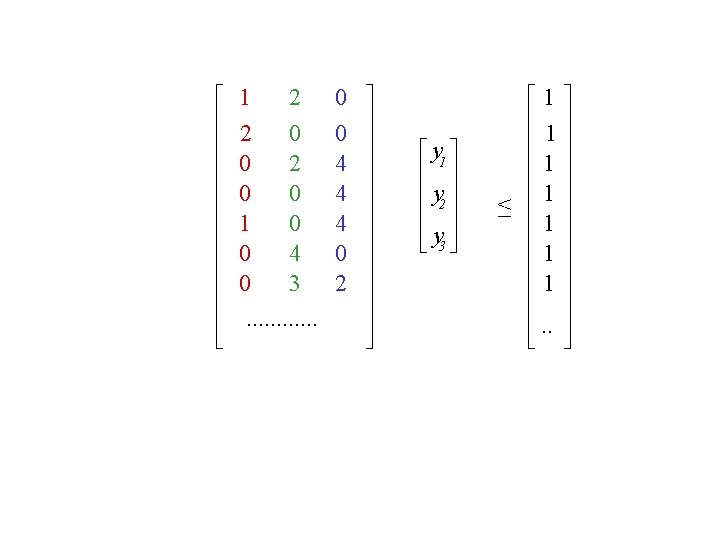
1 2 0 0 1 20 0. . . . 0 0 2 0 0 04 3 2. . . . 4 0 0 4 4 4 00 2 0. . . . 4 1 0 4 0 0 3 2. . . y 1 y 2 y 3 < 1 1 1 1. .

1 y 1 + 2 y 2 + 0 y 3 < 1 2 y 1 + 0 y 2 + 0 y 3 < 1 a 1 y 1 + a 2 y 2 + a 3 y 3 < 1 for all feasible patterns a 1 a 2 a 1 s 1 + a 2 s 2 + a 3 s 3 < max a 1 y 1 + a 2 y 2 + a 3 y 3 a 3 K < 1

max a 1 y 1 + a 2 y 2 + a 3 y 3 a 1 s 1 + a 2 s 2 + a 3 s 3 < a 1 a 2 a 3 K integer knapsack ! if max < 1 optimality ! otherwise add pattern maximizing knapsack

example bin capacity = 20 3 types: type 1: size = 7; quantity = 50 type 2: size = 5; quantity =100 type 3: size = 3; quantity = 70 x starting patterns generated patterns 2 0 2 25 0 4 0 y= ( 024 1/4 0 1/4 y= ( 1/3 4. 25 y= (. 35 0 0 6 0 1 5 53 bins 1/2 ) 1/6 ). 15 )

however, change quantities to solution is : x 1 x 2 x 3 x 4 52 = 26 = 23. 3 = 0 = 3. 8 53. 1 how to get an integer solution? 97 71

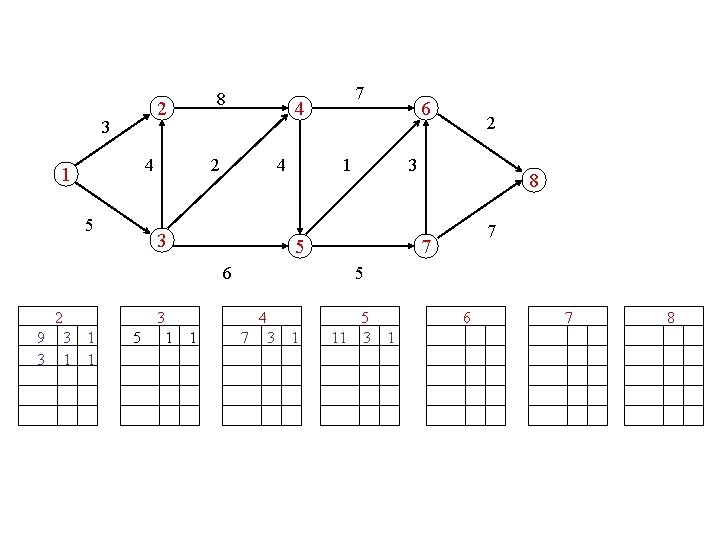
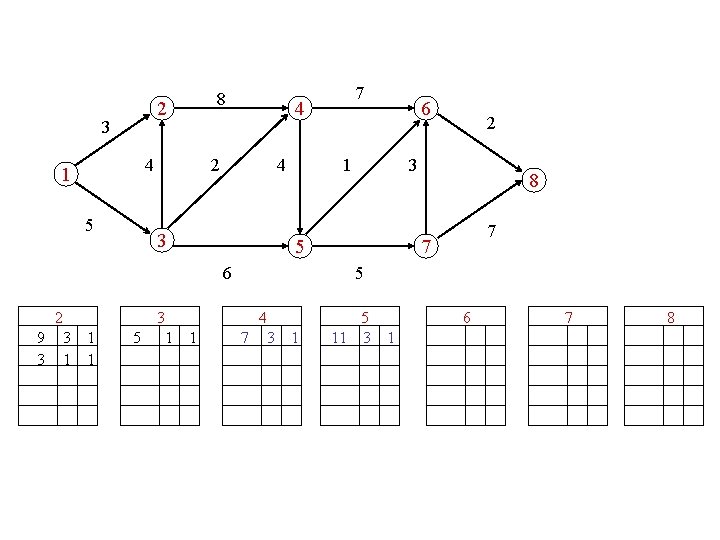
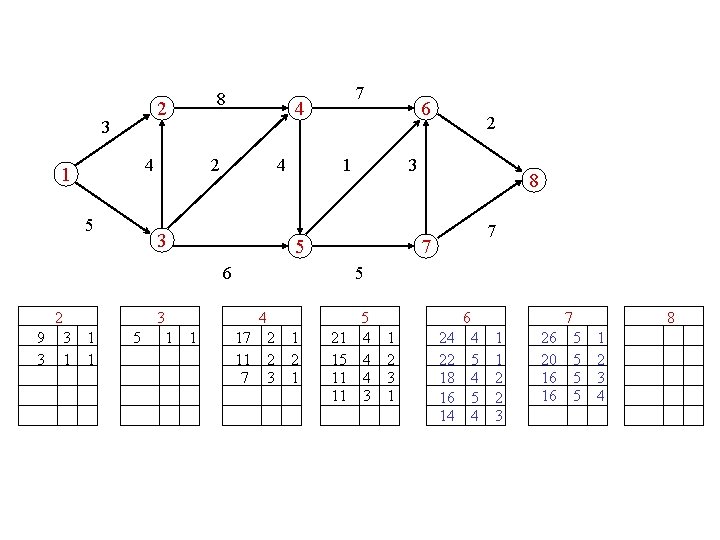
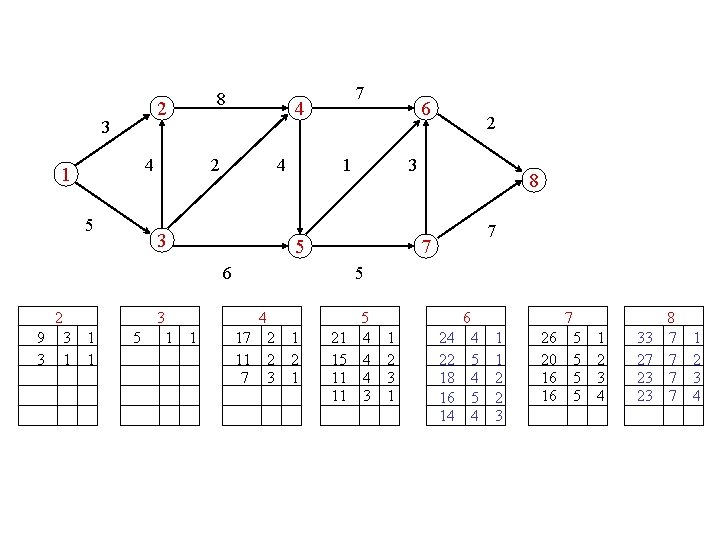
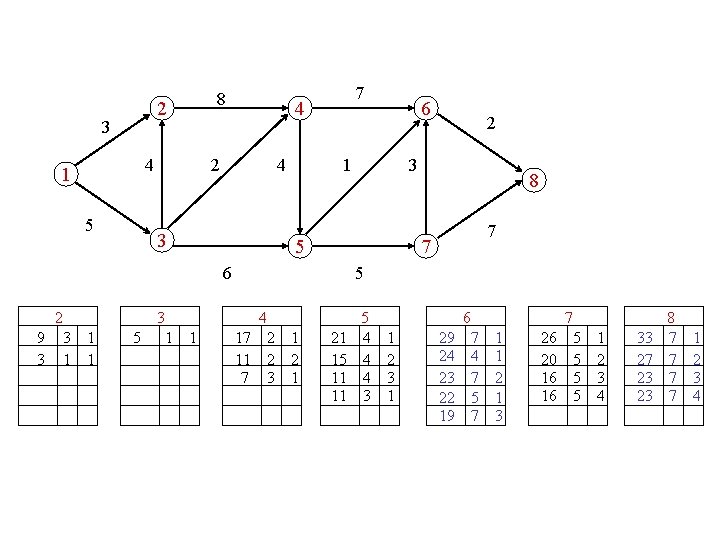
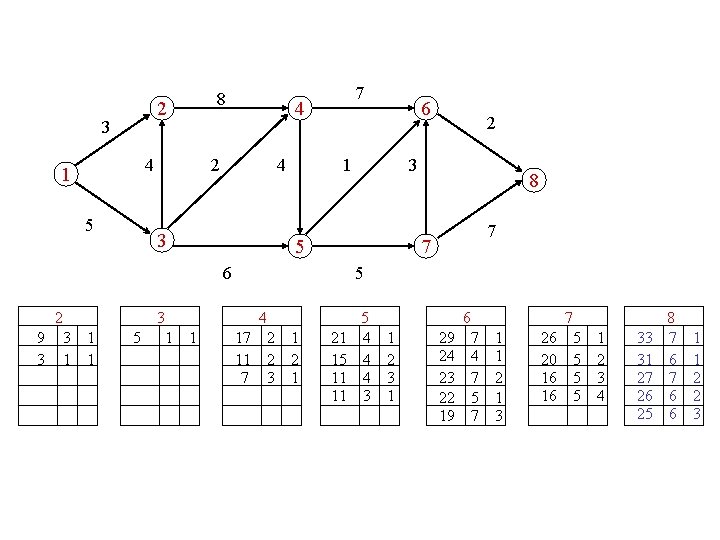
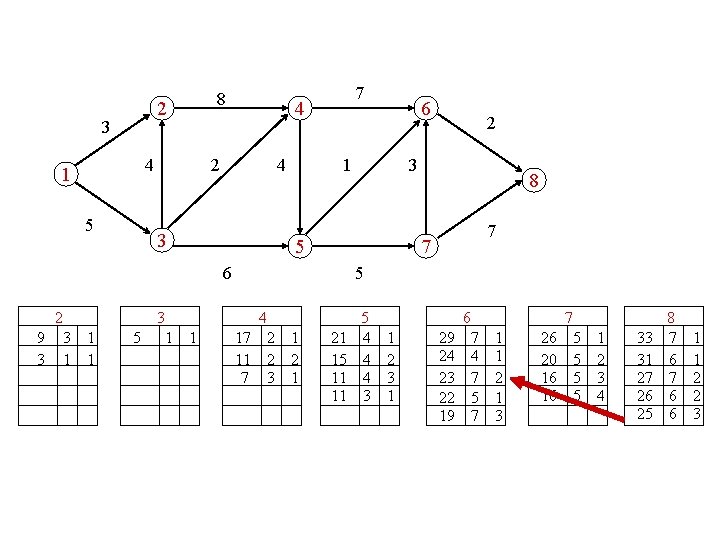
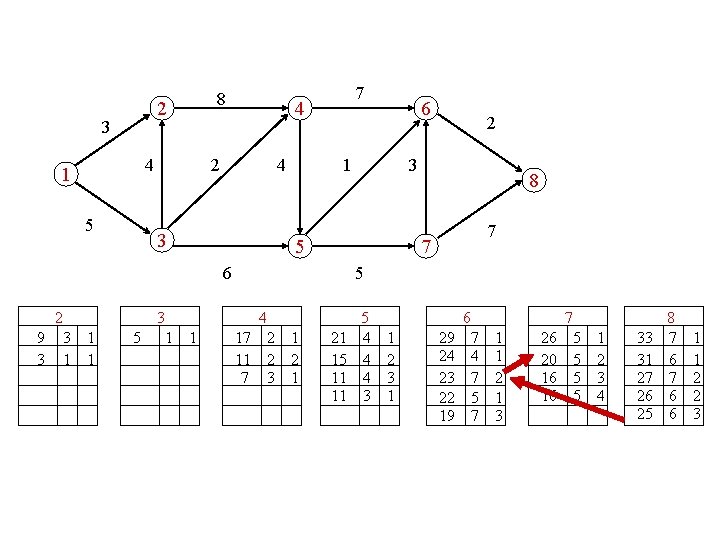
? ? compute the first |J|+1 knapsack solutions

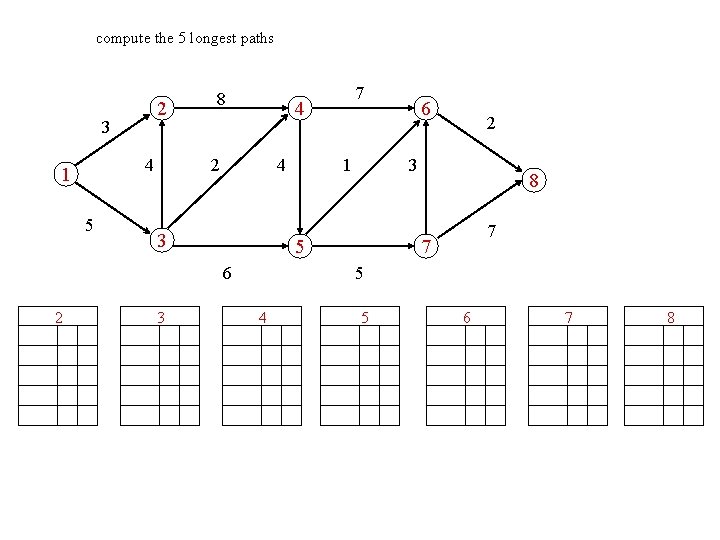
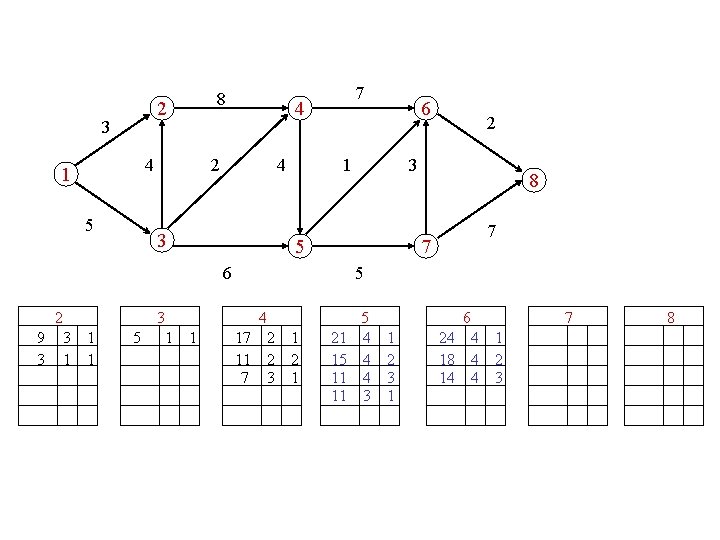
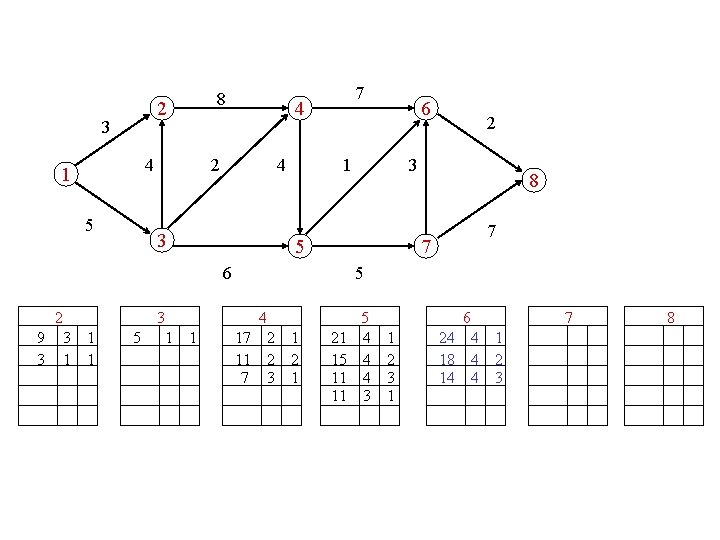
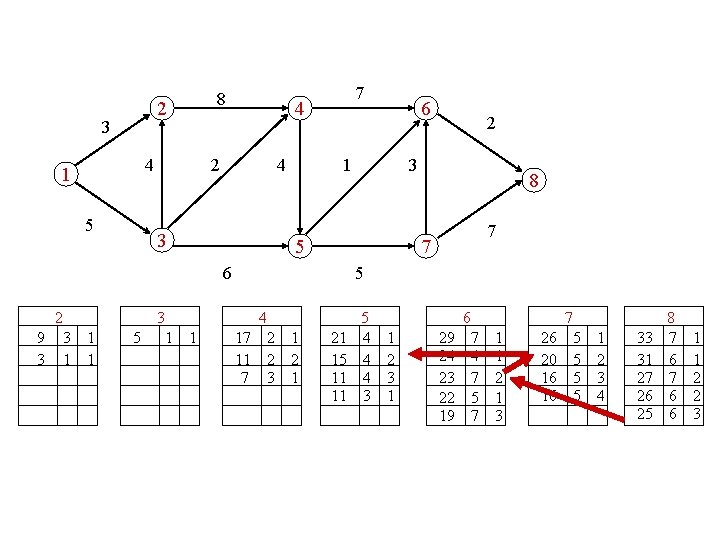
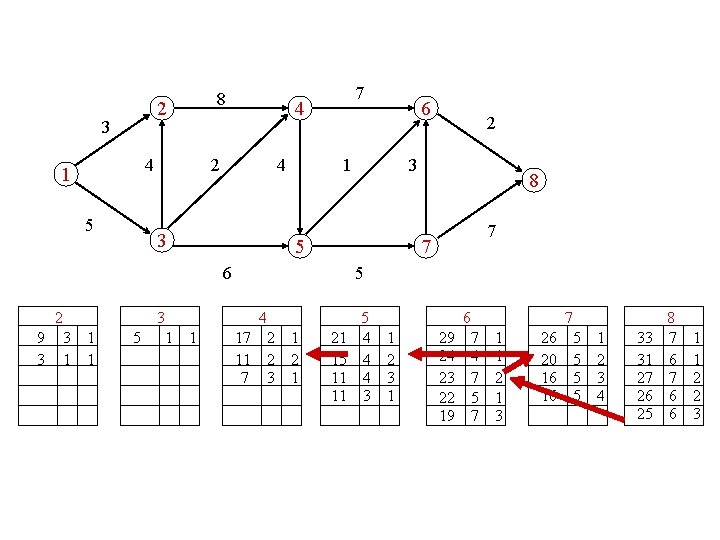
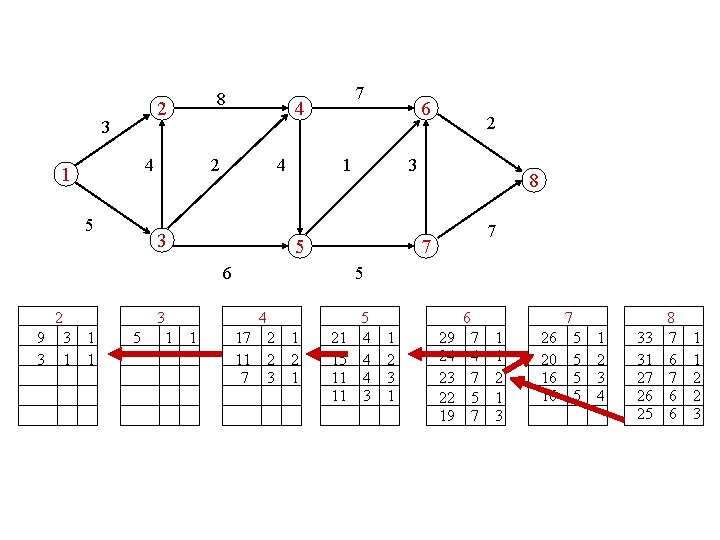
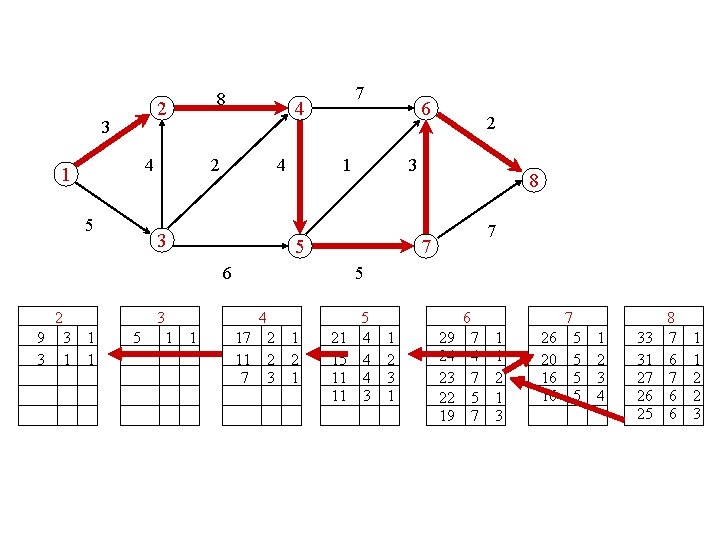
compute the 5 longest paths 2 3 4 1 5 8 4 2 4 3 3 1 6 2 3 5 6 2 7 8 7 7 5 4 5 6 7 8

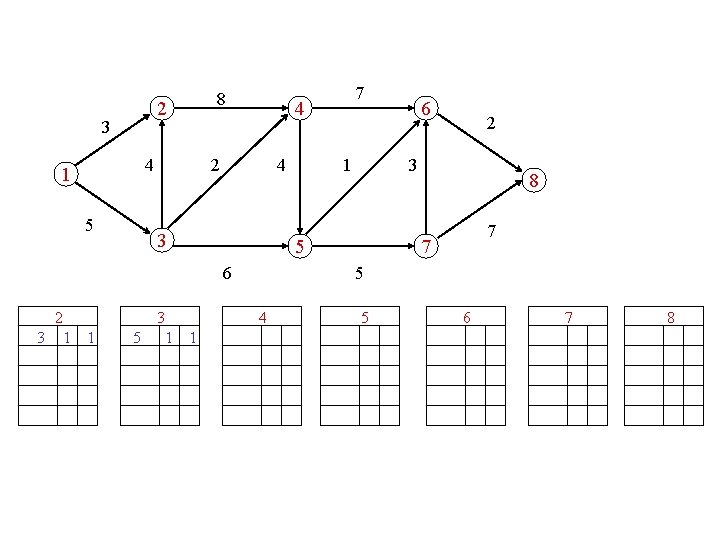
8 2 3 4 1 5 4 2 4 3 5 3 1 1 2 8 7 7 5 4 1 6 3 5 6 2 3 1 1 7 5 6 7 8

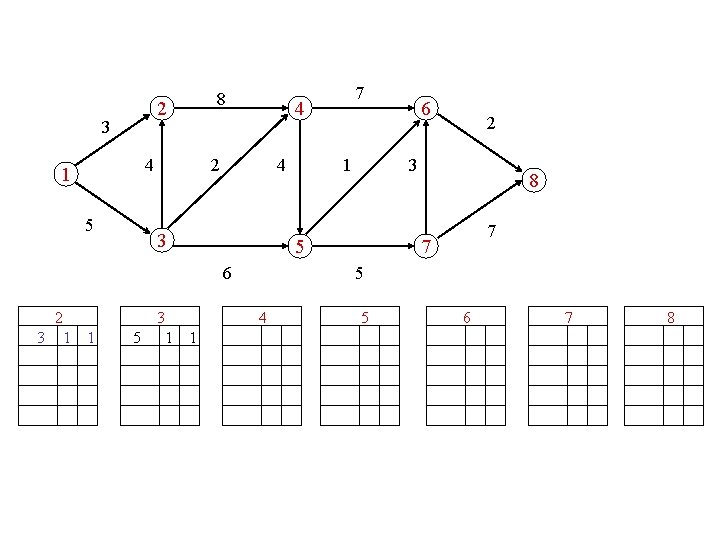
8 2 3 4 1 5 4 2 4 3 5 3 1 1 2 8 7 7 5 4 1 6 3 5 6 2 3 1 1 7 5 6 7 8

8 2 3 4 1 5 4 2 4 3 5 3 1 6 1 1 2 3 5 6 2 9 3 1 1 7 8 7 7 5 4 7 3 1 5 11 3 6 1 7 8

8 2 3 4 1 5 4 2 4 3 5 3 1 6 1 1 2 3 5 6 2 9 3 1 1 7 8 7 7 5 4 7 3 1 5 11 3 6 1 7 8

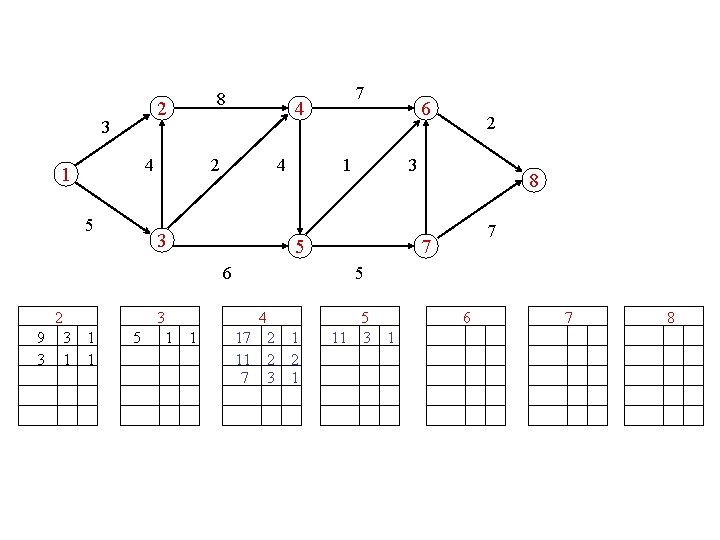
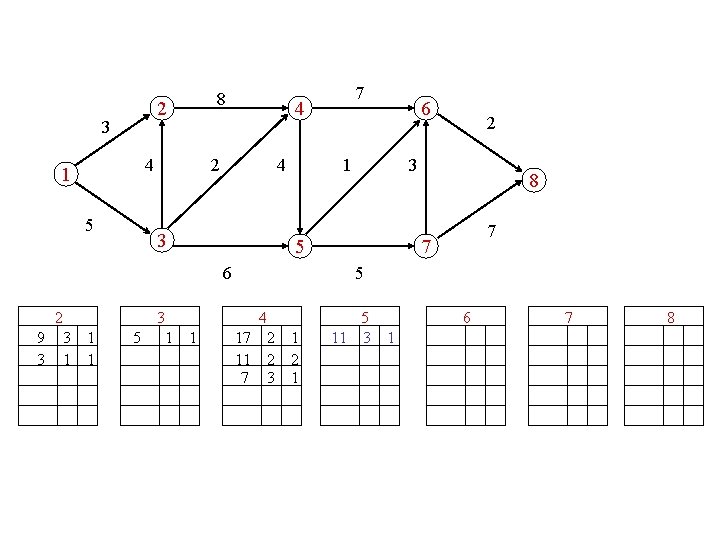
8 2 3 4 1 5 4 2 4 3 5 3 1 6 1 1 2 3 5 6 2 9 3 1 1 7 8 7 7 5 4 17 2 11 2 7 3 1 2 1 5 11 3 6 1 7 8

8 2 3 4 1 5 4 2 4 3 5 3 1 6 1 1 2 3 5 6 2 9 3 1 1 7 8 7 7 5 4 17 2 11 2 7 3 1 2 1 5 11 3 6 1 7 8

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 2 3 1 6 24 4 18 4 14 4 7 1 2 3 8

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 2 3 1 6 24 4 18 4 14 4 7 1 2 3 8

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 24 22 18 16 14 6 4 5 4 1 1 2 2 3 26 20 16 16 7 5 5 8 1 2 3 4

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 24 22 18 16 14 6 4 5 4 1 1 2 2 3 26 20 16 16 7 5 5 1 2 3 4 33 27 23 23 8 7 7 1 2 3 4

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 27 23 23 8 7 7 1 2 3 4

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 31 27 26 25 8 7 6 6 1 1 2 2 3

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 31 27 26 25 8 7 6 6 1 1 2 2 3

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 31 27 26 25 8 7 6 6 1 1 2 2 3

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 31 27 26 25 8 7 6 6 1 1 2 2 3

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 31 27 26 25 8 7 6 6 1 1 2 2 3

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 31 27 26 25 8 7 6 6 1 1 2 2 3

8 2 3 4 1 5 7 4 2 4 3 1 5 3 1 1 2 3 5 8 7 7 6 2 9 3 1 1 6 5 4 17 2 11 2 7 3 1 21 15 11 11 5 4 4 4 3 1 29 24 23 22 19 6 7 4 7 5 7 1 1 2 1 3 26 20 16 16 7 5 5 1 2 3 4 33 31 27 26 25 8 7 6 6 1 1 2 2 3

< max a 1 y 1 + a 2 y 2 + a 3 y 3 a 1 s 1 + a 2 s 2 + a 3 s 3 < a 1 a 2 a 3 1 K integer V(j)=optimal value for a knapsack of capacity j V(j) = max { V(j - s(i)) + y(i) : i= 1, . . . , n} V(j) > V(j - s(i)) + y(i) V(K) < 1 V(j) > 0 i= 1, . . . , n; j=1, . . . , K

min max

max b(i) y(i) V(j) > V(j - s(i)) + y(i) i= 1, . . . , n; j=1, . . . , K V(K) < 1 V(j) > 0 however this is the dual problem we need the patterns which are in the primal so let’s make the dual of the above problem

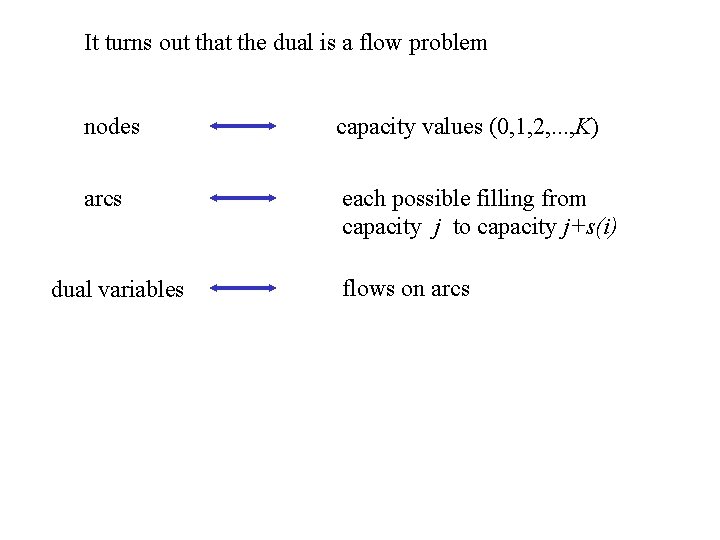
It turns out that the dual is a flow problem nodes capacity values (0, 1, 2, . . . , K) arcs each possible filling from capacity j to capacity j+s(i) dual variables flows on arcs

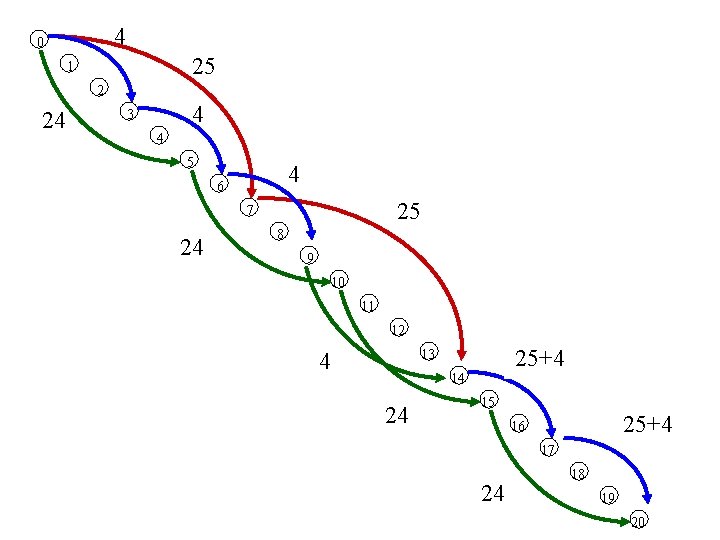
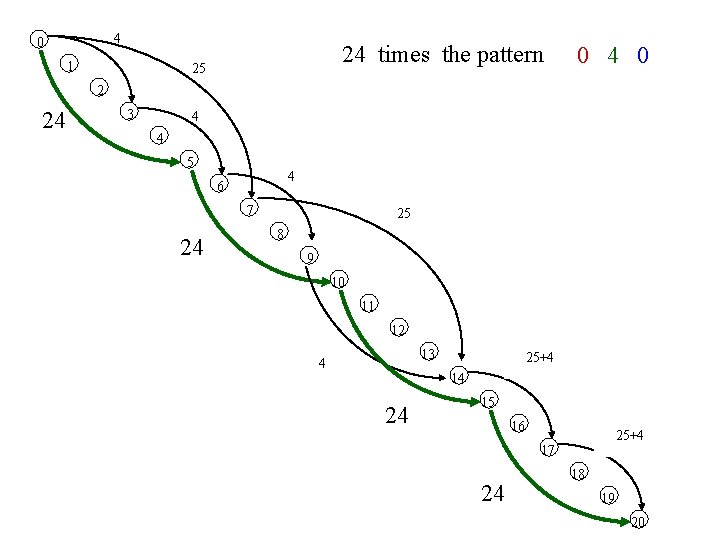
4 0 25 1 2 24 4 3 4 5 4 6 25 7 24 8 9 10 11 12 25+4 29 13 4 14 24 15 25+4 29 16 17 24 18 19 20

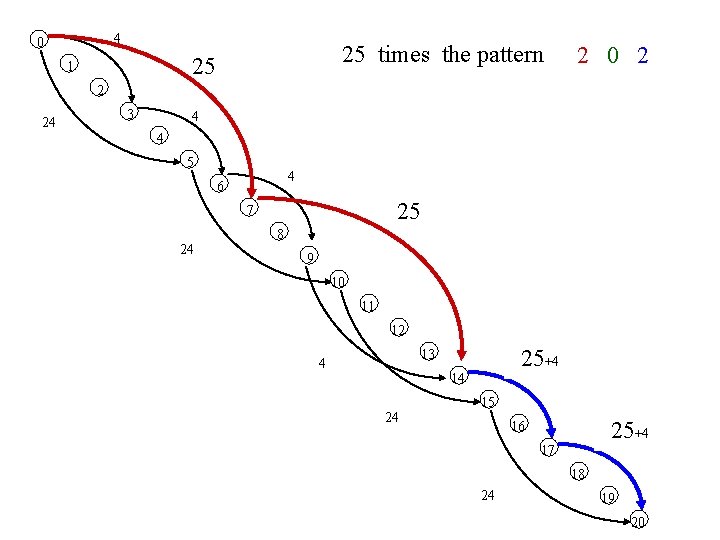
4 0 25 times the pattern 25 1 2 0 2 2 24 3 4 4 5 4 6 25 7 24 8 9 10 11 12 25+4 29 13 4 14 24 15 25+4 16 17 18 24 19 20

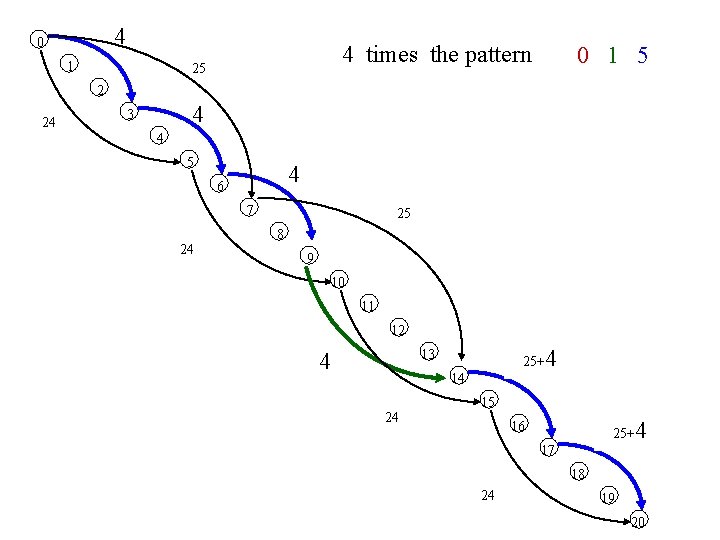
4 0 1 24 times the pattern 25 0 4 0 2 24 3 4 4 5 4 6 7 24 25 8 9 10 11 12 25+4 29 13 4 14 24 15 16 25+4 17 24 18 19 20

4 0 1 4 times the pattern 25 0 1 5 2 24 4 3 4 5 4 6 7 24 25 8 9 10 11 12 25+4 29 13 4 14 24 15 16 25+ 17 4 18 24 19 20

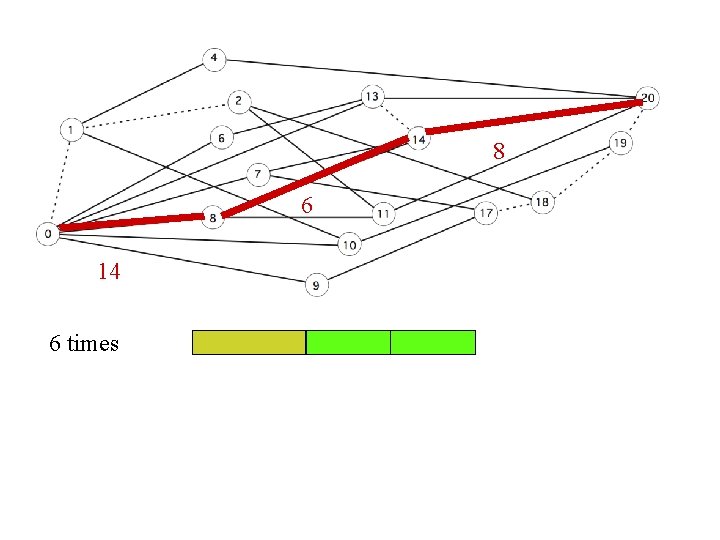
8 6 14 6 times

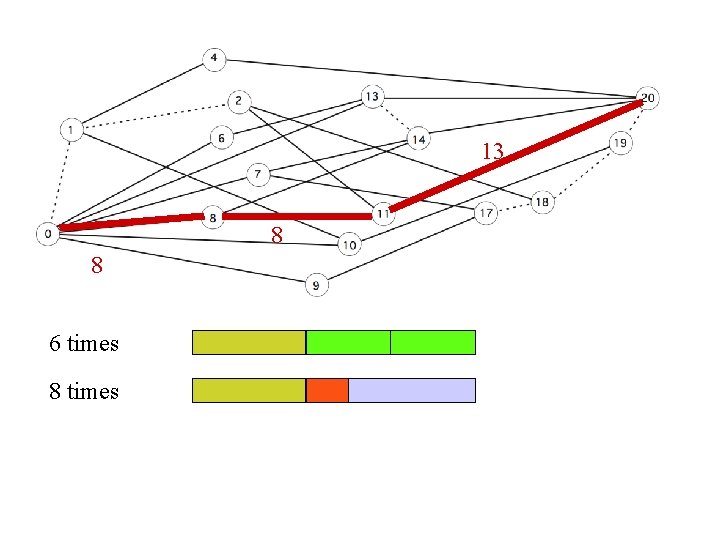
13 8 8 6 times 8 times

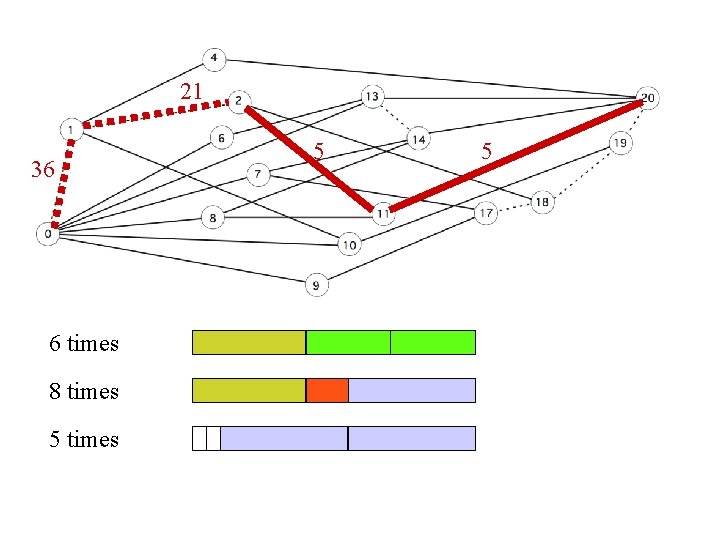
21 36 6 times 8 times 5 5