Advanced Higher Topic Past Papers Algebra Unit 1

Advanced Higher Topic Past Papers –Algebra Unit 1 Outcome 1 2001 A 5. (a) Obtain partial fractions for (2) A 6. Expand (5) and simplify as far as possible. 2002 A 8. Express in the form stating the values of the constants A, B and C. (3) 2004 2. Obtain the binomial expansion of (3) 5. (2) Express in partial fractions. 2005 13. Express in partial fractions. (4) 2007 1. Express the binomial expansion of for integers a, b, c, d and e. (4) 4. Express (3) in partial fractions. 2008 4. Express in partial fractions. (3) 8. Write down and simplify the general term in the expansion of Hence, or otherwise, obtain the term in x 14. (3) (2) 2009 5 8. (a) Write down the binomial expansion of (1 + x). 5 (b) Hence show that (0. 9) is 0. 59049. 14. Express in partial fractions. (1) (2) (4) 2011 Express in partial fractions Use the binomial theorem to expand Lanark Grammar Mathematics Department (2) and simplify your answer. (3) Mrs Leck

Advanced Higher Topic Past Papers –Algebra Unit 1 Outcome 1 2012 4. Write down and simplify the general term in the expansion of Hence, or otherwise, obtain the term independent of x. (a) Express 15. in partial fractions (3) (2) (b) Obtain the general solution of the differential equation (4) expressing your answer in the form 2013 1. Write down the binomial expansion of and simplify your answer. (4) 2014 2. Write down and simplify the general term in the expression (5) Hence, or otherwise, obtain the term in 14. (a) Given the series write down the sum to infinity when Hence obtain an infinite geometric series for For what values of r is this series valid? (b) Express in partial fractions. Hence, or otherwise, determine the first three terms of an infinite series for For what values of r does the series converge? Lanark Grammar Mathematics Department Mrs Leck

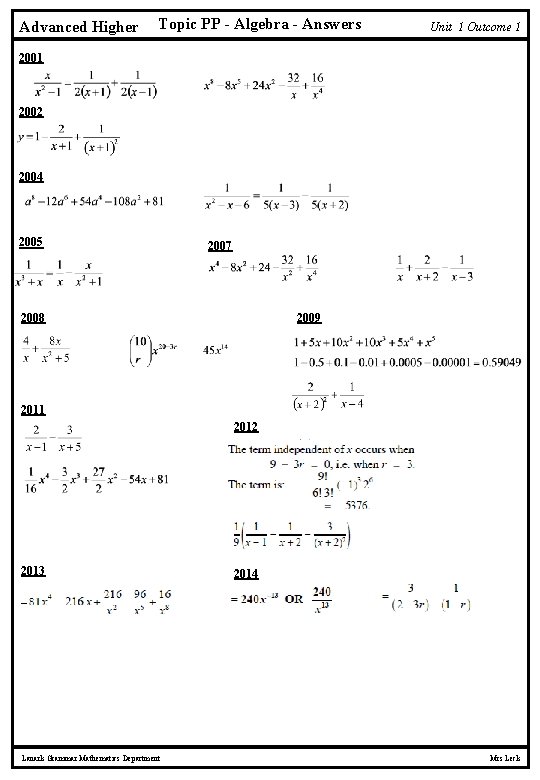
Advanced Higher Topic PP - Algebra - Answers Unit 1 Outcome 1 2002 2004 2005 2007 2008 2009 2011 2012 2013 Lanark Grammar Mathematics Department 2014 Mrs Leck