Advanced Geometry Inductive Reasoning Lesson 2 Angles Rays

Rays Drawn as: a line with one endpoint and one arrowhead N D Named

Angle Parts of an Angle vertex – the common endpoint B sides – the

Naming an Angle Use an angle symbol and… - the number inside the angle.

Examples: Name the sides of Write another name for Name all angles that have

Angle Classifications • Right angle – measures exactly 90° • Acute angle – measure

Examples: In the figure, bisects and are opposite rays, and

Angle Relationships Adjacent Angles Adjacent angles are beside each other. They share a vertex

Vertical Angles Vertical angles are NOT adjacent. They share a vertex only. Vertical angles

Linear Pair Angles of a linear pair ARE adjacent. They share a vertex and

Example: Name an angle pair that satisfies each condition. two angles that form a

Complementary Angles two angles sum of 90

Supplementary Angles two angles sum of 180 LINEAR PAIRS ARE ALWAYS SUPPLEMENTARY.

Example: If BCE and ECD are supplementary, find ECF and FCD.

Example: Find the measures of two supplementary angles if the difference in the measures

Slides: 18

Download presentation

Advanced Geometry Inductive Reasoning Lesson 2 Angles

Rays Drawn as: a line with one endpoint and one arrowhead N D Named by: 2 points and a ray symbol the endpoint must be named first the arrow always points to the right Opposite rays are two collinear rays that point in opposite directions.

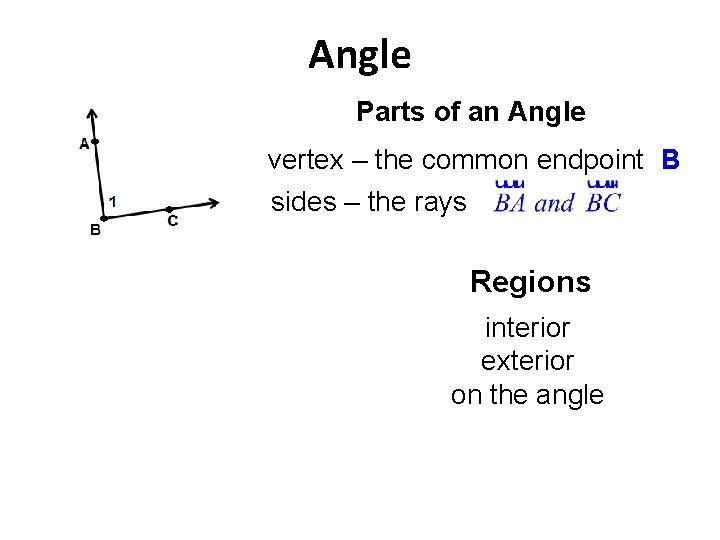
Angle Parts of an Angle vertex – the common endpoint B sides – the rays Regions interior exterior on the angle

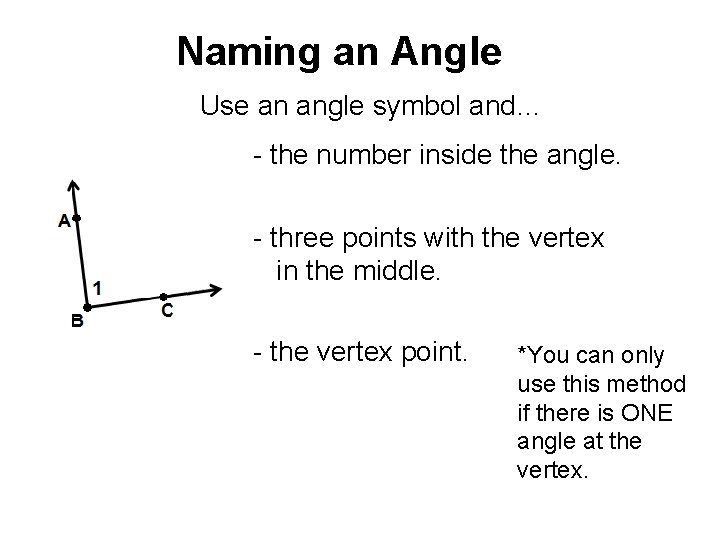
Naming an Angle Use an angle symbol and… - the number inside the angle. - three points with the vertex in the middle. - the vertex point. *You can only use this method if there is ONE angle at the vertex.

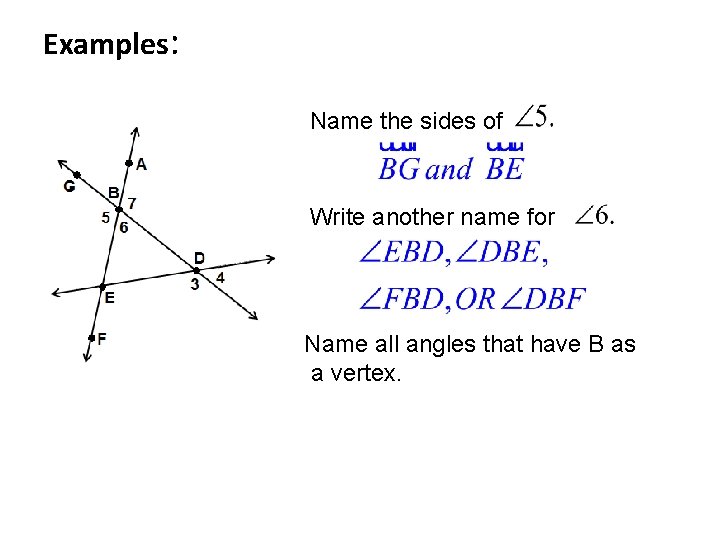
Examples: Name the sides of Write another name for Name all angles that have B as a vertex.

Angle Classifications • Right angle – measures exactly 90° • Acute angle – measure is less than 90° • Obtuse angle – measure is greater than 90° and less than 180° • Straight angle – an angle with a degree measure of exactly 180° (a. k. a. straight line)

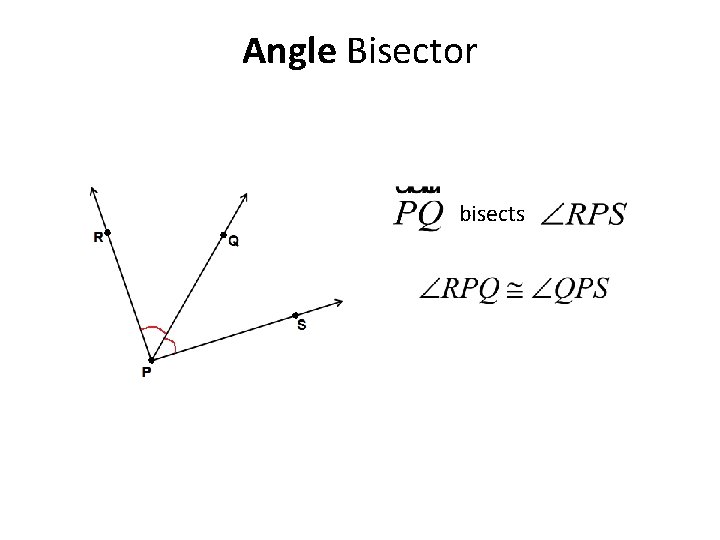
Angle Bisector bisects

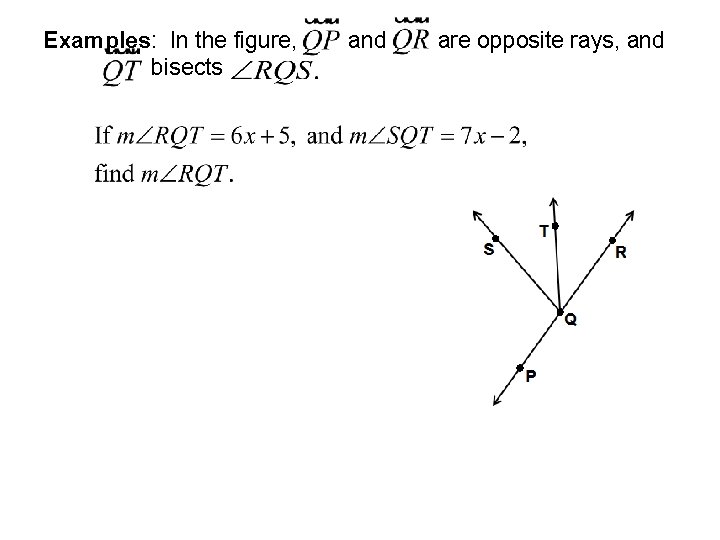
Examples: In the figure, bisects and are opposite rays, and

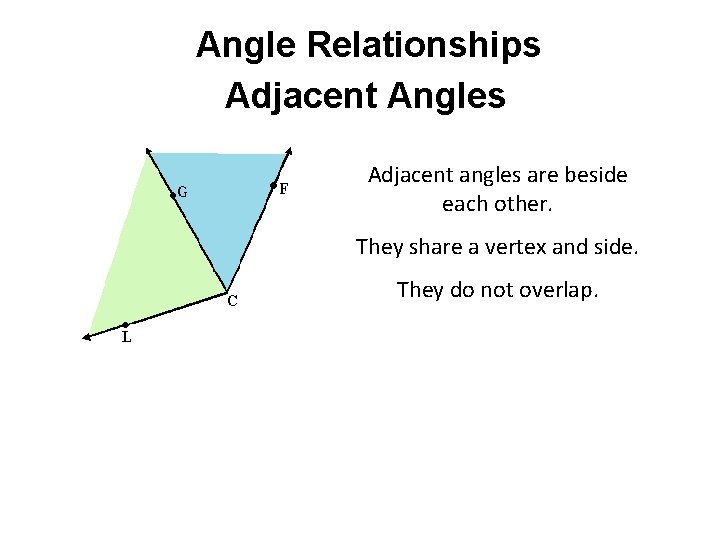
Angle Relationships Adjacent Angles Adjacent angles are beside each other. They share a vertex and side. They do not overlap.

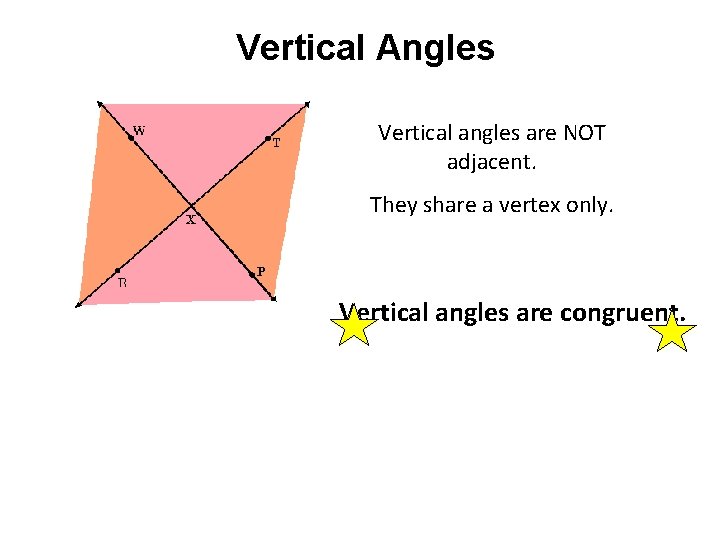
Vertical Angles Vertical angles are NOT adjacent. They share a vertex only. Vertical angles are congruent.

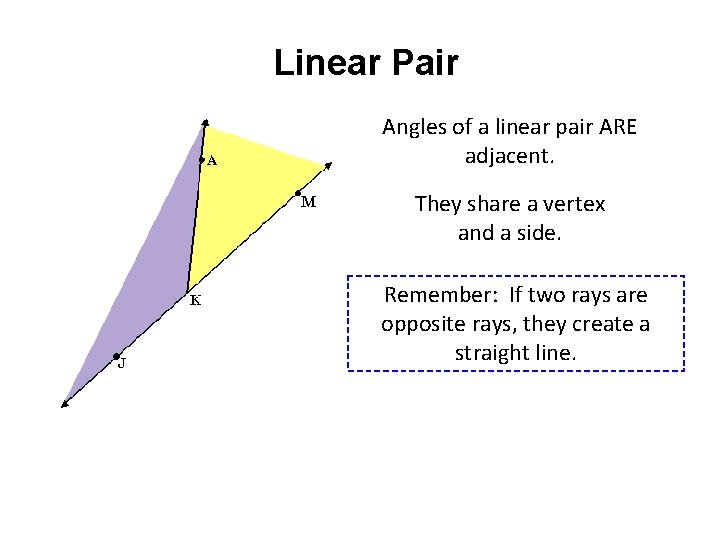
Linear Pair Angles of a linear pair ARE adjacent. They share a vertex and a side. Remember: If two rays are opposite rays, they create a straight line.

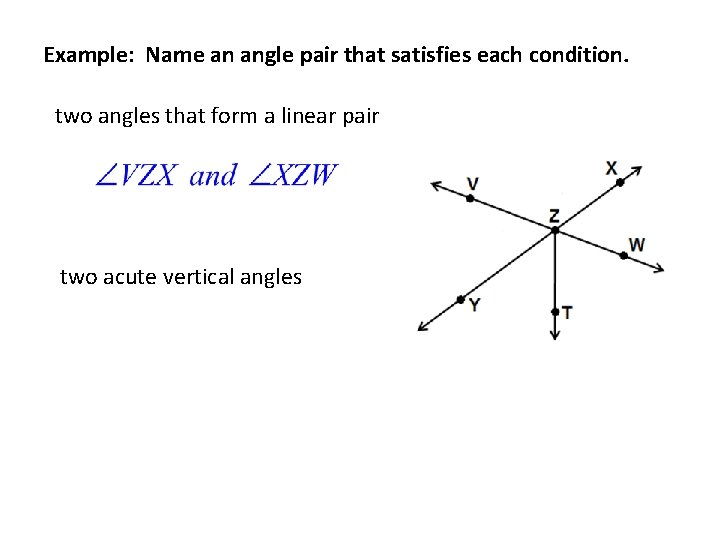
Example: Name an angle pair that satisfies each condition. two angles that form a linear pair two acute vertical angles

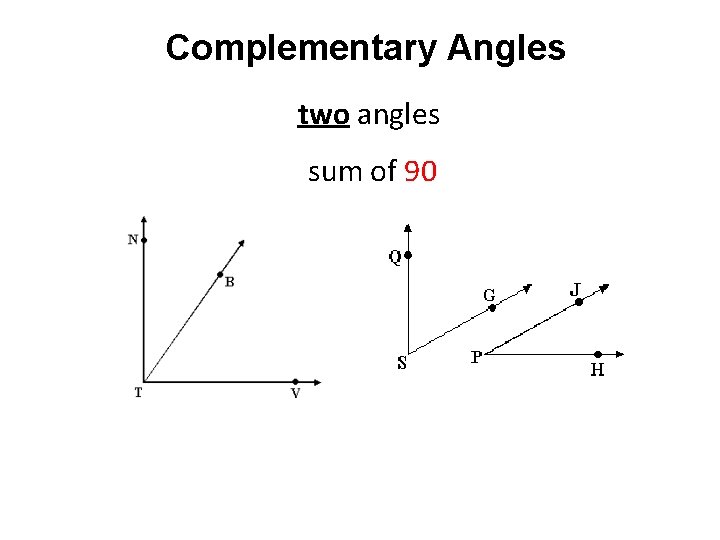
Complementary Angles two angles sum of 90

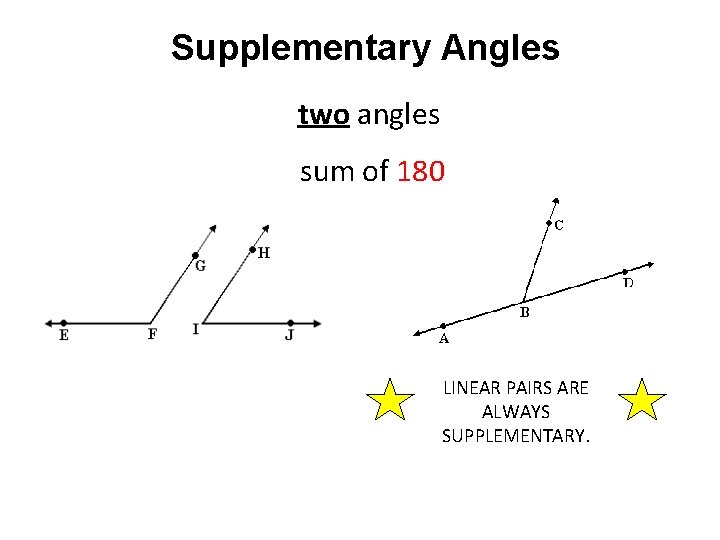
Supplementary Angles two angles sum of 180 LINEAR PAIRS ARE ALWAYS SUPPLEMENTARY.

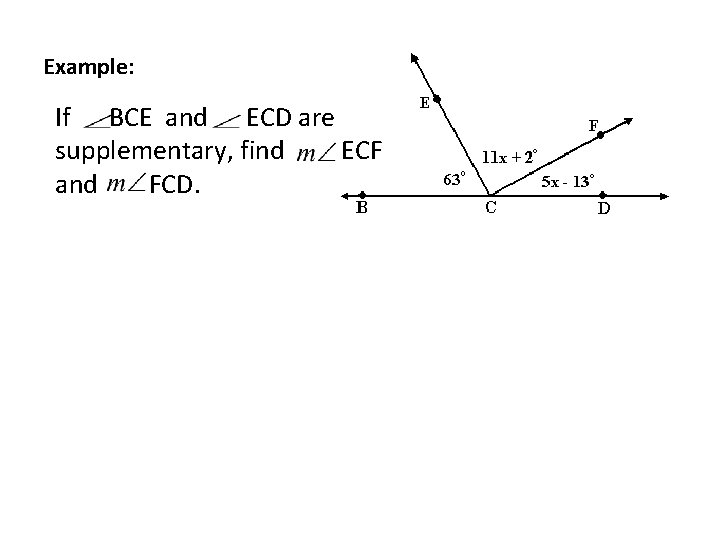
Example: If BCE and ECD are supplementary, find ECF and FCD.

Example: Find the measures of two supplementary angles if the difference in the measures of the two angles is 32. The complement of an angle is 3. 5 times smaller than the supplement of the angle. Find the measure of the angle.

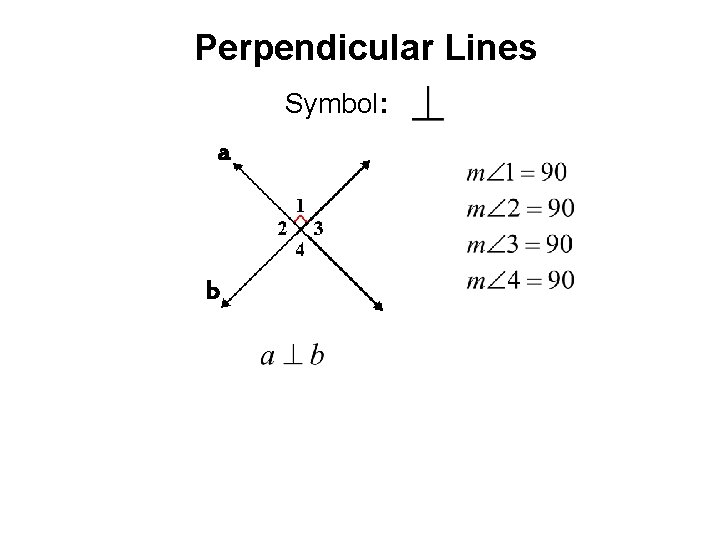
Perpendicular Lines Symbol: a b

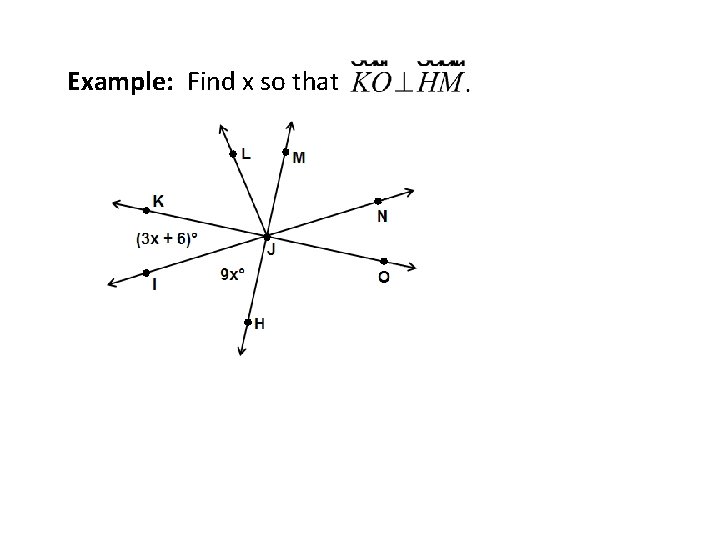
Example: Find x so that