Advanced Geometry Deductive Reasoning Lesson 1 Reasoning and

Advanced Geometry Deductive Reasoning Lesson 1 Reasoning and Conditional Statements

Inductive Reasoning making conclusions based on observations Conjecture similar to a hypothesis in science

Examples: Make a conjecture about the next term in each sequence and then find the term. 160, -80, 40, -20, 10 divide by -2; -5 20, 16, 11, 5, -2, -10

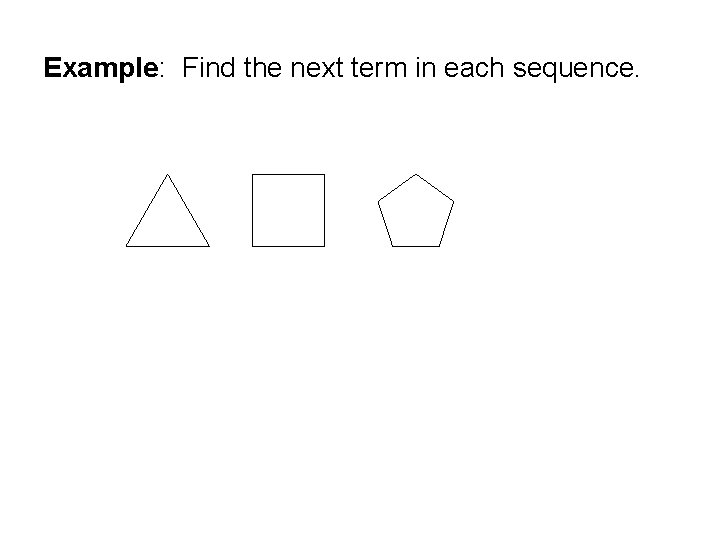
Example: Find the next term in each sequence.

Example: Make a conjecture about the next term in each sequence and then find the term.

Example: Make a conjecture based on the given information. Draw a figure to illustrate your conjecture. Each side of a square measures 3 feet.

Example: Make a conjecture based on the given information. Draw a figure to illustrate your conjecture. and are vertical angles.

Counterexample an example – proves the statement is false Example: Give a counterexample to show that the conjecture is false. Given: Angles 1 and 2 are adjacent angles. Conjecture: Angles 1 and 2 form a linear pair.

Example: Determine whether each conjecture is true or false. Give a counterexample for any false conjecture. Given: All sides of a quadrilateral are 3 inches long. Conjecture: The quadrilateral’s perimeter is 12 inches.

Deductive Reasoning making conclusions based on facts Deductive Reasoning is used to PROVE statements in mathematics. All statements must be justified by: • definitions, • properties, • postulates, OR • theorems

Validity Definition: being deduced or inferred based on facts or evidence Validity and truth are not the same thing. A statement is valid if it follows the rule.

Example: Determine whether the stated conclusion is valid based on the given information. If not, write invalid. Explain your reasoning. If two numbers are odd, then their sum is even. Given: The numbers 3 and 11. Valid Conclusion: The sum is even. Given: The numbers 2 and 7. Conclusion: The sum is even.

Example: Determine whether the stated conclusion is valid based on the given information. If not, write invalid. Explain your reasoning. If two angles are vertical angles, then they are congruent. Given: Conclusion: M and N Invalid: are vertical angles. Given: X and Conclusion: Y are vertical angles

Example: Determine a conclusion that follows from statements (1) and (2). If a valid conclusion does not follow, write no valid conclusion. (1) If n is a natural number, then n is an integer. (2) n is a natural number n is an integer (1) If it is Saturday, then I do not have to go to school. (2) I did not go to school today. no valid conclusion (1) If x = 4, then y = 7. (2) If y = 7, then z = 12.

Conditional Statements Example: If three points are on the same line, then they are collinear. Example (cont. ): DOES NOT INCLUDE IF Hypothesis: three points are on the same line Conclusion: they are collinear DOES NOT INCLUDE THEN

Sometimes a conditional statement is not written in if-then form. Example: Write the statement “Adjacent angles have a common vertex” in if-then form. If two angles are adjacent, then they have a common vertex. Separate the original statement at the verb.

Converse switch the hypothesis and conclusion Original Statement: If two angles are congruent, then they have the same measure. Converse: If two angles have the same measure, then they are congruent.

Example: Write the converse of each conditional. Determine if the converse is true or false. If it is false, give a counterexample. Angles that form a linear pair are supplementary. All squares are rectangles.