Advanced Data Structures Shanwd UNIT III GRAPHS by

Advanced Data Structures Shanwd UNIT III GRAPHS by Shweta 1

Institute & Department Vision Mission Institute Vision : "Satisfy the aspirations of youth force, who want to lead nation towards prosperity through techno-economic development. " Institute Mission : “To provide, nurture and maintain an environment of high academics excellence, research and entrepreneurship for all aspiring students, which will prepare them to face global challenges maintaining high ethical and moral standards. “ Departmental Vision : “Empowering the students to be professionally competent & socially responsible for techno- economic development of society. ” Departmental Mission : A: To provide quality education enabling students for higher studies, research and entrepreneurship B: To inculcate professionalism and ethical values through day to day practices. 2

Objectives v Graphs as one of the most important non-linear data structures v The representation that models various kinds of graphs v Some useful graph algorithms Advanced Data Structures Shanwd by Shweta 3

Introduction v A graph G is a discrete structure consisting of nodes (vertices) and the lines joining the nodes (edges) v For finite graphs, V and E are finite. We can write a graph as G = (V, E) Graph traversals— Visiting all the vertices and edges in a systematic fashion is called as a graph traversal Advanced Data Structures Shanwd by Shweta 4

Introduction v Graphs are classified as directed and undirected graphs v In an undirected graph, an edge is a set of two vertices where order does not make any relevance, whereas in a directed graph, an edge is an ordered pair Advanced Data Structures Shanwd by Shweta 5

Advanced Data Structures Shanwd Graph Abstract Data Type v Graph create() : Graph insert vertex(Graph, v) : Graph delete vertex(Graph, v) : Graph insert edge(Graph, u, v) : Graph delete edge(Graph, u, v) : Graph is empty(Graph) : Boolean; end graph by Shweta 6

Representation of Graphs v v Adjacency matrix (sequential representation) Adjacency list (linked representation) Adjacency Multilist Inverse Adjacency List Advanced Data Structures Shanwd by Shweta 7

Adjacency Matrix v The graphs represented a sequential representation matrices is called an adjacency matrix Advanced Data Structures Shanwd by Shweta 8

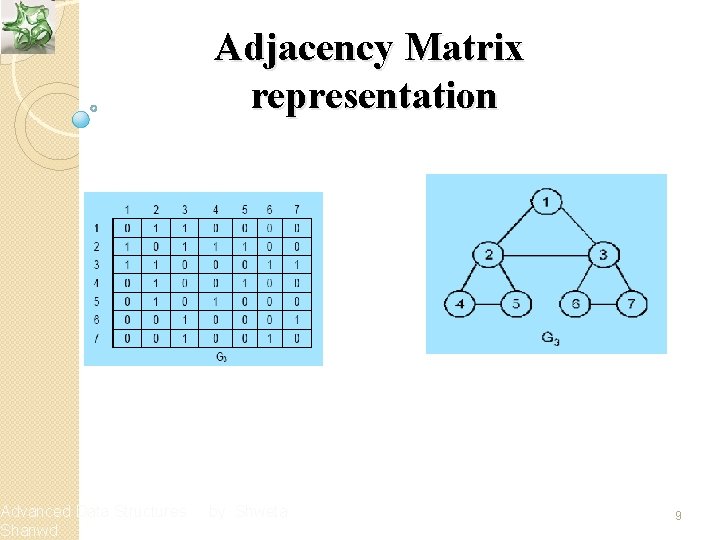
Advanced Data Structures Shanwd Adjacency Matrix representation by Shweta 9

Adjacency Lists v In an adjacency list, the n rows of the adjacency list are represented as n-linked lists, one list per vertex of the graph v We can represent G by an array Head, where Head[i] is a pointer to the adjacency list of vertex i v Each node of the list has at least two fields: vertex and link v The vertex field contains the vertex–id, and link field stores the pointer to the next node storing another vertex adjacent to i Advanced Data Structures Shanwd by Shweta 10

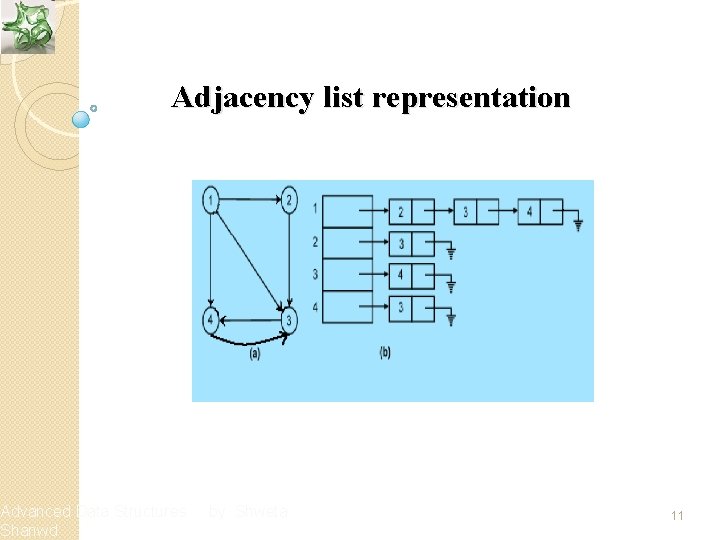
Adjacency list representation Advanced Data Structures Shanwd by Shweta 11

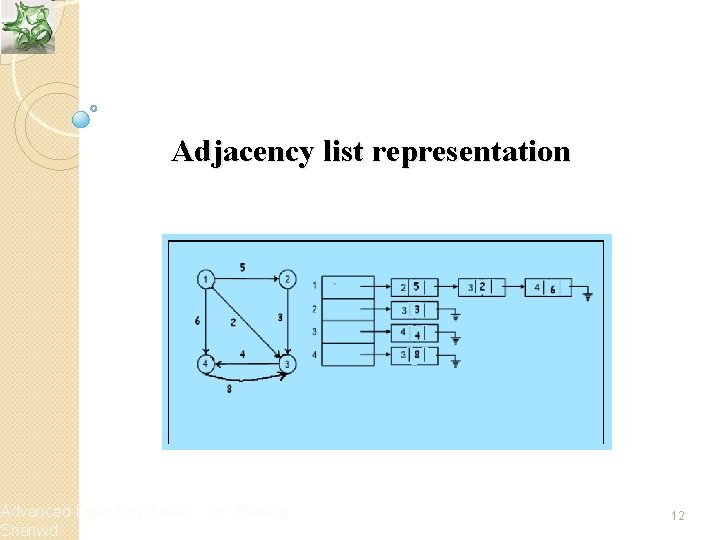
Adjacency list representation Advanced Data Structures Shanwd by Shweta 12

Adjacency Multi-list v Multiclass are lists where nodes may be shared among several other lists Advanced Data Structures Shanwd by Shweta 13

Adjacency Multi-list v The node structure of such a list can be represented as follows : Advanced Data Structures Shanwd by Shweta 14

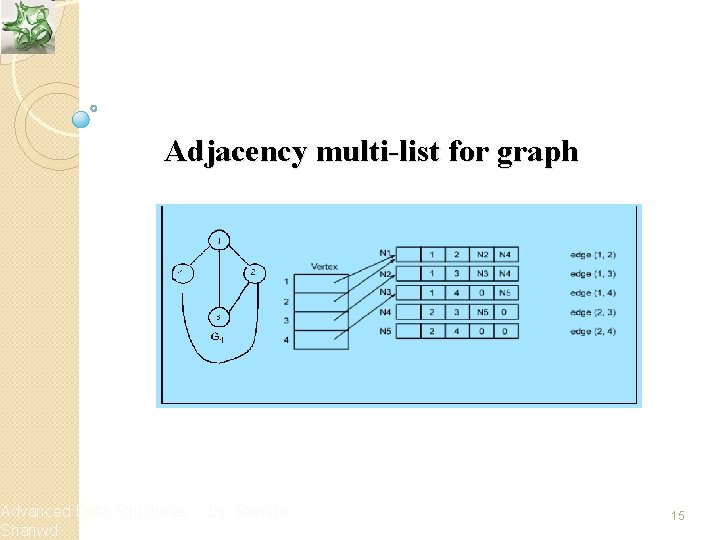
Adjacency multi-list for graph Advanced Data Structures Shanwd by Shweta 15

Inverse Adjacency List v Inverse adjacency lists is a set of lists that contain one list for vertex v Each list contains a node per vertex adjacent to the vertex it represents Advanced Data Structures Shanwd by Shweta 16

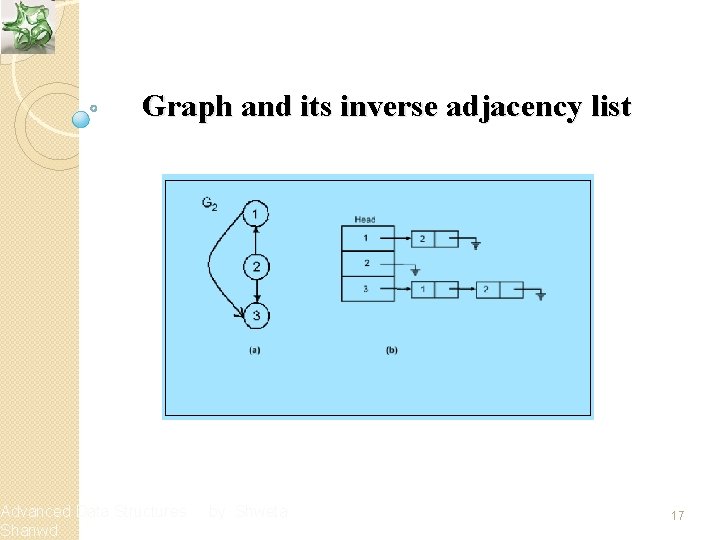
Graph and its inverse adjacency list Advanced Data Structures Shanwd by Shweta 17

Depth-First Search v DFS starts at the vertex v of G as a start vertex and v is marked as visited v Then, each unvisited vertex adjacent to v is searched the DFS recursively v Once all the vertices that can be reached from v have been visited, the search of v is complete v If some vertices remain unvisited, we select an unvisited vertex as a new start vertex and then repeat the process until all the vertices of G are marked visited Advanced Data Structures Shanwd by Shweta 18

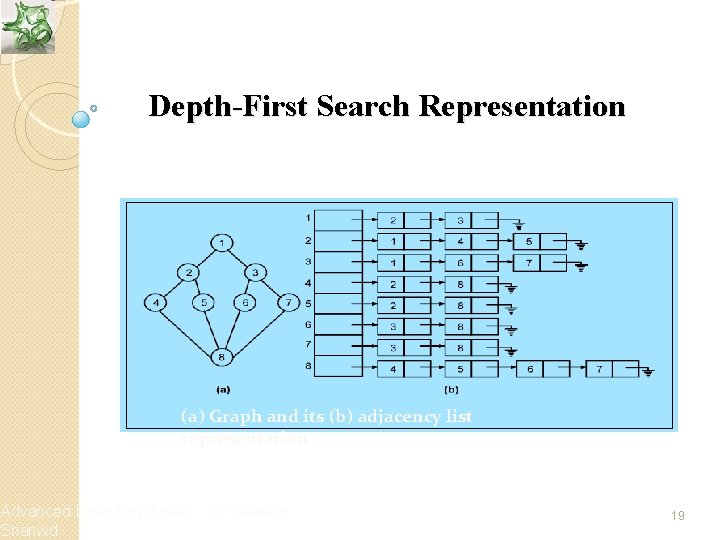
Depth-First Search Representation (a) Graph and its (b) adjacency list representation Advanced Data Structures Shanwd by Shweta 19

Spanning Tree v A tree is a connected graph with no cycles v A spanning tree is a sub-graph of G that has all vertices of G and is a tree v A minimum spanning tree of a weighted graph G is the spanning tree of G whose edges sum to minimum weight Advanced Data Structures Shanwd by Shweta 20

Breadth-First Search v In BFS, all the unvisited vertices adjacent to i are visited after visiting the start vertex i and marking it visited v Next, the unvisited vertices adjacent to these vertices are visited and so on until the entire graph has been traversed Advanced Data Structures Shanwd by Shweta 21

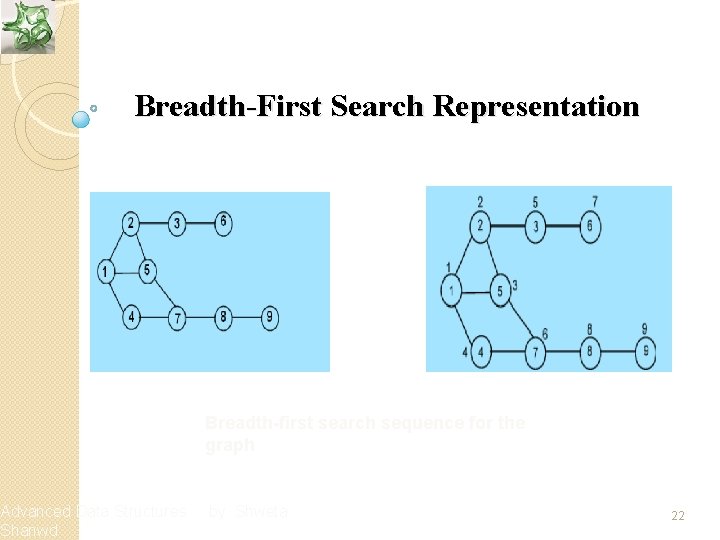
Breadth-First Search Representation Advanced Data Structures Shanwd Breadth-first search sequence for the graph by Shweta 22

Spanning Tree v A tree is a connected graph with no cycles v A spanning tree is a sub-graph of G that has all vertices of G and is a tree v A minimum spanning tree of a weighted graph G is the spanning tree of G whose edges sum to minimum weight Advanced Data Structures Shanwd by Shweta 23

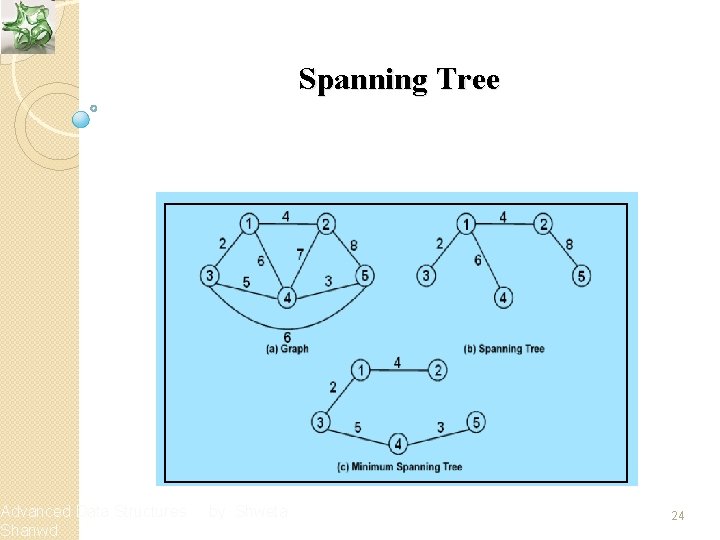
Advanced Data Structures Shanwd Spanning Tree by Shweta 24

Connected Components v An undirected graph is connected if there is at least one path between every pair of vertices in the graph v A connected component of a graph is a maximal connected sub -graph, that is, every vertex in a connected component is reachable from the vertices in the component Advanced Data Structures Shanwd by Shweta 25

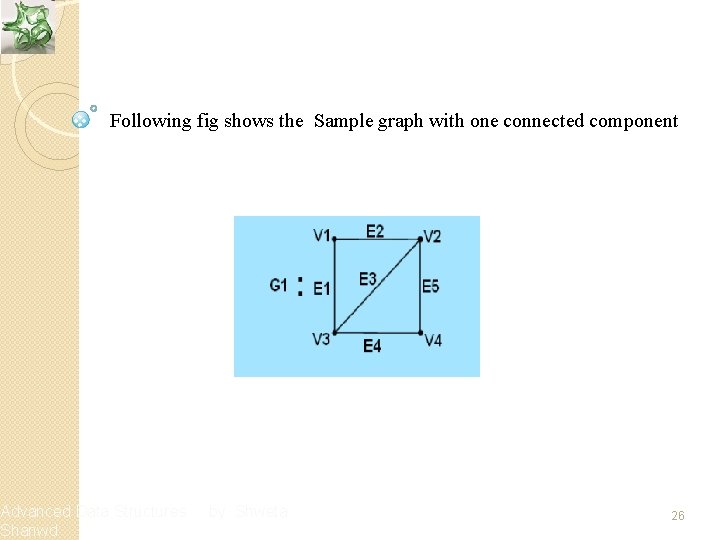
v Following fig shows the Sample graph with one connected component Advanced Data Structures Shanwd by Shweta 26

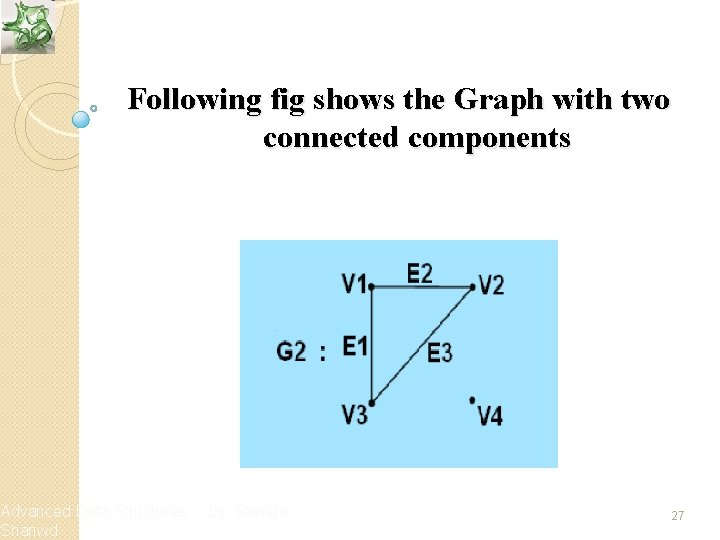
Following fig shows the Graph with two connected components Advanced Data Structures Shanwd by Shweta 27

Prim’s Algorithm v Prim’s algorithm starts from one vertex and grows the rest of the tree by adding one vertex at a time, by adding the associated edges v This algorithm builds a tree by iteratively adding edges until a minimal spanning tree is obtained, that is, when all nodes are added v At each iteration, it adds to the current tree a vertex though minimum weight edge that does not complete a cycle Advanced Data Structures Shanwd by Shweta 28

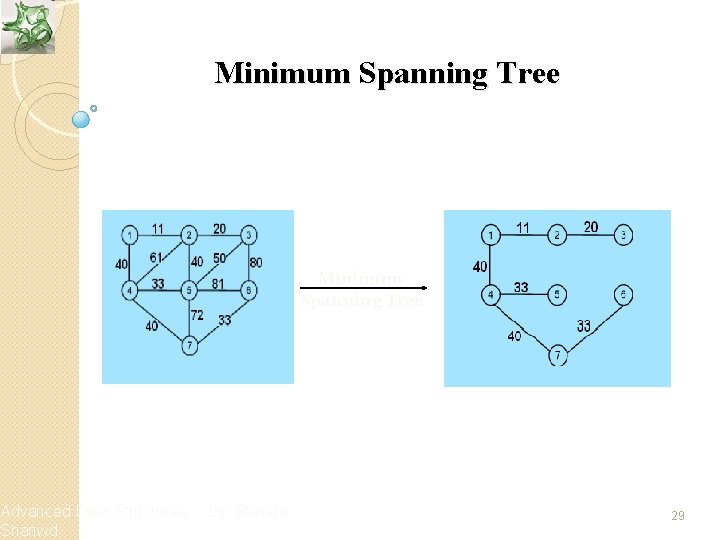
Advanced Data Structures Shanwd Minimum Spanning Tree by Shweta 29

Kruskal’s Algorithm v Another way to construct a minimum spanning tree for a graph G is to start with a graph T = (V′, E′ = ø) consisting of the n vertices of G and having no edges v In Prim’s algorithm, we start with one connected component, add a vertex to have one connected component and no cycles, and end up with one connected component v Here, we start with n connected components; at each step, the number of connected components would reduce by one and end up with one connected component Advanced Data Structures Shanwd by Shweta 30

Shortest Path Algorithm v The shortest path between two given vertices is the path having minimum length v This problem can be solved by one of the greedy algorithms, by Edger W. Dijkstra, often called as Dijkstra’s algorithm Advanced Data Structures Shanwd by Shweta 31

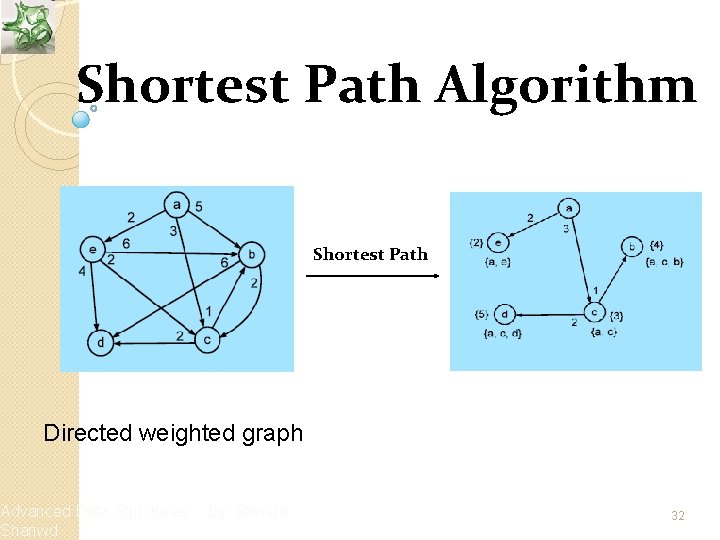
Shortest Path Algorithm Shortest Path Directed weighted graph Advanced Data Structures Shanwd by Shweta 32

Summary v Graphs are one of the most important non-linear data structures. A graph is a representation of relation v Vertices represent elements and edges represent relationships v In other words, a graph is a collection of nodes (vertices) and arcs joining pair of the nodes (edges) v Graphs are classified as directed and undirected graphs. In an undirected graph, an edge is a set of two vertices where order does not make any relevance, whereas in a directed graph, an edge is an ordered pair. Advanced Data Structures Shanwd by Shweta 33

Summary v Graphs are implemented an array or a linked list representation v An adjacency list is a data structure for representing a graph by keeping a list of the neighbor vertices for each vertex v An adjacency matrix is a data structure for representing a graph as a Boolean matrix where 0 means no edge and 1 corresponds to an edge v A minimum spanning tree is a tree, containing all the vertices of a graph, where the total weight of the edges is minimum v The two popularly used algorithms to compute minimum spanning tree are the following: Prim’s and Kruskal’s algorithms v Dijkstra’s algorithm is another common algorithm for graphs to find the shortest path between two vertices of a graph Advanced Data Structures Shanwd by Shweta 34

Advanced Data Structures Shanwd End of UNIT III…! by Shweta 35