Advanced Computer Programming Sort algorithms Sinan AYDIN Sorting

Advanced Computer Programming Sort algorithms Sinan AYDIN

Sorting algorithm Sort algorithms In computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most frequently used orders are numerical order and lexicographical order. Efficient sorting is important for optimizing the efficiency of other algorithms (such as search and merge algorithms) that require input data to be in sorted lists. More formally, the output of any sorting algorithm must satisfy two conditions: • The output is in nondecreasing order (each element is no smaller than the previous element according to the desired total order); • The output is a permutation (a reordering, yet retaining all of the original elements) of the input. Further, the input data is often stored in an array, which allows random access, rather than a list, which only allows sequential access; though many algorithms can be applied to either type of data after suitable modification. https: //en. wikipedia. org/wiki/Sorting_algorithm

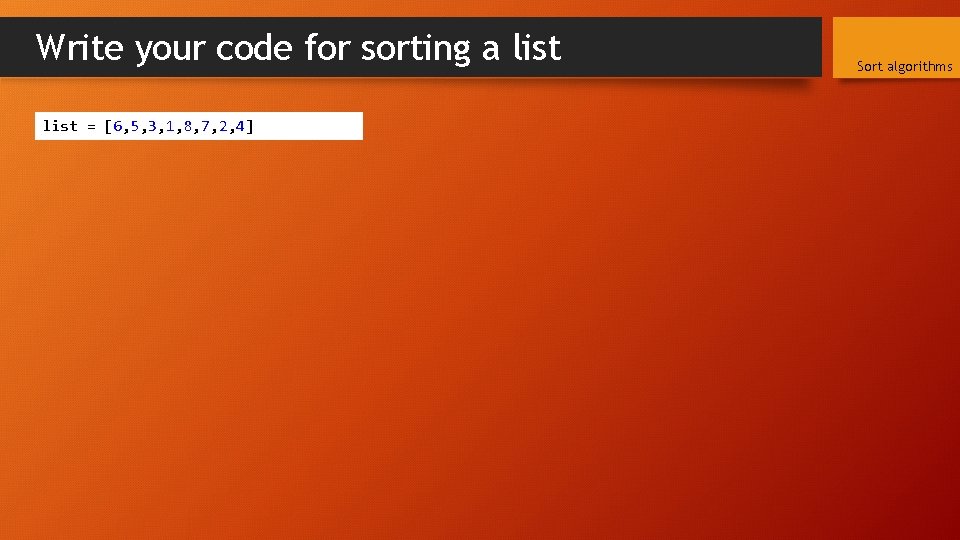
Write your code for sorting a list = [6, 5, 3, 1, 8, 7, 2, 4] Sort algorithms

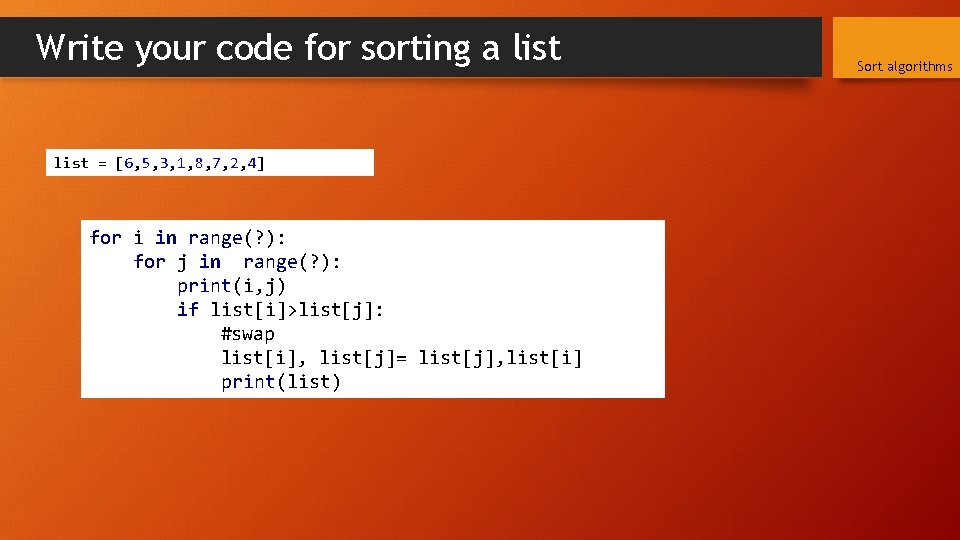
Write your code for sorting a list = [6, 5, 3, 1, 8, 7, 2, 4] for i in range(? ): for j in range(? ): print(i, j) if list[i]>list[j]: #swap list[i], list[j]= list[j], list[i] print(list) Sort algorithms

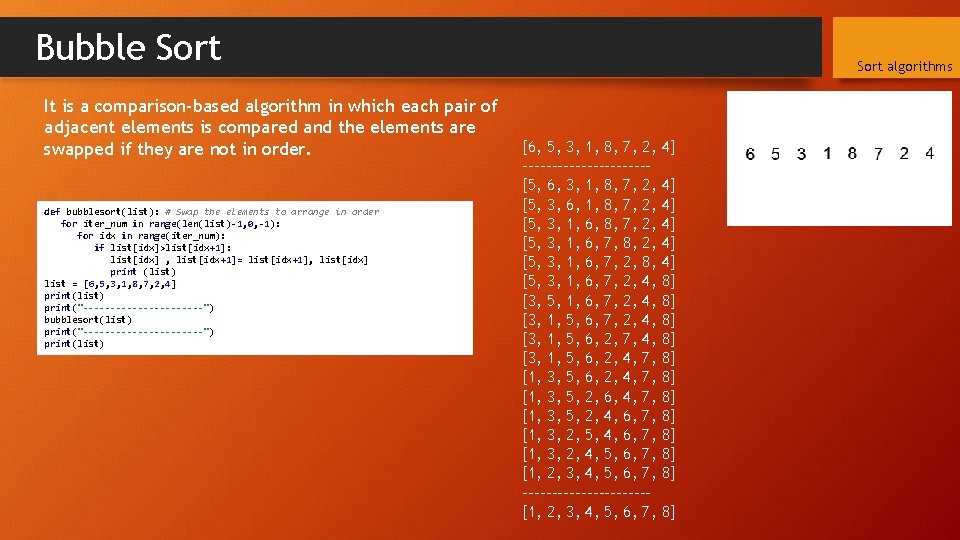
Bubble Sort It is a comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. def bubblesort(list): # Swap the elements to arrange in order for iter_num in range(len(list)-1, 0, -1): for idx in range(iter_num): if list[idx]>list[idx+1]: list[idx] , list[idx+1]= list[idx+1], list[idx] print (list) list = [6, 5, 3, 1, 8, 7, 2, 4] print(list) print("-----------") bubblesort(list) print("-----------") print(list) Sort algorithms [6, 5, 3, 1, 8, 7, 2, -----------[5, 6, 3, 1, 8, 7, 2, [5, 3, 6, 1, 8, 7, 2, [5, 3, 1, 6, 7, 8, 2, [5, 3, 1, 6, 7, 2, 8, [5, 3, 1, 6, 7, 2, 4, [3, 5, 1, 6, 7, 2, 4, [3, 1, 5, 6, 2, 7, 4, [3, 1, 5, 6, 2, 4, 7, [1, 3, 5, 2, 6, 4, 7, [1, 3, 5, 2, 4, 6, 7, [1, 3, 2, 5, 4, 6, 7, [1, 3, 2, 4, 5, 6, 7, [1, 2, 3, 4, 5, 6, 7, -----------[1, 2, 3, 4, 5, 6, 7, 4] 4] 4] 8] 8] 8]

Merge Sort algorithms Merge sort first divides the array into equal halves and then combines them in a sorted manner. def merge_sort(arr): if len(arr) <= 1: # The last array split return arr mid = len(arr) // 2 # Perform merge_sort recursively on both halves left, right = merge_sort(arr[: mid]), merge_sort(arr[mid: ]) # Merge each side together print("Left: " + str(left) + " Right: "+str(right)) return merge(left, right, arr. copy()) def merge(left, right, merged): left_cursor, right_cursor = 0, 0 while left_cursor < len(left) and right_cursor < len(right): # Sort each one and place into the result if left[left_cursor] <= right[right_cursor]: merged[left_cursor + right_cursor] = left[left_cursor] left_cursor += 1 else: merged[left_cursor + right_cursor] = right[right_cursor] right_cursor += 1 for left_cursor in range(left_cursor, len(left)): merged[left_cursor + right_cursor] = left[left_cursor] for right_cursor in range(right_cursor, len(right)): merged[left_cursor + right_cursor] = right[right_cursor] return merged list = [6, 5, 3, 1, 8, 7, 2, 4] print(list) print("-----------") print(merge_sort(list)) [6, 5, 3, 1, 8, 7, 2, 4] -----------Left: [6] Right: [5] Left: [3] Right: [1] Left: [5, 6] Right: [1, 3] Left: [8] Right: [7] Left: [2] Right: [4] Left: [7, 8] Right: [2, 4] Left: [1, 3, 5, 6] Right: [2, 4, 7, 8] [1, 2, 3, 4, 5, 6, 7, 8]

Insertion Sort algorithms Insertion sort involves finding the right place for a given element in a sorted list. So in beginning we compare the first two elements and sort them by comparing them. Then we pick the third element and find its proper position among the previous two sorted elements. This way we gradually go on adding more elements to the already sorted list by putting them in their proper position. def insertion_sort(alist): for i in range(1, len(alist)): j = i-1 nxt_element = alist[i] # Compare the current element with next one while (alist[j] > nxt_element) and (j >= 0): alist[j+1] = alist[j] j=j-1 alist[j+1] = nxt_element print(alist) list = [6, 5, 3, 1, 8, 7, 2, 4] print(list) print("-----------") insertion_sort(list) print("-----------") print(list) [6, 5, 3, 1, 8, 7, 2, -----------[5, 6, 3, 1, 8, 7, 2, [3, 5, 6, 1, 8, 7, 2, [1, 3, 5, 6, 7, 8, 2, [1, 2, 3, 5, 6, 7, 8, [1, 2, 3, 4, 5, 6, 7, -----------[1, 2, 3, 4, 5, 6, 7, 4] 4] 8] 8]

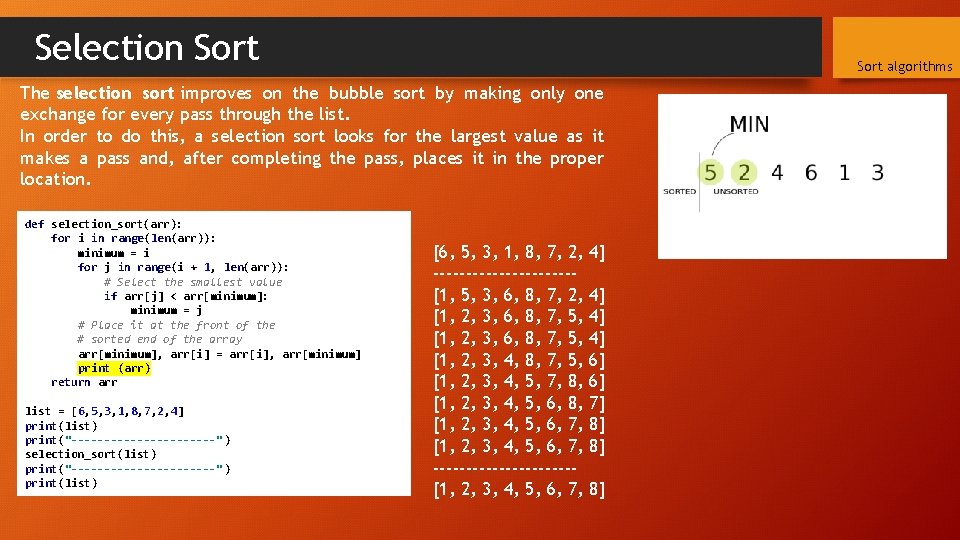
Selection Sort algorithms The selection sort improves on the bubble sort by making only one exchange for every pass through the list. In order to do this, a selection sort looks for the largest value as it makes a pass and, after completing the pass, places it in the proper location. def selection_sort(arr): for i in range(len(arr)): minimum = i for j in range(i + 1, len(arr)): # Select the smallest value if arr[j] < arr[minimum]: minimum = j # Place it at the front of the # sorted end of the array arr[minimum], arr[i] = arr[i], arr[minimum] print (arr) return arr list = [6, 5, 3, 1, 8, 7, 2, 4] print(list) print("-----------") selection_sort(list) print("-----------") print(list) [6, 5, 3, 1, 8, 7, 2, -----------[1, 5, 3, 6, 8, 7, 2, [1, 2, 3, 6, 8, 7, 5, [1, 2, 3, 4, 5, 7, 8, [1, 2, 3, 4, 5, 6, 7, -----------[1, 2, 3, 4, 5, 6, 7, 4] 4] 6] 6] 7] 8] 8] 8]

Quick Sort • The quick sort uses divide and conquer to gain the same advantages as the merge sort, while not using additional storage. • As a trade-off, however, it is possible that the list may not be divided in half. When this happens, we will see that performance is diminished. • A quick sort first selects a value, which is called the pivot value. • Although there are many different ways to choose the pivot value, we will simply use the first item in the list. • The role of the pivot value is to assist with splitting the list. • The actual position where the pivot value belongs in the final sorted list, commonly called the split point, will be used to divide the list for subsequent calls to the quick sort. Sort algorithms

Quick Sort def quick. Sort(alist): quick. Sort. Helper(alist, 0, len(alist)-1) def quick. Sort. Helper(alist, first, last): if first<last: splitpoint = partition(alist, first, last) quick. Sort. Helper(alist, first, splitpoint-1) quick. Sort. Helper(alist, splitpoint+1, last) def partition(alist, first, last): pivotvalue = alist[first] leftmark = first+1 rightmark = last done = False while not done: print(alist) while leftmark <= rightmark and alist[leftmark] <= pivotvalue: leftmark = leftmark + 1 while alist[rightmark] >= pivotvalue and rightmark >= leftmark: rightmark = rightmark -1 if rightmark < leftmark: done = True else: temp = alist[leftmark] = alist[rightmark] = temp = alist[first] print(alist) alist[first] = alist[rightmark] = temp return rightmark list = [6, 5, 3, 1, 8, 7, 2, 4] print(list) print("-----------") quick. Sort(list) print("-----------") print(list) Sort algorithms [6, 5, 3, 1, 8, 7, 2, -----------[6, 5, 3, 1, 8, 7, 2, [6, 5, 3, 1, 4, 2, 7, [2, 5, 3, 1, 4, 6, 7, [2, 1, 3, 5, 4, 6, 7, [1, 2, 3, 5, 4, 6, 7, [1, 2, 3, 4, 5, 6, 7, -----------[1, 2, 3, 4, 5, 6, 7, 4] 4] 8] 8] 8] 8]

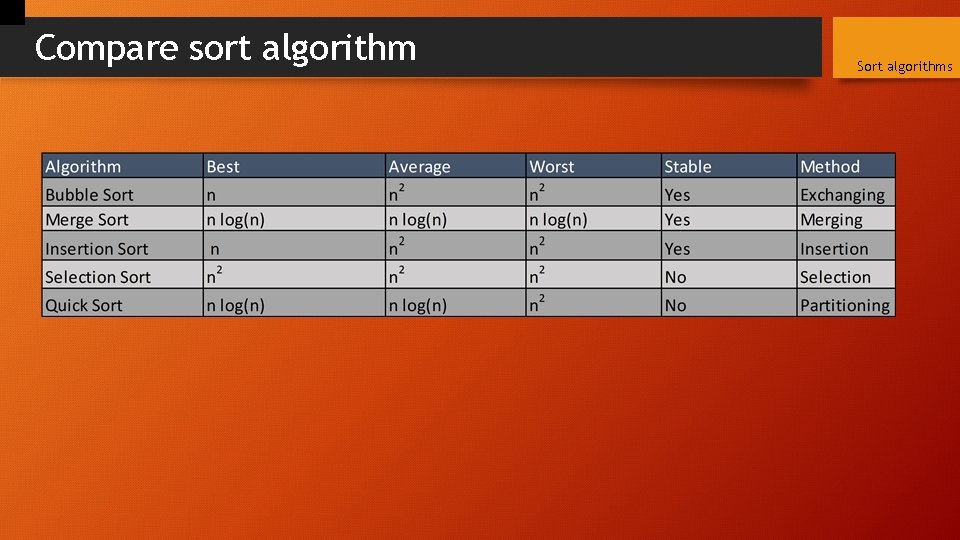
Compare sort algorithm Sort algorithms

Sort visualization https: //www. cs. usfca. edu/~galles/visualization/Comparison. Sort. html https: //visualgo. net/bn/sorting? slide=1 https: //medium. com/@george. seif 94/a-tour-of-the-top-5 -sorting-algorithms-with-python-code 43 ea 9 aa 02889 Sort algorithms