ADVANCED COMPUTER ARCHITECTURE Fundamental Concepts Computing Models Samira

ADVANCED COMPUTER ARCHITECTURE Fundamental Concepts: Computing Models Samira Khan University of Virginia Jan 23, 2019 The content and concept of this course are adapted from CMU ECE 740

AGENDA • Review from last lecture • Fundamental concepts – Computing models • Data flow architecture 2

THE VON NEUMANN MODEL/ARCHITECTURE • Also called stored program computer (instructions in memory). Two key properties: • Stored program – Instructions stored in a linear memory array – Memory is unified between instructions and data • The interpretation of a stored value depends on the control signals When is a value interpreted as an instruction? • Sequential instruction processing – One instruction processed (fetched, executed, and completed) at a time – Program counter (instruction pointer) identifies the current instr. – Program counter is advanced sequentially except for control transfer instructions 3

THE DATA FLOW MODEL (OF A COMPUTER) • Von Neumann model: An instruction is fetched and executed in control flow order – As specified by the instruction pointer – Sequential unless explicit control flow instruction • Dataflow model: An instruction is fetched and executed in data flow order – i. e. , when its operands are ready – i. e. , there is no instruction pointer – Instruction ordering specified by data flow dependence • Each instruction specifies “who” should receive the result • An instruction can “fire” whenever all operands are received – Potentially many instructions can execute at the same time • Inherently more parallel 4

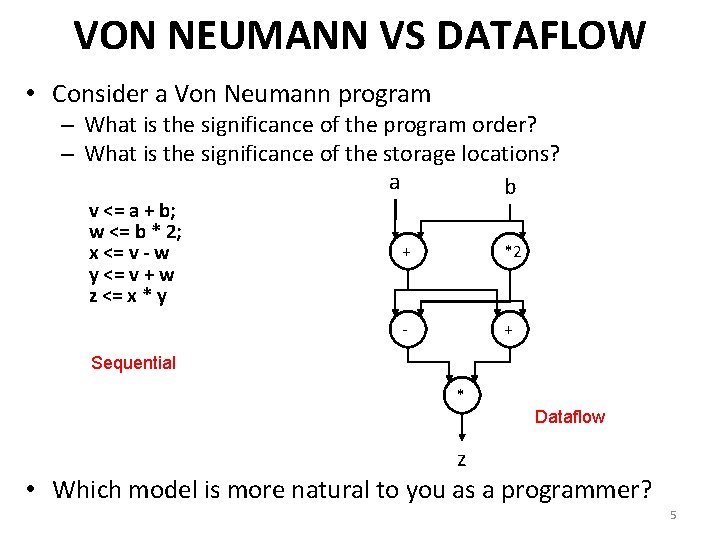
VON NEUMANN VS DATAFLOW • Consider a Von Neumann program – What is the significance of the program order? – What is the significance of the storage locations? a b v <= a + b; w <= b * 2; x <= v - w y <= v + w z <= x * y + *2 - + Sequential * Dataflow z • Which model is more natural to you as a programmer? 5

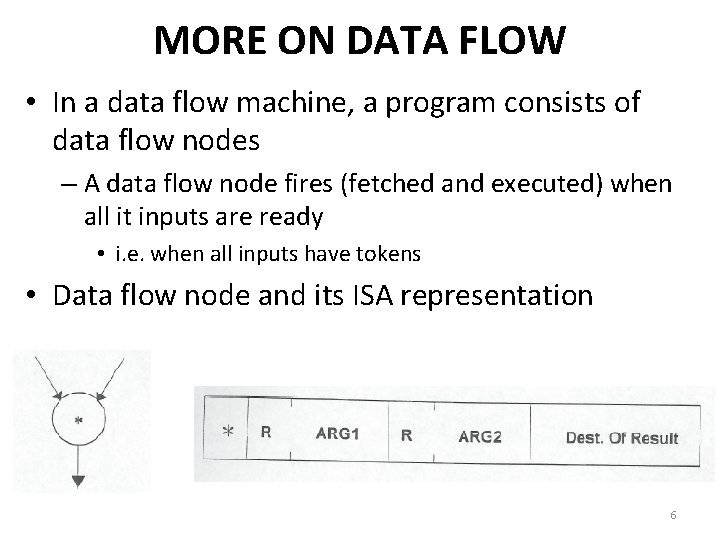
MORE ON DATA FLOW • In a data flow machine, a program consists of data flow nodes – A data flow node fires (fetched and executed) when all it inputs are ready • i. e. when all inputs have tokens • Data flow node and its ISA representation 6

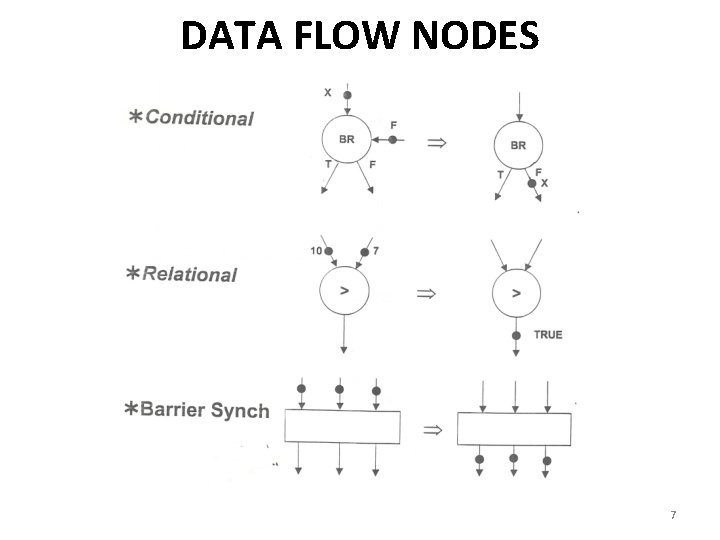
DATA FLOW NODES 7

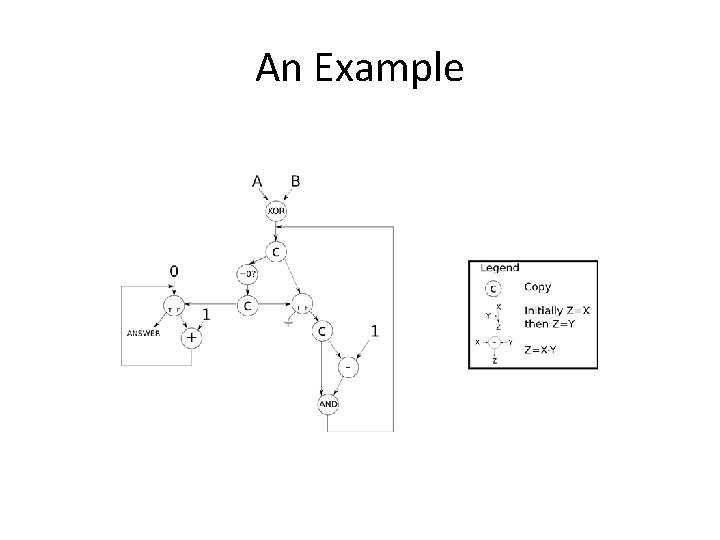
An Example

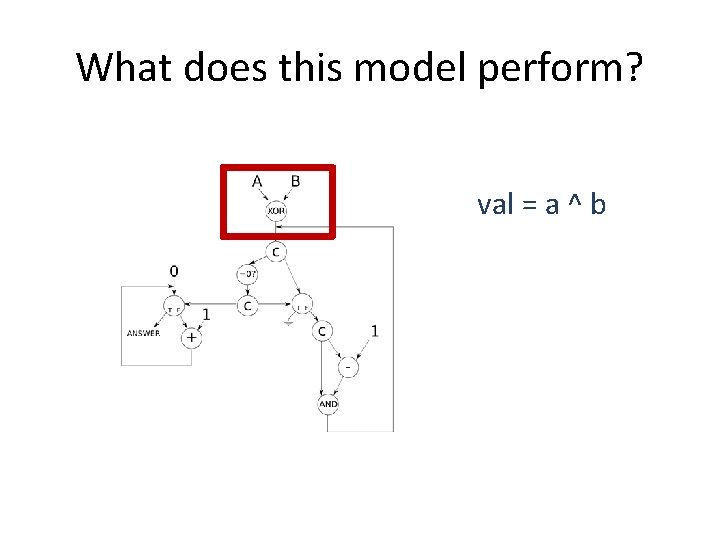
What does this model perform? val = a ^ b

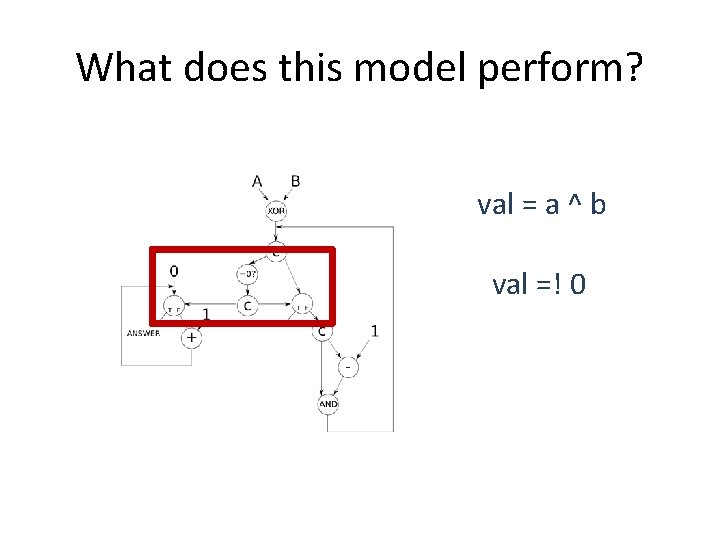
What does this model perform? val = a ^ b val =! 0

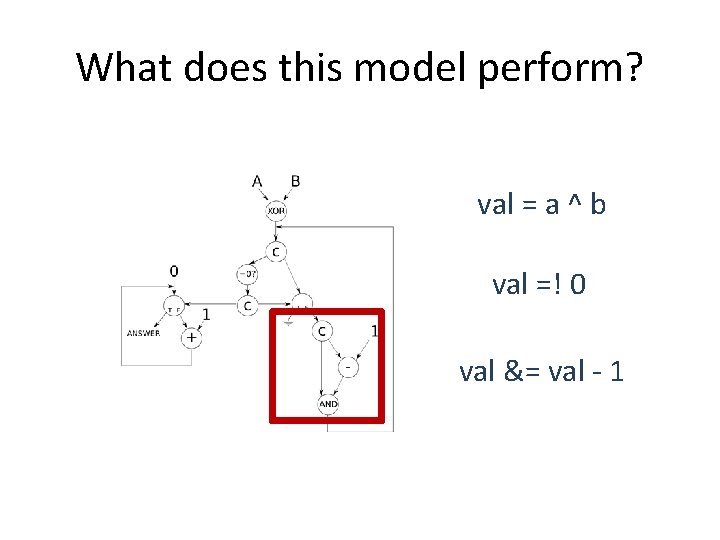
What does this model perform? val = a ^ b val =! 0 val &= val - 1

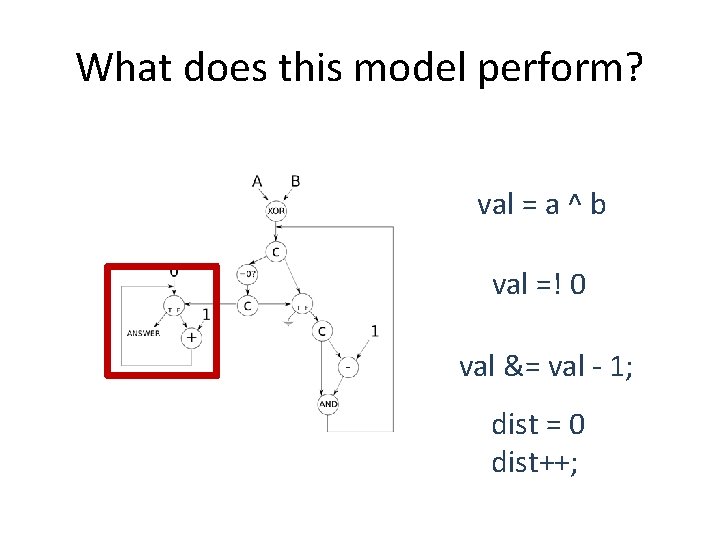
What does this model perform? val = a ^ b val =! 0 val &= val - 1; dist = 0 dist++;

Hamming Distance int hamming_distance (unsigned a, unsigned b) { int dist = 0; unsigned val = a ^ b; // Count the number of bits set while (val != 0) { // A bit is set, so increment the count and clear the bit dist++; val &= val - 1; } // Return the number of differing bits return dist; }

Hamming Distance • Number of positions at which the corresponding symbols are different. • The Hamming distance between: – "karolin" and "kathrin" is 3 – 1011101 and 1001001 is 2 – 2173896 and 2233796 is 3

RICHARD HAMMING • • Best known for Hamming Code Won Turing Award in 1968 Was part of the Manhattan Project Worked in Bell Labs for 30 years • You and Your Research is mainly his advice to other researchers • Had given the talk many times during his life time • http: //www. cs. virginia. edu/~robins/You. And. Your. R esearch. html 15

HOW TO BUILD A DATAFLOW MACHINE? 16

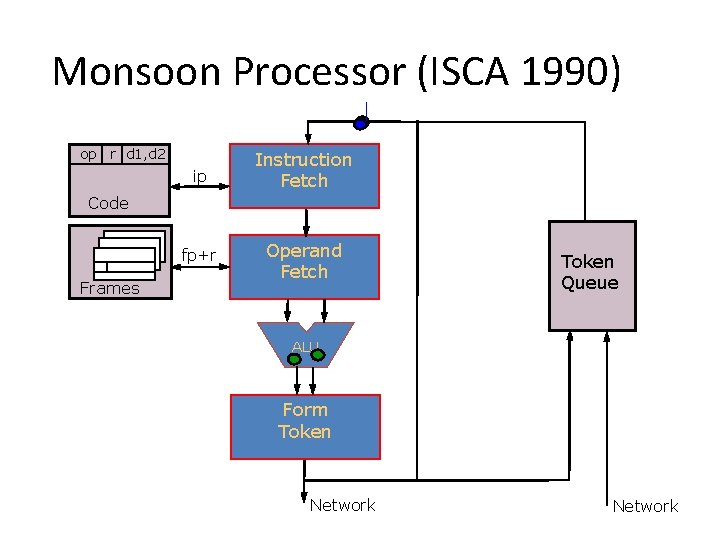
Monsoon Dataflow Processor 1990 17

Review Set 2 • Due Jan 30 • Choose 2 from a set of four • Dennis and Misunas, “A Preliminary Architecture for a Basic Data Flow Processor, ” ISCA 1974. • Arvind and Nikhil, “Executing a Program on the MIT Tagged-Token Dataflow Architecture”, IEEE TC 1990. • H. T. Kung, “Why Systolic Architectures? , ” IEEE Computer 1982. • Annaratone et al. , “Warp Architecture and Implementation, ” ISCA 1986. 18

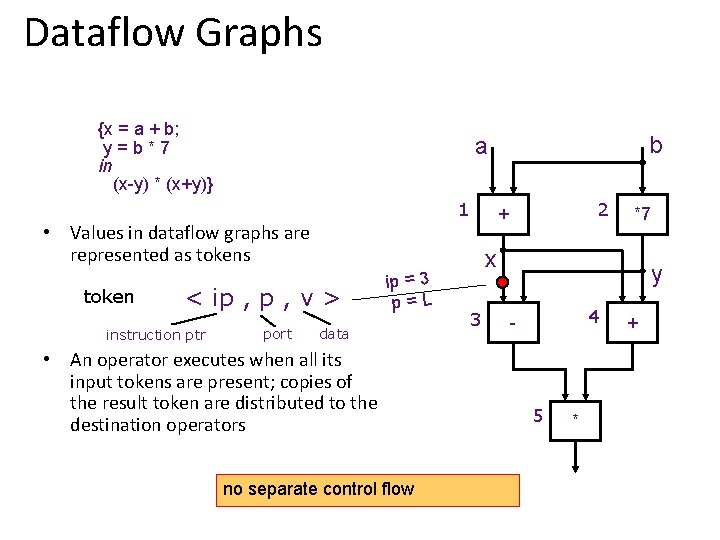
Dataflow Graphs {x = a + b; y=b*7 in (x-y) * (x+y)} 1 < ip , v > instruction ptr port ip = 3 p=L data • An operator executes when all its input tokens are present; copies of the result token are distributed to the destination operators no separate control flow 2 + • Values in dataflow graphs are represented as token b a *7 x 3 y 4 - 5 * +

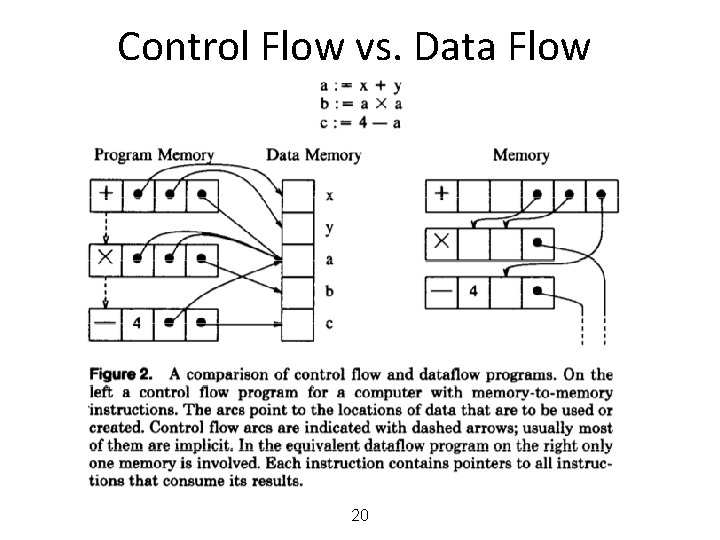
Control Flow vs. Data Flow 20

Static Dataflow • Allows only one instance of a node to be enabled for firing • A dataflow node is fired only when all of the tokens are available on its input arcs and no tokens exist on any of its output arcs • Dennis and Misunas, “A Preliminary Architecture for a Basic Data Flow Processor, ” ISCA 1974. 21

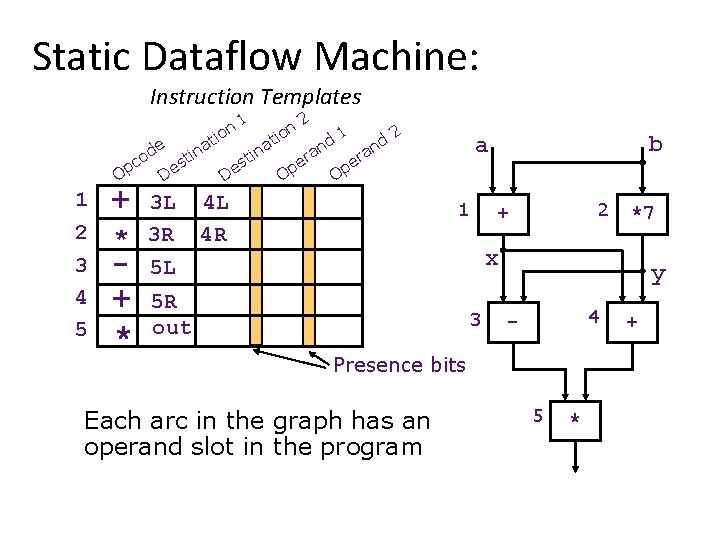
Static Dataflow Machine: Instruction Templates de tin o c s Op De 1 2 3 4 5 + * 3 L 3 R 1 on i at tin s De 2 on Op a er nd 1 nd 2 Op 4 L 4 R b a a er 1 2 + *7 x 5 L 5 R out 3 y 4 - Presence bits Each arc in the graph has an operand slot in the program 5 * +

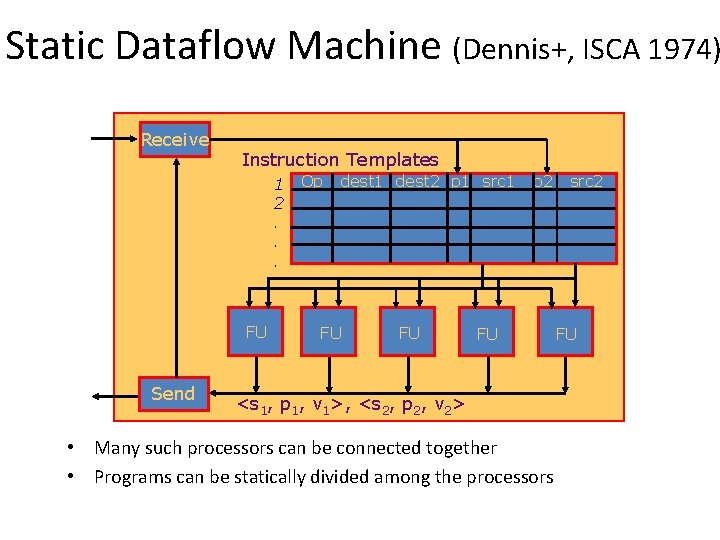
Static Dataflow Machine (Dennis+, ISCA 1974) Receive Instruction Templates 1 2. . . FU Send Op dest 1 dest 2 p 1 src 1 FU FU p 2 FU <s 1, p 1, v 1>, <s 2, p 2, v 2> • Many such processors can be connected together • Programs can be statically divided among the processors src 2 FU

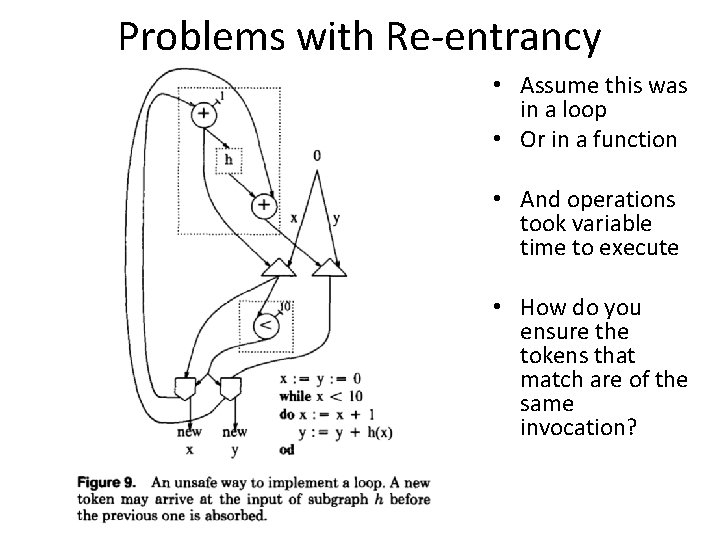
Static Data Flow Machines • Mismatch between the model and the implementation – The model requires unbounded FIFO token queues per arc but the architecture provides storage for one token per arc – The architecture does not ensure FIFO order in the reuse of an operand slot • The static model does not support – Reentrant code • Function calls • Loops – Data Structures 24

Problems with Re-entrancy • Assume this was in a loop • Or in a function • And operations took variable time to execute • How do you ensure the tokens that match are of the same invocation? 25

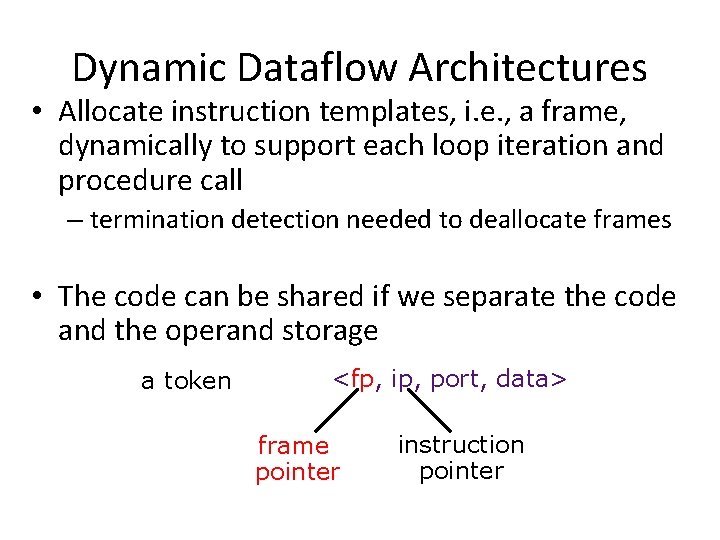
Dynamic Dataflow Architectures • Allocate instruction templates, i. e. , a frame, dynamically to support each loop iteration and procedure call – termination detection needed to deallocate frames • The code can be shared if we separate the code and the operand storage a token <fp, ip, port, data> frame pointer instruction pointer

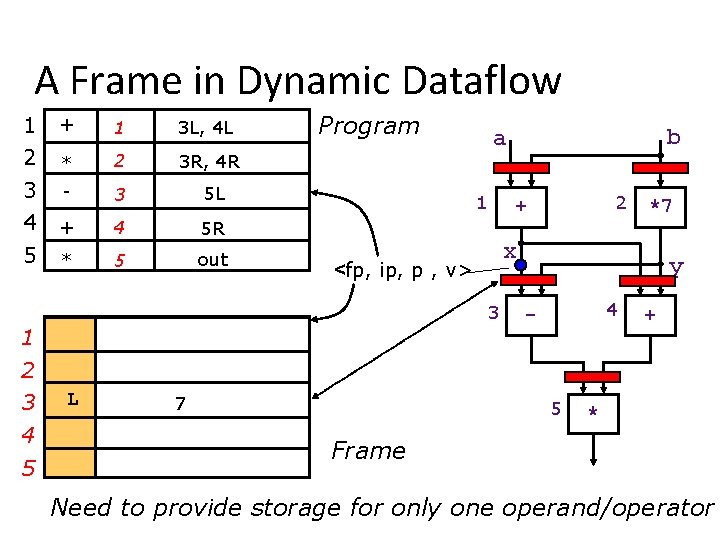
A Frame in Dynamic Dataflow 1 2 + 1 3 L, 4 L * 2 3 R, 4 R 3 4 5 - 3 5 L + 4 5 R * 5 out Program 1 4 5 L 7 *7 x 3 2 + <fp, ip, p , v> 1 b a y 4 - 5 + * Frame Need to provide storage for only one operand/operator

Monsoon Processor (ISCA 1990) op r d 1, d 2 ip Instruction Fetch fp+r Operand Fetch Code Frames Token Queue ALU Form Token Network

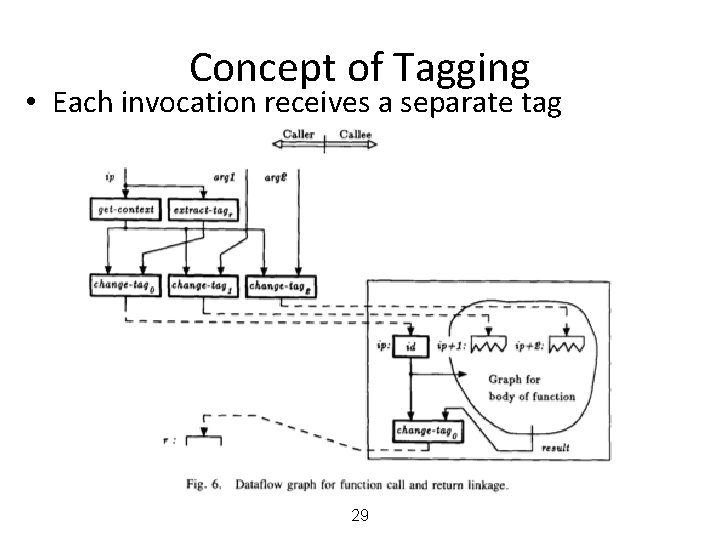
Concept of Tagging • Each invocation receives a separate tag 29

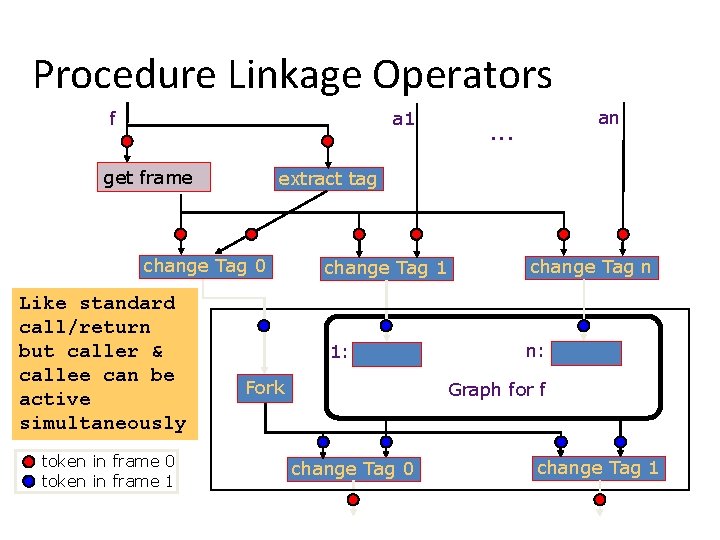
Procedure Linkage Operators f a 1 get frame extract tag change Tag 0 Like standard call/return but caller & callee can be active simultaneously token in frame 0 token in frame 1 an . . . change Tag 1 change Tag n 1: n: Fork Graph for f change Tag 0 change Tag 1

ADVANCED COMPUTER ARCHITECTURE Fundamental Concepts: Computing Models Samira Khan University of Virginia Jan 23, 2019 The content and concept of this course are adapted from CMU ECE 740