Advanced Compilers CMPSCI 710 Spring 2003 Dominators etc

Advanced Compilers CMPSCI 710 Spring 2003 Dominators, etc. Emery Berger University of Massachusetts, Amherst UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE

Dominators, etc. n Last time n Live variable analysis n n Constant propagation n backwards problem algorithms def-use chains Today n n SSA-form dominators UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 2

Def-Use Chains: Problem switch case case n (j) x: i y: i z: i (k) x: a y: b z: c à 1; break; à 2; break; à 3; break; à i; break; worst-case size of graph = O(D*U) = O(N 2) UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 3

SSA Form n Static single assignment n n n Ø each assignment to variable gets unique name all uses reached by that assignment are renamed exactly one def per use sparse program representation: use-def chain = (variable, [use 1, use 2…]) UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 4

SSA Transformations n New variable for each assignment, rename uses v 1 Ã Ã v 2 Ã Ã n 4 v+5 v 1+5 6 v+7 v 2+7 Easy for straight-line code, but what about control flow? UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 5

-Functions n At each join, add special assignment: “ function”: n n n operands indicate which assignments reach join jth operand = jth predecessor If control reaches join from jth predecessor, then value of (R, S, …) is value of jth operand UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 6

SSA Transformation, function if P then v à 4 else v à 6 /* use v */ if P then v 1 à 4 else v 2 à 6 v 3 à (v 1, v 2) /* use v 3 */ UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 7

SSA Example II v à 1 while (v < 10) v à v + 1 1: v à 1 2: if (v < 10) 3: v à v + 1 4: goto 2 UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 8

SSA Example III switch case case (j) x: i y: i z: i (k) x: a y: b z: c à 1; break; à 2; break; à 3; break; à i; break; UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 9

Placing functions n n Safe to put functions for every variable at every join point But: n n n inefficient – not necessarily sparse! loses information Goal: minimal nodes, subject to need UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 10

Function Requirement n Node Z needs function for V if: n n Z is convergence point for two paths originating at different nodes both originating nodes contain assignments to V or also need functions for V v=1 v=2 Z v 1 = 1 v 2 = 2 v 3= (v 1, v 2) Z UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 11

Minimal Placement of functions n n Naïve computation of need is expensive: must examine all triples in graph Can be done in O(N) time n n Relies on dominance frontier computation [Cytron et al. , 1991] Also can be used to compute control dependence graph UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 12

Control Dependence Graph n n Identifies conditions affecting statement execution Statement is control dependent on branch if: n n one edge from branch definitely causes statement to execute another edge can cause statement to be skipped UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 13

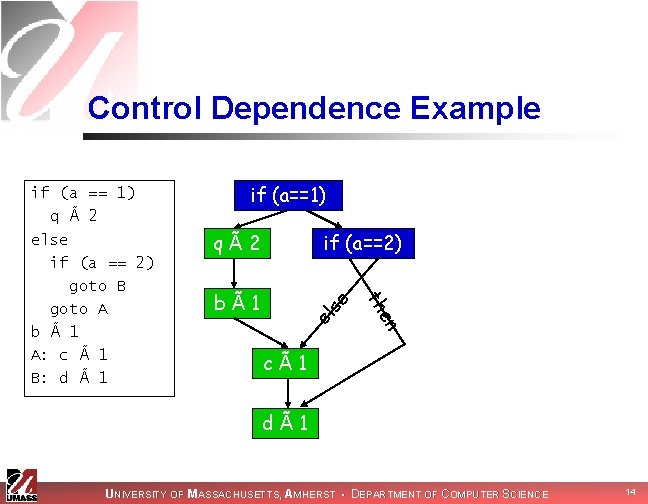
Control Dependence Example if (a==1) el en bÃ1 if (a==2) se qÃ2 th if (a == 1) q à 2 else if (a == 2) goto B goto A b à 1 A: c à 1 B: d à 1 cÃ1 dÃ1 UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 14

Dominators n n Before we do dominance frontiers, we need to discuss other dominance relationships x dominates y (x dom y) n n n in CFG, all paths to y go through x Dom(v) = set of all vertices that dominate v Entry dominates every vertex n n Reflexive: a dom a Transitive: a dom b, b dom c ! a dom c Antisymmetric: a dom b, b dom a ! b=a Notice: in SSA form, a definition dominates its use UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 15

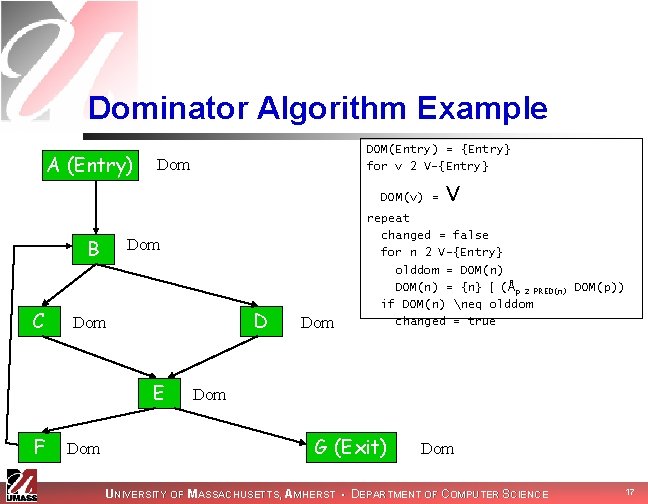
Finding Dominators n n Dom(v) = {v} Åp 2 PRED(v) Dom(p) Algorithm: DOM(Entry) = {Entry} for v 2 V-{Entry} DOM(v) = V repeat changed = false for n 2 V-{Entry} olddom = DOM(n) = {n} [ (Åp if DOM(n) olddom changed = true 2 PRED(n) DOM(p)) UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 16

Dominator Algorithm Example A (Entry) DOM(Entry) = {Entry} for v 2 V-{Entry} Dom DOM(v) = B C Dom D Dom E F Dom V repeat changed = false for n 2 V-{Entry} olddom = DOM(n) = {n} [ (Åp 2 PRED(n) DOM(p)) if DOM(n) neq olddom changed = true Dom G (Exit) Dom UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 17

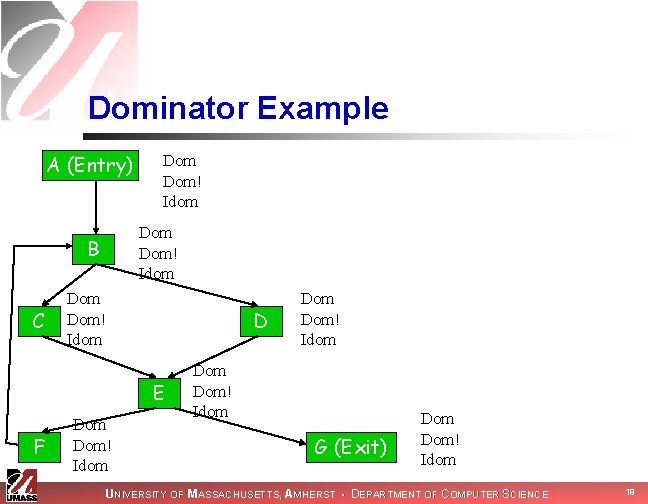
Other Dominators n Strict dominators n n n Dom!(v) = Dom(v) – {v} antisymmetric & transitive Immediate dominator n n Idom(v) = closest strict dominator of v d Idom v if d Dom! v and 8 w 2 Dom!(v): w Dom d antisymmetric Idom induces tree UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 18

Dominator Example A (Entry) Dom! Idom B C Dom Dom! Idom D E F Dom Dom! Idom G (Exit) Dom! Idom UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 19

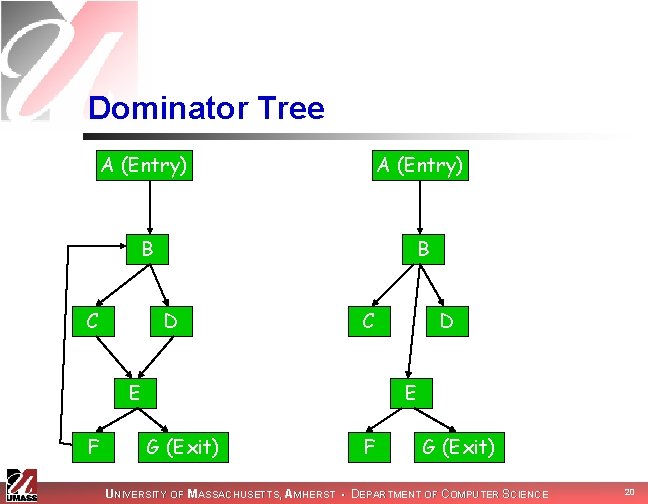
Dominator Tree A (Entry) B B C D C E F D E G (Exit) F G (Exit) UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 20

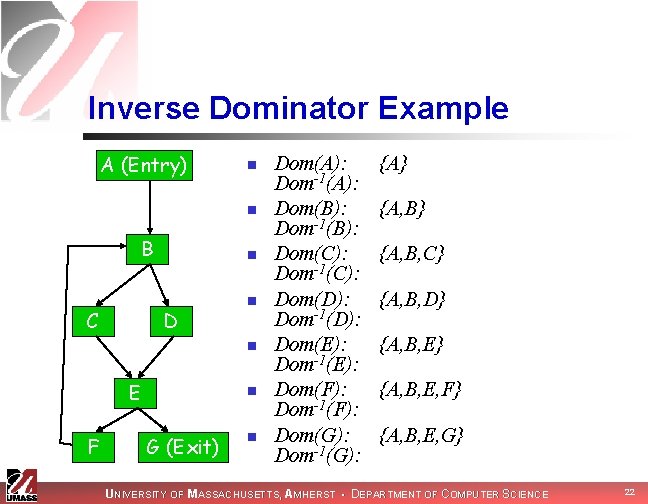
Inverse Dominators n n Dom-1(v) = set of all vertices dominated by v reflexive, antisymmetric, transitive UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 21

Inverse Dominator Example A (Entry) n n B C n D n n E F n G (Exit) n Dom(A): Dom-1(A): Dom(B): Dom-1(B): Dom(C): Dom-1(C): Dom(D): Dom-1(D): Dom(E): Dom-1(E): Dom(F): Dom-1(F): Dom(G): Dom-1(G): {A} {A, B, C} {A, B, D} {A, B, E, F} {A, B, E, G} UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 22

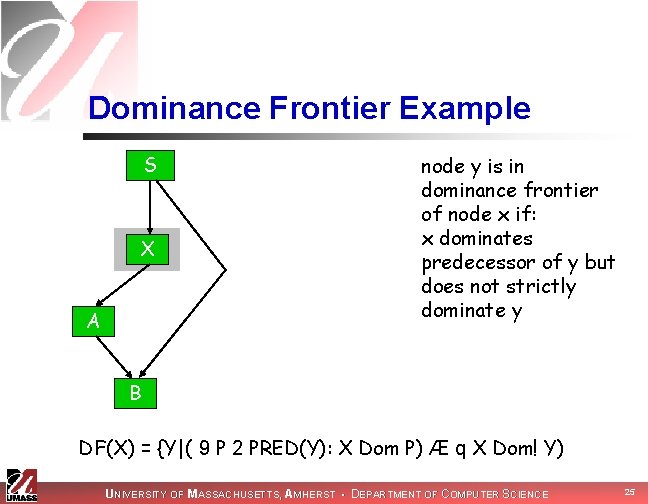
Finally: Dominance Frontiers! n The dominance frontier DF(X) is set of all nodes Y such that: n n X dominates a predecessor of Y But X does not strictly dominate Y n DF(X) = {Y|(9 P 2 PRED(Y): X Dom P) Æ q X Dom! Y) UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 23

Why Dominance Frontiers n Dominance frontier criterion: n n if node x contains def of a, then any node z in DF(x) needs a function for a intuition: at least two non-intersecting paths converge to z, and one path must contain node strictly dominated by x UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 24

Dominance Frontier Example S X A node y is in dominance frontier of node x if: x dominates predecessor of y but does not strictly dominate y B DF(X) = {Y|( 9 P 2 PRED(Y): X Dom P) Æ q X Dom! Y) UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 25

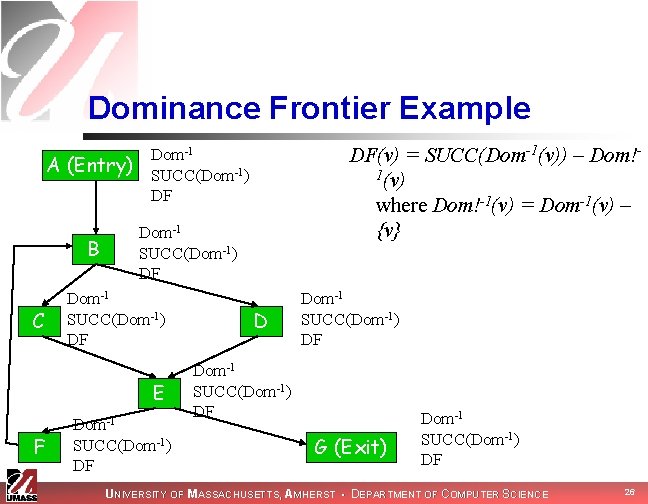
Dominance Frontier Example DF(v) = SUCC(Dom-1(v)) – Dom!1(v) where Dom!-1(v) = Dom-1(v) – {v} Dom-1 A (Entry) SUCC(Dom-1) DF B C Dom-1 SUCC(Dom-1) DF E F Dom-1 SUCC(Dom-1) DF G (Exit) Dom-1 SUCC(Dom-1) DF UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 26

Next Time n n Computing dominance frontiers Computing SSA form UNIVERSITY OF MASSACHUSETTS, AMHERST • DEPARTMENT OF COMPUTER SCIENCE 27