Advanced Algorithms Note print these slides in color

Advanced Algorithms Note: print these slides in color 240 -426 , Semester 1, 2021 -2022 8. Max. Flow Describe the maxflow problem, explain the Ford. Fulkerson and Edmonds-Karp algorithms. Look at the mincut problem, bipartite matching and edge disjoint paths Adv. Algs: 8. Max. Flow 1

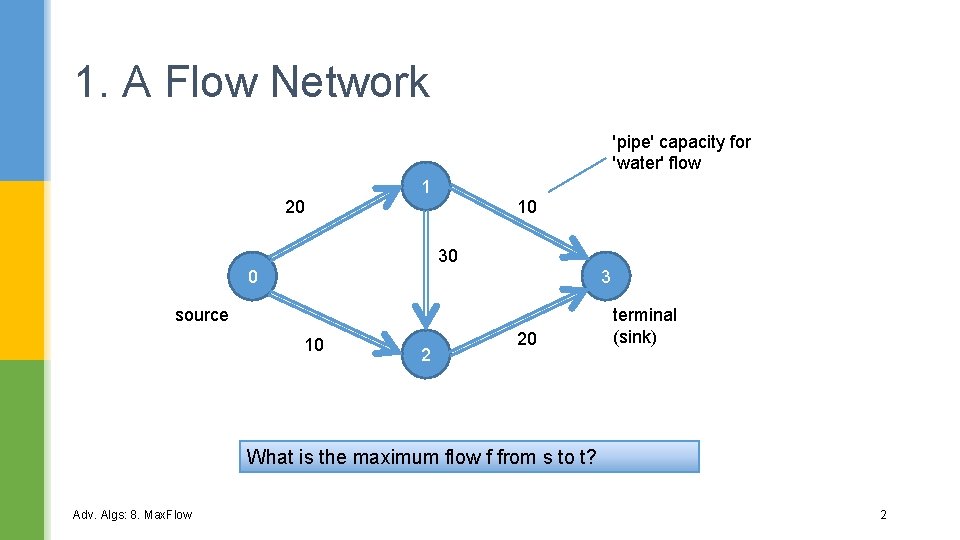
1. A Flow Network 'pipe' capacity for 'water' flow 1 10 20 30 0 3 source 10 2 20 terminal (sink) What is the maximum flow f from s to t? Adv. Algs: 8. Max. Flow 2

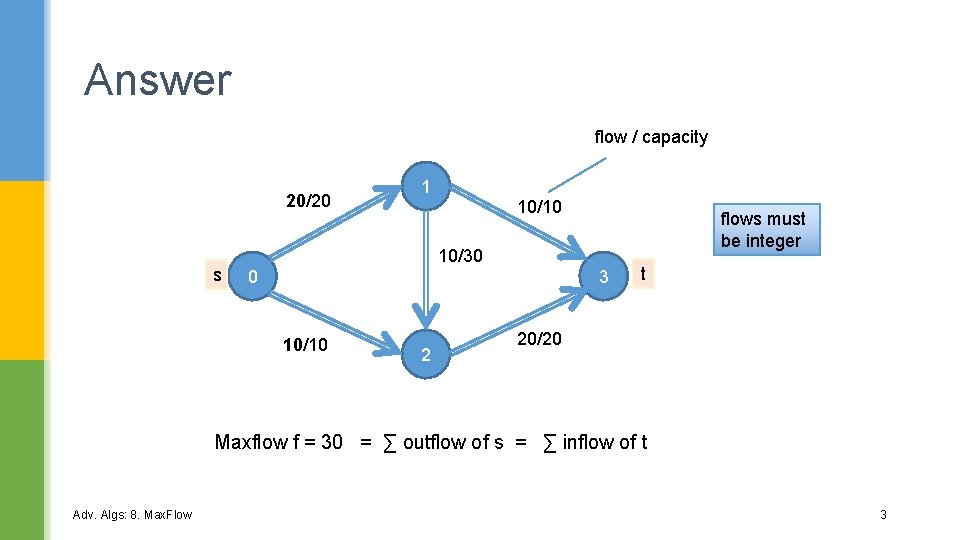
Answer flow / capacity 20/20 s 1 10/10 flows must be integer 10/30 0 3 10/10 2 t 20/20 Maxflow f = 30 = ∑ outflow of s = ∑ inflow of t Adv. Algs: 8. Max. Flow 3

Flow Rules § Capacity constraint 0 ≤ edge's flow ≤ edge's capacity § Flow conservation inflow = outflow at every vertex (except s and t) inflow at v = 5 + 0 = 10 outflow at v = 10 + 0 = 10 Adv. Algs: 8. Max. Flow 4

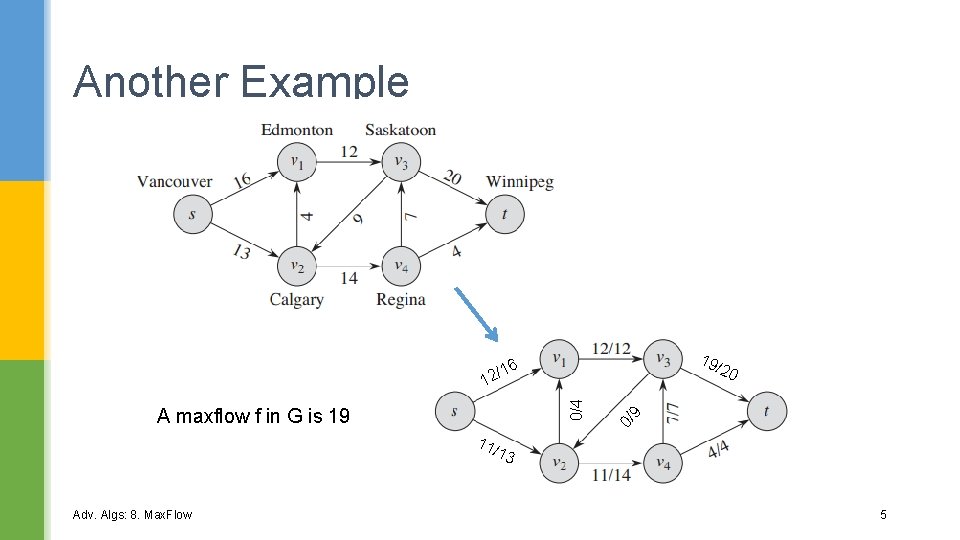
Another Example 19/ 20 A maxflow f in G is 19 11/ Adv. Algs: 8. Max. Flow 0/ 9 0/4 /16 12 13 5

Many Applications of Maxflow § Bipartite matching § Data mining § Network reliability § Image processing § Network connectivity § Distributed computing § many more. . . blood flow analysis

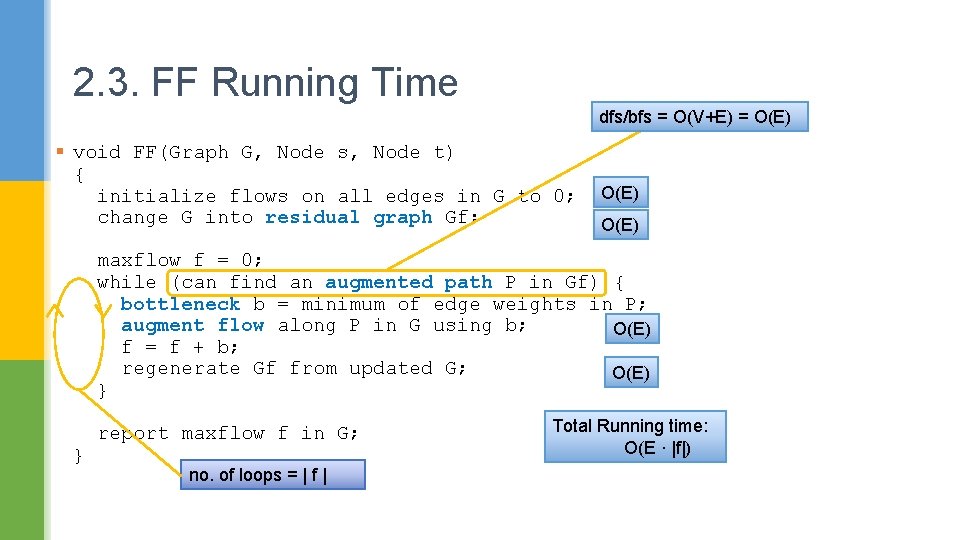
2. Ford-Fulkerson (FF) Algorithm § void FF(Graph G, Node s, Node t) { initialize flows on all edges in G to 0; change G into residual graph Gf; Two graphs G and Gf maxflow f = 0; while (can find an augmented path P in Gf) { bottleneck b = minimum of edge weights in P; augment flow along P in G using b; f = f + b; regenerate Gf from updated G; } } report maxflow f in G; // sum of all bottlenecks Running time: O(E*|f|) Adv. Algs: 8. Max. Flow 7

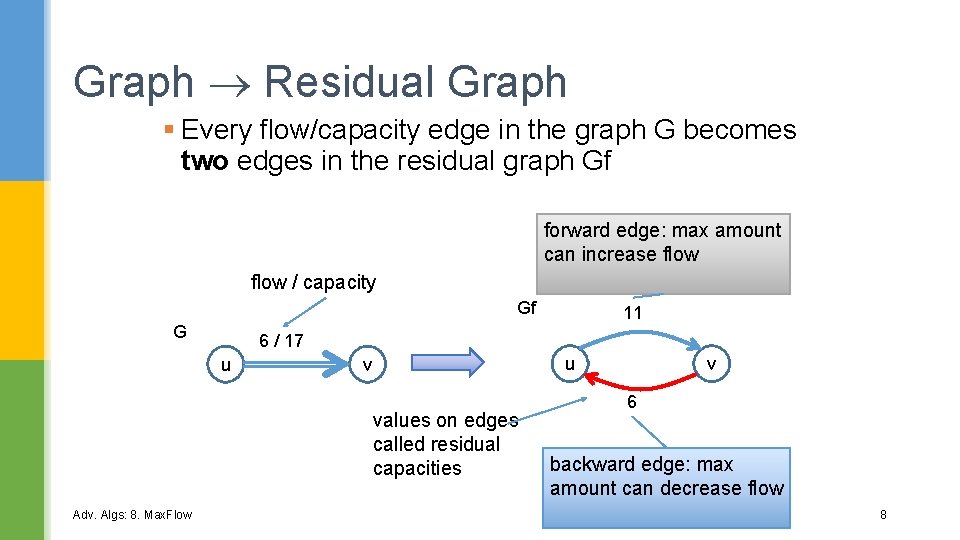
Graph Residual Graph § Every flow/capacity edge in the graph G becomes two edges in the residual graph Gf forward edge: max amount can increase flow / capacity Gf G 6 / 17 u u v values on edges called residual capacities Adv. Algs: 8. Max. Flow 11 v 6 backward edge: max amount can decrease flow 8

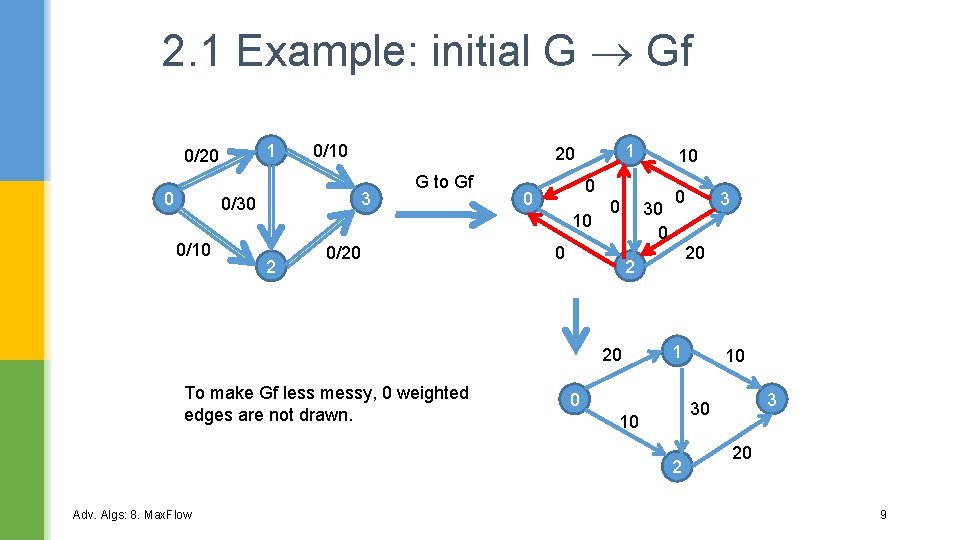
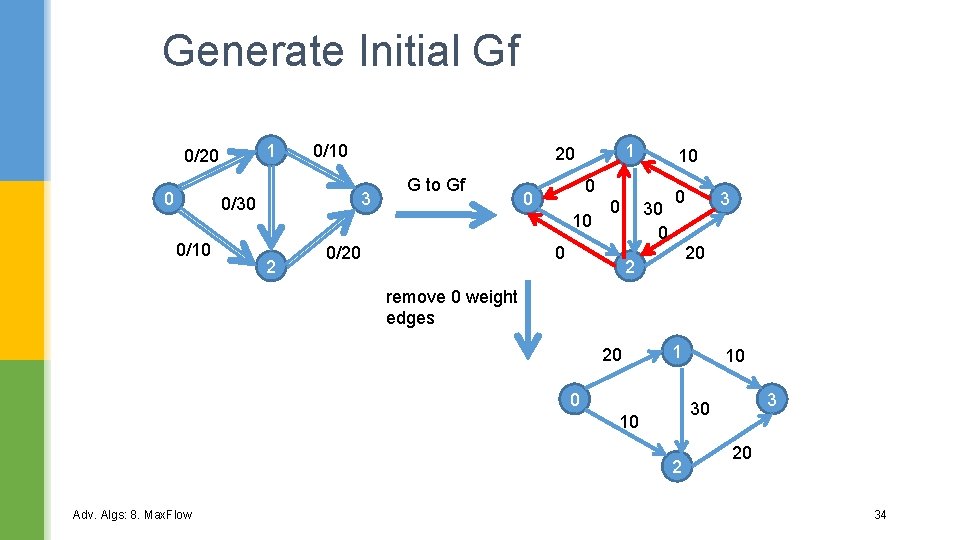
2. 1 Example: initial G Gf 1 0/20 0 1 20 3 0/30 0/10 G to Gf 0 0 10 2 0/20 0 0 30 0 0 10 3 30 10 2 Adv. Algs: 8. Max. Flow 3 20 2 20 To make Gf less messy, 0 weighted edges are not drawn. 10 20 9

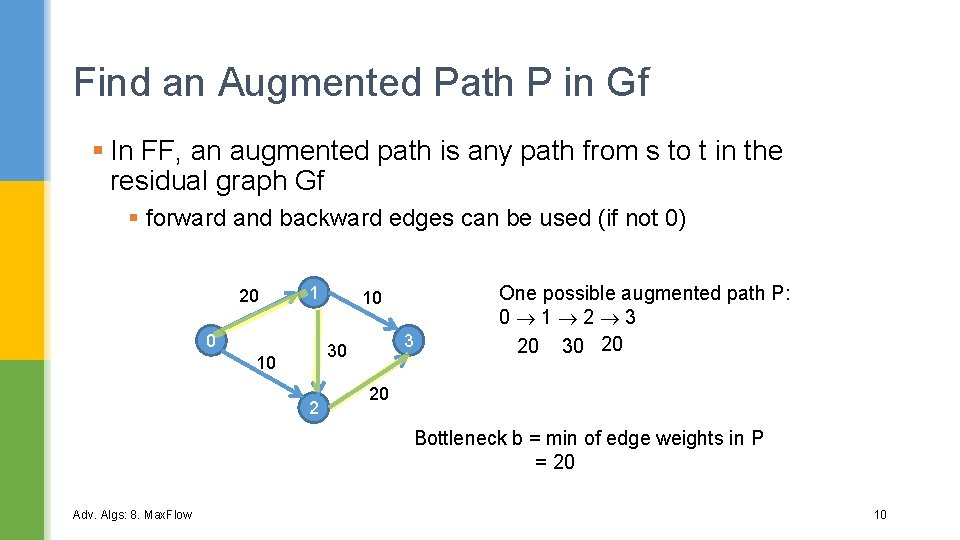
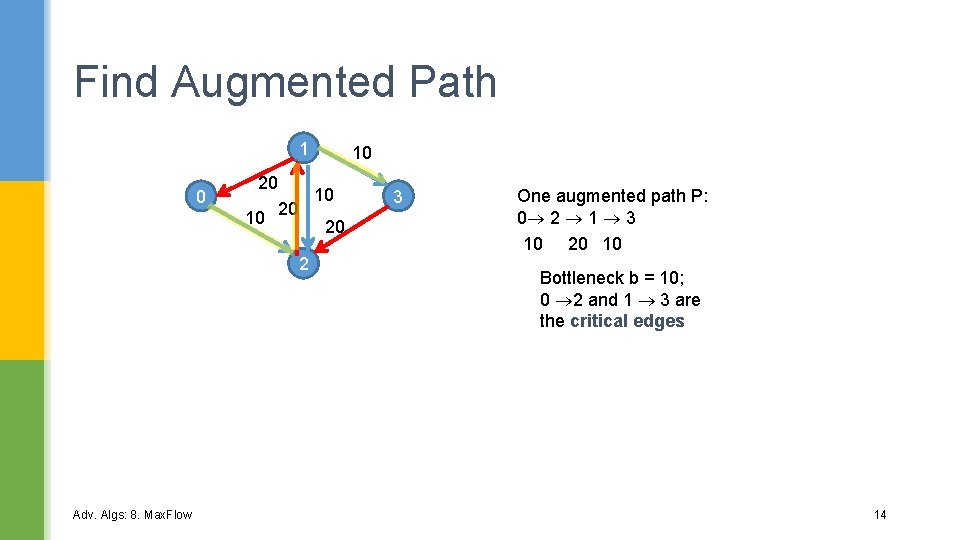
Find an Augmented Path P in Gf § In FF, an augmented path is any path from s to t in the residual graph Gf § forward and backward edges can be used (if not 0) 20 1 0 10 3 30 10 2 One possible augmented path P: 0 1 2 3 20 30 20 20 Bottleneck b = min of edge weights in P = 20 Adv. Algs: 8. Max. Flow 10

Augment Flow along P in G using b § The flow fe on each edge e in G can change in two ways: § fe = fe + b in G if the edge in P is a forward edge § i. e. increase the flow § fe = fe – b in G if the edge in P is a backward edge § i. e. decrease the flow Adv. Algs: 8. Max. Flow 11

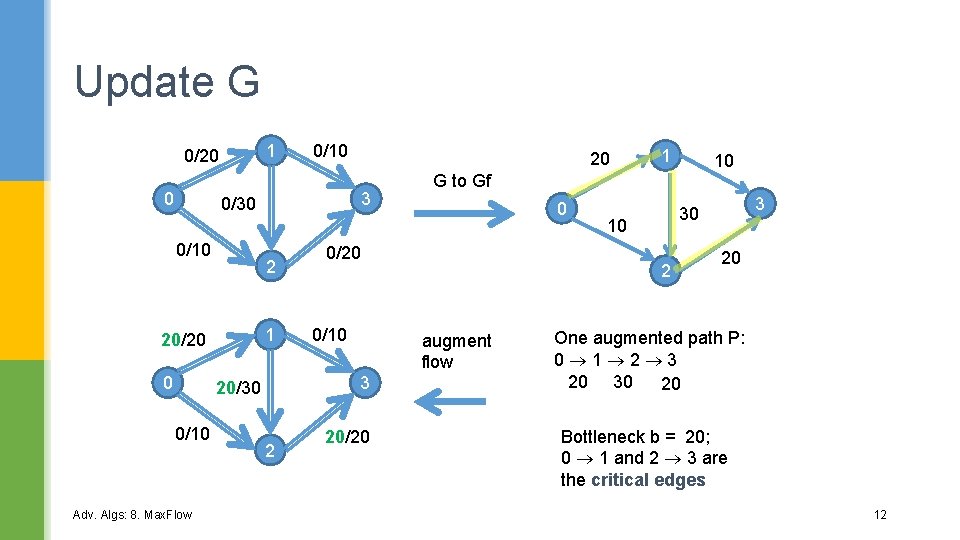
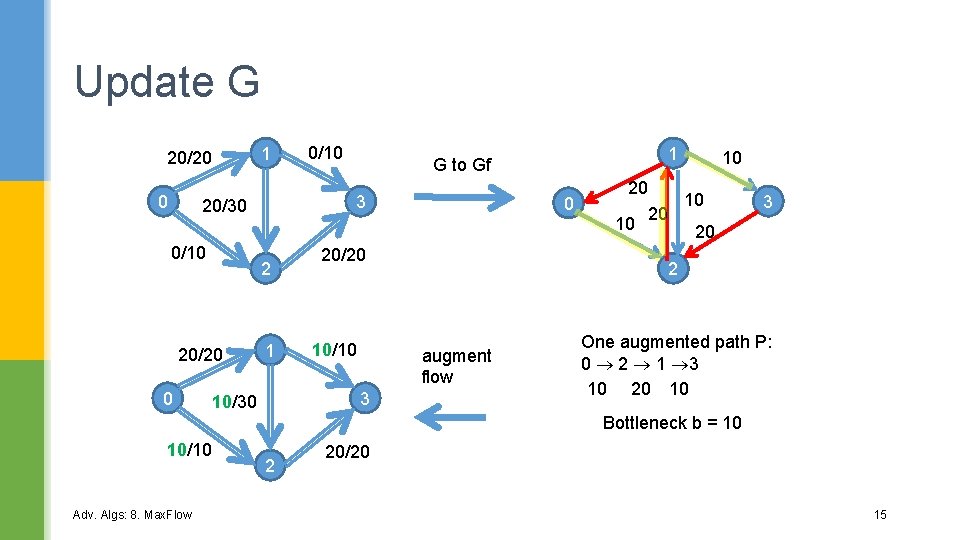
Update G 1 0/20 0 0/10 3 0/30 0/10 2 1 20/20 0 Adv. Algs: 8. Max. Flow 0/10 2 0 10 3 30 10 2 augment flow 20/20 1 G to Gf 0/20 3 20/30 0/10 20 20 One augmented path P: 0 1 2 3 20 30 20 Bottleneck b = 20; 0 1 and 2 3 are the critical edges 12

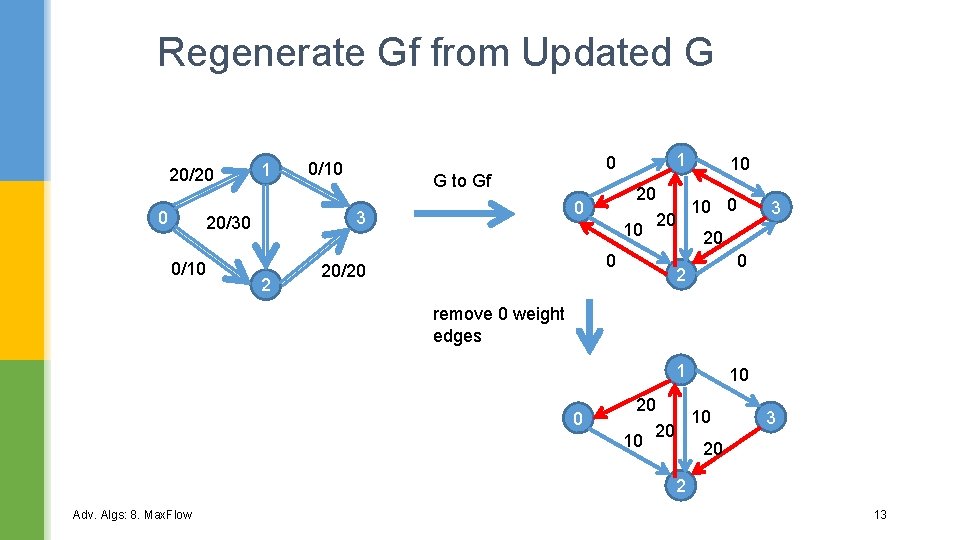
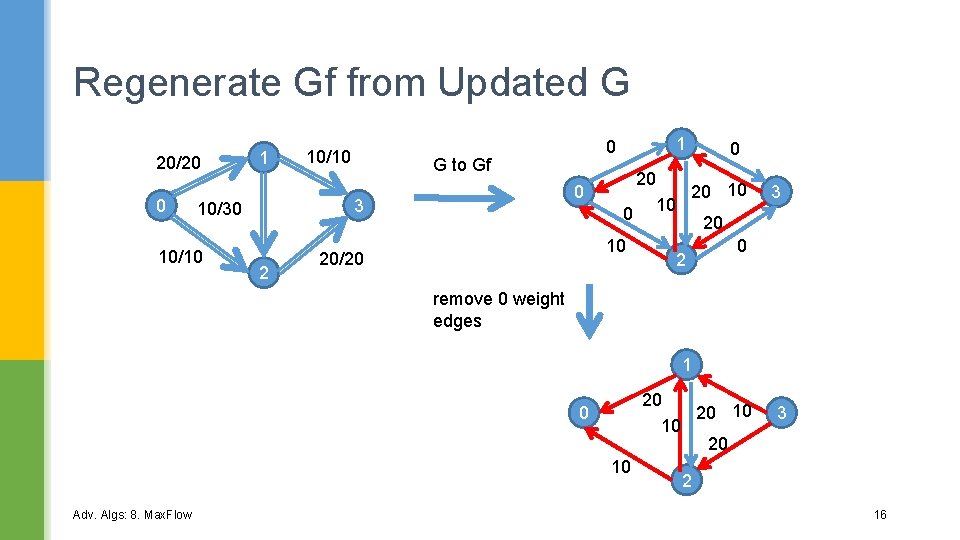
Regenerate Gf from Updated G 20/20 0 1 2 0 G to Gf 0 3 20/30 0/10 20/20 1 10 20 0 0 2 3 remove 0 weight edges 1 0 20 10 3 2 Adv. Algs: 8. Max. Flow 13

Find Augmented Path 1 0 20 10 20 2 Adv. Algs: 8. Max. Flow 10 3 One augmented path P: 0 2 1 3 10 20 10 Bottleneck b = 10; 0 2 and 1 3 are the critical edges 14

Update G 20/20 0 1 2 20/20 0 1 0 20/20 10/10 10 20 3 2 augment flow 3 10/30 1 G to Gf 3 20/30 0/10 One augmented path P: 0 2 1 3 10 20 10 Bottleneck b = 10 10/10 Adv. Algs: 8. Max. Flow 2 20/20 15

Regenerate Gf from Updated G 20/20 0 1 2 0 G to Gf 0 3 10/30 10/10 20/20 1 0 20 20 10 10 0 2 3 remove 0 weight edges 1 20 20 10 10 20 0 10 Adv. Algs: 8. Max. Flow 3 2 16

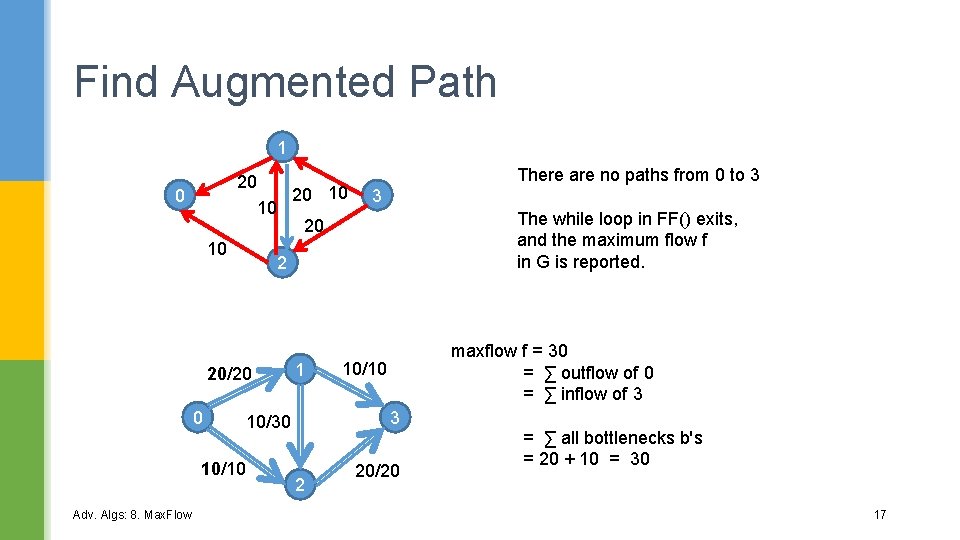
Find Augmented Path 1 20 20 10 10 20 0 10 1 The while loop in FF() exits, and the maximum flow f in G is reported. maxflow f = 30 = ∑ outflow of 0 = ∑ inflow of 3 10/10 3 10/30 10/10 Adv. Algs: 8. Max. Flow 3 2 20/20 0 There are no paths from 0 to 3 2 20/20 = ∑ all bottlenecks b's = 20 + 10 = 30 17

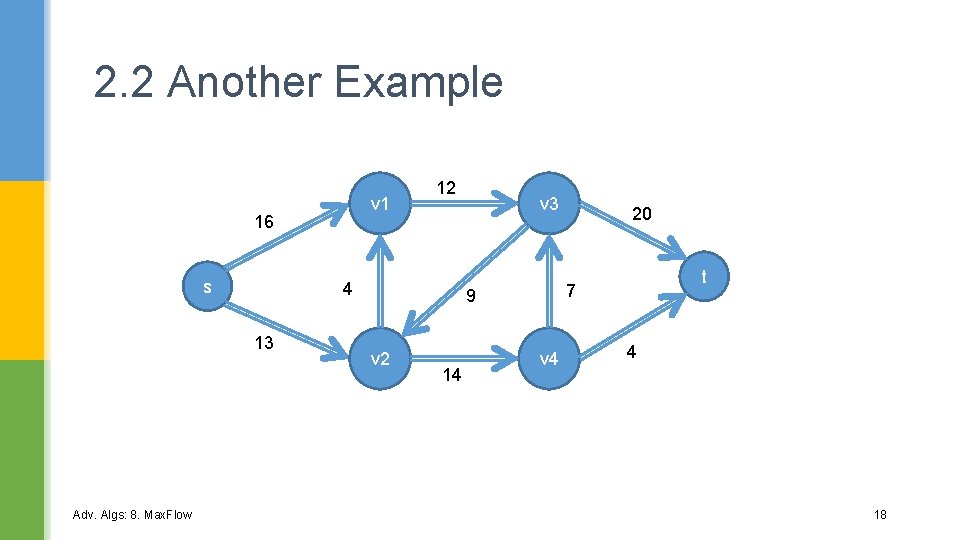
2. 2 Another Example v 1 16 s 4 13 Adv. Algs: 8. Max. Flow 12 v 3 14 t 7 9 v 2 20 v 4 4 18

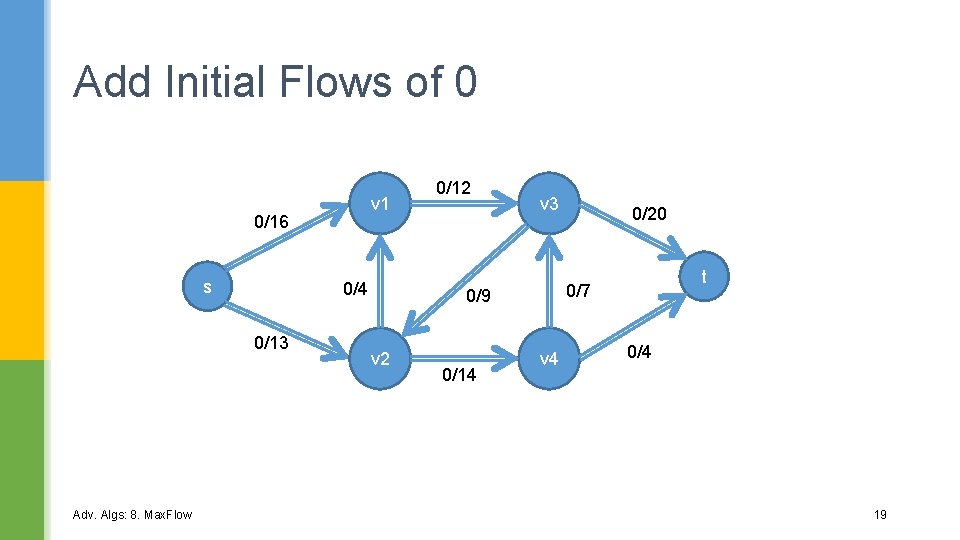
Add Initial Flows of 0 v 1 0/16 s 0/4 0/13 Adv. Algs: 8. Max. Flow 0/12 v 3 0/14 t 0/7 0/9 v 2 0/20 v 4 0/4 19

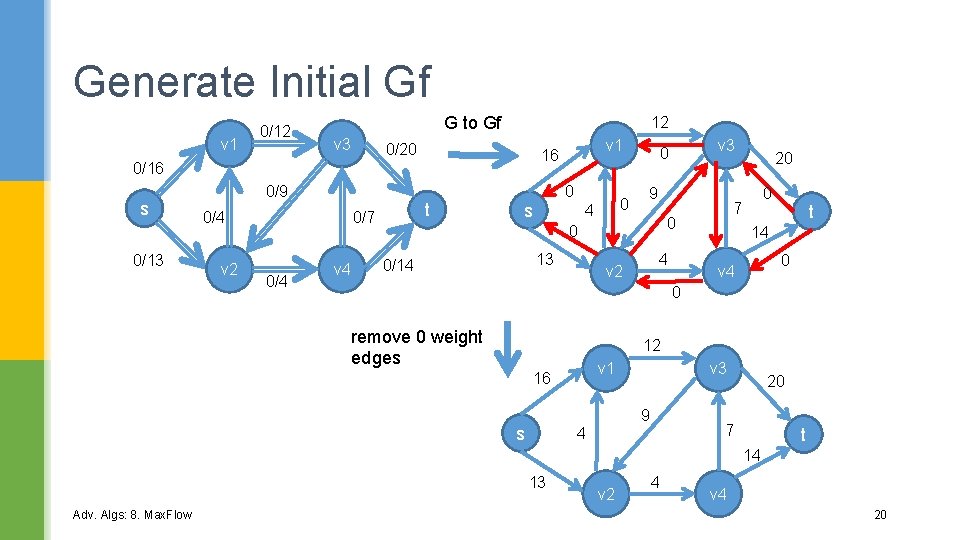
Generate Initial Gf v 1 0/12 G to Gf v 3 12 0/20 0/16 s 0/13 0/9 0/4 v 2 t 0/7 0/4 v 1 16 0 s 0 4 9 13 4 v 2 20 0 7 0 0 0/14 v 3 0 t 14 0 v 4 0 remove 0 weight edges 12 v 1 16 v 3 9 s 20 7 4 t 14 13 Adv. Algs: 8. Max. Flow v 2 4 v 4 20

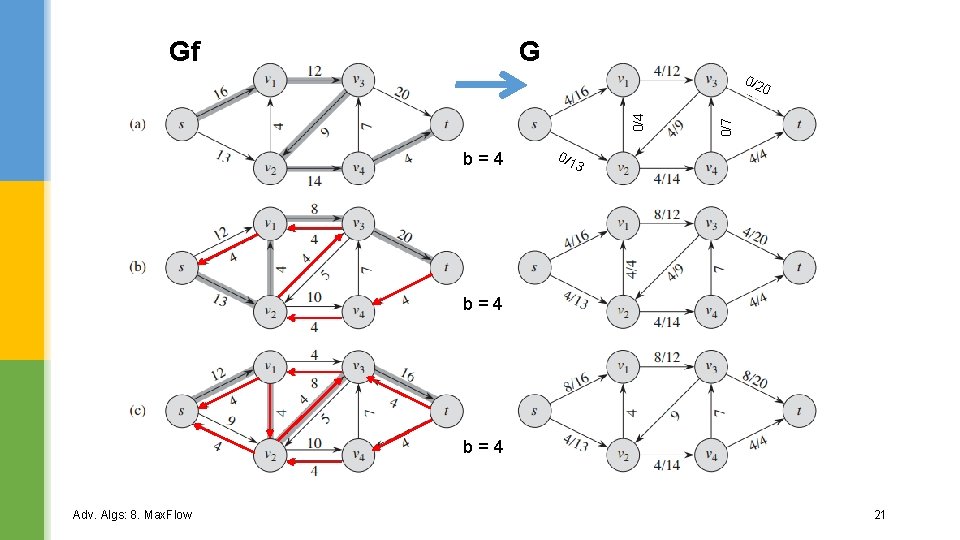
Gf G b=4 0 0/7 0/4 0/2 0/1 3 b=4 Adv. Algs: 8. Max. Flow 21

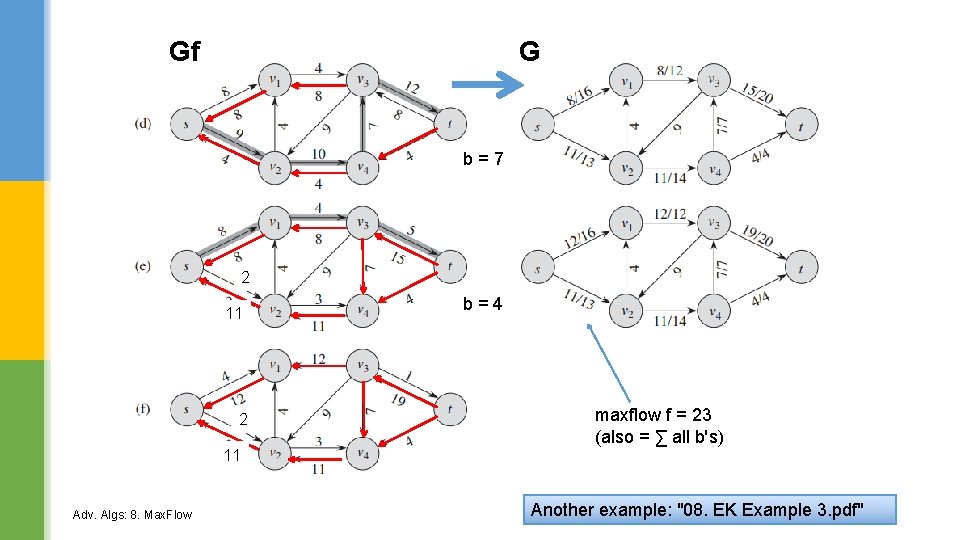
Gf G b=7 2 11 Adv. Algs: 8. Max. Flow b=4 maxflow f = 23 (also = ∑ all b's) Another example: "08. EK Example 3. pdf" 22

2. 3. FF Running Time dfs/bfs = O(V+E) = O(E) § void FF(Graph G, Node s, Node t) { initialize flows on all edges in G to 0; change G into residual graph Gf; O(E) maxflow f = 0; while (can find an augmented path P in Gf) { bottleneck b = minimum of edge weights in P; augment flow along P in G using b; O(E) f = f + b; regenerate Gf from updated G; O(E) } } report maxflow f in G; no. of loops = | f | Total Running time: O(E ∙ |f|)

Why no. of loops == |f|? § The loop stops when no more b's can be found. § The maxflow f = ∑ all b's § In the worst case each time round loop produces the smallest b, which is 1 § So it will take f loops before ∑ all b's == f § So max no. of loops == |f|

§ In the worst case, the running time of FF is O(E · |f|) § |f| might be very big depending on the problem. § It might be much larger than the number of edges.

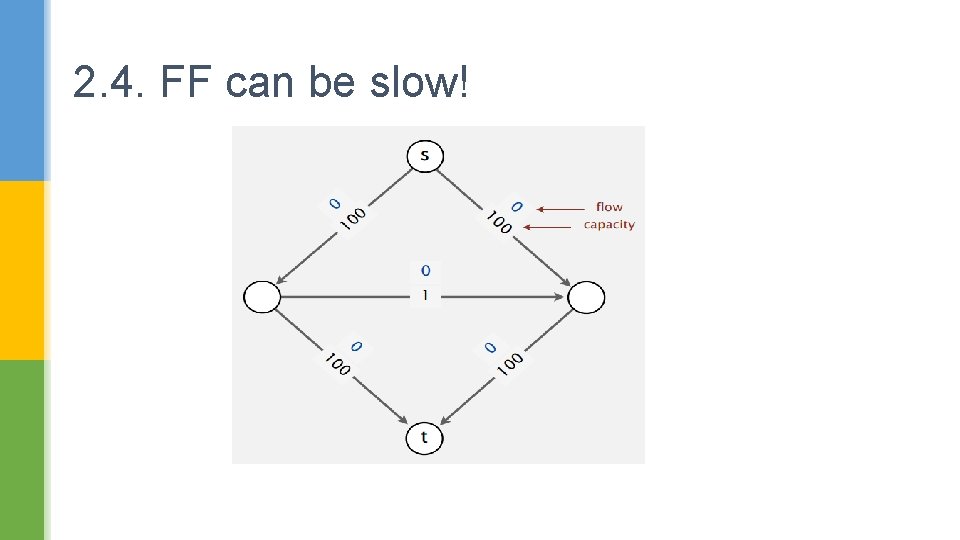
2. 4. FF can be slow!

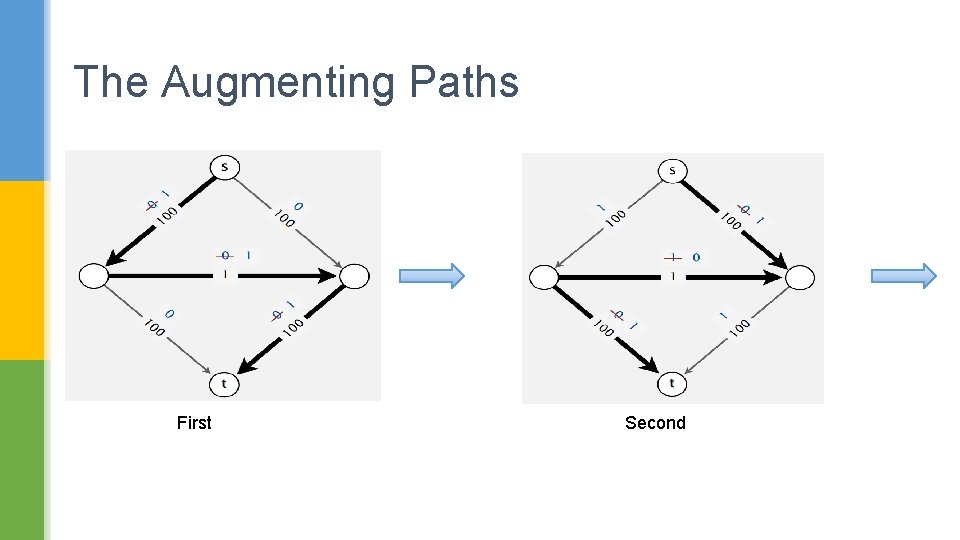
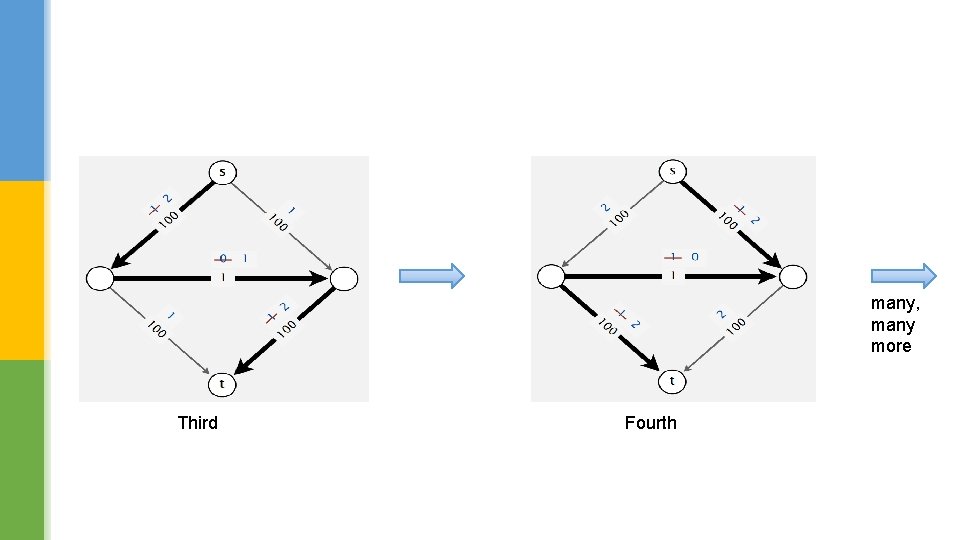
The Augmenting Paths First Second

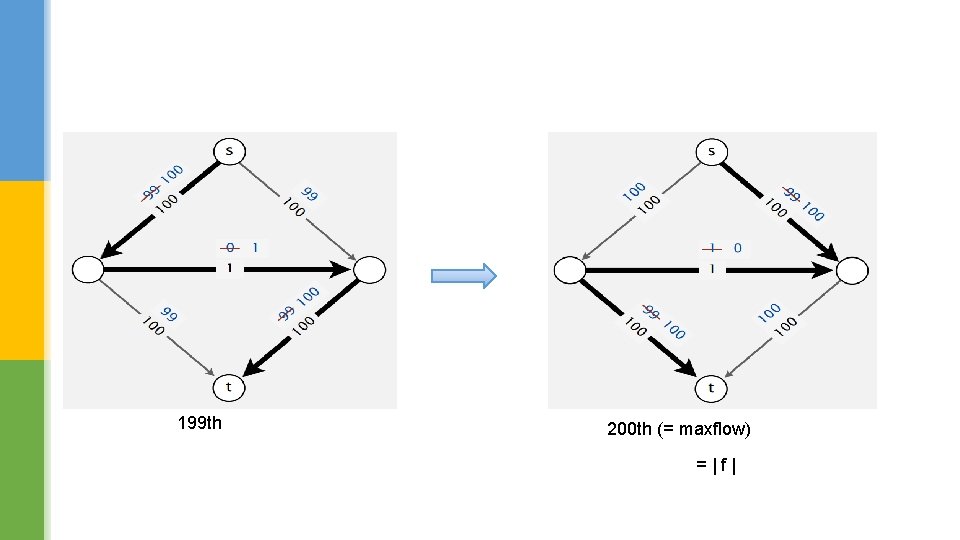
many, many more Third Fourth

199 th 200 th (= maxflow) =|f|

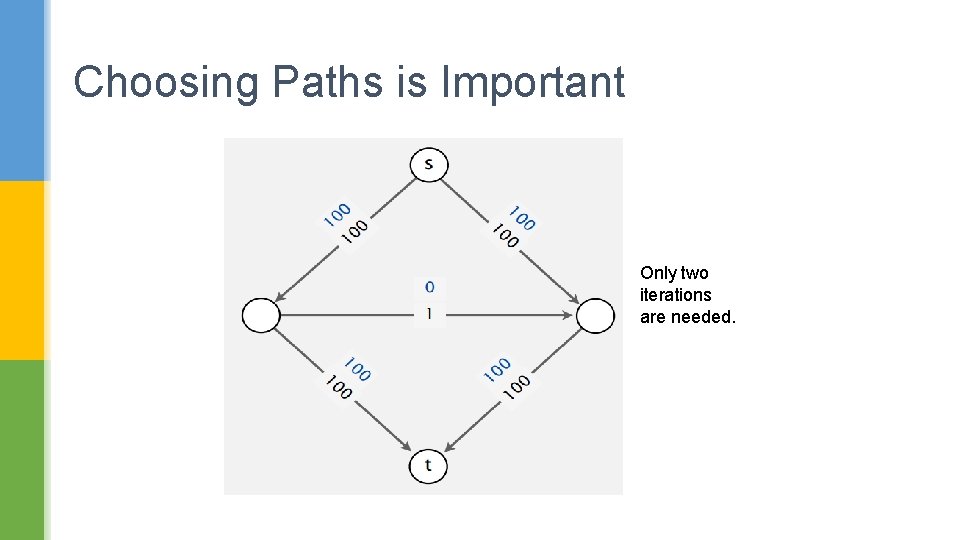
Choosing Paths is Important Only two iterations are needed.

3. Edmonds-Karp (EK) Algorithm void EK(Graph G, Node s, Node t) { change G into residual graph Gf; } bfs = O(V+E) = O(E) maxflow = 0; while (can find an augmented SHORTEST path P in Gf) { bottleneck b = minimum of edge weights in P; augment flow along P in Gf using b; maxflow += bottleneck; } print maxflow; Running time: O(V· E 2) no. of loops = O(V · E) Adv. Algs: 8. Max. Flow Smaller since V*E < |f| 31

§ It's not necessary to keep regenerating Gf from G. All the flow changes are applied to Gf directly. § Finds an augmenting path using breadth-first search § bfs implemented using a queue and a loop Adv. Algs: 8. Max. Flow 32

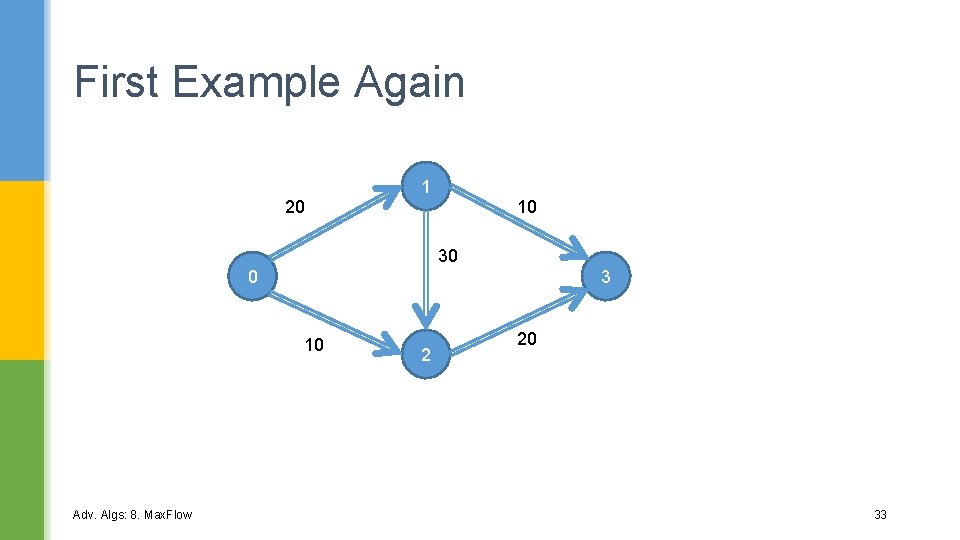
First Example Again 1 10 20 30 0 3 10 Adv. Algs: 8. Max. Flow 2 20 33

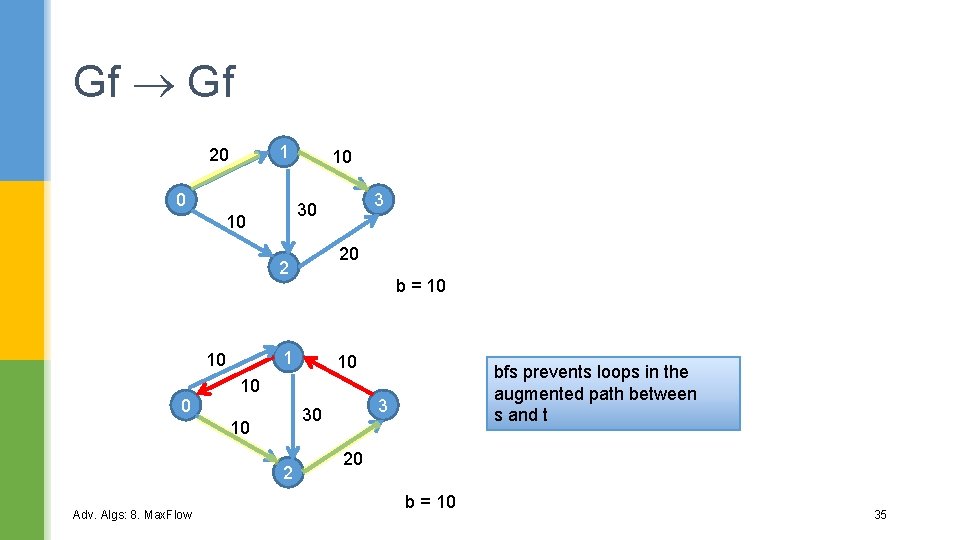
Generate Initial Gf 1 0/20 0 1 20 3 0/30 0/10 G to Gf 0 0 10 2 0/20 10 0 0 3 20 2 remove 0 weight edges 20 1 0 3 30 10 2 Adv. Algs: 8. Max. Flow 10 20 34

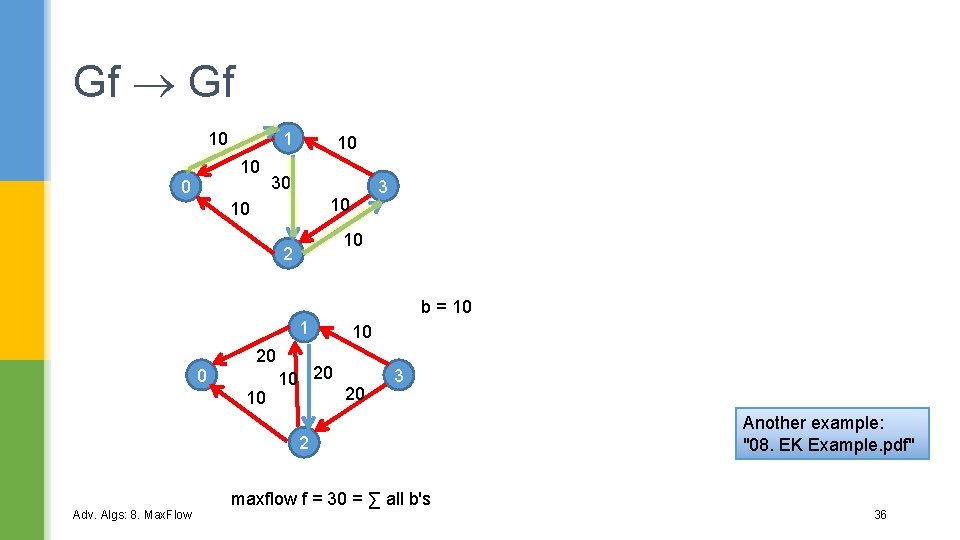
Gf Gf 1 20 0 10 10 20 2 0 10 10 2 bfs prevents loops in the augmented path between s and t 3 30 10 Adv. Algs: 8. Max. Flow b = 10 1 10 3 30 20 b = 10 35

Gf Gf 10 1 10 0 10 30 3 10 10 10 2 b = 10 1 0 20 10 10 20 3 2 Adv. Algs: 8. Max. Flow maxflow f = 30 = ∑ all b's Another example: "08. EK Example. pdf" 36

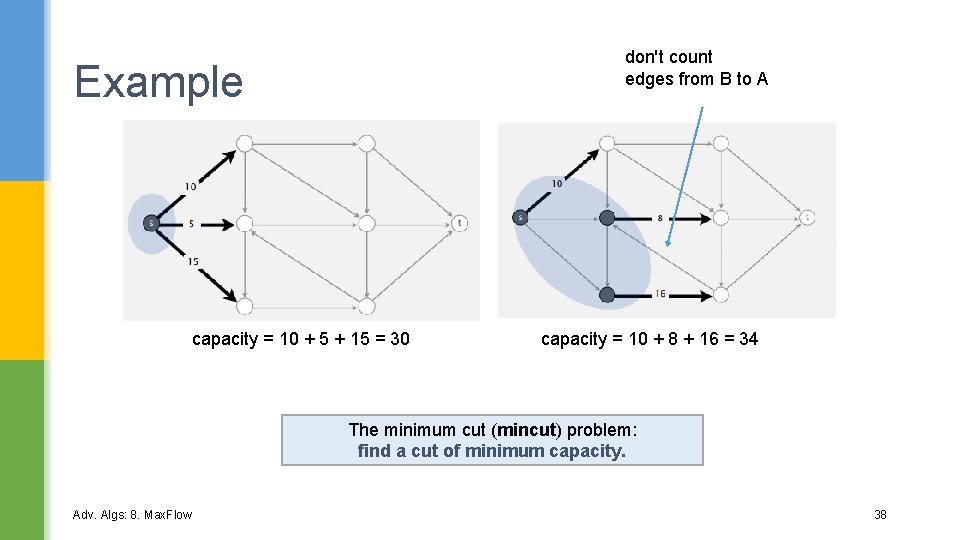
4. The Mincut Problem § A cut is a partition of a flow network's vertices into two disjoint sets, with the source (s) in one set A and the sink (t) in the other set B. § A cut's capacity is the sum of the capacities of the edges from A to B. § The minimum cut (mincut) problem: find a cut of minimum capacity. Adv. Algs: 8. Max. Flow 37

don't count edges from B to A Example capacity = 10 + 5 + 15 = 30 capacity = 10 + 8 + 16 = 34 The minimum cut (mincut) problem: find a cut of minimum capacity. Adv. Algs: 8. Max. Flow 38

Maxflow == Mincut § The maxflow problem § find a flow of maximum value § The mincut problem § find a cut of minimum capacity § Two problems that appear very different but are actually two versions of the same question. § Maxflow-mincut theorem: maxflow value = mincut capacity Adv. Algs: 8. Max. Flow 39

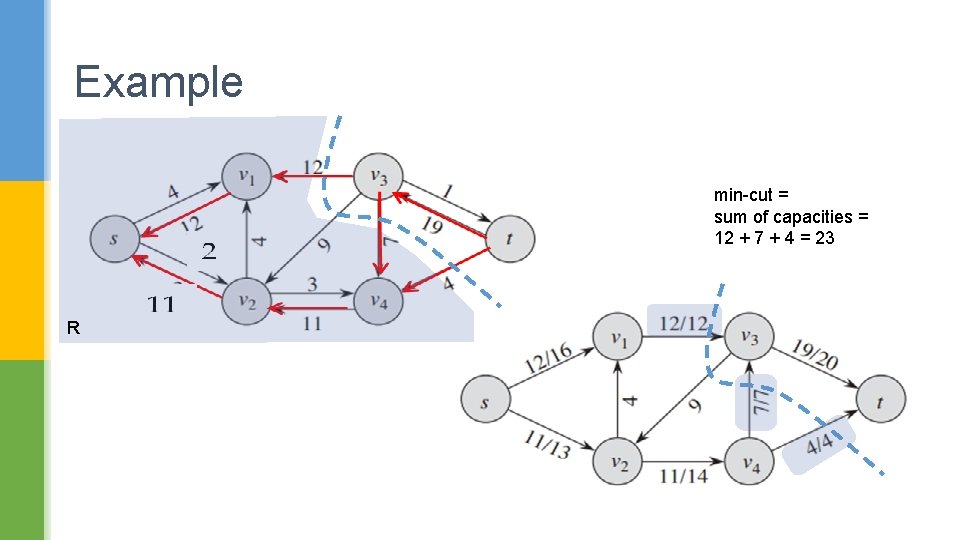
Finding the mincut § After the maxflow is found, the mincut is obtained in three steps. § 1. Collect all the vertices reachable from S in the Gf graph into subgraph R. § 2. The mincut divides the R subgraph from the rest of G. § 3. The mincut is the sum of the capacities leaving R.

Example min-cut = sum of capacities = 12 + 7 + 4 = 23 R

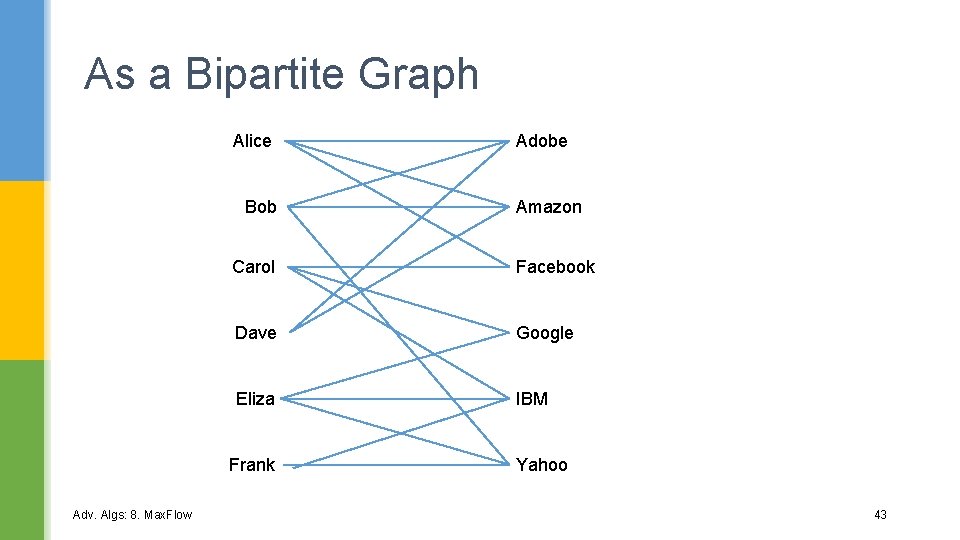
Offers: 5. Bipartite Matching § Students apply for jobs. § Each student gets several offers. § Is there a way to match every student to a different job? Adv. Algs: 8. Max. Flow 42

As a Bipartite Graph Alice Bob Amazon Carol Facebook Dave Google Eliza IBM Frank Adv. Algs: 8. Max. Flow Adobe Yahoo 43

Maximize No. of 1 -1 Edges Alice Bob Amazon Carol Facebook Dave Google Eliza IBM Frank Adv. Algs: 8. Max. Flow Adobe A perfect match Yahoo 44

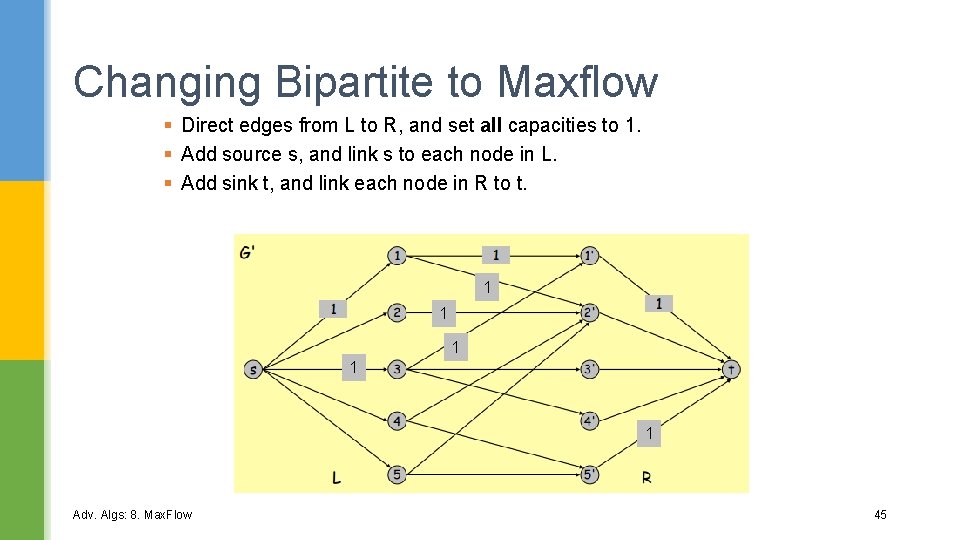
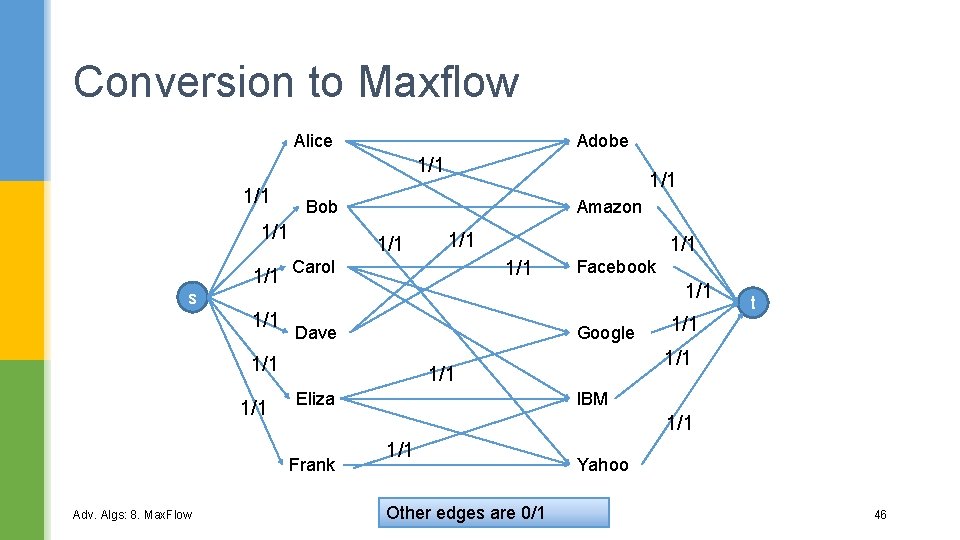
Changing Bipartite to Maxflow § Direct edges from L to R, and set all capacities to 1. § Add source s, and link s to each node in L. § Add sink t, and link each node in R to t. 1 1 1 Adv. Algs: 8. Max. Flow 45

Conversion to Maxflow Adobe Alice 1/1 1/1 Amazon Bob 1/1 1/1 Carol 1/1 Facebook 1/1 s 1/1 Google Dave 1/1 1/1 IBM Eliza 1/1 Frank Adv. Algs: 8. Max. Flow 1/1 t 1/1 Other edges are 0/1 Yahoo 46

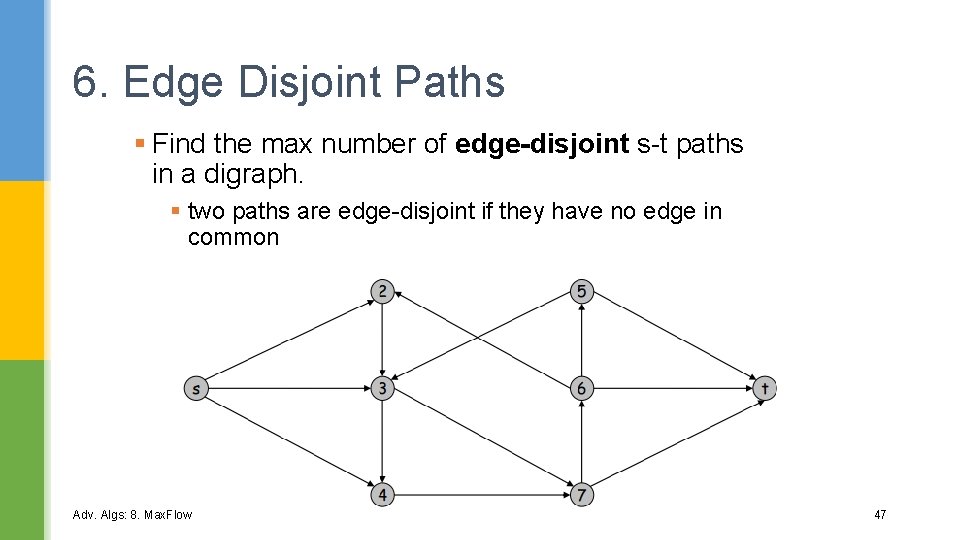
6. Edge Disjoint Paths § Find the max number of edge-disjoint s-t paths in a digraph. § two paths are edge-disjoint if they have no edge in common Adv. Algs: 8. Max. Flow 47

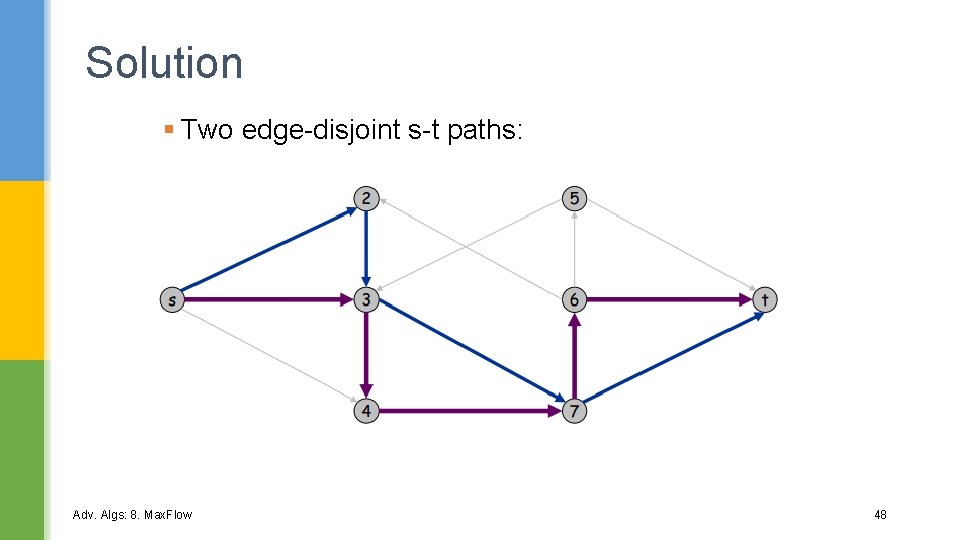
Solution § Two edge-disjoint s-t paths: Adv. Algs: 8. Max. Flow 48

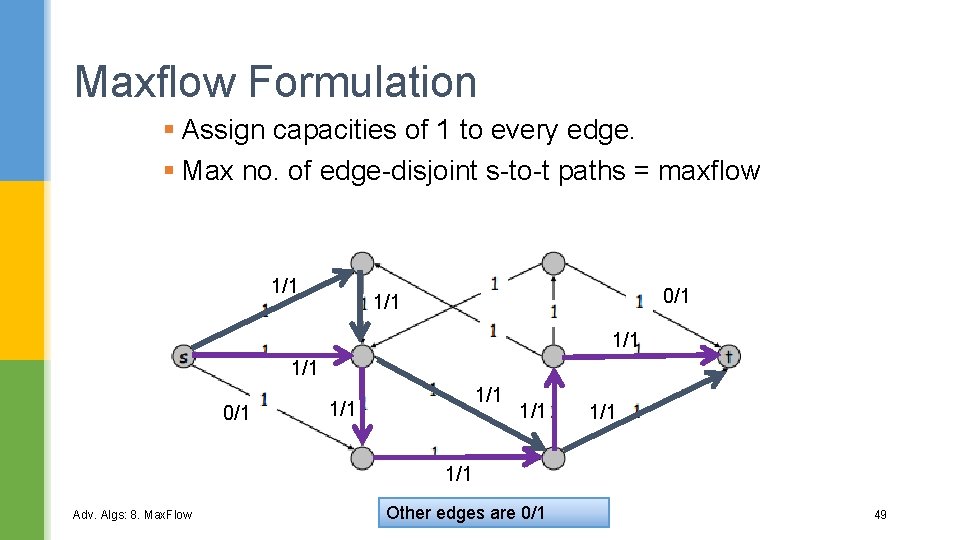
Maxflow Formulation § Assign capacities of 1 to every edge. § Max no. of edge-disjoint s-to-t paths = maxflow 1/1 0/1 1/1 1/1 Adv. Algs: 8. Max. Flow Other edges are 0/1 49

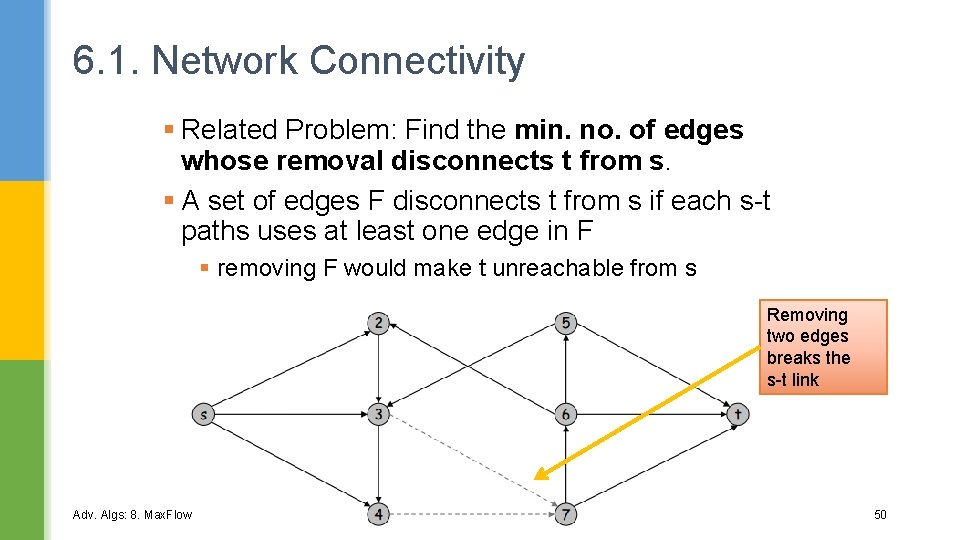
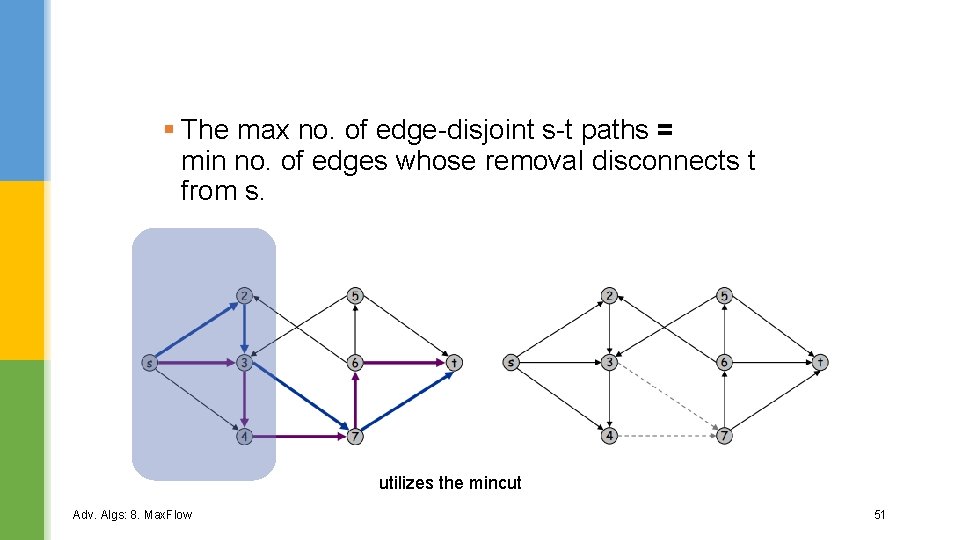
6. 1. Network Connectivity § Related Problem: Find the min. no. of edges whose removal disconnects t from s. § A set of edges F disconnects t from s if each s-t paths uses at least one edge in F § removing F would make t unreachable from s Removing two edges breaks the s-t link Adv. Algs: 8. Max. Flow 50

§ The max no. of edge-disjoint s-t paths = min no. of edges whose removal disconnects t from s. utilizes the mincut Adv. Algs: 8. Max. Flow 51

7. Making Max. Flow Faster year method worst case running time discovered by 1955 augmenting path O(E · |f|) Ford-Fulkerson 1970 shortest augmented path O(V · E 2) Edmonds-Karp 1983 dynamic trees O(E 2 · log E) Sleator-Tarjan 1985 capacity scaling O(E 2 · log C) Gabow 1997 length function O(E 3/2 · log E · log C) Goldberg-Rao ? ? E ? C is the biggest capacity on an edge in the graph.

Analysis is Tricky § Worst-case big-Oh is generally not useful for predicting or comparing real-world maxflow algorithm speeds. § Best in practice: push-relabel method with gap relabeling: O(E 3/2) (can be written as O(V 3) § very close to linear in E