Advanced Algorithms Analysis and Design By Dr Nazir

Advanced Algorithms Analysis and Design By Dr. Nazir Ahmad Zafar Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Lecture No 2 Mathematical Tools for Design and Analysis of Algorithms (Fundamentals of Algorithms) Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Review of Lecture No 1 • • Introduction to Algorithms Designing Techniques Algorithm is a Technology Model of Computation Even we have supercomputers, it requires algorithm Algorithms makes difference in users and modeler Some of the applications areas of algorithms Management and manipulation of data Electronic commerce Manufacturing and other commercial settings Shortest paths etc. Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Today Covered A Sequence of Mathematical Tools • Sets • Sequences • Order pairs • Cross Product • Relation • Functions • Operators over above structures • Conclusion Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Set • A set is well defined collection of objects, which are • unordered • distinct • same type • with common properties Notation: • Elements of set are listed between a pair of curly braces S 1 = {R, R, R, B, G} = {B, G, R} Empty Set S 3 = { } = , has not elements, called empty set Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Representation of Sets • Three ways to represent a set • Descriptive Form • Tabular form • Set Builder Form (Set Comprehension) Example • Descriptive Form S = set of all prime numbers • Tabular form {2, 3, 5, . . . } • Set Builder Form {x : N| ( i {2, 3, . . . , x-1} (i / x)) x} Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Set Comprehension Some More Examples {x : s | p x} = {x : s | p} = all x in s that satisfy p 1. 2. 3. 4. 5. 6. {x : Z | x 2 = x x} = {0, 1} {x : N | x 0 mod 2 x} = {0, 2, 4, . . . } {x : N | x 1 mod 2 x} = {1, 3, 5, . . . } {x : Z | x ≥ 0 x ≤ 6 x} = {0, 1, 2, 3, 4, 5, 6} {x : Z | x ≥ 0 x ≤ 6 x 2} = {0, 1, 4, . . . , 25, 36} {x : N | x 1 mod 2 x 3} = {1, 27, 125, . . . } Dr. Nazir A. Zafar Formal Methods

All collections are not sets • The prime numbers Primes == {2, 3, 5, 7, . . . } • The four oceans of the world Oceans == {Atlantic, Arctic, Indian, Pacific} • The passwords that may be generated using eight lowercase letters, when repetition is allowed • Hard working students in MSCS class session 2007 -09 at Virtual University • Intelligent students in your class • Kind teachers at VU Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Operators Over Sets Membership Operator • If an element e is a member of set S then it is denoted as e S and read e is in S. Let S is sub-collection of X X = a set S X Now : X x P X Bool (x, S) = = 1 0 Dr Nazir A. Zafar if x is in S if x is not in S Advanced Algorithms Analysis and Design

Operators Over Sets Subset: If each element of A is also in B, then A is said to be a subset of B, A B and B is superset of A, B A. Let X = a universal set, A X, B X, Now : X x X Bool (A, B) = = 1, if x : X, x A x B 0 if x : X, x A x B Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Operators Over Sets Intersection : X x X X (A, B) = = {x : X | x A and x B x} Union : X x X X (A, B) = = {x : X | x A or x B x} Set Difference : X x X X (A, B) = = {x : X | x A but x B x} Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Cardinality and Power Set of a given Set • A set, S, is finite if there is an integer n such that the elements of S can be placed in a one-to-one correspondence with {1, 2, 3, …, n}, and we say that cardinality is n. We write as: |S| = n Power Set • How many distinct subsets does a finite set on n elements have? There are 2 n subsets. • How many distinct subsets of cardinality k does a finite set of n elements have? There are Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Partitioning of a set A partition of a set A is a set of non-empty subsets of A such that every element x in A exactly belong to one of these subsets. Equivalently, set P of subsets of A, is a partition of A 1. If no element of P is empty 2. The union of the elements of P is equal to A. We say the elements of P cover A. 3. The intersection of any two elements of P is empty. That means the elements of P are pair wise disjoints Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Mathematical Way of Defining Partitioning A partition P of a set A is a collection {A 1, A 2, . . . , An} such that following are satisfied 1. Ai P, Ai , 2. Ai Aj = , i, j {1, 2, . . . , n} and i j 3. A = A 1 A 2 . . . An Example: Partitioning of Z Modulo 4 {x : Z | x 0 mod 4} = {. . . -8, -4, 0, 4, 8, . . . } = [0] {x : Z | x 1 mod 4} = {. . . -7, -3, 1, 5, 9, . . . } = [1] {x : Z | x 2 mod 4} = {. . . -6, -2, 2, 6, 10, . . . } = [ 2] {x : Z | x 3 mod 4} = {. . . -5, -1, 3, 7, 11, . . . } = [3] {x : Z | x 4 mod 4} = {. . . , -8, -4, 0, 4, 8, . . . } = [4] Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Sequence • It is sometimes necessary to record the order in which objects are arranged, e. g. , • Data may be indexed by an ordered collection of keys • Messages may be stored in order of arrival • Tasks may be performed in order of importance. • Names can be sorted in order of alphabets etc. Definition • A group of elements in a specified order is called a sequence. • A sequence can have repeated elements. Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Sequence • Notation: Sequence is defined by listing elements in order, enclosed in parentheses. e. g. S = (a, b, c), T = (b, c, a), U = (a, a, b, c) • Sequence is a set S = {(1, a), (2, b), (3, c)} = {(3, c), (2, b), (1, a)} • Permutation: If all elements of a finite sequence are distinct, that sequence is said to be a permutation of the finite set consisting of the same elements. • No. of Permutations: If a set has n elements, then there are n! distinct permutations over it. Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Operators over Sequences • Operators are for manipulations Concatenation • (a, b, c ) ( d, a ) = ( a, b, c, d, a ) Other operators • Extraction of information: ( a, b, c, d, a )(2) = b • Filter Operator: {a, d} ( a, b, c, d, a ) = (a, d, a) Note: • We can think how resulting theory of sequences falls within our existing theory of sets • And how operators in set theory can be used in case of sequences Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Tuples and Cross Product • A tuple is a finite sequence. • Ordered pair (x, y), triple (x, y, z), quintuple • A k-tuple is a tuple of k elements. Construction to ordered pairs • The cross product of two sets, say A and B, is A B = {(x, y) | x A, y B} | A B | = |A| |B| • Some times, A and B are of same set, e. g. , Z Z, where Z denotes set of Integers Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Binary Relations Definition: If X and Y are two non-empty sets, then X Y = {(x, y) | x X and y Y} Example: If X = {a, b}, Y = {0, 1} Then X Y = {(a, 0), (a, 1), (b, 0), (b, 1)} Definition: A subset of X Y is a relation over X Y Example: Compute all relations over X Y, where X = {a, b}, Y = {0, 1} R 1 = , R 2 = {(a, 0)}, R 3 = {(a, 1)} R 4 = {(b, 0)}, R 5 = {(b, 1)}, R 6 = {(a, 0), (b, 0)}, . . . There will be 24 = 16 number of relations Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Binary Relations Definition: X Y == (X Y) Example: If X = {a, b}, Y = {0, 1} Then X Y = {(a, 0), (a, 1), (b, 0), (b, 1)} and X Y = {R 1, R 2, R 3, R 4, R 5, R 6, R 7, R 8, R 9, R 10, R 11, R 12, R 13, R 14, R 15, R 16} Lemma 1: if #X = m, #Y = n then # (X Y) = 2 m n Algorithm: All binary relations, cardinality of it Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Equivalence Relation A relation R X X, is • Reflexive: (x, x) R, x X • Symmetric: (x, y) R (y, x) R, x, y X • Transitive: (x, y) R (y, z) R (x, z) R • Equivalence: If reflexive, symmetric and transitive Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

Applications : Order Pairs in Terms of String Definition • A relation R over X, Y, Z is some subset of X x Y x Z and so on Example 1 • If = {0, 1}, then construct set of all strings of length 2 and 3 • Set of length 2 = x = {0, 1} x {0, 1} = {(0, 0), (0, 1), (1, 0), (1, 1)} = {00, 01, 10, 11} • Set of length 3 = x x = {0, 1} x {0, 1} = {(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)} = {000, 010, 100, 110, 001, 011, 101, 111} Example 2 • If = {0, 1}, then construct set of all strings of length ≤ 3 • Construction = {} x x x Similarly we can construct collection of all sets of length n Dr Nazir A. Zafar Advanced Algorithms Analysis and Design

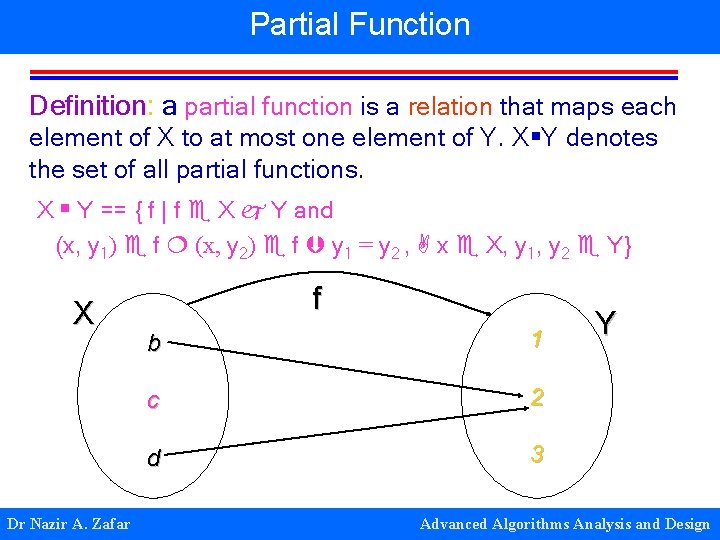
Partial Function Definition: a partial function is a relation that maps each element of X to at most one element of Y. X Y denotes the set of all partial functions. X Y == { f | f X Y and (x, y 1) f (x, y 2) f y 1 = y 2 , x X, y 1, y 2 Y} X Dr Nazir A. Zafar f b 1 c 2 d 3 Y Advanced Algorithms Analysis and Design

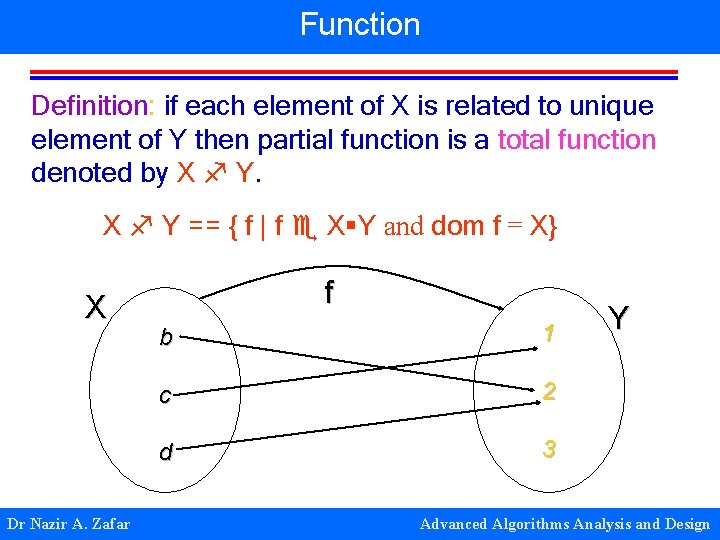
Function Definition: if each element of X is related to unique element of Y then partial function is a total function denoted by X Y == { f | f X Y and dom f = X} X Dr Nazir A. Zafar f b 1 c 2 d 3 Y Advanced Algorithms Analysis and Design

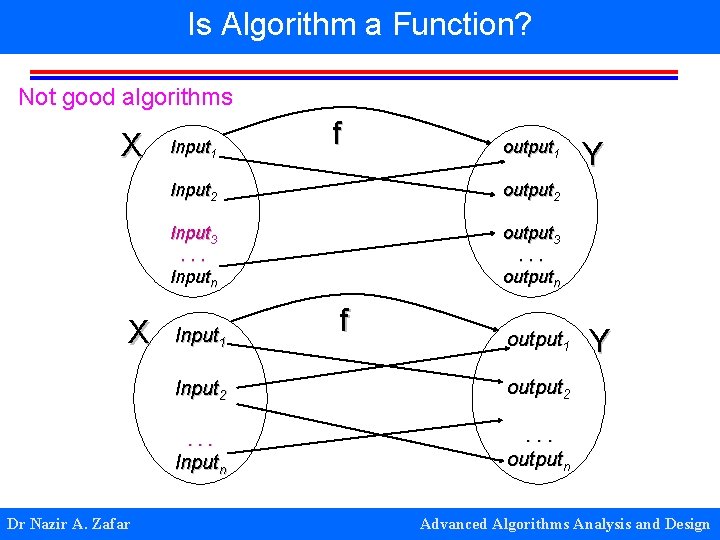
Is Algorithm a Function? Not good algorithms X X Input 1 output 1 Input 2 output 2 Input 3. . . Inputn output 3. . . outputn Input 1 f output 1 Input 2 output 2 . . . outputn Inputn Dr Nazir A. Zafar f Y Y Advanced Algorithms Analysis and Design

Conclusion • We started with sets and built other structures e. g. • Sequences • Relations • Functions, etc. • • We discussed operators over above structures All these tools are fundaments of mathematics Sets play key role in algorithms design and analysis Finally proving correctness of algorithms, we required logic. • Our next lecture will be on proving techniques Dr Nazir A. Zafar Advanced Algorithms Analysis and Design