Advanced Algebra with Trigonometry 4 1 Inverse Functions

Advanced Algebra with Trigonometry 4. 1 Inverse Functions

Inverse Concepts Stand Up Sit Down Go To Sleep Wake Up 2 Steps Forward, then turn Right Turn Left, then 2 Steps Backward Square, Mulitply, then Add Subtract, Divide, then Square Root

4. 1 Inverse Functions Inverse relation: a mapping of output values back to their original input values In plain English: switch the x and y!! (x, y) becomes (y, x)!! Write the inverse relation: {(2, 3), (5, 6), (9, 3)} Was the original relation a function? Yes {(3, 2), (6, 5), (3, 9) What about the inverse? No. . . 3 repeats If both the original relation and the inverse relation are functions, we call the two functions inverse functions. NOTE: f − 1 is read as f inverse. Two functions f and f − 1 are inverses of each other provided that f (f − 1(x)) = x and f − 1(f (x)) = x. Example] Let f(x) = x + 2. x→ f → f(x) → f− 1 5→ 5+2→ 7 f -1(x) = x – 2 → x 7→ 7– 2→ 5 x → f− 1 Let x = 5. → f− 1(x) → f →x 5→ 5– 2→ 3 3→ 3+2→ 5

Steps to find inverse: 1. Switch x and y 2. Solve for y Think of the inverse as “undoing” the original function. f(x) = 3 x + 1 (linear) Think: multiply by 3; then add 1 y = 3 x + 1 Write as y =; then switch x and y. x = 3 y + 1 Now, solve for y. 3 y + 1 = x This step just makes it easier on the eye. 3 y = x – 1 Think: subtract 1; then divide by 3. Rename y as f – 1(x)

Check both function compositions to insure we found the correct inverse!! f(x) = 3 x + 1 f(f – 1(x)) = f =3 =x– 1 + 1 =x (f – 1(f(x)) = f – 1(3 x + 1) = = =x +1

f(x) = x 2 + 2, x ≥ 0 y = x 2 + 2 x = y 2 + 2 (Note the domain restriction: we are only interested in the right side of the parabola. ) Switch x and y. y 2 + 2 = x Easier on the eye. y 2 = x − 2 Solve for y. y= f− 1(x) = Because the original domain was restricted to non-zero reals, you are only interested in the positive portion of the solution.

Check both function compositions to insure we found the correct inverse!! f(x) = x 2 + 2, x ≥ 0 f− 1(x) = f(f – 1(x)) = f = =x– 2+2 =x (f – 1(f(x)) = f – 1(x 2 + 2) = = =x

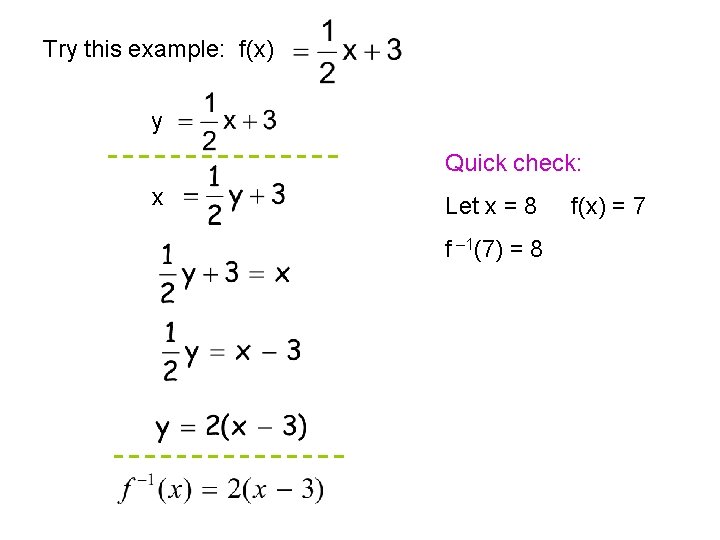
Try this example: f(x) y Quick check: x Let x = 8 f – 1(7) = 8 f(x) = 7

Try this example: f(x) = x 3 + 5 y = x 3 + 5 x = y 3 + 5 = x y 3 = x – 5 Quick check: f(2) = 13 f – 1 (13) = 2

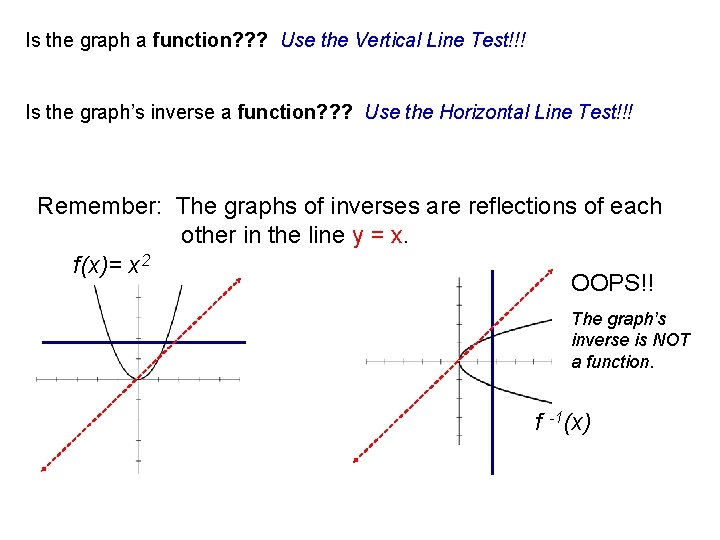
Is the graph a function? ? ? Use the Vertical Line Test!!! Is the graph’s inverse a function? ? ? Use the Horizontal Line Test!!! Remember: The graphs of inverses are reflections of each other in the line y = x. f(x)= x 2 OOPS!! The graph’s inverse is NOT a function. f -1(x)

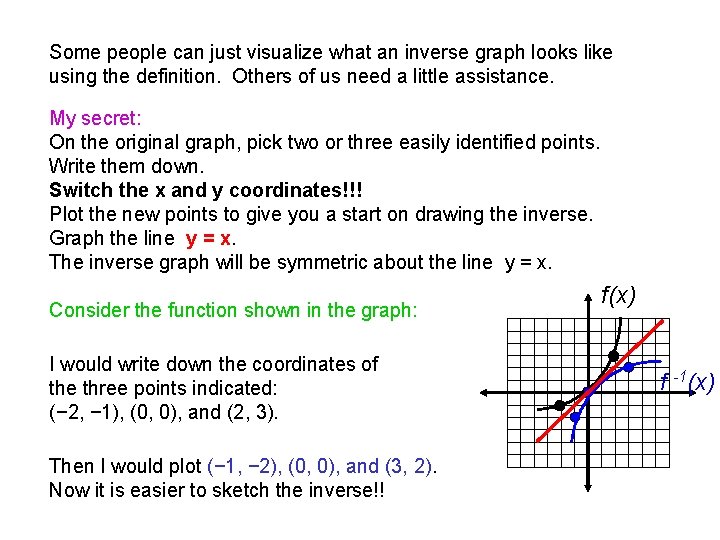
Some people can just visualize what an inverse graph looks like using the definition. Others of us need a little assistance. My secret: On the original graph, pick two or three easily identified points. Write them down. Switch the x and y coordinates!!! Plot the new points to give you a start on drawing the inverse. Graph the line y = x. The inverse graph will be symmetric about the line y = x. Consider the function shown in the graph: I would write down the coordinates of the three points indicated: (− 2, − 1), (0, 0), and (2, 3). Then I would plot (− 1, − 2), (0, 0), and (3, 2). Now it is easier to sketch the inverse!! f(x) f -1(x)

Review: To find the inverse of a relation or function: Switch x and y. Solve for y. To test if two relations are functions: Use Composition to verify that f(g(x)) equals x and g(f(x)) equals x Don’t forget about any domain restrictions!