Advance Data Structure Review of Chapter 2 Review

Advance Data Structure Review of Chapter 2 張啟中

Review of Chapter 2 Arrays n n 1. 3 Data Abstraction and Encapsulation 2. 2 The Array As An abstract Data Type q n 2. 5 The Representation of Arrays Example q q q 2. 3 The Polynomial Abstract Data Type 2. 4 The Sparse Matrix Abstract Data Type 2. 6 The String Abstract Data Type

定義：Data Type A data type is a collection of objects and a set of operations that act on those objects. 定義：Abstract Data Type An abstract data type(ADT) is a data type that is organized in such a way that the specification of the objects and the operations on the objects is separated from the representation of the objects and the implementation of the operations.

資料型態 n n n Data Types Primitive Data Types Accumulated Data Types - Array - Structures - Union Abstract Data Types Examples

Accumulated Data Type n Array n Struct n Union

The Array as an Abstract Data Type n Array q q A collection of data of the same type An array is usually implemented as a consecutive set of memory locations n n int list[5], *plist[5] ADT definition of an Array q q More general structure than "a consecutive set of memory locations. “ An array is a set of pairs, <index, value>, in mathematical, call correspondence or mapping

class General. Array { // objects: A set of pairs <index, value> where for each value of index in // Index. Set there is a value of type float. Index. Set is a finite ordered set of one // or more dimensions, for example, {0, …, n - 1} for one dimension, {(0, 0), // (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)} for two dimensions, etc. public: General. Array(int j, Range. List list, float init. Value = default. Value) ; // The constructor General. Array creates a j dimensional array of floats; the // range of the kth dimension is given by the kth element of list. For each // index i in the index set, insert <i, init. Value> into the array. float Retrieve(index i) ; // if (i is in the index set of the array) return the float associated with i in the // array; else signal an error. void Store(index i, float x) ; // if (i is in the index set of the array) delete any pair of the form <i, y> // present in the array and insert the new pair <i, x>; else signal an error. } ; // end of General. Array

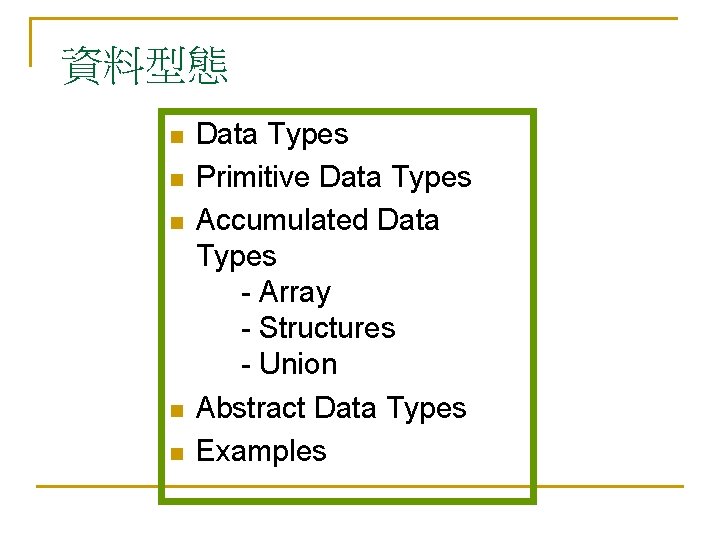
一維陣列和記憶體間的對應 Memory m m+2 m+4 m+6 int i. Array[100]; 7 51 22 43 9 0 98 99 1 2 假定 sizeof(int) = 2 m + 198

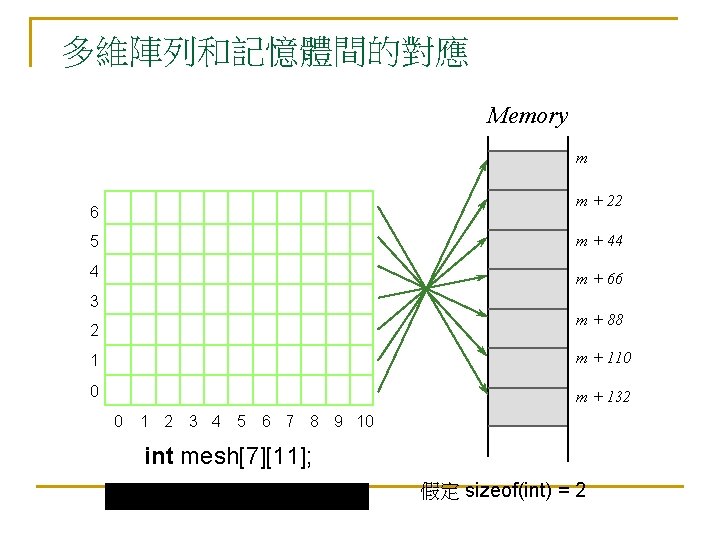
多維陣列和記憶體間的對應 Memory m m + 22 6 5 m + 44 4 m + 66 3 m + 88 2 1 m + 110 0 m + 132 0 1 2 3 4 5 6 7 8 9 10 int mesh[7][11]; 假定 sizeof(int) = 2

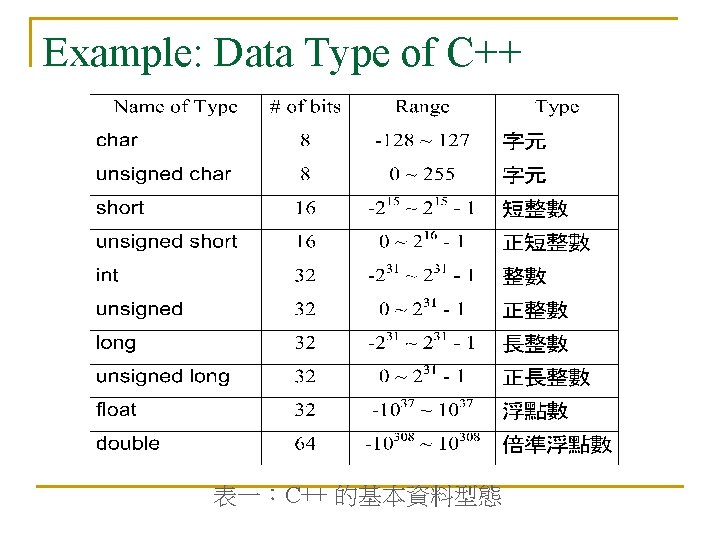
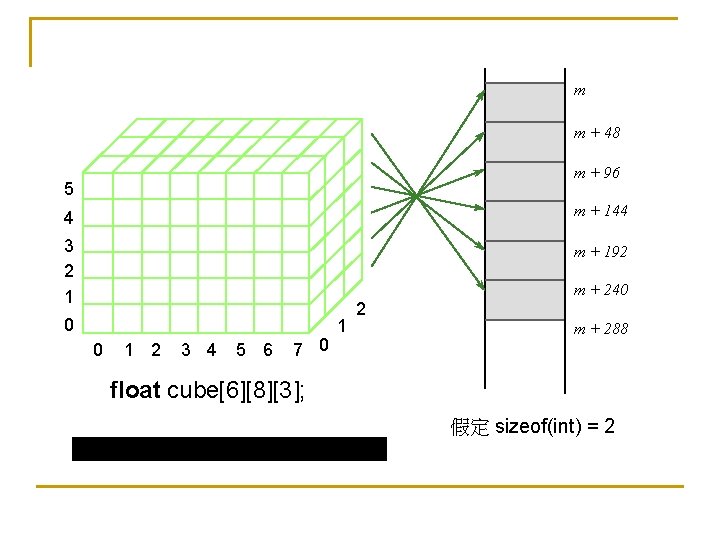
多維陣列的宣告 type array_name[array. Size 1]. . . [array. Sizen]; 【範例】 int mesh[7][11]; 6 5 4 3 2 1 0 float cube[6][8][3]; 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 1 0 2

m m + 48 m + 96 5 4 m + 144 3 2 1 m + 192 0 0 1 2 3 4 5 6 7 0 1 2 m + 240 m + 288 float cube[6][8][3]; 假定 sizeof(int) = 2

struct 和記憶體間的對應 m struct student. Type { char Name[20]; // 姓名 char Address[30]; // 地址 char Phone. Number[10]; // 電話 int Age; // 年齡 char Department[4]; // 系別 int Year; // 年級 char Class; // 班級 }; student. Type Student 1, Student 2; 假定 sizeof(int) = 2 m + 20 m + 50 m + 62 m + 66 m + 68

Self-Referential Structures One or more of its components is a pointer to itself. typedef struct list { char data; list *link; } Construct a list with three nodes item 1. link=&item 2; item 2. link=&item 3; malloc: obtain a node list item 1, item 2, item 3; item 1. data=‘a’; a b item 2. data=‘b’; item 3. data=‘c’; item 1. link=item 2. link=item 3. link=NULL; c

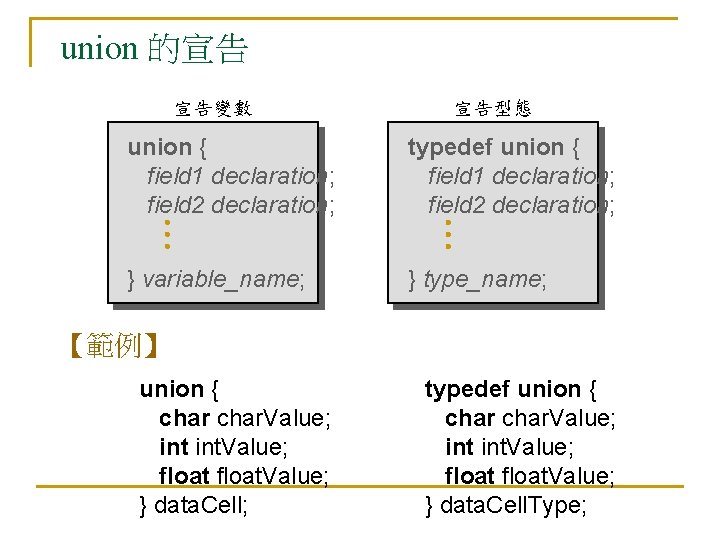
union 的宣告 宣告變數 宣告型態 union { field 1 declaration; field 2 declaration; typedef union { field 1 declaration; field 2 declaration; } variable_name; } type_name; 【範例】 union { char. Value; int. Value; float. Value; } data. Cell; typedef union { char. Value; int. Value; float. Value; } data. Cell. Type;

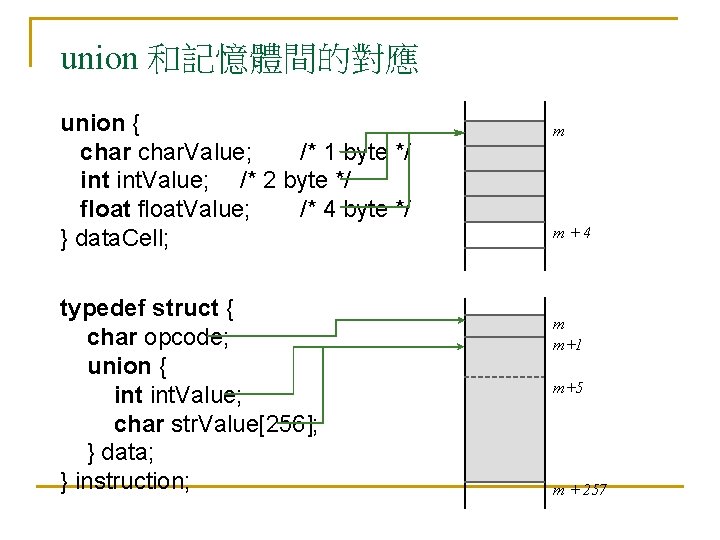
union 和記憶體間的對應 union { char. Value; /* 1 byte */ int. Value; /* 2 byte */ float. Value; /* 4 byte */ } data. Cell; typedef struct { char opcode; union { int. Value; char str. Value[256]; } data; } instruction; m m+4 m m+1 m+5 m + 257

Example n n Ordered List Polynomial ADT Sparse Matrix ADT String ADT

Ordered List Examples ordered (linear) list: (item 1, item 2, item 3, …, itemn) n (MONDAY, TUEDSAY, WEDNESDAY, THURSDAY, FRIDAY, SATURDAYY, SUNDAY) n (2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, ACE) n (1941, 1942, 1943, 1944, 1945) n (a 1, a 2, a 3, …, an-1, an) () n

Operations on Ordered List n n n Find the length, n , of the list. Read the items from left to right (or right to left). Retrieve the i’th element. Store a new value into the i’th position. Insert a new element at the position i , causing elements numbered i, i+1, …, n to become numbered i+1, i+2, …, n+1 Delete the element at position i , causing elements numbered i+1, …, n to become numbered i, i+1, …, n-1 array (sequential mapping)? (1)~(4) O (5)~(6) X

Polynomial（多項式） Addition: Multiplication:

class Polynomial { // objects: p(x) = a 0 xe 0 + … + anxen; a set of ordered pairs of <ei, ai>, where // ai ∈ Coefficient and ei ∈ Exponent // We assume that Exponent consists of integer ≥０ public: Polynomial() ; // return the polynomial p(x) = 0 int operator!() ; // if *this is the zero polynomial, return 1; else return 0; Coefficient Coef(Exponent e) ; // return the coefficient of e in *this Exponent Lead. Exp() ; // return the largest exponent in *this Polynomial Add(Polynomial poly) ; // return the sum of the polynomials *this and poly Polynomial Mult(Polynomial poly); // return the product of the polynomials *this and poly float Eval(float f) ; //Evaluate the polynomial *this at f and return the result. }; // end of Polynomial

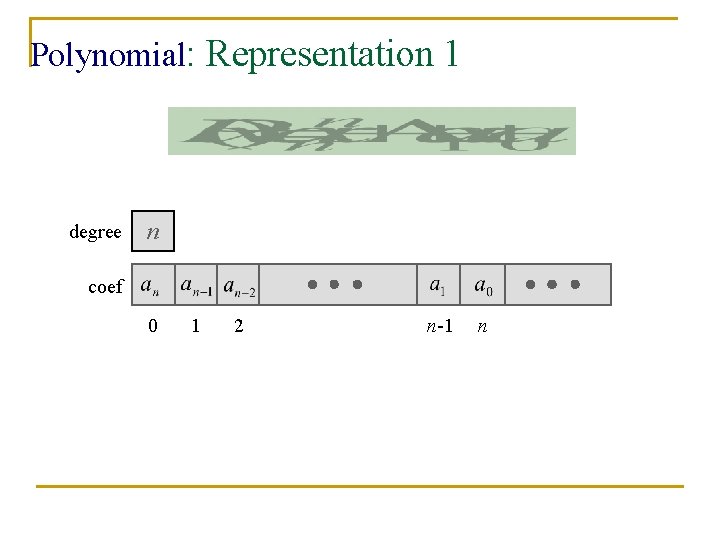
Polynomial: Representation 1 n Representation by Degrees private int degree; // degree Max. Degree float coef [Max. Degree + 1]; n Example: Let A(x)=Σaixi , then a. degree= n, a. coef[i]=an-i, , 0<= i<= n

Polynomial: Representation 1 degree n coef 0 1 2 n-1 n

Polynomial: Representation 2 n Representation by Degrees, but dynamic allocation space private: int degree; degree //degree <= Max. Degree float *coef; coef polynomial: : polynomial(int d) { degree= d, coef=new float[degree+1]; }

Polynomial: Representation 3 n Representation by Terms. Class polynomial; Class term { Friend polynomial; private: int exp float coef; coef }; n In polynomial class private: static term. Array[Max. Terms]; // Max. Terms is a constant. // term. Array[Max. Terms] shared by all polynomial objects. static int free; int start, finish; n In Implement file of polynomial class term Polynomial: : term. Array[Max. Terms]; int polynomial: : free = 0;

Polynomial: Representation 3 -1 A(X)=2 X 1000+1 B(X)=X 4+10 X 3+3 X 2+1 A. start A. finish B. start B. finish free coef exp 0 1 2 3 4 In general, A. Finish = A. Start + n – 1. For zero polynomial, A. Finish = A. Start – 1 5 6

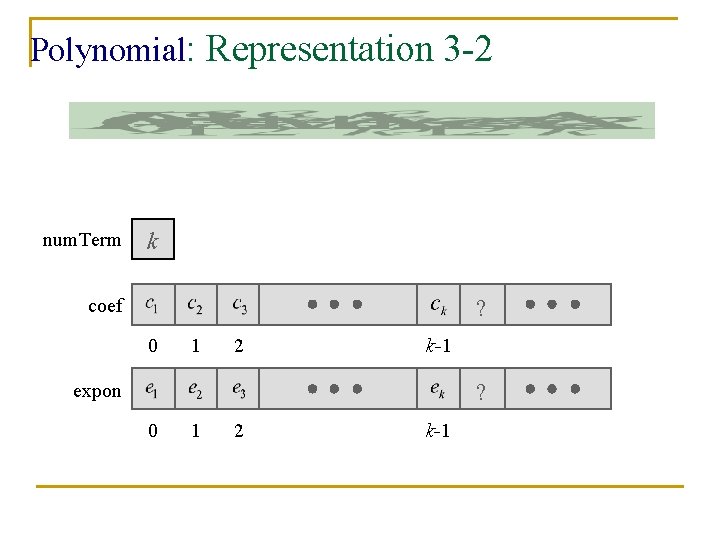
Polynomial: Representation 3 -2 num. Term k ? coef 0 1 2 k-1 ? expon 0 1 2 k-1

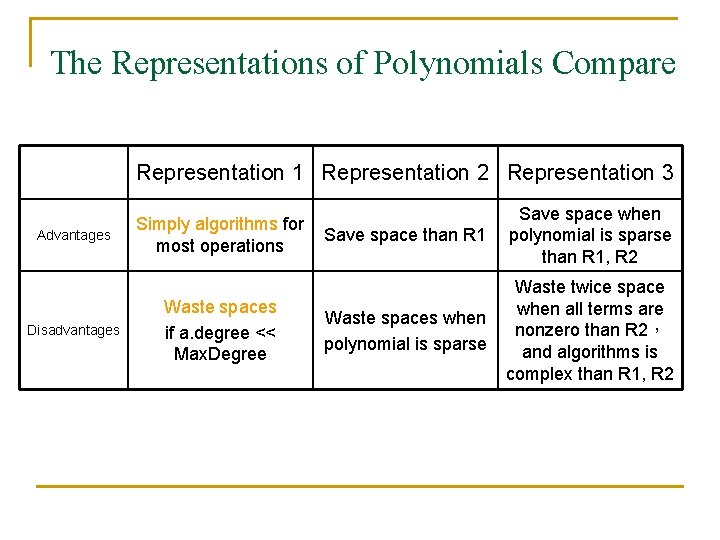
The Representations of Polynomials Compare Representation 1 Representation 2 Representation 3 Advantages Disadvantages Simply algorithms for most operations Waste spaces if a. degree << Max. Degree Save space than R 1 Save space when polynomial is sparse than R 1, R 2 Waste spaces when polynomial is sparse Waste twice space when all terms are nonzero than R 2， and algorithms is complex than R 1, R 2

操作分析 n 多項式相加 q n As Representation 3，we take O(m+n) at time complexity，if A(x) has m terms, B(x) has n terms. See Book pp. 83 -84 多項式相乘

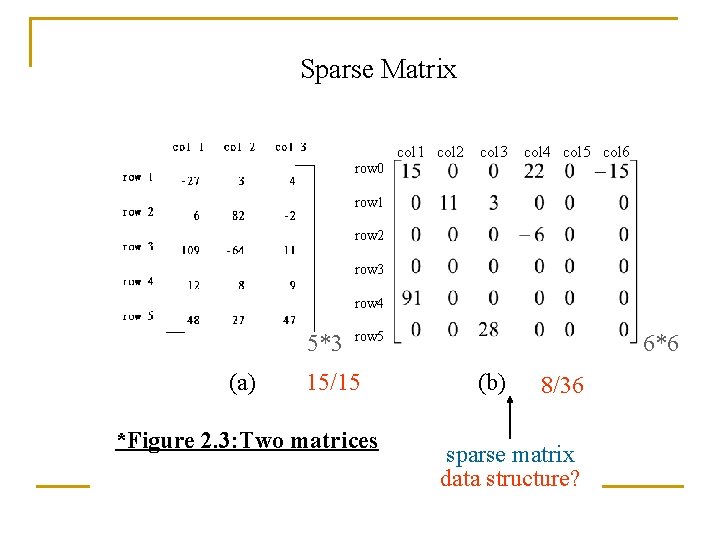
Sparse Matrix col 1 col 2 col 3 col 4 col 5 col 6 row 0 row 1 row 2 row 3 row 4 5*3 (a) row 5 15/15 *Figure 2. 3: Two matrices 6*6 (b) 8/36 sparse matrix data structure?

Abstract Data Type Sparse Matrix class Sparse. Matrix { //objects: a set of triples, <row, column, value>, where row and column are integers and // form a unique combination, and value comes from the set item. public: Sparse. Matrix(int Max. Row, int Max. Col); //create a Sparse. Matrix that can hold up to Max. Items= Max. Row*Max. Col and whose //maximum row size is Max. Row and whose maximum column size is Max. Col Sparse. Matrix Transpose(); Transpose // return the matrix produced by interchanging the row and column value of every triple. Sparse. Matrix Add(Sparse. Matrix b); Add //if the dimensions of a(*this) and b are the same, return the matrix produced by adding //corresponding items, namely those with identical row and column values. else return //error. Sparse. Matrix Multiply(a, Multiply b); //if number of columns in a equals number of rows in b return the matrix d produced by //multiplying a by b according to the formula: d[i][j]= Sum(a[i][k](b[k][j]), //where d(i, j) is the (i, j)th element, k=0 ~ ((columns of a) – 1) else return error. };

Representation of Sparse Matrix class Sparse. Matrix; class Matrix. Term { friend class Sparse. Matrix private: int col, row, value; }; n In class Sparse. Matrix private: int col, row, Terms; Matrix. Term sm. Array[Max. Terms]; // Note: triples are ordered by row and within rows by columns

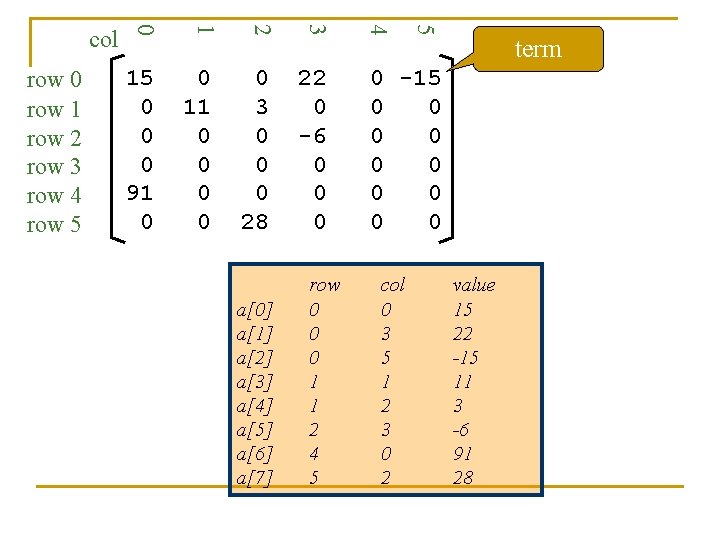
4 0 3 0 0 0 28 22 0 -6 0 0 -15 0 0 0 0 0 a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] row 0 0 0 1 1 2 4 5 col 0 3 5 1 2 3 0 2 5 3 0 11 0 0 2 15 0 0 0 91 0 1 row 0 row 1 row 2 row 3 row 4 row 5 0 col term value 15 22 -15 11 3 -6 91 28

Sparse Matrix 運算分析 n n n 轉置 (transpose) 相加 相乘

Abstract Data Type String Class String { //objects: a finite set of zero or more characters. public: String (char *init, int m); //Constructor that initializes *this to string init of length is m. int operator==(string t); // if the string represented by *this equal string t return 1(true) else return 0(false) int operator!(); // if *this is empty then return 1(TRUE); else return 0 (FALSE). int Length(); Length //return the number of characters in *this. String Concat(String t); Concat //return a string whose elements are those of *this followed by those of t. String Substr(int i, int j); Substr //return the string containing j characters of *this at positions i, i+1, . . . , i+j-1, //if these are valid positions of *this; else return empty string. int Find(String pat); //return an index i such that pat matches the substring of *this that begins at //position i. Return – 1 if pat is either empty or not a substring of *this. };

Pattern Matching n n Given two strings, string and pat, where pat is a pattern to be searched for in string Two methods q q a simple algorithm n O(S*P) O(n 2) optimal algorithm (by Knuth-Morris-Pratt) n n Linear complexity O(S+P) O(n)

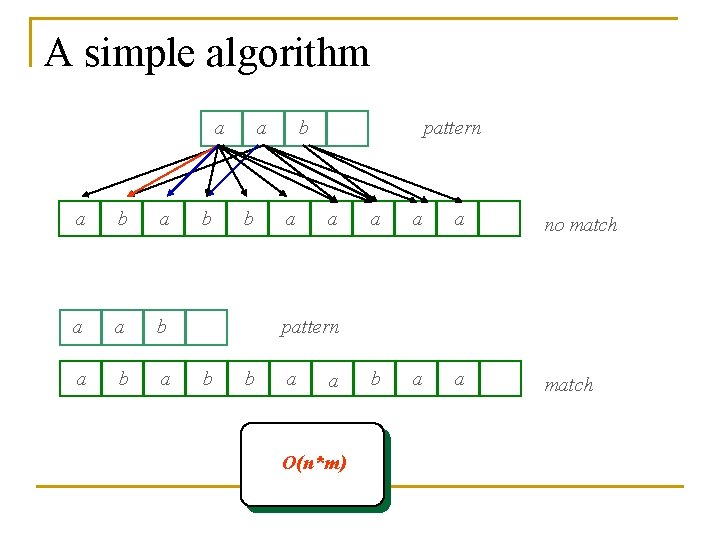
A simple algorithm a a b a b a b b a pattern a a no match b a a match pattern b b a a O(n*m)

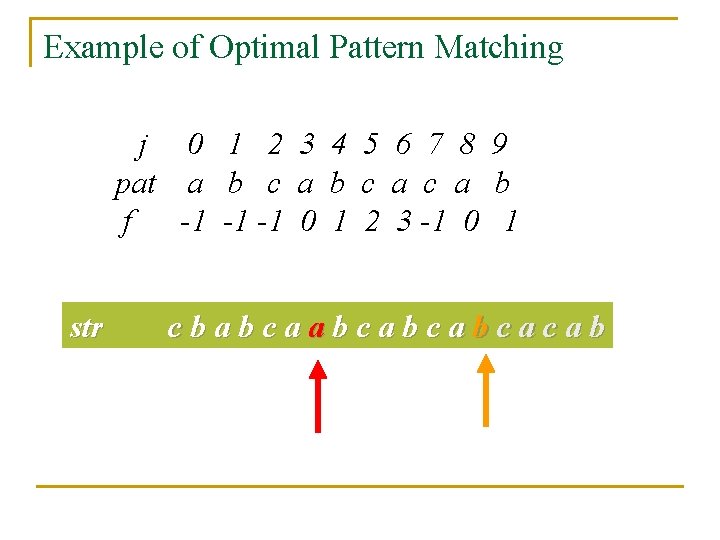
The Failure Function n Definition q n If p= p 0 p 1. . . pn-1 is a pattern, then its failure function, f is defined as: f(j) = largest i< j such that p 0 p 1. . . pi= pj-i+1. . . pj , i>= 0 = -1, otherwise Example j pat f 0 1 2 3 4 5 6 7 8 9 a b c a c a b -1 -1 -1 0 1 2 3 -1 0 1

Rule for Optimal Pattern Matching n If a partial match is found such that si-j. . . si-1= p 0 p 1. . . pj-1 and si<>pj then matching may be resumed by comparing si and pf(j-1)+1 if j<>0. If j= 0, continue by comparing si+1 and p 0 string a b c a ? ? . . . ? pat a b c a c a b f -1 -1 -1 0 1 2 3 -1 0 1 Continue here

Example of Optimal Pattern Matching j 0 1 2 3 4 5 6 7 8 9 pat a b c a c a b f -1 -1 -1 0 1 2 3 -1 0 1 str cbabcabcabcacab