ADT Table The ADT table is appropriate for

ADT Table • The ADT table is appropriate for problems that must manage data by value. • Some important operations of the ADT table are: – Inserting a data item containing the value x. – Delete a data item containing the value x. – Retrieve a data item containing the value x. • Various table implementations are possible for the ADT table. • We have to analyze the possible implementations so that we can make an intelligent choice. – Some operations are implemented more efficiently in certain implementations. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 1

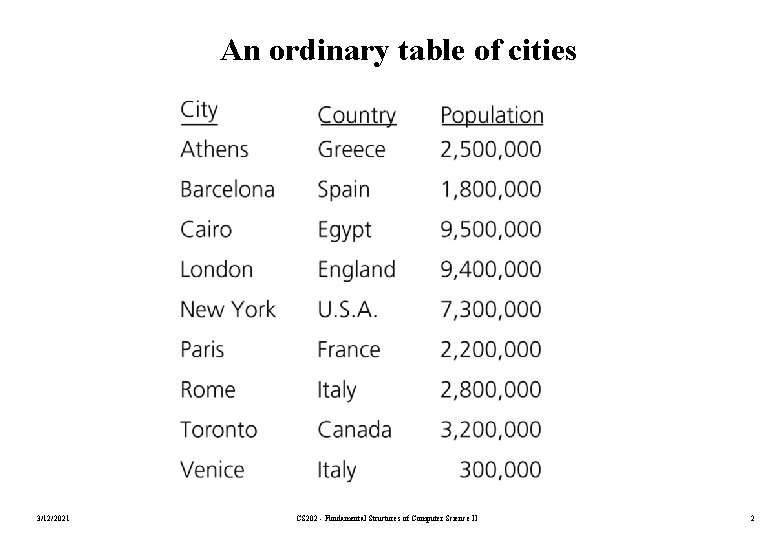
An ordinary table of cities 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 2

ADT Table Operations • Various sets of table operations are possible. Some of them are: – – – – Create an empty table. Destroy a table. Determine whether a table is empty. Determine the number of items in the table. Insert a new item into a table. Delete the item with a given search key. Retrieve the item with a given search key. Traverse the table. • The client of the ADT table may need a subset of these operations, or require more operations on the table. • Are keys in the table are unique? – We will assume that keys in our table are unique. – But, some other tables allow duplicate keys. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 3

Selecting an Implementation • Since an array or a linked list represents items one after another, these implementations are called linear. • There are four categories of linear implementations: – – Unsorted, array based (an unsorted array) Unsorted, pointer based (a simple linked list) Sorted (by search key), array based (a sorted array) Sorted (by search key), pointer based (a sorted linked list). • We have also nonlinear implementations such as binary search tree. – Binary search tree implementation offers several advantages over linear implementations. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 4

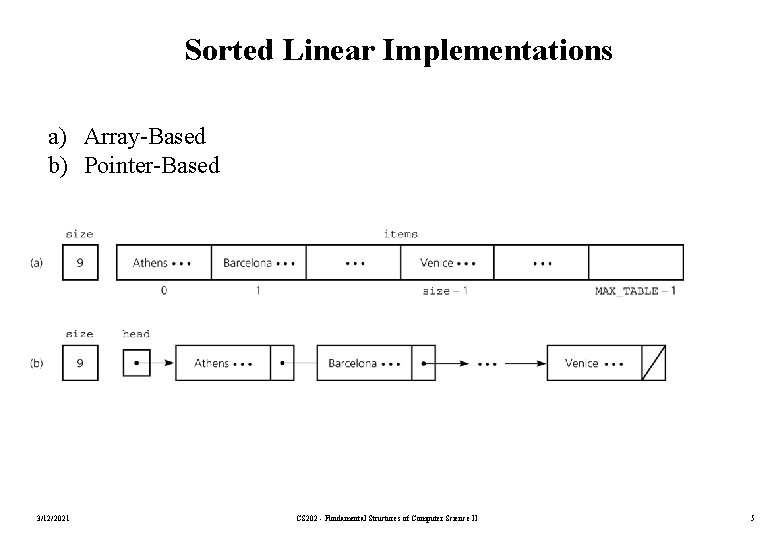
Sorted Linear Implementations a) Array-Based b) Pointer-Based 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 5

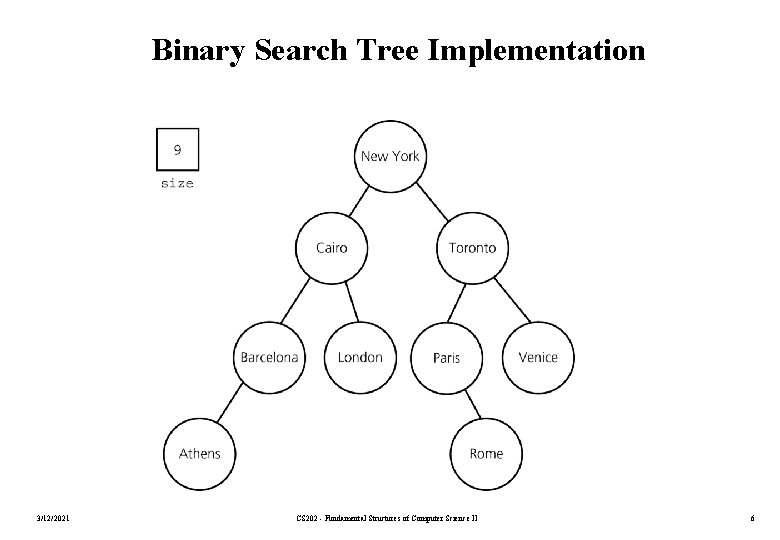
Binary Search Tree Implementation 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 6

Which Implementation should be used? • • Which implementation is appropriate depends on our application. Before we select an implementation, we should answer following questions about our application: 1. What operations are needed? – Our application may not need all operations. – Some operation is implemented more efficiently in an implementation, and another operation is implemented more efficiently in another implementation. 2. How often is each operation is required? – Some applications may require many occurrences of an operation, but other applications may not. – For example, some applications may perform many retrievals, but not so many insertions and deletions. On the other hand, other applications may perform many insertions and deletions. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 7

How to Select an Implementation – Scenario A • Let us assume that we have an application: – inserts data items into a table. – after all data items are inserted traverse this table in no particular order. – does not perform any retrieval and deletion operations. • Which implementation is appropriate for this application? – Keeping the items in a sorted order does not provide any advantage for this application. – In fact, it will be more costly for this application. Unsorted implementation will be more appropriate. • Which unsorted implementation (array-based, pointer-based)? • • • 3/12/2021 Do we know the maximum size of the table? If we know the expected size is close to the maximum size of the table an array-based will be more appropriate (because pointer-based use extra space for pointers) Otherwise, a pointer-based will be more appropriate (because too many entries will be empty in the array-based implementation) CS 202 - Fundamental Structures of Computer Science II 8

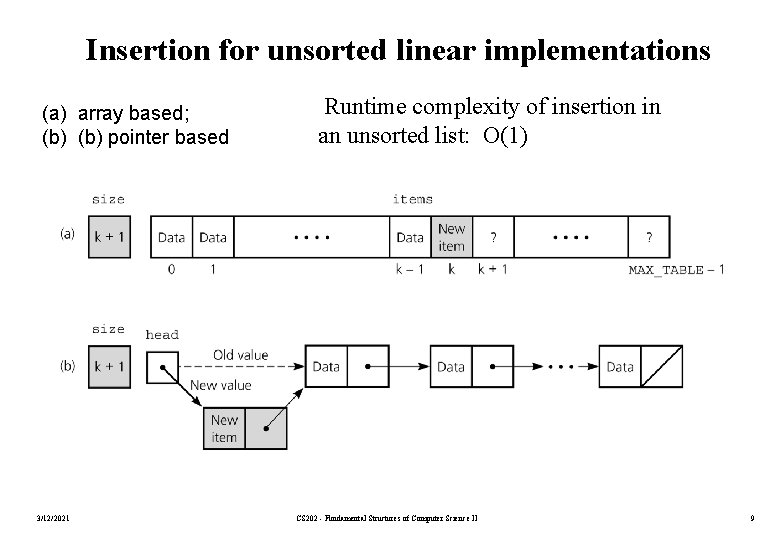
Insertion for unsorted linear implementations (a) array based; (b) pointer based 3/12/2021 Runtime complexity of insertion in an unsorted list: O(1) CS 202 - Fundamental Structures of Computer Science II 9

How to Select an Implementation – Scenario B • Let us assume that we have an application: – performs many retrievals, but no insertions and deletions (or so few insertions or deletions, so that we ignore their costs). – for example, a thesaurus (to look up synonyms of a word) • For this application, a sorted implementation is more appropriate. – If we use a sorted array, we can use binary search to access data. – Since the binary search is not practical with linked lists, sorted linked list implementation will not be appropriate. – We can also use a binary search tree (in fact, we can use a balanced binary search tree). • If we know the table’s maximum size, a sorted array-based implementation is more appropriate for frequent retrievals. • Otherwise, a binary search tree implementation will be more appropriate for frequent retrievals. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 10

How to Select an Implementation – Scenario C • Let us assume that we have an application: – performs many retrievals, insertions and deletions. ? Sorted Array Implementation: – Retrieval is efficient. – But insertion and deletion are not efficient. We have to shift data items. sorted-array implementation is not appropriate. ? Sorted Linked List Implementation: – Retrieval, insertion, and deletion are not efficient (although we do not shift data items) sorted linked list implementation is not appropriate. ? Binary Search Tree Implementation: – Retrieval, insertion, and deletion are efficient. binary search tree implementation is appropriate. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 11

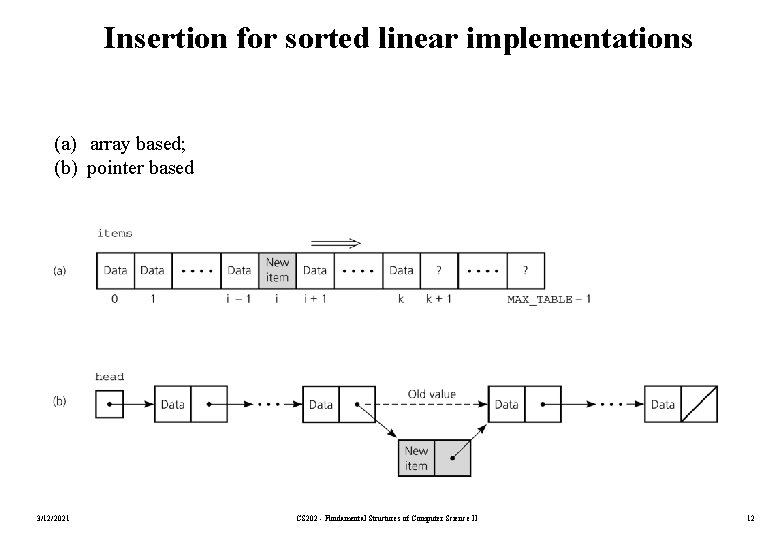
Insertion for sorted linear implementations (a) array based; (b) pointer based 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 12

Which Implementation? • Despite difficulties, linear implementations of a table can be appropriate. – Linear implementations are easy to understand, easy to implement. – Linear implementations can be appropriate for small tables. – For large tables, if there are few deletions and retrievals, linear implementations may be appropriate. • In general, a binary search tree implementation is a better choice. – Worst case: O(n) – Average case: O(log 2 n) for most table operations • Balanced binary search tree increases the efficiency of the ADT table operations. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 13

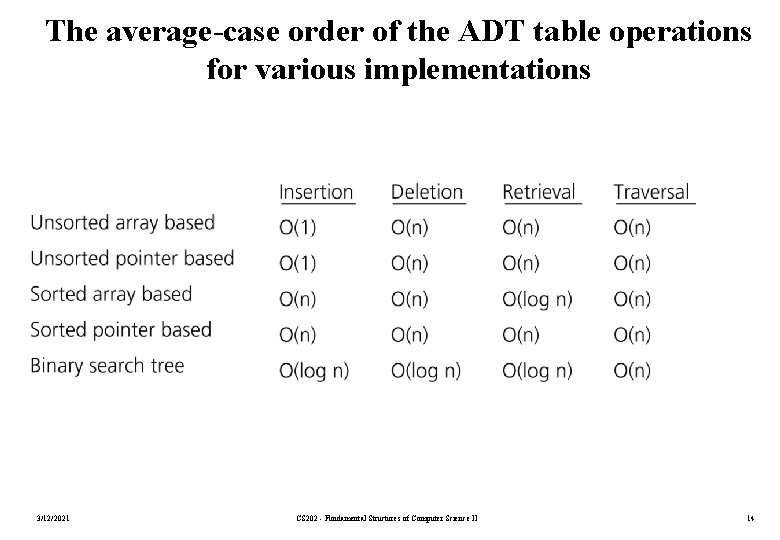
The average-case order of the ADT table operations for various implementations 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 14

Sorted Array-Based Implementation // Header file Table. A. h for the ADT table. // Sorted array-based implementation. // Assumption: A table contains at most one item with a // given search key at any time. #include "Keyed. Item. h" // definition of Keyed. Item and Key. Type #include "Table. Exception. h" const int MAX_TABLE = maximum-size-of-table; typedef Keyed. Item Table. Item. Type; typedef void (*Function. Type)(Table. Item. Type& an. Item); class Table { public: Table(); // default constructor // copy constructor and destructor are supplied by the compiler 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 15

Sorted Array-Based Implementation (cont. ) // Table operations: virtual bool table. Is. Empty() const; // Determines whether a table is empty. virtual int table. Length() const; // Determines the length of a table. virtual void table. Insert(const Table. Item. Type& new. Item)throw (Table. Exception); // Inserts an item into a table in its proper sorted // order according to the item's search key. virtual void table. Delete(Key. Type search. Key)throw (Table. Exception); // Deletes an item with a given search key from a table. virtual void table. Retrieve(Key. Type search. Key, Table. Item. Type& table. Item) const throw (Table. Exception); // Retrieves an item with a given search key from a table. virtual void traverse. Table(Function. Type visit); // Traverses a table in sorted search-key order, calling // function visit() once for each item. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 16

Sorted Array-Based Implementation (cont. ) protected: void set. Size(int new. Size); // Sets the private data member size to new. Size. void set. Item(const Table. Item. Type& new. Item, int index); // Sets items[index] to new. Item. int position(Key. Type search. Key) const; // Finds the position of a table item or its insertion point. private: Table. Item. Type items[MAX_TABLE]; // table items int size; // table size int key. Index(int first, int last, Key. Type search. Key) const; // Searches a particular portion of the private array // items for a given search key by using a binary search. }; // end Table class 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 17

table. Insert void Table: : table. Insert(const Table. Item. Type& new. Item) { // Note: Insertion is unsuccessful if the table is full, // that is, if the table already contains MAX_TABLE items. // Calls: position. if (size == MAX_TABLE) throw Table. Exception("Table. Exception: Table full"); // there is room to insert; // locate the position where new. Item belongs int spot = position(new. Item. get. Key()); // shift up to make room for the new item for (int index = size-1; index >= spot; --index) items[index+1] = items[index]; // make the insertion items[spot] = new. Item; ++size; } // end table. Insert 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 18

table. Delete void Table: : table. Delete(Key. Type search. Key) { // Calls: position. // locate the position where search. Key exists/belongs int spot = position(search. Key); // is search. Key present in the table? if ((spot > size) || (items[spot]. get. Key() != search. Key)) // search. Key not in table throw Table. Exception( "Table. Exception: Item not found on delete"); else { // search. Key in table --size; // delete the item // shift down to fill the gap for (int index = spot; index < size; ++index) items[index] = items[index+1]; } // end if } // end table. Delete 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 19

table. Retrieve void Table: : table. Retrieve(Key. Type search. Key, Table. Item. Type& table. Item) const // Calls: position. { // locate the position where search. Key exists/belongs int spot = position(search. Key); // is search. Key present in table? if ((spot > size) || (items[spot]. get. Key() != search. Key)) // search. Key not in table throw Table. Exception( "Table. Exception: Item not found on retrieve"); else table. Item = items[spot]; // item present; retrieve it } // end table. Retrieve 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 20

traverse. Table void Table: : traverse. Table(Function. Type visit) { for (int index = 0; index < size; ++index) visit(items[index]); } // end traverse. Table 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 21

Binary Search Tree Implementation – Table. B. h #include "BST. h" // binary search tree operations #include "Table. Exception. h" typedef Tree. Item. Type Table. Item. Type; class Table { public: Table(); // default constructor // copy constructor and destructor are supplied by the compiler // Table operations: virtual bool table. Is. Empty() const; virtual int table. Length() const; virtual void table. Insert(const Table. Item. Type& new. Item) throw(Table. Exception); virtual void table. Delete(Key. Type search. Key) throw(Table. Exception); virtual void table. Retrieve(Key. Type search. Key, Table. Item. Type& table. Item) const throw(Table. Exception); virtual void traverse. Table(Function. Type visit); protected: void set. Size(int new. Size); private: Binary. Search. Tree bst; // binary search tree that contains the table’s items int size; // number of items in the table }; // end Table class 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 22

Binary Search Tree Implementation – Table. B. cpp #include "Table. B. h" // header file void Table: : table. Insert(const Table. Item. Type& new. Item) { try { bst. search. Tree. Insert(new. Item); ++size; } // end try catch (Tree. Exception e) { throw Table. Exception( "Table. Exception: Cannot insert item"); } // end catch } // end table. Insert 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 23

table. Delete void Table: : table. Delete(Key. Type search. Key) { try { bst. search. Tree. Delete(search. Key); } // end try catch (Tree. Exception e) { throw Table. Exception( "Table. Exception: Item not found on delete"); } // end catch } // end table. Delete 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 24

table. Retrieve & traverse. Table void Table: : table. Retrieve(Key. Type search. Key, Table. Item. Type& table. Item) const { try { bst. search. Tree. Retrieve(search. Key, table. Item); } // end try catch (Tree. Exception e) { throw Table. Exception( "Table. Exception: Item not found on retrieve"); } // end catch } // end table. Retrieve void Table: : traverse. Table(Function. Type visit) { bst. inorder. Traverse(visit); } // end traverse. Table // End of implementation file. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 25

The ADT Priority Queue • Priority queue is a variation of the table. • Each data item in a priority queue has a priority value. • We insert an item with a priority value into its proper position in the priority queue. • Deletion in the priority queue is not same as the deletion in the table. We delete operation deletes the item with the highest priority. • Using a priority queue we prioritize a list of tasks: – Job scheduling 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 26

ADT Priority Queue Operations create. Priority. Queue() – create an empty priority queue. destroy. Priority. Queue – destroys a priority queue. is. Empty – determines whether a priority queue is empty or not. insert – Inserts a new item (with a priority value) into a priority queue. delete – retrieves the item in a priority queue with the highest priority value, and deletes that item from the priority queue. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 27

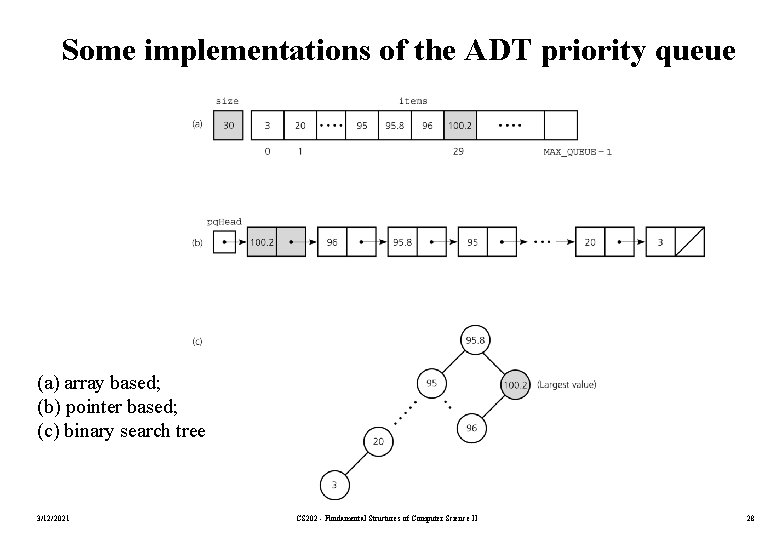
Some implementations of the ADT priority queue (a) array based; (b) pointer based; (c) binary search tree 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 28

Implementations – Analysis • None of these implementations of the priority queue is not efficient enough. Array-Based – – Insertion will be O(n) Pointer-Based – – Insertion will be O(n) BST Implementation – – Insertion is O(log 2 n) in average, but O(n) in the worst case. • We need a balanced BST so that we can get better performance ( O(logn) in the worst case) Heap 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 29

Heaps Definition: A heap is a complete binary tree such that – It is empty, or – Its root contains a search key greater than or equal to the search key in each of its children, and each of its children is also a heap. • In this definition, since the root contains the item with the largest search key, heap in this definition is also known as maxheap. • On the other hand, a heap which places the smallest search key in its root is know as minheap. • We will talk about maxheap as heap in the rest of our discussions. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 30

Difference between Heap and BST • A heap is NOT a binary search tree. Differences between heap and BST: 1. While we can see a binary search tree as sorted, but a heap is ordered in much weaker sense. • The order of the heap (although it is not sorted) is sufficient for the efficient performance of the priority queue operations. 2. While binary search trees come in many different shapes, heaps are always complete binary trees. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 31

Heap Examples 50 50 45 40 50 40 45 40 30 HEAPS 35 33 50 50 42 40 3/12/2021 45 NOT HEAPS 40 45 30 35 CS 202 - Fundamental Structures of Computer Science II 32

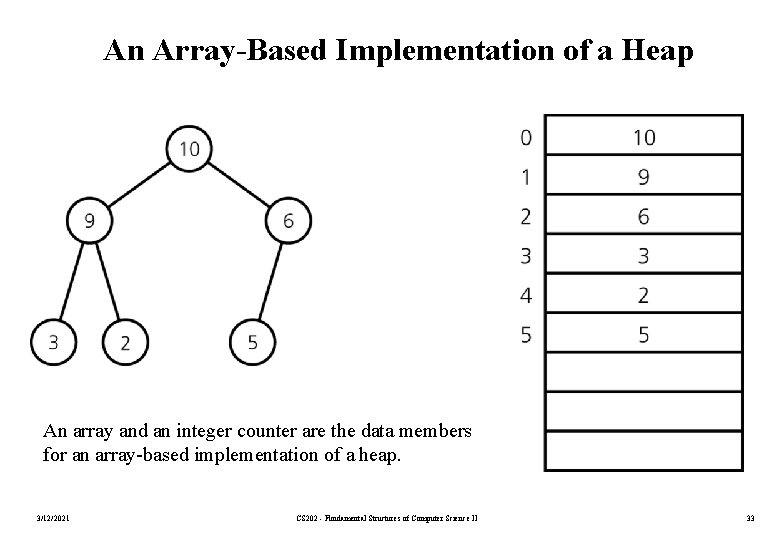
An Array-Based Implementation of a Heap An array and an integer counter are the data members for an array-based implementation of a heap. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 33

Major Heap Operations • Two major heap operations are insertion and deletion. Insertion – Inserts a new item into a heap. – After the insertion, the heap must satisfy heap properties. Deletion – Retrieves and deletes the root of the heap. – After the deletion, the heap must satisfy heap properties. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 34

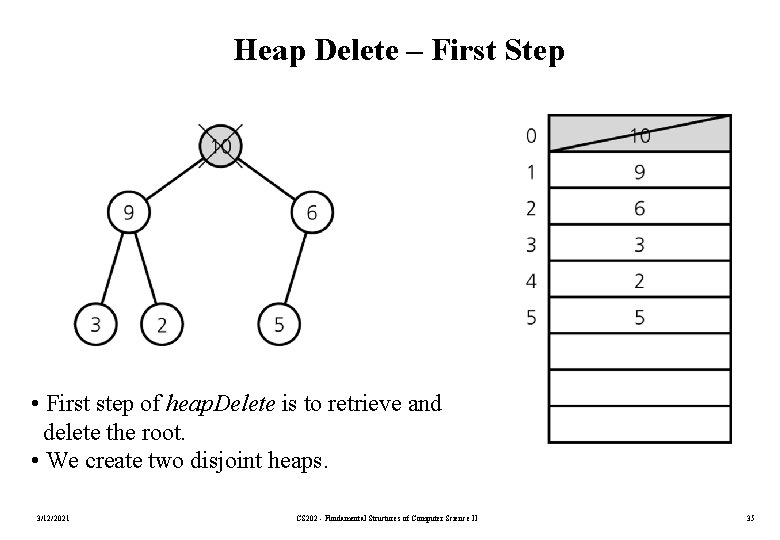
Heap Delete – First Step • First step of heap. Delete is to retrieve and delete the root. • We create two disjoint heaps. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 35

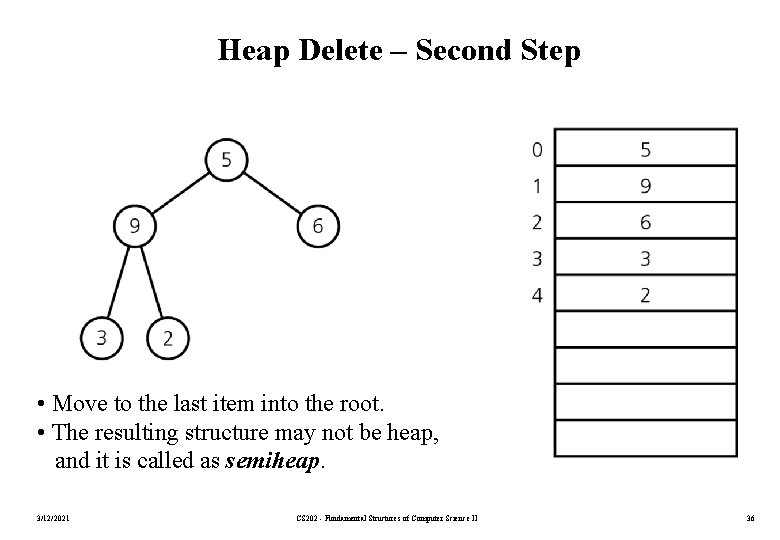
Heap Delete – Second Step • Move to the last item into the root. • The resulting structure may not be heap, and it is called as semiheap. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 36

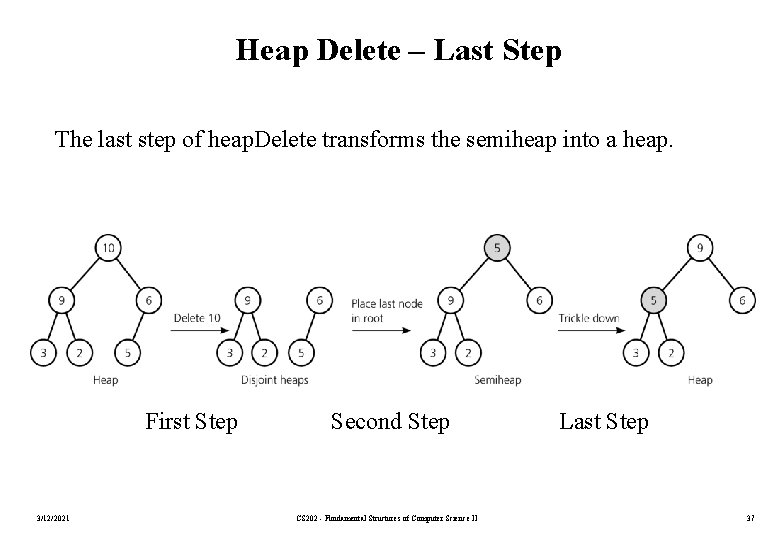
Heap Delete – Last Step The last step of heap. Delete transforms the semiheap into a heap. First Step 3/12/2021 Second Step CS 202 - Fundamental Structures of Computer Science II Last Step 37

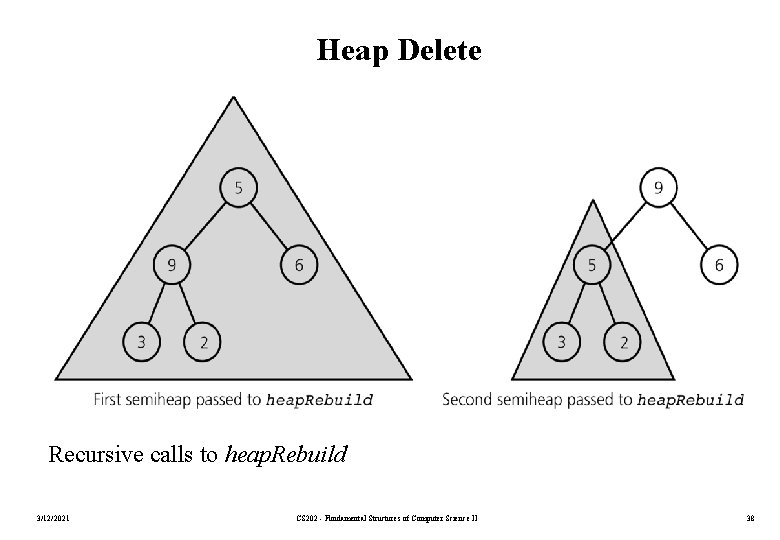
Heap Delete Recursive calls to heap. Rebuild 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 38

Heap Delete – Analysis • Since the height of a complete binary tree with n nodes is always log 2(n+1) heap. Delete is O(log 2 n) 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 39

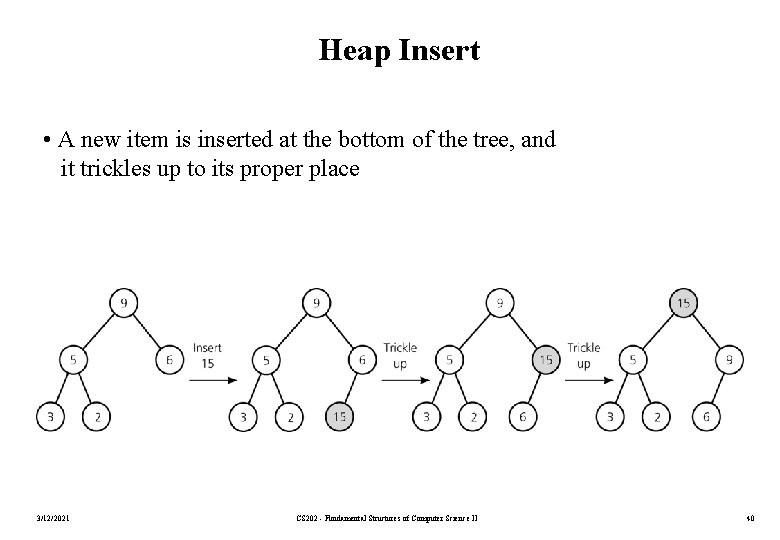
Heap Insert • A new item is inserted at the bottom of the tree, and it trickles up to its proper place 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 40

Heap Insert – Analysis • Since the height of a complete binary tree with n nodes is always log 2(n+1) heap. Insert is O(log 2 n) 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 41

Heap. h const int MAX_HEAP = maximum-size-of-heap; #include "Keyed. Item. h" // definition of Keyed. Item typedef Keyed. Item Heap. Item. Type; class Heap { public: Heap(); // default constructor // copy constructor and destructor are supplied by the compiler // Heap operations: virtual bool heap. Is. Empty() const; // Determines whether a heap is empty. virtual void heap. Insert(const Heap. Item. Type& new. Item) throw(Heap. Exception); // Inserts an item into a heap. virtual void heap. Delete(Heap. Item. Type& root. Item) throw(Heap. Exception); // Retrieves and deletes the item in the root of a heap. // This item has the largest search key in the heap. protected: void heap. Rebuild(int root); // Converts the semiheap rooted at index root into a heap. private: Heap. Item. Type items[MAX_HEAP]; // array of heap items int size; // number of heap items }; // end class 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 42

Heap. cpp // ***************************** // Implementation file Heap. cpp for the ADT heap. // ***************************** #include "Heap. h" // header file for class Heap: : Heap() : size(0) { } // end default constructor bool Heap: : heap. Is. Empty() const { return bool(size == 0); } // end heap. Is. Empty 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 43

heap. Insert void Heap: : heap. Insert(const Heap. Item. Type& new. Item) { // Method: Inserts the new item after the last item in the heap and // trickles it up to its proper position. // The heap is full when it contains MAX_HEAP items. if (size > MAX_HEAP) throw Heap. Exception("Heap. Exception: Heap full"); // place the new item at the end of the heap items[size] = new. Item; // trickle new item up to its proper position int place = size; int parent = (place - 1)/2; while ( (parent >= 0) && (items[place]. get. Key() > items[parent]. get. Key()) ) { // swap items[place] and items[parent] Heap. Item. Type temp = items[parent]; items[parent] = items[place]; items[place] = temp; place = parent; parent = (place - 1)/2; } // end while ++size; } // end heap. Insert 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 44

heap. Delete void Heap: : heap. Delete(Heap. Item. Type& root. Item) // Method: Swaps the last item in the heap with the root // and trickles it down to its proper position. { if (heap. Is. Empty()) throw Heap. Exception("Heap. Exception: Heap empty"); else { root. Item = items[0]; items[0] = items[--size]; heap. Rebuild(0); } // end if } // end heap. Delete 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 45

heap. Rebuild void Heap: : heap. Rebuild(int root) { // if the root is not a leaf and the root's search key // is less than the larger of the search keys in the root's children int child = 2 * root + 1; // index of root's left child, if any if ( child < size ) { // root is not a leaf, so it has a left child at child int right. Child = child + 1; // index of right child, if any // if root has a right child, find larger child if ( (right. Child < size) && (items[right. Child]. get. Key() > items[child]. get. Key()) ) child = right. Child; // index of larger child // if the root's value is smaller than the // value in the larger child, swap values if ( items[root]. get. Key() < items[child]. get. Key() ) { Heap. Item. Type temp = items[root]; items[root] = items[child]; items[child] = temp; // transform the new subtree into a heap. Rebuild(child); } // end if // if root is a leaf, do nothing } // end heap. Rebuild 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 46

Heap Implementation of Priority Queue • Since the heap operations and the priority queue operations are same, the heap implementation of the priority queue is straightforward. • Both insertion and deletion operations of the priority queue will be O(log 2 n), when we use the heap. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 47

PQ. h // Header file PQ. h for the ADT priority queue. // Heap implementation. #include "Heap. h" // ADT heap operations typedef Heap. Item. Type PQueue. Item. Type; class Priority. Queue { public: // default constructor, copy constructor, and // destructor are supplied by the compiler // priority-queue operations: virtual bool pq. Is. Empty() const; virtual void pq. Insert(const PQueue. Item. Type& new. Item) throw (PQueue. Exception); virtual void pq. Delete(PQueue. Item. Type& PQueue. Item. Type) throw (PQueue. Exception); private: Heap h; }; // end Priority. Queue class 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 48

PQ. cpp // Implementation file PQ. cpp for the ADT priority queue. // A heap represents the priority queue. #include "PQ. h" // header file for priority queue bool Priority. Queue: : pq. Is. Empty() const { return h. heap. Is. Empty(); } // end pq. Is. Empty void Priority. Queue: : pq. Insert(const PQueue. Item. Type& new. Item) { try { h. heap. Insert(new. Item); } // end try catch (Heap. Exception e) { throw PQueue. Exception( "PQueue. Exception: Priority queue full"); } // end catch } // end pq. Insert 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 49

pq. Delete void Priority. Queue: : pq. Delete(PQueue. Item. Type& priority. Item) { try { h. heap. Delete(priority. Item); } // end try catch (Heap. Exception e) { throw PQueue. Exception( "PQueue. Exception: Priority queue empty"); } // end catch } // end pq. Delete 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 50

Heapsort • 3/12/2021 We can use a heap to sort an array: 1. Create a heap from the given initial array with n items. 2. Swap the root of the heap with the last element in the heap. 3. Now, we have a semiheap with n-1 items, and a sorted array with one item. 4. Using heap. Rebuild convert this semiheap into a heap. Now we will have a heap with n-1 items. 5. Repeat the steps 2 -4 as long as the number of items in the heap is more than 1. CS 202 - Fundamental Structures of Computer Science II 51

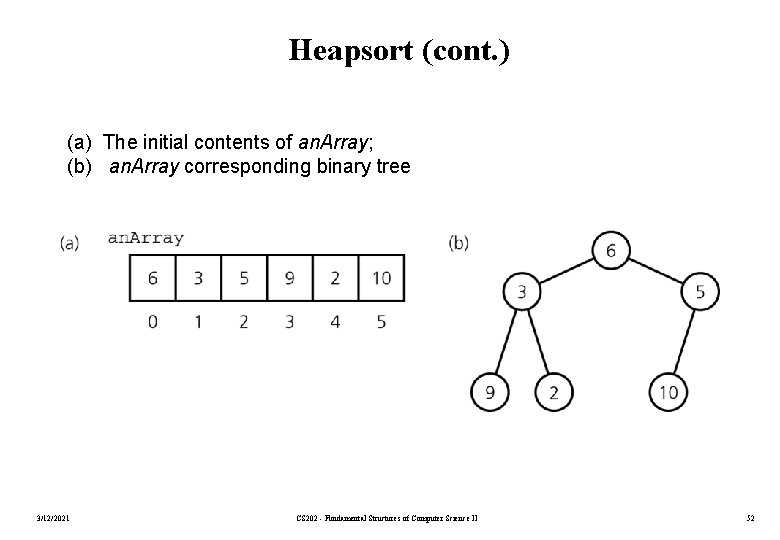
Heapsort (cont. ) (a) The initial contents of an. Array; (b) an. Array corresponding binary tree 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 52

Heapsort – Building a Heap from an array for (index = (n/2) – 1 ; index >= 0 ; index--) { // Invariant: the tree rooted at index // is a semiheap. Rebuild(an. Array, index, n) // Assertion: the tree rooted at index // is a heap. } 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 53

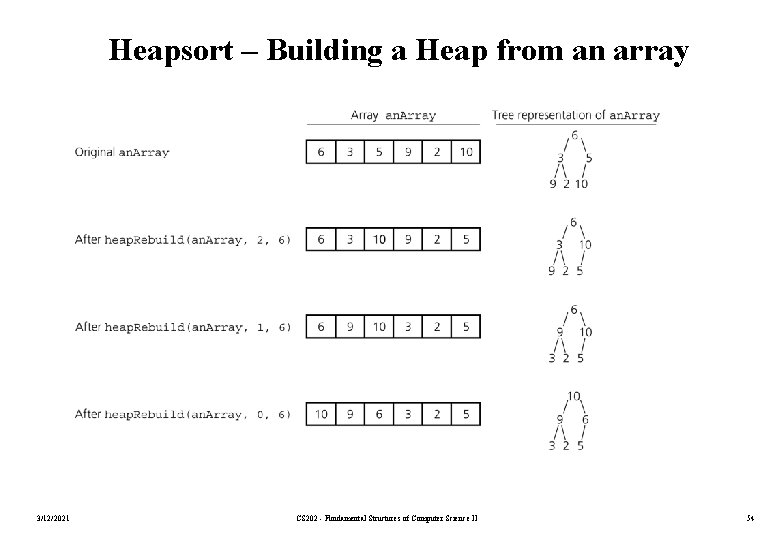
Heapsort – Building a Heap from an array 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 54

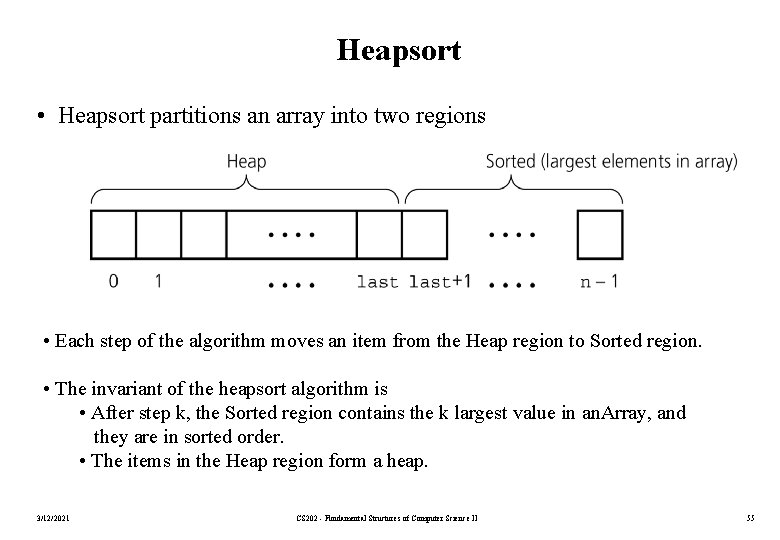
Heapsort • Heapsort partitions an array into two regions • Each step of the algorithm moves an item from the Heap region to Sorted region. • The invariant of the heapsort algorithm is • After step k, the Sorted region contains the k largest value in an. Array, and they are in sorted order. • The items in the Heap region form a heap. 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 55

Heapsort Algorithm heap. Sort(inout an. Array: Array. Type, in n: integer) { // sorts an. Array[0. . n-1] // build initial heap for (index = (n/2) – 1 ; index >= 0 ; index--) { // Invariant: the tree rooted at index is a semiheap. Rebuild(an. Array, index, n) // Assertion: the tree rooted at index is a heap. } for (last = n-1 ; last > 0 ; last--) { // Invariant: an. Array[0. . last] is a heap, an. Array[last+1. . n-1] is sorted and // contains the largest items of an. Array. // swap the largest item (an. Array[0]) and the last item in the Heap region. swap an. Array[0] and an. Array[last] // make the Heap region a heap again heap. Rebuild(an. Array, 0, last) } } 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 56

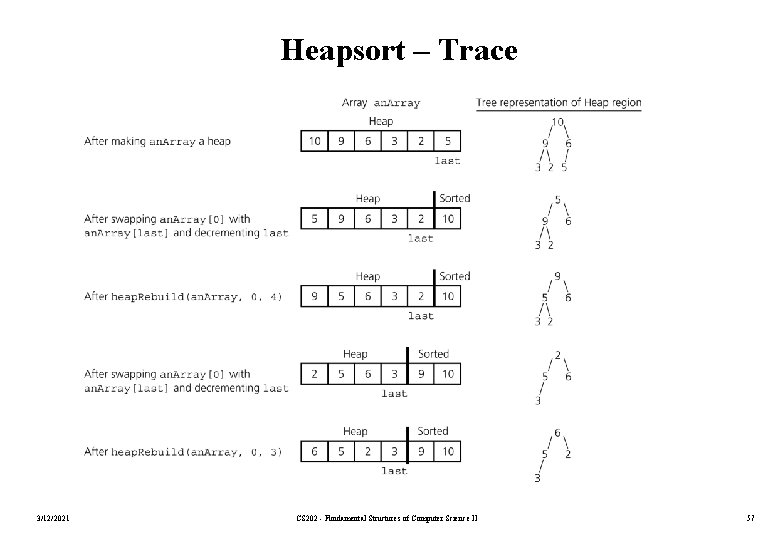
Heapsort – Trace 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 57

Heapsort – Trace 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 58

Heapsort – Analysis • Heapsort is O(n * log n) at average case at worst case • Heapsort is slower than quicksort at average case, but its worst case is also O(n * log n). 3/12/2021 CS 202 - Fundamental Structures of Computer Science II 59