Adsorption Catalysis Diagenesis Lecture 19 Langmuir Isotherm is

Adsorption Catalysis Diagenesis Lecture 19

Langmuir Isotherm • is known as the Langmuir Isotherm o named for Irving Langmuir, who worked for GE. • We can also express this in terms of the adsorption density, Γ: • At large concentration then

Freundlich Isotherm • At low concentration, • In other words, fraction of sites occupied by M is proportional to concentration. • This is known as the Freundlich Isotherm. • We’ll return to this in the next chapter. Red curve shows adsorption of Sr on Fe. OOH calculated from Langmuir Isotherm. Inset shows linear Freunlich behavior at low concentration (notice difference in units).

Adsorption and Catalysis • • • Catalysis quite frequency involves adsorption of species on solid surfaces. An everyday example is the catalytic converters in exhaust systems of cars. In these, gaseous species are adsorbed to a noble metal surface (e. g. , palladium) to catalyze reactions such as NOx → N 2 + x. O 2 Mineral surfaces are thought to have been important in the initiation of terrestrial life by catalyzing critical organic compounds from inorganic ones such as methane, N 2, etc.

Catalysis • The International Union of Pure and Applied Chemistry (IUPAC) defines catalyst as follows: A catalyst is a substance that increases the rate without modifying the overall standard Gibbs energy change in the reaction; the process is called catalysis, and a reaction in which a catalyst in involved is known as a catalyzed reaction. • Catalysts work by providing an alternative reaction path with lower activation energy. In many cases, the lowering of the activation energy arises when reacting species are adsorbed. The heat liberated by the adsorption (∆Hads) is available to contribute toward the activation energy.

Example: oxidation of 5+ to V by Ti. O 2 4+ V • Surfaces of many metal oxides and sulfides can catalyze oxidation-reduction reactions by conducting electrons (i. e. , serving as an electrode). • As we’ll see, a metal oxide immersed in water would adsorb H+ and OH– to the surface (> designates a surface): >Ti+ + H 2 O ⇋ >Ti. OH +

Vanadium Oxidation • Oxidation of vanadyl proceeds as follows (> designates a surface): 2>Ti. OH + VO 2+ ⇋ >(Ti. O)2 VO + 2 H+ >(Ti. O)2 VO + >Ti. OH ⇋ >(Ti)3 VO 4 +e– + H+ >Ti 3 VO 4 + 3 H 2 O ⇋ 3>Ti. OH + HVO 42– + 2 H+

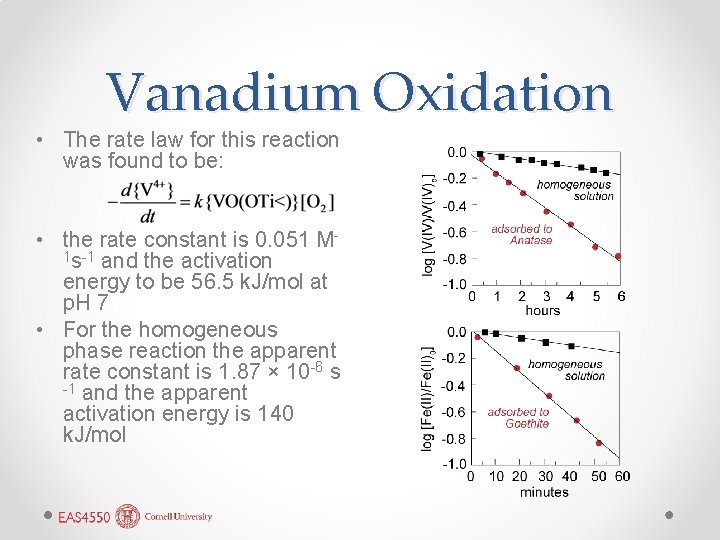
Vanadium Oxidation • The rate law for this reaction was found to be: • the rate constant is 0. 051 M 1 s-1 and the activation energy to be 56. 5 k. J/mol at p. H 7 • For the homogeneous phase reaction the apparent rate constant is 1. 87 × 10 -6 s -1 and the apparent activation energy is 140 k. J/mol

Diagenesis is the transformation of a sediment into a sedimentary rock. Physical processes involve compaction and expulsion of water as the sediment is buried. We’ll briefly consider some of the chemical processes that accompany this.

• Consider a sedimentary layer ‘A’ being buried as sediment accumulates above it. • We can chose a reference frame fixed to the layer, or to the sediment-water interface. • In the latter case, the layer will appear to move downward with time. • Change in concentration with time at some fixed depth x is then: • First term on the right is any changes in concentration within layer, second term is the concentration gradient times the burial rate, ω. • We can use this equation to change reference frames.

Steady-State Case • This is the case where: • Solving, we have: • In this case, the concentration in the sediment at the surface is constant, but diagenetic changes result in decrease in concentration with time. But concentration at a fixed depth is constant. The diagenetic changes impose a concentration gradient. •

No diagenesis • This is the case where • so that • Change in concentration at some fixed depth is the burial rate times the gradient.

Diagenetic Process • Sediment consists of particles plus ‘pore water’. If porosity is �� then fraction of particles is 1 - ��. • As weight of sediment accumulating above increases, water tends to be expelled - resulting in upward velocity of pore fluid. • In addition, dissolution and cementation (precipitation) can change porosity. • Due to compaction, rate of burial will not be equal to sedimentation rate.

Fluxes and Bioturbation • • Now imagine a layer of sediment of thickness dx. There are fluxes into and out of this layer due to: o o o Water advection Chemical diffusion Bioturbation • • Advective Flux is simply J = v. Ci We can treat the biodiffusive flux the same as chemical diffusion: • A difference is that the biodiffusive flux is likely to be a function of depth since most animals live near the surface (and O 2 generally decreases with depth). • For biodiffusion, Fick’s Second Law becomes:

Diffusion and Porosity • Diffusion is so much faster through the pore water than through solids, the latter can be effectively ignored. • Thus we can view the ‘molecular flux’ - the chemical one we have already discussed, as reduced to that occurring through pores: • Fick’s Second Law becomes

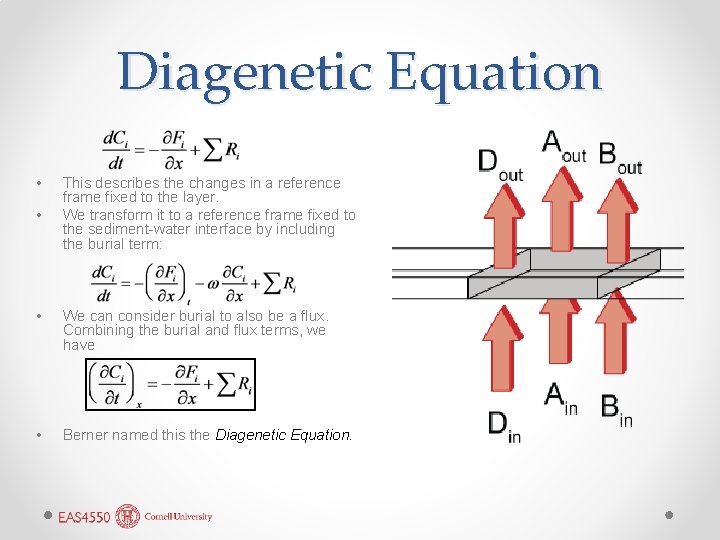
Diagenetic Equation • Thinking again about our layer, conservation of mass dictates that the concentration of i will change if the fluxes of i in are different than the fluxes out: o F is the sum of the three fluxes • Concentration may also occur as a result of reactions involving i, Ri occurring within the layer. • Overall then

Diagenetic Equation • • This describes the changes in a reference frame fixed to the layer. We transform it to a reference frame fixed to the sediment-water interface by including the burial term: • We can consider burial to also be a flux. Combining the burial and flux terms, we have • Berner named this the Diagenetic Equation.

Example: Reduction of Sulfate • Sulfate is abundant in seawater and will be reduced by bacteria to sulfide once O 2 is exhausted to metabolize organic matter. We assume the (only) reaction is: 2 CH 2 O + SO 42 - = H 2 S + 2 HCO 3 • Assume the rate of reaction depends of availability of organic matter: • Assuming steady-state • Then • Integrating:

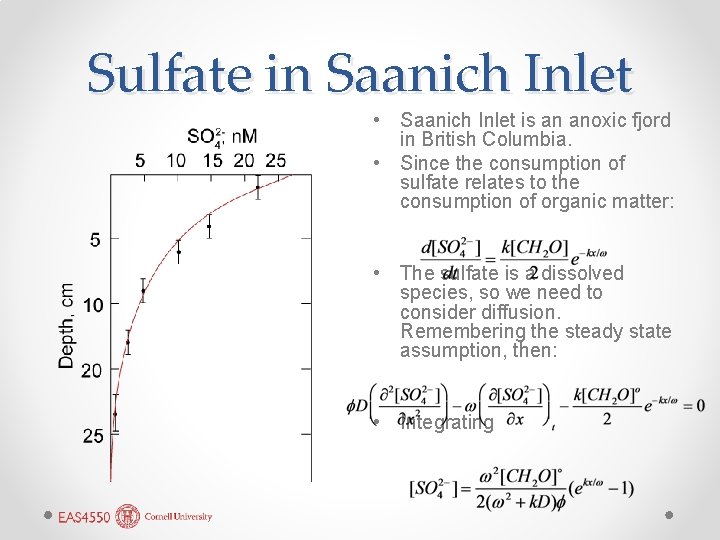
Sulfate in Saanich Inlet • Saanich Inlet is an anoxic fjord in British Columbia. • Since the consumption of sulfate relates to the consumption of organic matter: • The sulfate is a dissolved species, so we need to consider diffusion. Remembering the steady state assumption, then: • Integrating

Aquatic Chemistry Chapter 6 Introduction

Water is virtually omnipresent at the surface of the Earth. Consequently, there is continual reaction between water and materials at the surface (rocks, soil, atmosphere, life). As a consequence of these reactions, water is never pure (though often pure enough that we will find it convenient to assume its mole fraction is 1). We’ll now apply our tools of physical chemistry to the problem of aqueous solutions and their interaction with the atmosphere and, particularly, the solid Earth.

Aquatic Reactions • Acid-Base H 2 CO 3 ⇋ H+ + HCO 3– • Complexation Hg 2+ + H 2 O ⇋ Hg(OH) - + H+ • Dissolution/Precipitation KAl. SI 3 O 8 + H+ + 7 H 2 O ⇋ Al(OH)3 + K+ + 3 H 4 Si. O 4 • Adsorption/Desorption ≡S + Mn 2+ ⇋ ≡S–Mn • We’ll consider each of these in turn.

Acid-Base Reactions

Importance of Acid-Base Reactions • The hydrogen and hydroxide ions are often participants in all the foregoing reactions. • As a result, these reactions are p. H-dependent. o In order to characterize the state of an aqueous solution, that is, for example, to determine how much Ca. CO 3 a solution will dissolve, the complexation state of metal ions, or the redox state of Mn, the first step is usually to determine p. H. • On a larger scale, weathering of rock and precipitation of sediments depend critically on p. H. • Thus p. H is sometimes called the master variable in aquatic systems. • If the p. H is known, the concentration of OH– is also known since [OH–][H+] = 10 -14 o at 25˚C. (Strictly speaking, it is the product of activities equal to 10 -14. For simplicity, we will often assume ideality.

Defining Acids and Bases • Arrhenius defined an acid as a substance that upon solution in water releases free protons. He defined a base is a substance that releases hydroxide ions in solution. • Chemists generally prefer the definition of Brønstead, who defined acid and base as proton donors and proton acceptors respectively. • The strength of an acid or base is measured by its tendency to donate or accept protons. The dissociation constant for an acid or base is a quantitative measure of its strength. For example, dissociation of HCl: HCl ⇋ H+ + Cl- • This is a strong acid because only about 3% remains undissociated. • In contrast, for • Kdiss = 10 -7; very few hydrogens generally dissociate (except in very allkaline solution). H 2 S ⇋ H+ + HS–

Amphoteric Behavior • Metal hydroxides can either donate or accept protons, depending upon p. H. For example, we can represent this in the case of aluminum as: Al(OH)2+ + H+ ⇋ Al(OH)2+ +H 2 O Al(OH)2+ + OH– ⇋ Al(OH)3 • Metals dissolved in water are always surrounded by solvation shells. The positive charges of the hydrogens in the surrounding water molecules are to some extent repelled by the positive charge of the metal ion. For this reason, water molecules in the solvation shell are more likely to dissociate and give up a proton more readily than other water molecules. Thus the concentration of such species will affect p. H.