Administrative stuff On Thursday we will start class

Administrative stuff • On Thursday, we will start class at 11: 10, and finish at 11: 55 • This means that each project will get a 10 minute presentation + 5 minutes of questions and answers

Pred. abstraction for software verification • Won’t go into details of paper • This work is interesting from the perspective of this class because it ties together two techniques we’ve already seen: – ESC/Java style checking – Predicate abstraction (BLAST lecture given by Ranjit)

Curry-Howard Isomorphism

But before: Type systems 101

Simply typed lambda calculus • Consider the simply typed lambda calculus: e : : = n (integers) |x (variables) | x: . e (function definition) | e 1 e 2 (function application) : : = int (integer type) | 1 ! 2 (function type)

Typing rules • Typing judgment: ` e: • Is read as: in context , e has type • The context tells us what the type of the free variables in e are • Example: x: int , f: int ! int ` (f x): int • Typing rules: Judgment 1 Judgment 2

Rules for lambda terms ` (f x): 2

Rules for lambda terms ` ( x: 1. b):

What other rules do we need?

What other rules do we need? x: 2 ` x: ` n: int

Summary so far x: 2 ` x: , x: 1 ` b: 2 ` ( x: 1. b): 1 ! 2 ` n: int ` f: 1 ! 2 ` x: 1 ` (f x): 2

Adding pairs e : : = n | x | x: . e | e 1 e 2 : : = int | 1 ! 2

Adding pairs e : : = n | x | x: . e | e 1 e 2 | (e 1, e 2) (pair construction) | fst e (select first element of a pair) | snd e (select second element of a pair) : : = int | 1 ! 2 | 1 * 2 (pair type)

Rules for pairs ` (x, y): 1 * 2

Rules for pairs ` fst x: 1 ` snd x: 2

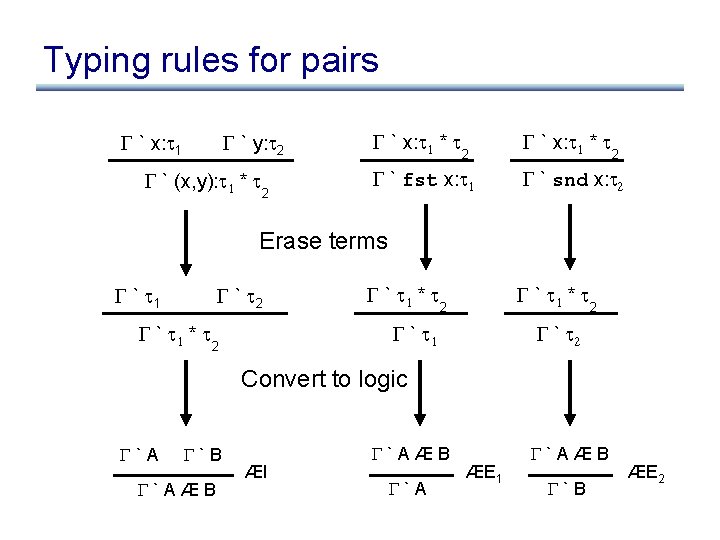
Rules for pairs (summary) ` x: 1 ` y: 2 ` (x, y): 1 * 2 ` x: 1 * 2 ` fst x: 1 ` snd x: 2

Adding unions e : : = n | x | x: . e | e 1 e 2 | (e 1, e 2) | fst e | snd e : : = int | 1 ! 2 | 1 * 2

Adding unions e : : = n | x | x: . e | e 1 e 2 | (e 1, e 2) | fst e | snd e | inl e (create a union of the left case) | inr e (create a union of the right case) | case e of inl x ) e 1 | inr y ) e 2 (perform case analysis on union) : : = int | 1 ! 2 | 1 * 2 | 1 + 2 (sum (aka union) type)

Rules for unions ` inl x: 1 + 2 ` inr x: 1 + 2

Rules for unions ` z: 1 + 2 ` (case z of inl x ) b 1 | inr y ) b 2) :

Rules for unions (summary) ` x: 1 ` inl x: 1 + 2 ` z: 1 + 2 , x: 1 ` b 1 : ` y: 2 ` inr x: 1 + 2 , y: 2 ` b 2 : ` (case z of inl x ) b 1 | inr y ) b 2) :

Curry-Howard Isomorphism

Typing rules for lambda terms , x: 1 ` b: 2 ` ( x: 1. b): 1 ! 2 ` f: 1 ! 2 ` x: 1 ` (f x): 2 Where have we seen these rules before?

Typing rules for lambda terms , x: 1 ` b: 2 ` f: 1 ! 2 ` ( x: 1. b): 1 ! 2 ` x: 1 ` (f x): 2 Erase terms ` 1 ! 2 , 1 ` 2 ` 1 ! 2 ` 1 ` 2 Convert to logic , A ` B `A)B )I `A)B `A `B )E

Typing rules for pairs ` x: 1 ` y: 2 ` (x, y): 1 * 2 ` x: 1 * 2 ` fst x: 1 ` snd x: 2 Where have we seen these rules before?

Typing rules for pairs ` x: 1 ` y: 2 ` (x, y): 1 * 2 ` x: 1 * 2 ` fst x: 1 ` snd x: 2 Erase terms ` 1 ` 2 ` 1 * 2 ` 1 ` 2 Convert to logic `A `B `AÆB ÆI `AÆB `A ÆE 1 `AÆB `B ÆE 2

Typing rules for unions ` x: 1 ` inl x: 1 + 2 ` y: 2 ` inr x: 1 + 2 Where have we seen these rules before?

Typing rules for unions ` y: 2 ` x: 1 ` inl x: 1 + 2 ` inr x: 1 + 2 Erase terms ` 1 ` 2 ` 1 + 2 Convert to logic `A `AÇB ÇI 1 `B `AÇB ÇI 2

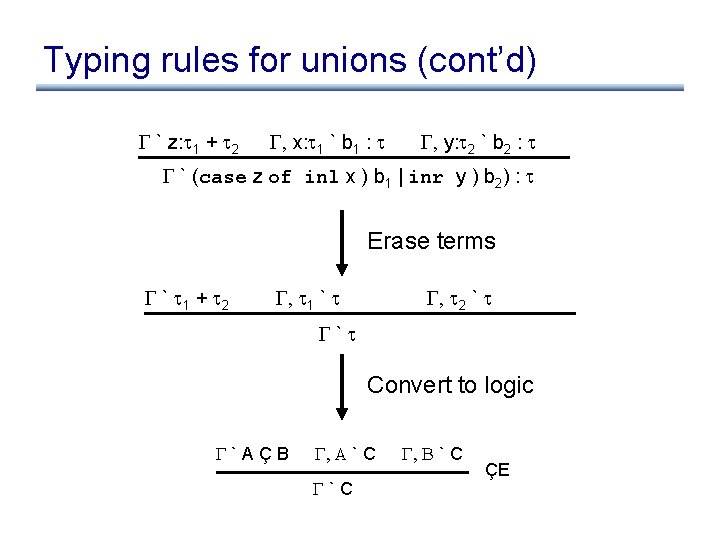
Typing rules for unions (cont’d) ` z: 1 + 2 , x: 1 ` b 1 : , y: 2 ` b 2 : ` (case z of inl x ) b 1 | inr y ) b 2) : Where have we seen this rule before?

Typing rules for unions (cont’d) ` z: 1 + 2 , x: 1 ` b 1 : , y: 2 ` b 2 : ` (case z of inl x ) b 1 | inr y ) b 2) : Erase terms ` 1 + 2 , 1 ` , 2 ` ` Convert to logic `AÇB , A ` C `C , B ` C ÇE

Curry-Howard isomorphism • Propositions-as-types : : : = int | 1 ! 2 | 1 * 2 | 1 + 2 A : : = p | A 1 ) A 2 | A 1 Æ A 2 | A 1 Ç A 2 • If types are propositions, then what are lambda terms?

Typing rules using logic for types , x : A ` y : B )I ` ( x : A. y) : A ) B `x: A `y: B ` (x, y) : A Æ B ` inl x : A Ç B `x: A ` (f x) : B `x: AÆB ÆI `x: A `z: AÇB `f: A)B ` fst x : A ÇI 1 , x : A ` e 1 : C ÆE 1 `x: AÆB ` snd x : B `y: B ` inr x : A Ç B , y: B ` e 2 : C ` (case z of inl x ) e 1 | inr y ) e 2) : C )E ÇI 2 ÇE ÆE 2

Curry-Howard isomorphism • If types are propositions, then what are lambda terms? • Answer: terms are proofs • Programs-as-proofs: ` e: A means that under assumptions , A holds and has proof e

Example , x : A ` y : B ` ( x : A. y) : A ) B )I • A proof of A ) B is a function that takes a parameter x of type A (that is to say, a proof of A), and returns something of type B (that is to say, a proof of B)

Another example `f: A)B `x: A ` (f x) : B )E • Suppose we have a proof of A ) B. This is a function f that, given a proof of A, returns a proof of B. • Suppose also that we have a proof of A, call it x. • Then applying f to x gives us a proof of B.

Another example `x: A `y: B ` (x, y) : A Æ B ÆI • A proof of A Æ B is just a pair containing the proof of A and the proof of B

Another example `x: A ` inl x : A Ç B ÇI 1 • Given a proof of A, a proof of A Ç B is a union in the left case, which records that we attained the disjunction through the left of the Ç • There is a problem though…

Another example `x: A ` inl x : A Ç B ÇI 1 • Given a proof of A, a proof of A Ç B is a union in the left case, which records that we attained the disjunction through the left of the Ç • Unfortunately, the proof does not record what the right type of the union is. – Given that x is a proof of A, what is inl x a proof of? • Ideally, we would like the proof (lambda term) to determine the formula (type). What’s the fix?

The fix for Ç proofs (union terms) • Ideally, we would like the proof (lambda term) to determine the formula (type). What’s the fix? `x: A ` inl x : A Ç B ÇI 1 `y: B ` inr x : A Ç B ÇI 2

The fix for Ç proofs (union terms) • Ideally, we would like the proof (lambda term) to determine the formula (type). What’s the fix? • We add the other type to the Ç proof (union term): `x: A ` inl. B x : AÇB ÇI 1 `y: B ` inr. A x : AÇB ÇI 2

Intuition for quantifiers • A proof of 8 x: . P(x) is a function that, given a parameter x of type , returns a proof of P(x) • A proof of 9 x: . P(x) is a function that computes a value of type for which P(x) holds • Note that 8 x: . P(x) and 9 x: . P(x) are formulas, and so they are types. But they also contain a type inside of them.

Programs-as-proofs • The programs-as-proofs paradigm is operational: to prove something, we have to provide a program • This program, when run, produces a computational artifact that represents a proof of the formula – the program itself is also a representation of the proof, but so is the final result computed by the program

Curry-Howard breaking down • Because of the operational nature of the programs-as-proofs paradigm, the paradigm only works for proofs that are constructive • Consider the formula 9 x. P(x) – A constructive proof must show to compute the x that makes the formula valid – A proof by contradiction would assume 8 x. : P(x), and then derive false. – But this does not give us a way to compute x, which means it doesn’t give us a “program-as-proofs” proof.

Curry-Howard breaking down • Curry-Howard isomorphism only holds for constructive logics – Like classical logic, except that we do not allow proofs by contradiction • The rule that you remove depends on the calculus you’re using – In our natural deduction calculus, remove the following rule: `: : A `A : E

Constructive logic • In other calculii, it may be the following rule: , : A ` F `A • Or it may be the law of the excluded middle: `AÇ: A

Constructive logic example • Consider the task of constructing an algorithm that prints 0 if Riemann’s Hypothesis holds and prints 1 otherwise. – Riemann’s Hypothesis has not been proved or disproved (Fermat’s last theorem was previously used, until it was proven…) • Does such an algorithm exists?

Constructive logic example • Consider the task of constructing an algorithm that prints 0 if Riemann’s Hypothesis holds and prints 1 otherwise. – Riemann’s Hypothesis has not been proved or disproved (Fermat’s last theorem was previously used, until it was proven…) • Does such an algorithm exists? – Classicists: yes – Constructivists: don’t know yet. Need to wait until Riemann’s Hypothesis is proven or disproven

Constructive logic • It may seem that using constructive logic is like tying your hands behind your back before starting a proof. So why use it? • Several arguments for it, including philosophical ones • One of the concrete arguments in favor of constructive logic is the Curry-Howard isomorphism, which leads to the so-called specifications-as-programs paradigm.

Specifications as programs • Suppose we want to program an algorithm that given a natural number x produces a natural number y so that a decidable condition P(x, y) is satisfied • A proof of 8 x. 9 y. P(x, y) in constructive logic yields a program for computing y from x, which is a provably correct implementation of the specification. • Programs and specifications are the same!

Specifications as programs • This idea has been used in various contexts, including two widely know theorem provers – Coq – Nu. PRL • One of the main challenges in these systems is extracting efficient programs from the proofs

Conclusion

The course in a nutshell • Logics • Techniques • Applications

Logics • Propositional, first-order, higher-order • Expressiveness, level of automation, human friendliness • Constructive logic

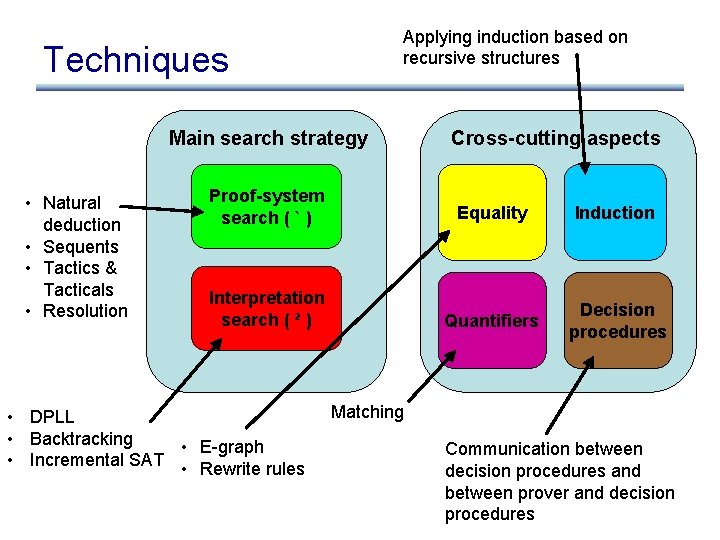
Applying induction based on recursive structures Techniques Main search strategy • Natural deduction • Sequents • Tactics & Tacticals • Resolution Cross-cutting aspects Proof-system search ( ` ) Equality Induction Interpretation search ( ² ) Quantifiers Decision procedures • DPLL • Backtracking • E-graph • Incremental SAT • Rewrite rules Matching Communication between decision procedures and between prover and decision procedures

Applications • Rhodium • ESC/Java • Blast • Proof Carrying Code

What have we learned?