Administrative Sep 20 today HW 1 due Sep

Administrative Sep. 20 (today) – HW 1 due Sep. 21 8 am – problem session Sep. 25 – HW 3 (=QUIZ #1) due Sep. 27 – HW 4 due Sep. 28 8 am – problem session Oct. 2 Oct. 4 – QUIZ #2 (pages 45 -79 of DPV)

Merge 2 sorted lists MERGE INSTANCE: 2 lists xi, yi such that x 1 x 2 … xn y 1 y 2 … ym SOLUTION: ordered merge

Merge 2 sorted lists 1 2 3 4 5 6 7 i 1, j 1 while i n and j n do if xi yj then output xi, i i + 1 else output yj, j j + 1 output remaining elements

Mergesort MERGE-SORT(a, l, r) if l < r then m (l+r)/2 MERGE-SORT(a, I, m) MERGE-SORT(a, m+1, r) MERGE(a, l, m, r)

Mergesort Running time?

Mergesort Running time? [. . . n … ] [ … n/2 … ] [ … n/4 … ] Depth = log n [ … n/2 … ] [ … n/4 … ]

Mergesort Time spent on merge? [. . . n … ] [ … n/2 … ] [ … n/4 … ] Depth = log n [ … n/2 … ] [ … n/4 … ]

Mergesort Time spent on merge? [. . . n … ] [ … n/2 … ] O(n) [ … n/2 … ] [ … n/4 … ] Depth = log n O(n) [ … n/4 … ] O(n) O(n. logn)

Mergesort recurrence T(n)= T(n/2) + (n) T(1)= (1) if n>1

Recurrences T(n) T( n/2 ) + c. n We “showed” : T(n)=O(n log n) for T(n) 2 T( n/2 ) + c. n

Recurrences T(n) 2 T( n/2 ) + c. n T(1) = O(1) Proposition: T(n) d. n. lg n Proof: T(n) 2 T( n/2 ) + c. n 2 d (n/2). lg (n/2) + c. n = d. n. ( lg n – 1 ) + cn = d. n. lg n + (c-d). n d. n. lg n

Recurrences T(n) T( n/2 ) + c. n T(n) 2 T( n/2 ) + c. n G(n) = T(n+2) T( n/2 +1) + c. n = G( n/2 -1) + c. n

Recurrences • useful • guess – substitute (prove) • or use “Master theorem” T(n) = a T(n/b) + f(n) • If f(n) = O(nc- ) then T(n) = (nc) • If f(n) = (nc) then T(n) = (nc. log n) • If f(n) = (nc+ ) then T(n)= (f(n)) if a. f(n/b) d. f(n) for some d<1 and n>n 0 c=logb a

Karatsuba-Offman a=2 n/2 a 1 + a 0 b=2 n/2 b 1 + b 0 ab=(2 n/2 a 1+a 0)(2 n/2 b 1+b 0) = 2 n a 1 b 1 + 2 n/2 (a 1 b 0 + a 0 b 1) + a 0 b 0

Karatsuba-Offman a=2 n/2 a 1 + a 0 b=2 n/2 b 1 + b 0 Multiply(a, b, n) if n=1 return a*b else R 1 Multiply(a 1, b 1, n/2) R 2 Multiply(a 0, b 1, n/2) R 3 Multiply(a 1, b 0, n/2) R 4 Multiply(a 0, b 0, n/2) return 2 n R 1+ 2 n/2 (R 2+R 3) + R 4

Karatsuba-Offman Multiply(a, b, n) if n=1 return a*b else R 1 Multiply(a 1, b 1, n/2) R 2 Multiply(a 0, b 1, n/2) R 3 Multiply(a 1, b 0, n/2) R 4 Multiply(a 0, b 0, n/2) return 2 n R 1+ 2 n/2 (R 2+R 3) + R 4 Recurrence?

Karatsuba-Offman Multiply(a, b, n) if n=1 return a*b else R 1 Multiply(a 1, b 1, n/2) R 2 Multiply(a 0, b 1, n/2) R 3 Multiply(a 1, b 0, n/2) R 4 Multiply(a 0, b 0, n/2) return 2 n R 1+ 2 n/2 (R 2+R 3) + R 4 Recurrence? T(n) = 4 T(n/2) + O(n)

Karatsuba-Offman T(n) = 4 T(n/2) + O(n) T(n)=O(n 2)

Karatsuba-Offman ab=(2 n/2 a 1+a 0)(2 n/2 b 1+b 0) = 2 n a 1 b 1 + 2 n/2 (a 1 b 0 + a 0 b 1) + a 0 b 0 Can compute in less than 4 multiplications?

Karatsuba-Offman ab=(2 n/2 a 1+a 0)(2 n/2 b 1+b 0) = 2 n a 1 b 1 + 2 n/2 (a 1 b 0 + a 0 b 1) + a 0 b 0 Can compute using 3 multiplications: (a 0+a 1)(b 0+b 1) = a 0 b 0 + (a 1 b 0 + a 0 b 1) + a 1 b 1

Karatsuba-Offman Multiply(a, b, n) if n=1 return a*b else R 1 Multiply(a 1, b 1, n/2) R 2 Multiply(a 0, b 0, n/2) R 3 Multiply(a 1+a 0, b 1+b 0, n/2+1) R 4 R 3 – R 2 – R 1 return 2 n R 1+ 2 n/2 R 3 + R 2 Recurrence?

Karatsuba-Offman Multiply(a, b, n) if n=1 return a*b else R 1 Multiply(a 1, b 1, n/2) R 2 Multiply(a 0, b 0, n/2) R 3 Multiply(a 1+a 0, b 1+b 0, n/2+1) R 4 R 3 – R 2 – R 1 return 2 n R 1+ 2 n/2 R 3 + R 2 Recurrence? T(n) = 3 T(n/2) + O(n)

Recurrences T(n) = a T(n/b) + f(n) c=logb a • If f(n) = O(nc- ) then T(n) = (nc) • If f(n) = (nc) then T(n) = (nc. log n) • If f(n) = (nc+ ) then T(n)= (f(n)) if a. f(n/b) d. f(n) for some d<1 and n>n 0 T(n) = 3 T(n/2) + (n) T(n) = 2 T(n/2) + (n. log n)

Karatsuba-Offman T(n) = 3 T(n/2) + O(n) T(n)=O(n. C) C=log 2 3 1. 58

Finding the minimum min A[1] for i from 2 to n do if A[i]<min then min A[i] How many comparisons?

Finding the minimum How many comparisons? comparison based algorithm: The only allowed operation is comparing the elements

Finding the minimum

Finding the k-th smallest element k = n/2 = MEDIAN

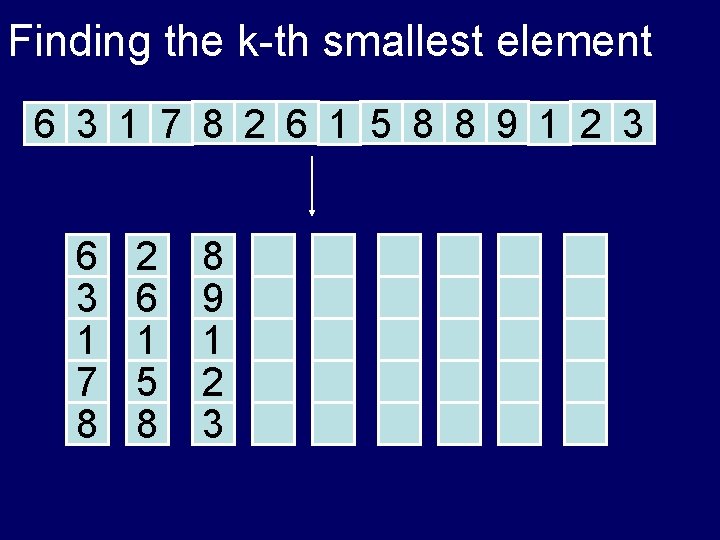
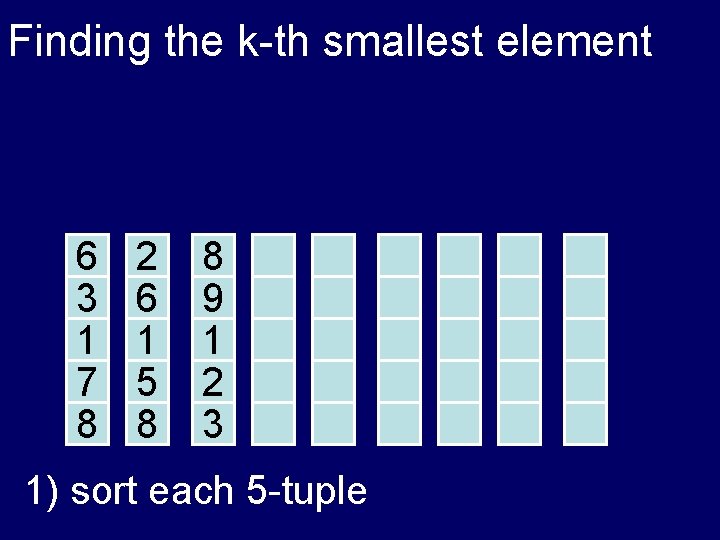
Finding the k-th smallest element 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3

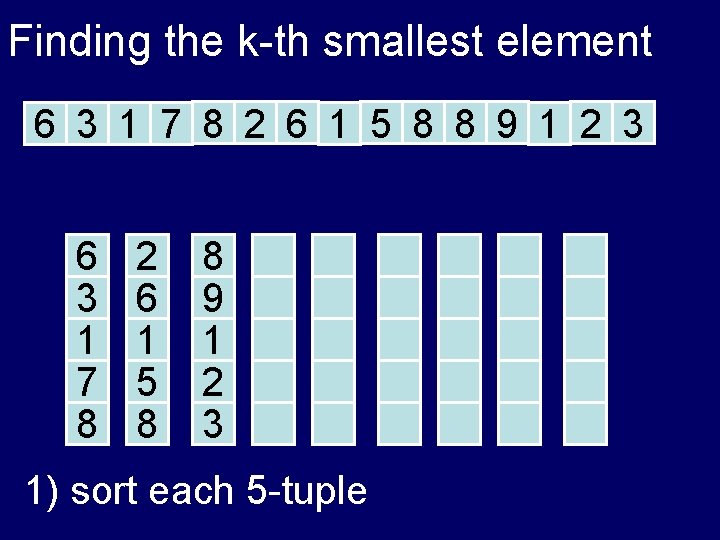
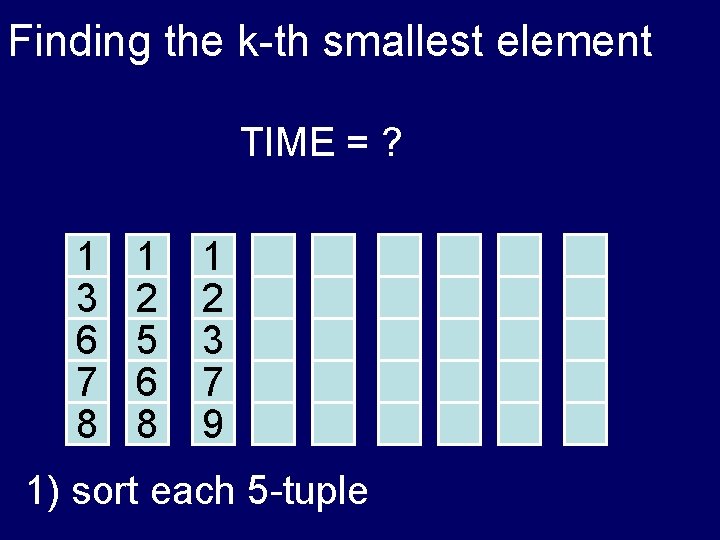
Finding the k-th smallest element 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 1) sort each 5 -tuple

Finding the k-th smallest element 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 1) sort each 5 -tuple

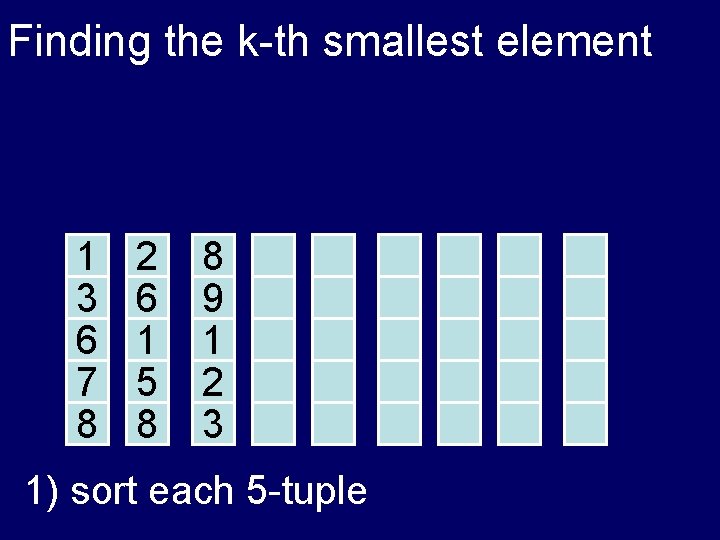
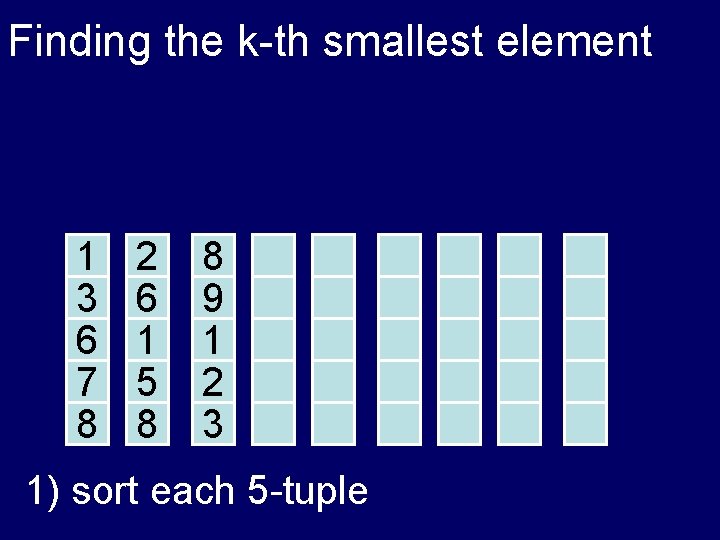
Finding the k-th smallest element 1 3 6 7 8 2 6 1 5 8 8 9 1 2 3 1) sort each 5 -tuple

Finding the k-th smallest element 1 3 6 7 8 2 6 1 5 8 8 9 1 2 3 1) sort each 5 -tuple

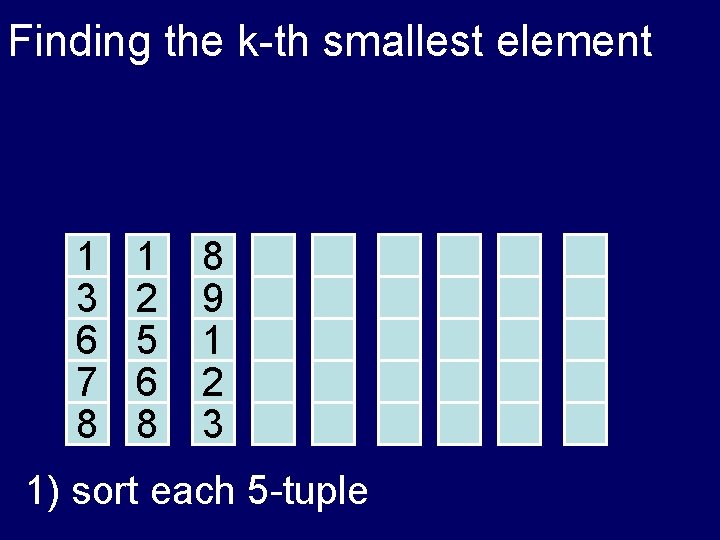
Finding the k-th smallest element 1 3 6 7 8 1 2 5 6 8 8 9 1 2 3 1) sort each 5 -tuple

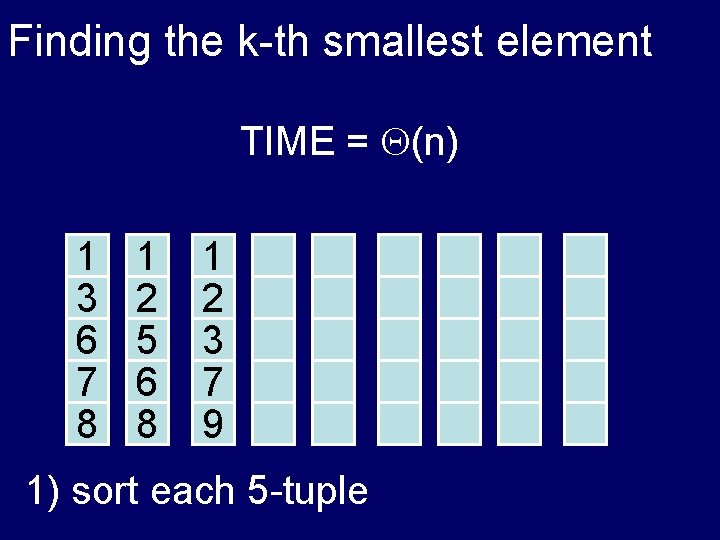
Finding the k-th smallest element TIME = ? 1 3 6 7 8 1 2 5 6 8 1 2 3 7 9 1) sort each 5 -tuple

Finding the k-th smallest element TIME = (n) 1 3 6 7 8 1 2 5 6 8 1 2 3 7 9 1) sort each 5 -tuple

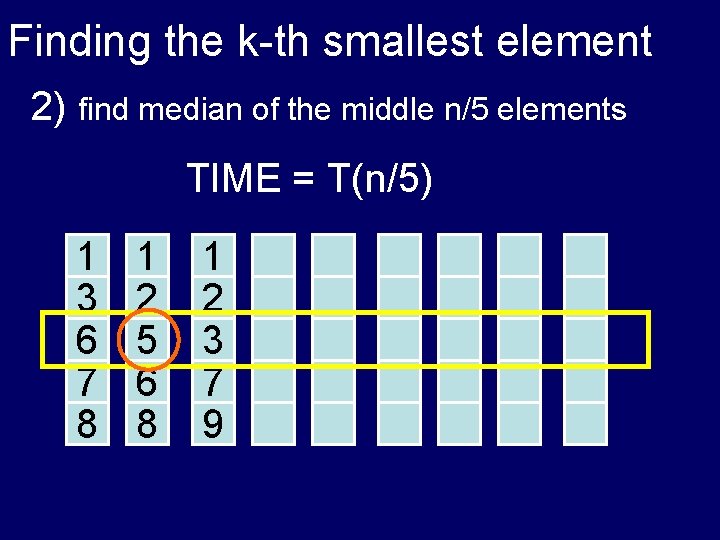
Finding the k-th smallest element 2) find median of the middle n/5 elements TIME = ? 1 3 6 7 8 1 2 5 6 8 1 2 3 7 9

Finding the k-th smallest element 2) find median of the middle n/5 elements TIME = T(n/5) 1 3 6 7 8 1 2 5 6 8 1 2 3 7 9

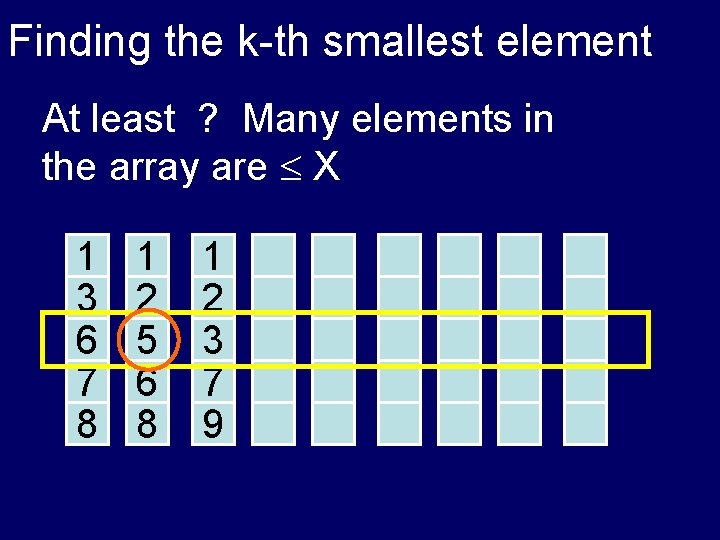
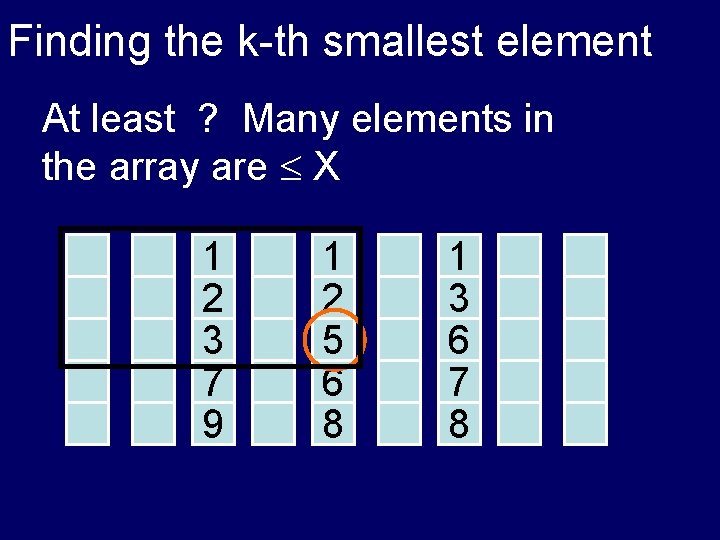
Finding the k-th smallest element At least ? Many elements in the array are X 1 3 6 7 8 1 2 5 6 8 1 2 3 7 9

Finding the k-th smallest element At least ? Many elements in the array are X 1 2 3 7 9 1 2 5 6 8 1 3 6 7 8

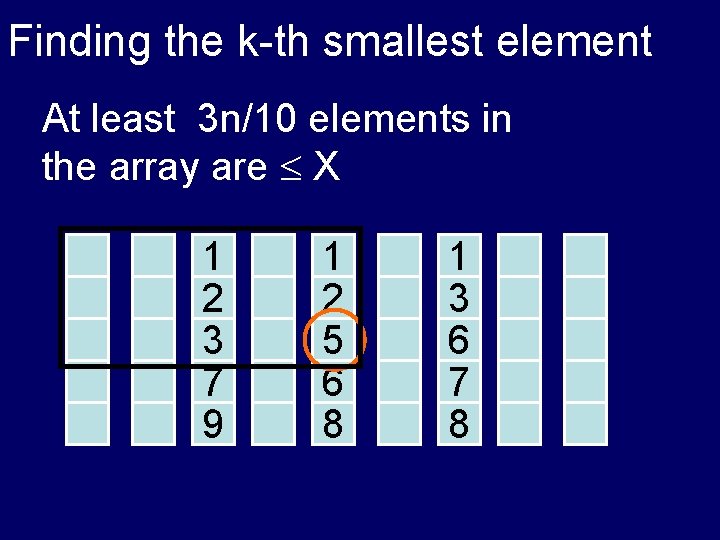
Finding the k-th smallest element At least 3 n/10 elements in the array are X 1 2 3 7 9 1 2 5 6 8 1 3 6 7 8

Finding the k-th smallest element 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 7 9 1 2 5 6 8 1 3 6 7 8 At least 3 n/10 elements in the array are X

Finding the k-th smallest element 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 X >X 3 1 2 3 2 1 1 5 8 8 9 6 7 8 6 At least 3 n/10 elements in the array are X

Finding the k-th smallest element 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 X >X 3 1 2 3 2 1 1 5 8 8 9 6 7 8 6 Recurse, time ? At least 3 n/10 elements in the array are X

Finding the k-th smallest element 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 X >X 3 1 2 3 2 1 1 5 8 8 9 6 7 8 6 Recurse, time T(7 n/10) At least 3 n/10 elements in the array are X

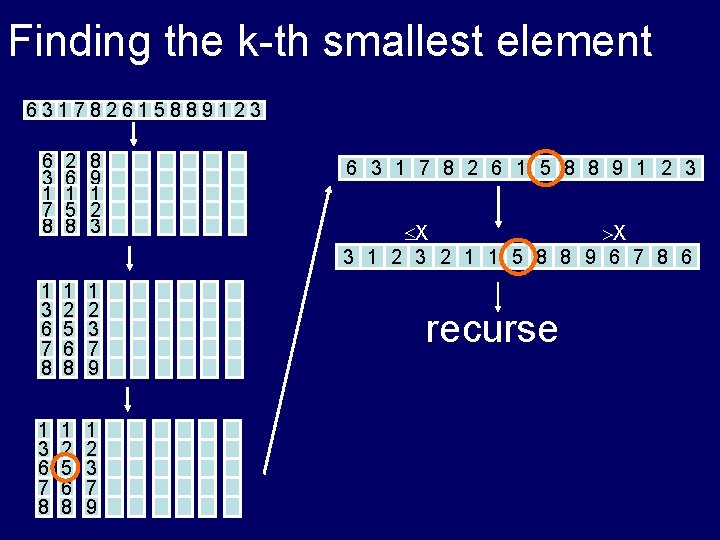
Finding the k-th smallest element 631782615889123 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 1 3 6 7 8 1 2 5 6 8 1 2 3 7 9 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 X >X 3 1 2 3 2 1 1 5 8 8 9 6 7 8 6 recurse

Finding the k-th smallest element 631782615889123 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 1 3 6 7 8 1 2 5 6 8 1 2 3 7 9 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 (n) T(n/5) (n) X >X 3 1 2 3 2 1 1 5 8 8 9 6 7 8 6 recurse T(7 n/10)

Finding the k-th smallest element T(n) T(n/5) + T(7 n/10) + O(n)

Finding the k-th smallest element T(n) T(n/5) + T(7 n/10) + O(n) T(n) d. n Induction step: T(n) T(n/5) + T(7 n/10) + O(n) d. (n/5) + d. (7 n/10) + O(n) d. n + (O(n) – dn/10) d. n

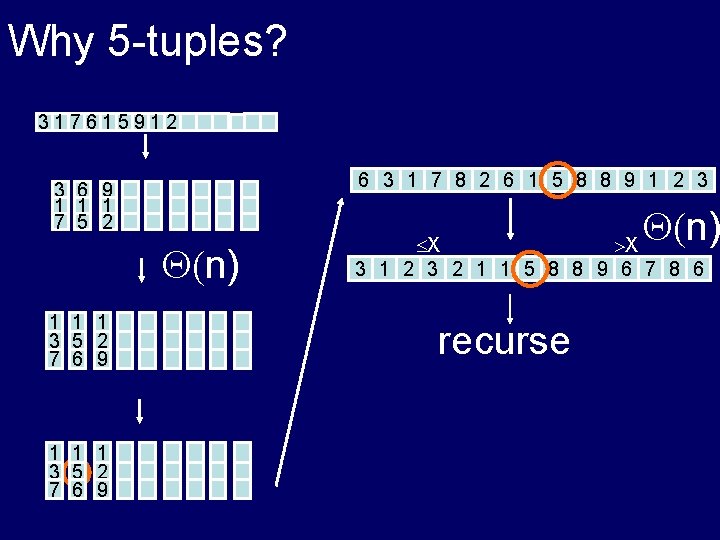
Why 5 -tuples? 317615912 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 3 6 9 1 1 1 7 5 2 (n) 1 1 1 3 5 2 7 6 9 (n) X >X 3 1 2 3 2 1 1 5 8 8 9 6 7 8 6 recurse

Why 5 -tuples? 317615912 6 3 1 7 8 2 6 1 5 8 8 9 1 2 3 3 6 9 1 1 1 7 5 2 (n) 1 1 1 3 5 2 7 6 9 T(n/3) 1 1 1 3 5 2 7 6 9 (n) X >X 3 1 2 3 2 1 1 5 8 8 9 6 7 8 6 recurse T(2 n/3)

Why 5 -tuples? T(n) = T(n/3) + T(2 n/3) + (n)

Why 5 -tuples? T(n) = T(n/3) + T(2 n/3) + (n) T(n) c. n. ln n Induction step: T(n) = T(n/3) + T(2 n/3) + (n) c. (n/3). ln (n/3) + c. (2 n/3). ln (2 n/3) + (n) c. n. ln n - c. n. ((1/3)ln 3+(2/3)ln 3/2)+ (n) c. n. ln n