Adiabatic Quantum Computing with the DWave One Bob

Adiabatic Quantum Computing with the D-Wave One Bob Lucas Federico Spedalieri Information Sciences Institute Viterbi School of Engineering USC 1

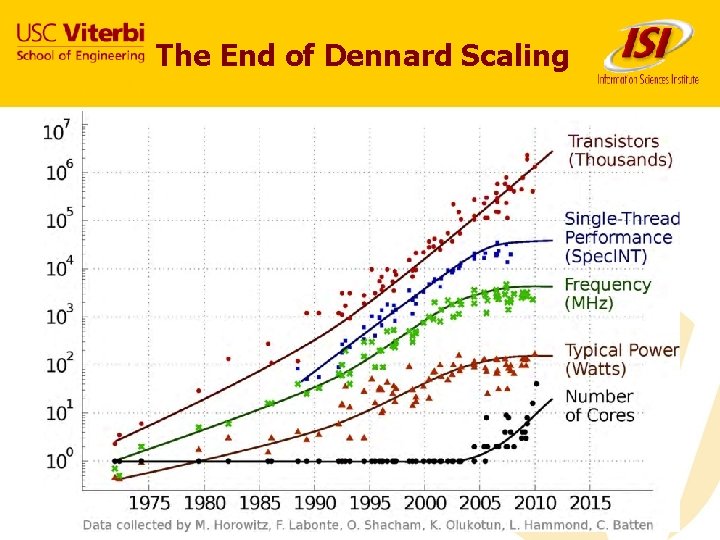
The End of Dennard Scaling

Need More Capability? Massive Scaling – ORNL Cray XK 7 Application Specific Systems D. E. Shaw Research Anton Exploit a New Phenomenon Adiabatic Quantum Processor D-Wave One

Overview • Adiabatic quantum computation • Brief description of D-Wave One • The three main thrusts of research: 1. Quantumness 2. Benchmarking 3. Applications

Adiabatic Quantum Computation E. . . Quantum computer Hamiltonian: H(t) = (1 - (t))H 0 + (t)H 1 gmin . . . E 1 E 0 0 • Prepare the computer in the ground state of H 0 • Slowly vary (t) from 0 to 1 • Read out the final state: the ground state of H 1 • Runtime associated with (gmin)-2 1

Adiabatic Quantum Optimization • Adiabatic QC is universal (can compute any function, just like circuit model) • But universality may be too much to ask for. • Consider only “classical” final Hamiltonians, i. e. : Off-diagonal (in computational basis) Diagonal (in computational basis) The final state is a classical state that minimizes the energy of H 1

Solving Ising models with AQC • Ising problem: Find • Adiabatic quantum optimization:

Overview • Adiabatic quantum computation • Brief description of D-Wave One • The three main thrusts of research: 1. Quantumness 2. Benchmarking 3. Applications

USC/ISI’s D-Wave One 128 (well, 108) qubit Rainier chip 20 m. K operating temperature 1 nano. Tesla in 3 D across processor

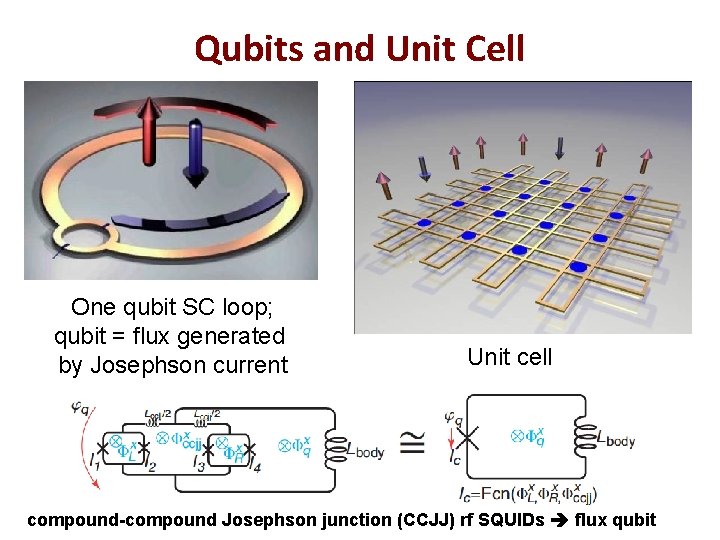
Qubits and Unit Cell One qubit SC loop; qubit = flux generated by Josephson current Unit cell compound-compound Josephson junction (CCJJ) rf SQUIDs flux qubit

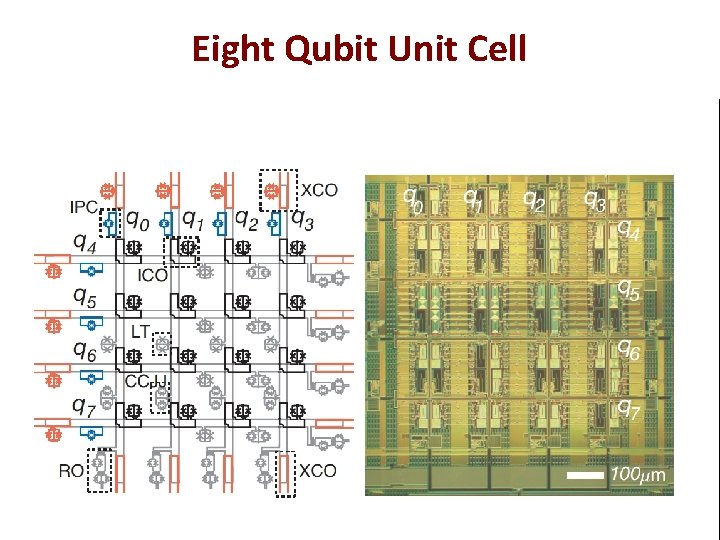
Eight Qubit Unit Cell

Tiling of Eight-Qubit Unit Cells

Adiabatic Quantum Optimization Problem: find the ground state of Use adiabatic interpolation from transverse field (Farhi et al. , 2000) Graph Embedding implemented on DW-1 via Chimera graph retains NP-hardness V. Choi (2010) 13

Program API

Overview • Adiabatic quantum computation • Brief description of D-Wave One • The three main thrusts of research: 1. Quantumness 2. Benchmarking 3. Applications

Experimental Quantum Signature (S. Boixo, T. Albash, F. S. , N. Chancellor, D. Lidar) 16

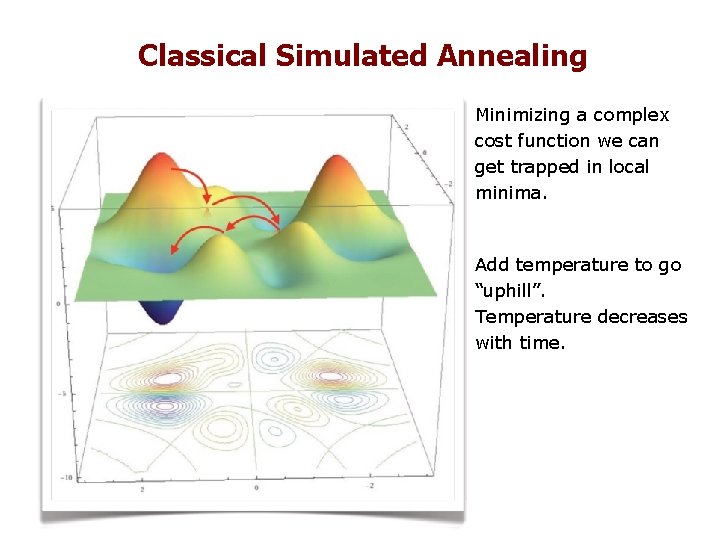
Classical Simulated Annealing Minimizing a complex cost function we can get trapped in local minima. Add temperature to go “uphill”. Temperature decreases with time.

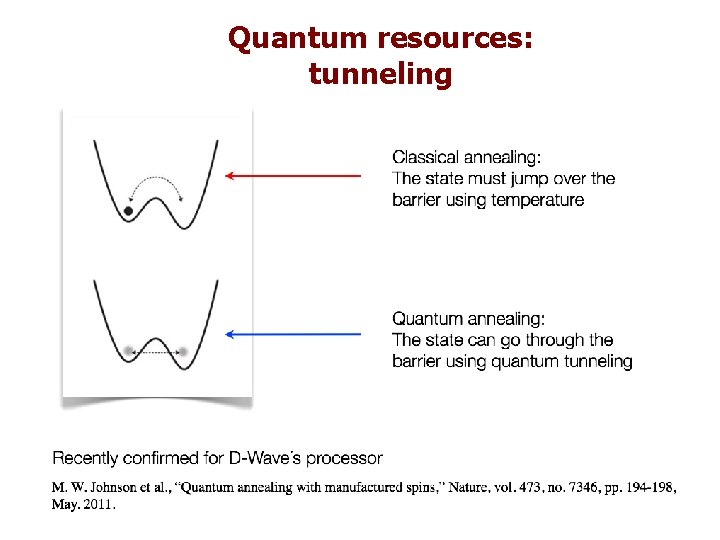
Quantum resources: tunneling

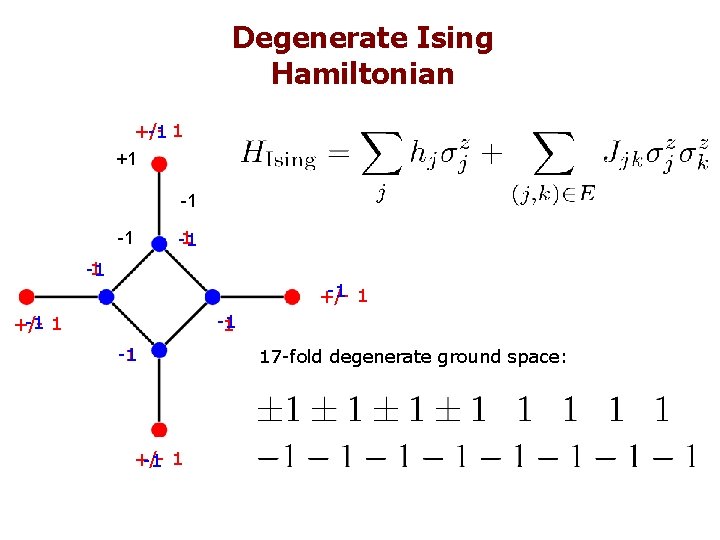
Degenerate Ising Hamiltonian +/-1 1 +1 -1 -1 1 +/-1 1 17 -fold degenerate ground space:

Classical Thermalization 20

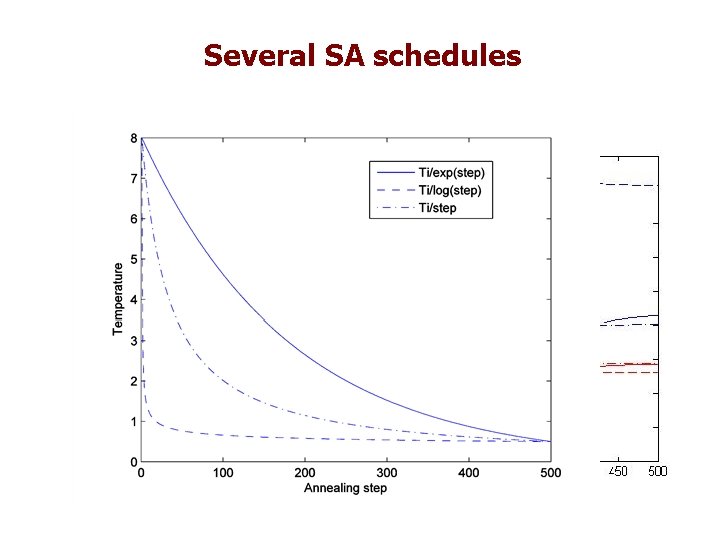
Several SA schedules

Quantum annealing 22

Quantum Annealing We want to find the ground state of an Ising Hamiltonian: Instead of “temperature” fluctuations, we use quantum fluctuations a transverse field Slowly remove the transverse field to stay on the ground state:

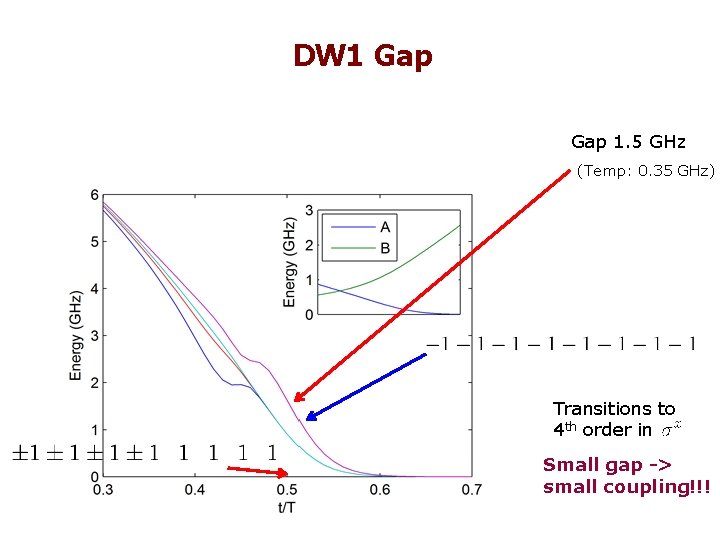
DW 1 Gap 1. 5 GHz (Temp: 0. 35 GHz) Transitions to 4 th order in Small gap -> small coupling!!!

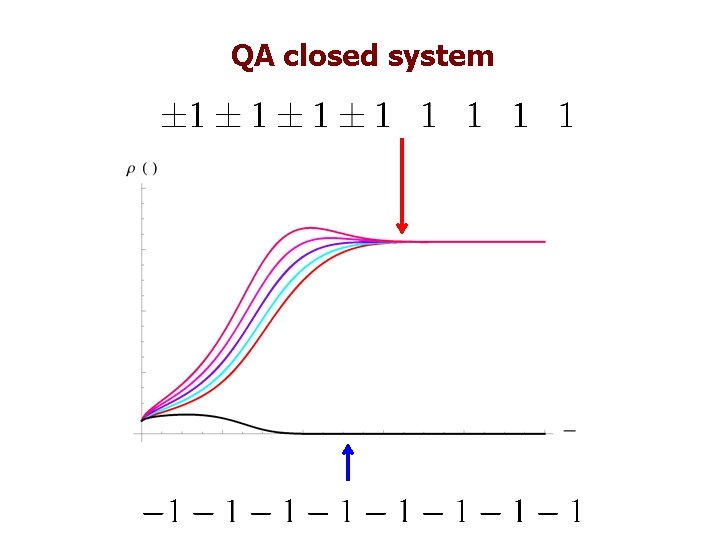
QA closed system

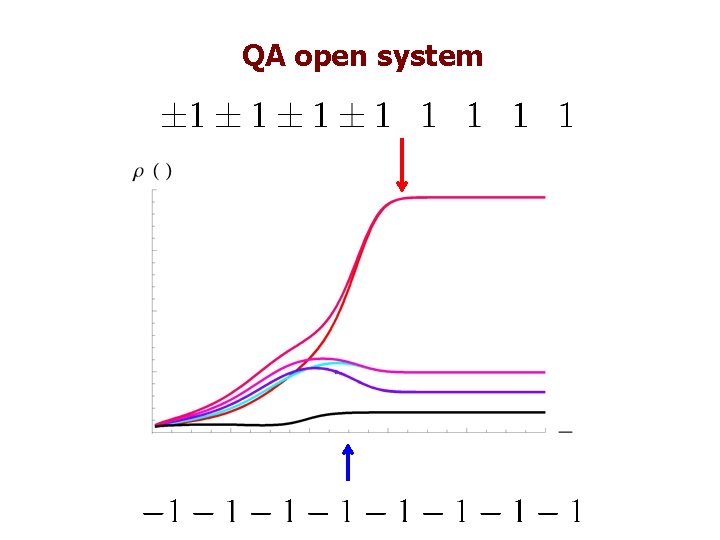
QA open system

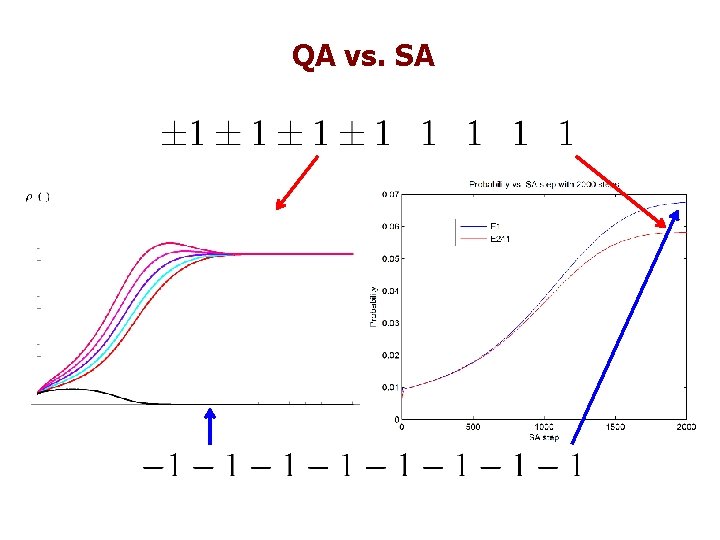
QA vs. SA

Experiments 28

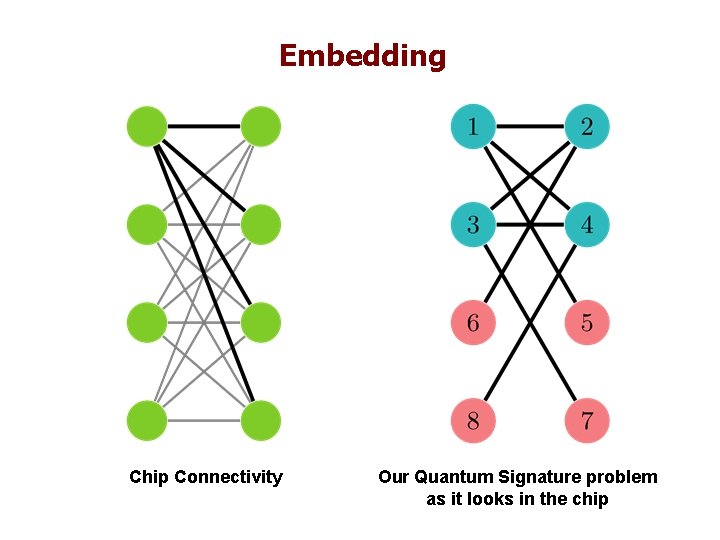
Embedding Chip Connectivity Our Quantum Signature problem as it looks in the chip

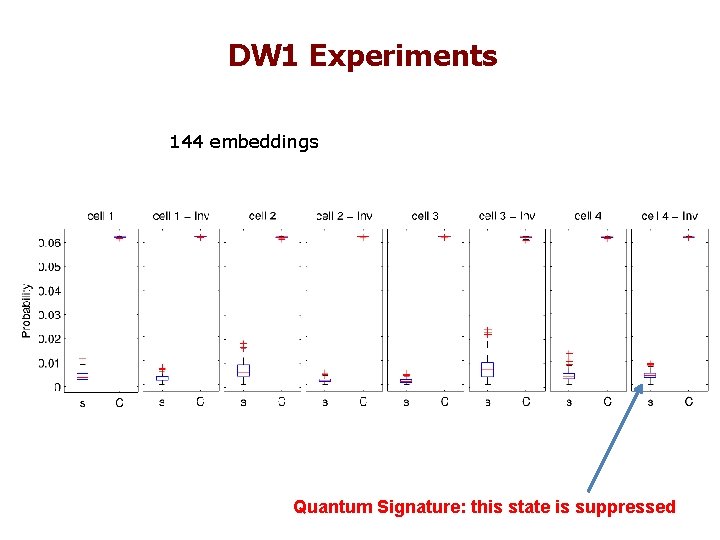
DW 1 Experiments 144 embeddings Quantum Signature: this state is suppressed

Entanglement 31

Entanglement: a definition • Separable states • It is a classical mixture of product states • It can be constructed locally • Entangled states 32

ENTANGLEMENT IN DW 2 • Even numerically, determining if a state is entangled is NP-hard • How can we experimentally show entanglement? 1. Measure the complete density matrix of the system Quantum State Tomography • • • Requires a large number of measurements (exponential in the number of qubits) The reconstructed density matrix may not be physical (not PSD) For DW 2, these measurements are not even possible 2. Measure an observable that distinguishes entangled states Entanglement Witnesses • • For every entangled state there is an entanglement witness Measuring the expectation of Z can prove entanglement But to find Z we need to know the state (or be very lucky) The measurements required will likely not be available in DW 2 Separable States

Magnetic susceptibilities in DW 2 • Use a weakly coupled probe to measure • Compute the magnetic susceptibilities as • Use perturbation theory (and some assumptions) to write

Separability criteria • Apply PPTSE separability criteria to this general state • All separable states have a PPTSE for any k • Search for PPTSE can be cast as a semidefinite program • Produces a hierarchy of separability tests • If state is entangled, dual SDP computes an entanglement witness

Separability criteria with partial information • Some properties of this approach: 1. If the test fails the state may still be entangled 1. We can use a dual approach that checks if a state satisfying the linear constraints is separable (also a SDP) 2. If both tests fail, we need to go to higher k 3. All entangled states will be detected for some k 1. Going beyond k=2 may be tricky (the size of the SDP gets too big) 2. In theory, this is the best you can do with partial information: if you could run the tests for all k, this approach will eventually prove that all states satisfying the linear constraints are entangled or that there is one such state that is separable 36

Overview • Adiabatic quantum computation • Brief description of D-Wave One • The three main thrusts of research: 1. Quantumness 2. Benchmarking 3. Applications

Benchmarking 38

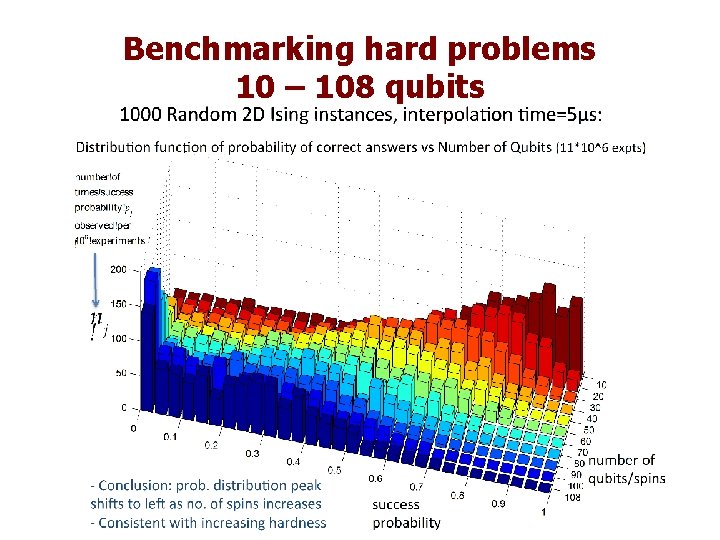
Benchmarking hard problems 10 – 108 qubits

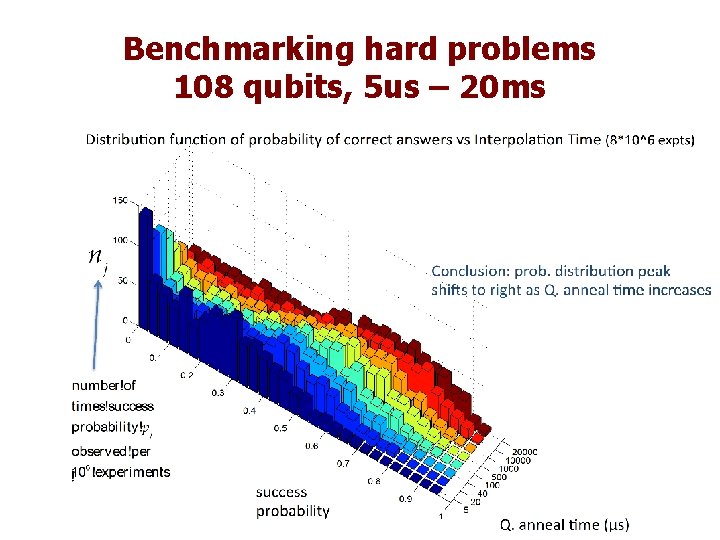
Benchmarking hard problems 108 qubits, 5 us – 20 ms

Classical repetition cost r

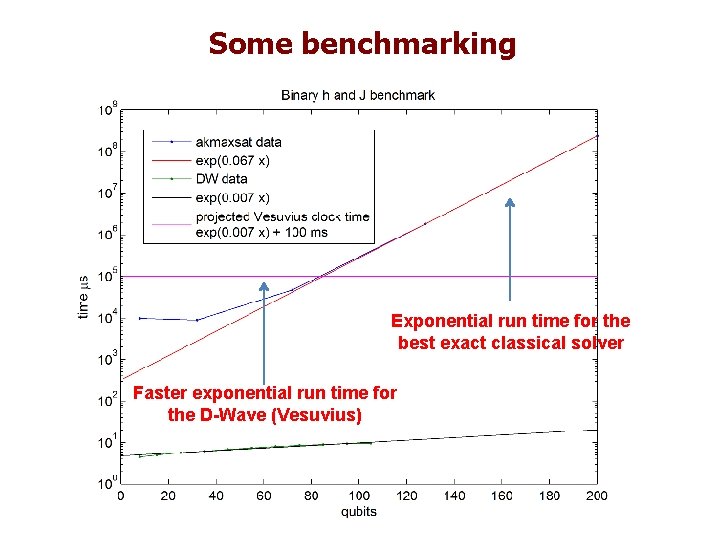
Some benchmarking Exponential run time for the best exact classical solver Faster exponential run time for the D-Wave (Vesuvius)

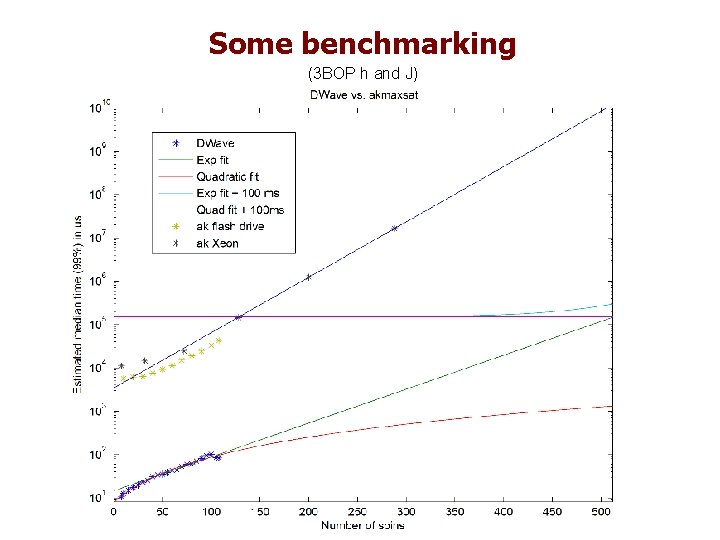
Some benchmarking (3 BOP h and J)

Overview • Adiabatic quantum computation • Brief description of D-Wave One • The three main thrusts of research: 1. Quantumness 2. Benchmarking 3. Applications

Some NP-complete problems and their applications The problem addressed by quantum annealing is NP-Complete Problem Application Traveling salesman Logistics, vehicle routing Minimum Steiner tree Circuit layout, network design Graph coloring Scheduling, register allocation MAX-CLIQUE Social networks, bioinformatics QUBO Machine learning (H. Neven, Google) Integer Linear Programming Natural language processing Sub-graph isomorphism Cheminformatics, drug discovery Job shop scheduling Manufacturing Motion planning Robotics MAX-2 SAT Artificial intelligence

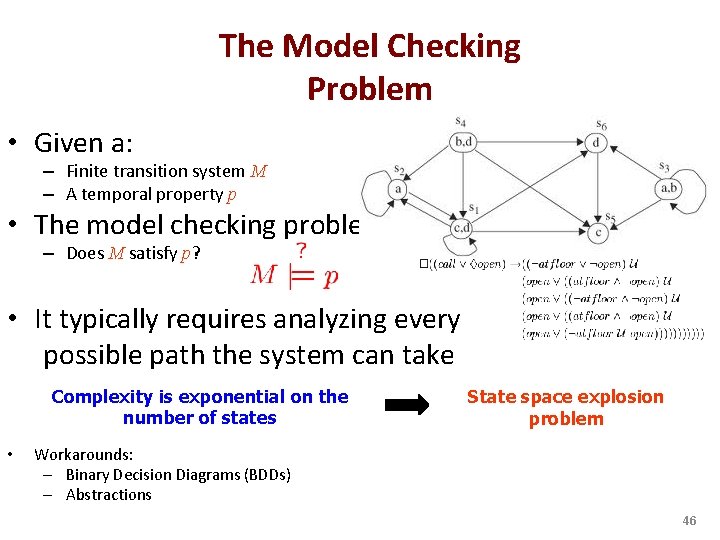
The Model Checking Problem • Given a: – Finite transition system M – A temporal property p • The model checking problem: – Does M satisfy p? • It typically requires analyzing every possible path the system can take Complexity is exponential on the number of states • State space explosion problem Workarounds: – Binary Decision Diagrams (BDDs) – Abstractions 46

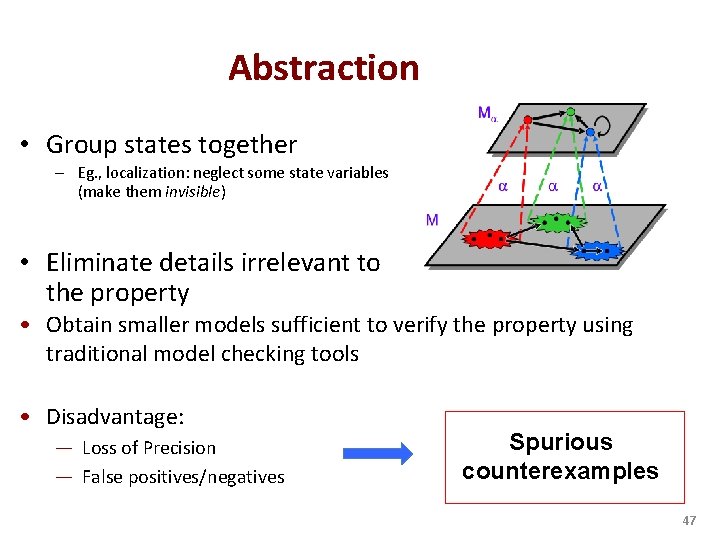
Abstraction • Group states together – Eg. , localization: neglect some state variables (make them invisible) • Eliminate details irrelevant to the property • Obtain smaller models sufficient to verify the property using traditional model checking tools • Disadvantage: — Loss of Precision — False positives/negatives Spurious counterexamples 47

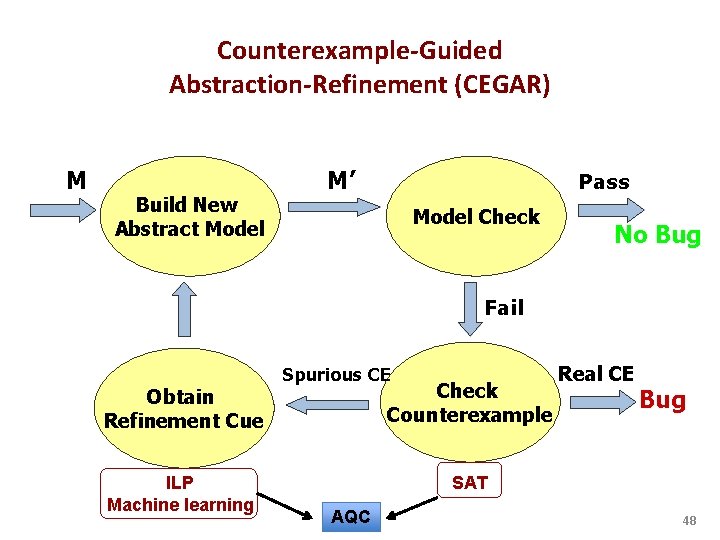
Counterexample-Guided Abstraction-Refinement (CEGAR) M Build New Abstract Model M’ Pass Model Check No Bug Fail Obtain Refinement Cue ILP Machine learning Spurious CE Check Counterexample Real CE Bug SAT AQC 48

Summary • DW 1 is a programmable superconducting quantum adiabatic processor • It solves a particular type of combinatorial optimization problem • We have investigated the quantum nature of the device • We chose a problem for which classical thermalization and quantum annealing predict different statistics • Experiments agree with quantum annealing prediction suggesting quantum annealing is surprisingly robust against noise • Working on an experimental test for entanglement • Benchmarks show promising scaling when compared with classical solvers • Currently working to bridge the gap between the device and real applications (non-trivial issues to be addressed)