ADDITIONAL NOTE CHAP 2 POWER SYSTEM REPRESENTATION 1

ADDITIONAL NOTE CHAP 2 POWER SYSTEM REPRESENTATION 1

ONE-LINE DIAGRAMS � In solving a power system network, it is often involve a single-phase and three-phase equivalent circuit. � For the three-phase system, that may consist of three lines and a neutral return when drawing a diagram of the circuit. � The complicated diagrams of the circuits can be simplified and called as a single-line or one-line diagram. � One-line diagram is a simplified single-phase circuit diagram of a balanced three-phase electric power system as shown in Figure 1. R Y B 3 -phase system One-line system Figure 1: 3 -phase system to one-line system 2

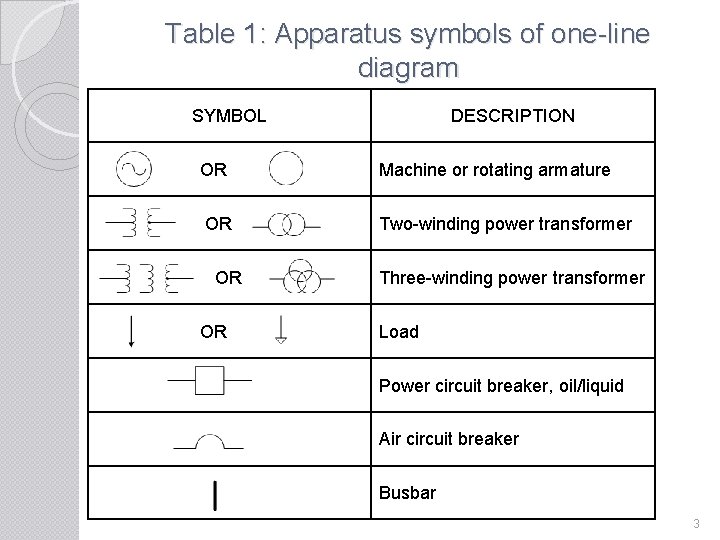
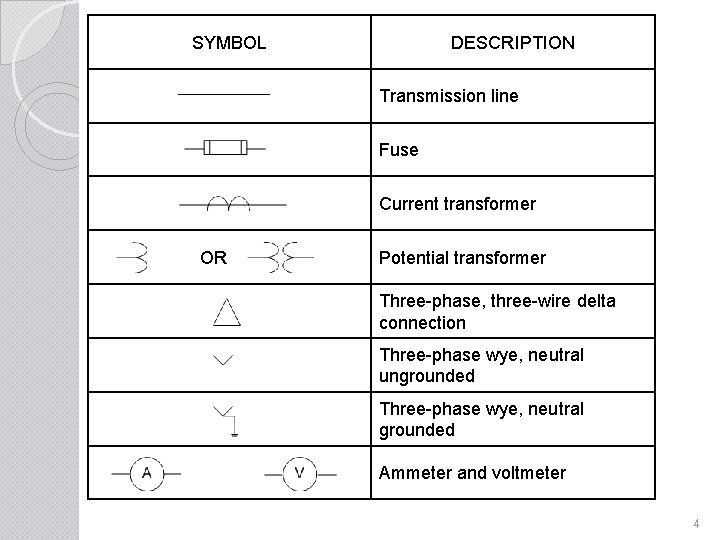
Table 1: Apparatus symbols of one-line diagram SYMBOL DESCRIPTION OR Machine or rotating armature OR Two-winding power transformer OR Three-winding power transformer OR Load Power circuit breaker, oil/liquid Air circuit breaker Busbar 3

SYMBOL DESCRIPTION Transmission line Fuse Current transformer OR Potential transformer Three-phase, three-wire delta connection Three-phase wye, neutral ungrounded Three-phase wye, neutral grounded Ammeter and voltmeter 4

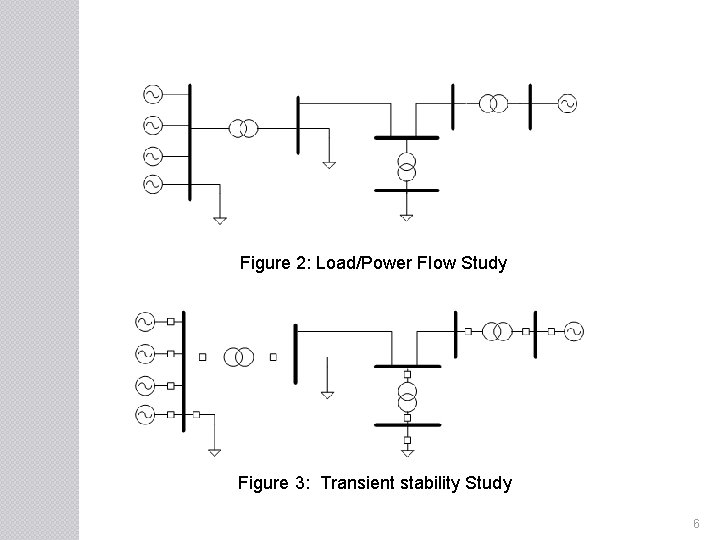
ONE-LINE DIAGRAMS �The information on a one-line diagram is vary according to the problem at hand the practice of the particular company preparing the diagram. �The one-line diagram has its largest application in power flow and transient stability studies. 5

Figure 2: Load/Power Flow Study Figure 3: Transient stability Study 6

ONE-LINE DIAGRAMS �The advantages of the one-line diagram are: ◦ Simplicity. ◦ One phase represents all three phase of the balanced system. ◦ The equivalent circuits of the components are placed by their standard symbols. ◦ The completion of the circuit through the neutral is omitted. 7

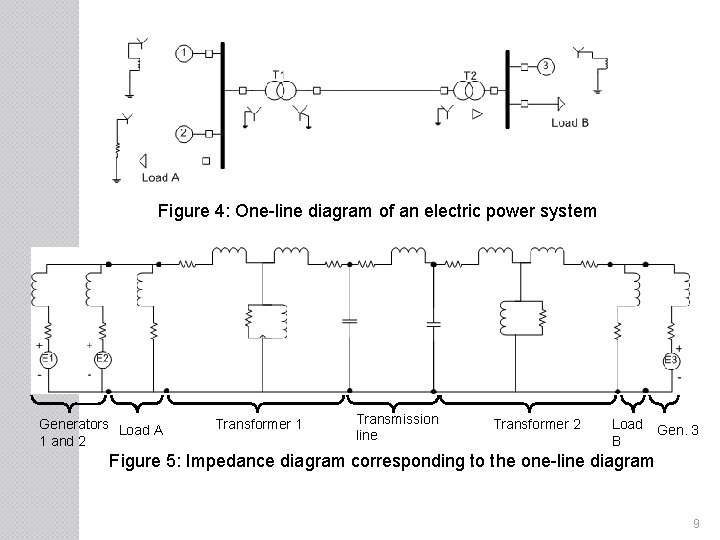
IMPEDANCE AND REACTANCE DIAGRAMS �The impedance (Z= R + j. X) diagram is converted from one-line diagram showing the equivalent circuit of each component of the system. �It is needed in order to calculate the performance of a system under load conditions (Load flow studies) or upon the occurrence of a short circuit (fault analysis studies). �Reactance (j. X) diagram is further simplified from impedance diagram by omitting all static loads, all resistances, the magnetizing current of each transformer, and the capacitance of the transmission line. �It is apply to fault calculations only, and not to load flow studies. �The impedance and reactance diagrams 8

Figure 4: One-line diagram of an electric power system Generators Load A 1 and 2 Transformer 1 Transmission line Transformer 2 Load Gen. 3 B Figure 5: Impedance diagram corresponding to the one-line diagram 9

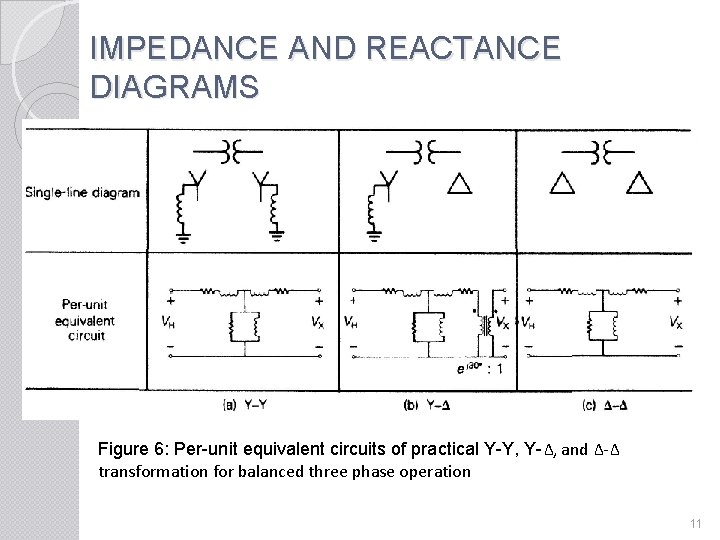
IMPEDANCE AND REACTANCE DIAGRAMS � A generator can be represented by a voltage source in series with an inductive reactance. The internal resistance of the generator is negligible compared to the reactance. � The load are inductive. � The transformer core is ideal, and the transformer may be represented by an reactance. � The transmission line is a medium-length line and can be denoted by T circuit. An alternative representation, such as a π circuit, is equally applicable. � The wye-delta connected transformer T 2 may be replaced y an equivalent wye-wye connected transformer (via a delta to wye transformation) so that the impedance diagram may be drawn on a per-phase basis. 10

IMPEDANCE AND REACTANCE DIAGRAMS Figure 6: Per-unit equivalent circuits of practical Y-Y, Y-Δ, and Δ-Δ transformation for balanced three phase operation 11

IMPEDANCE AND REACTANCE DIAGRAMS Generators 1 and 2 Transformer 1 Transmission line Transformer 2 Gen. 3 Figure 7: Reactance diagram corresponding to the one-line diagram �The reactance diagram is drawn by neglecting all resistance, the static loads, and the capacitance of the transmission line. 12

13

PER-UNIT REPRESENTATION � The common quantities used in power system analysis are voltage (k. V), current (k. A), voltamperes (k. VA or MVA), and impedance (Ω). � It is very cumbersome to convert to a different voltage level in a power system having two or more voltage levels. � Per-unit representation is introduced such that the various physical quantities are expressed as a decimal fraction or multiples of base quantities and defined as: � In other word, the per-unit value of any quantity is the ratio of the quantity to its base expressed as a decimal and denoted by p. u. 14

PER-UNIT REPRESENTATION �The advantages of Per-Unit Quantities are: ◦ The apparatus of the same general type of p. u. volt drops and losses are in the same order, regardless of size. ◦ The use of in three-phase calculations is reduced. ◦ By the choice of appropriate voltage bases, the solution of networks containing several transformers is facilitated. ◦ Per-unit quantities more readily to digital computation. 15

PER-UNIT REPRESENTATION �Formulas relate the various quantities for single-phase system: �Formulas relate the various quantities for three-phase system: 16

SUMMARY OF THREE-PHASE CIRCUIT RELATIONSHIP �A three-phase circuit may be connected either in wye or in delta. �In a balanced three-phase circuit, the phase and the line values of the current, power, and voltage are related as follows: �Wye connection: ◦ ILN = ILL ◦ VLN = VLL /√ 3 ◦ P = √ 3 VLLILL cosθ �Delta connection: ◦ ILN = ILL /√ 3 ◦ VLN = VLL ◦ P = √ 3 VLLILL cosθ 17

SUMMARY OF THREE-PHASE CIRCUIT RELATIONSHIP �The delta and wye impedances are related by: ◦ Zwye = 1/3 Zdelta �For both types of connections, the apparent and reactive powers are: ◦ VA = √ 3 VLLILL and ◦ Q = √ 3 VLLILL sinθ �From the above, it is clear that the phrase angle may be obtained as: ◦ tan θ = Q/P 18

PER-UNIT CONVERSION STEP, 1ϕ STEP 1: Choose a 1ϕ VA base for the entire system, Sbase, 1ϕ STEP 2: Choose a voltage base for each different voltage level, Vbase. Voltage base are related by transformer turns ratio. Voltage are line to neutral. STEP 3: Calculate the impedance base, Zbase. STEP 4: Calculate the current base, 19

PER-UNIT CONVERSION STEP, 3ϕ STEP 1: Choose a 3ϕ VA base for the entire system, Sbase, 3ϕ STEP 2: Choose a voltage base for each different voltage level, Vbase. Voltage are line to line. STEP 3: Calculate the impedance base, Zbase. STEP 4: Calculate the current base, Ibase. STEP 5: Calculate actual values to per- 20

NOTICES AND RULES �Regardless of whether delta or wye: ◦ Choose base voltages in same ratio as the nominal line-line voltages ◦ Choose base VA same on both sides �Result is the per-phase equivalent circuit in per-unit system has no ideal transformer in equivalent circuit 21

EXAMPLE A power system consists of one synchronous generator and one synchronous motor connected by two transformers and a transmission line. Create a per-phase, per-unit equivalent circuit of this power system using a base apparent power of 100 MVA and a base line voltage of the generator G 1 of 13. 8 k. V. Given that: G 1 ratings: 100 MVA, 13. 8 k. V, R= 0. 1 pu, Xs =0. 9 pu; T 1 ratings: 100 MVA, 13. 8/110 k. V, R= 0. 01 pu, Xs=0. 05 pu; T 2 ratings: 50 MVA, 120/14. 4 k. V, R= 0. 01 pu, Xs = 0. 05 pu; M ratings: 50 MVA, 13. 8 k. V, R = 0. 1 pu, Xs = 1. 1 pu; L 1 impedance: R = 15 Ω, X = 75 Ω 22

STEP 1 & STEP 2 To create a per-phase, per-unit equivalent circuit, we need first to calculate the impedances of each component in the power system in per-unit to the system base. The system base apparent power is Sbase = 100 MVA everywhere in the power system. The base voltage in the three regions will vary as the voltage ratios of the transformers that delineate the regions. These base voltages are: 23

STEP 3 The corresponding base impedances in each region are: 24

STEP 4 The impedances of G 1 and T 1 are specified in per-unit on a base of 13. 8 k. V and 100 MVA, which is the same as the system base in Region 1. Therefore, the per-unit resistances and reactances of these components on the system base are unchanged: RG 1, pu = 0. 1 per unit XG 1, pu = 0. 9 per unit RT 1, pu = 0. 01 per unit X T 1, pu = 0. 05 per unit 25

STEP 4 (continue) There is a transmission line in Region 2 of the power system. The impedance of the line is specified in ohms, and the base impedance in that region is 121Ω Therefore, the per-unit resistance and reactance of the transmission line are: 26

STEP 4 (continue) The impedance of T 2 is specified in perunit on a base of 14. 4 k. V and 50 MVA in Region 3. Therefore, the per-unit resistances and reactances of this component on the system base are: 27

STEP 4 (continue) The impedance of M 2 is specified in perunit on a base of 13. 8 k. V and 50 MVA in Region 3. Therefore, the per-unit resistances and reactances of this component on the system base are: 28

�Therefore, the per-phase, per-unit equivalent circuit of this power system is shown: 29

EXERCISE 1. A 345 k. V transmission line has a series impedance of (4+j 60)Ω and a shunt admittance of j 2 x 10 -3 S. using 100 MVA and the line voltage as base values, calculate the per-unit impedance and per-unit admittance of the line. 30

EXERCISE 2. A three-phase, wye connected system is rated at 50 MVA and 120 k. V. Express 40, 000 k. VA of three-phase apparent power as a per-unit value referred to: a) the three-phase system k. VA as base. b) the per-phase system k. VA as base. 31

EXERCISE 3. A three-phase, wye-connected, 6. 25 k. VA, 220 V synchronous generator has a reactance of 8. 4 Ω per phase. Using the rates k. VA and voltage as base values, determine the per-unit reactance. Then refer this per-unit value to a 230 V, 7. 5 k. VA base. 32

EXERCISE 4. A three-phase, 13 k. V transmission line delivers 8 MVA of load. The perphase impedance of the line is (0. 01+j 0. 05) pu, referred to a 13 k. V, 8 MVA base. What is the voltage drop across the line? 33

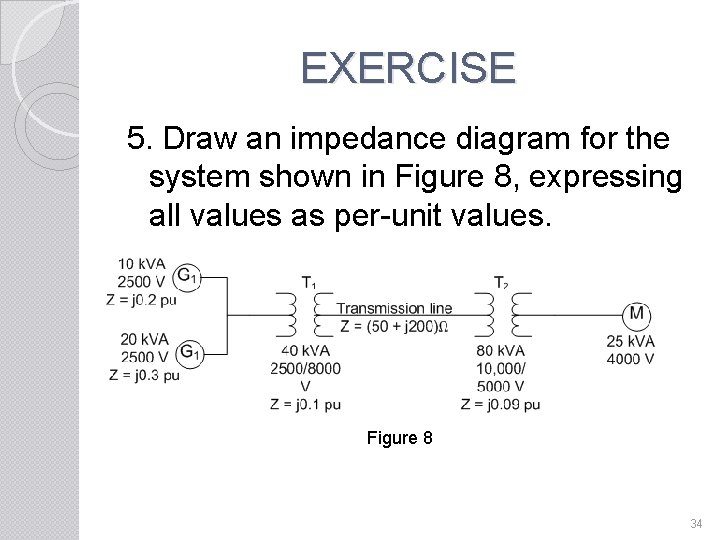
EXERCISE 5. Draw an impedance diagram for the system shown in Figure 8, expressing all values as per-unit values. Figure 8 34