Addition of vectors i Triangle Rule For vectors

Addition of vectors (i) Triangle Rule [For vectors with a common point] C B A

(ii) Parallelogram Rule [for vectors with same initial point] D C B A

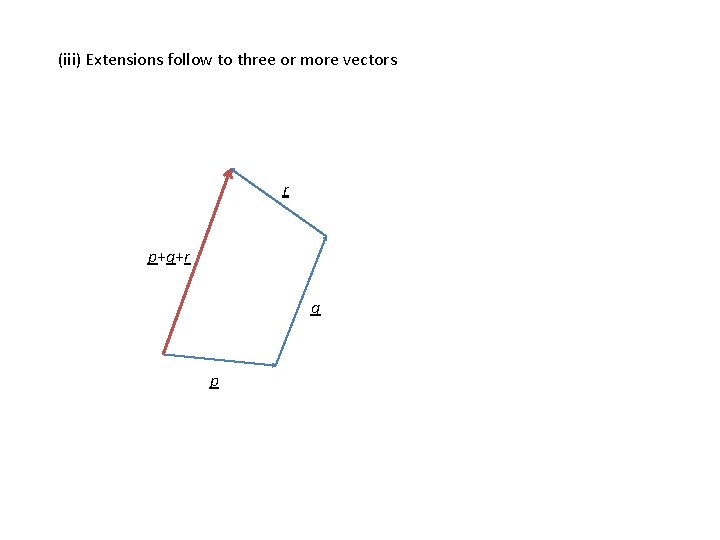
(iii) Extensions follow to three or more vectors r p+q+r q p

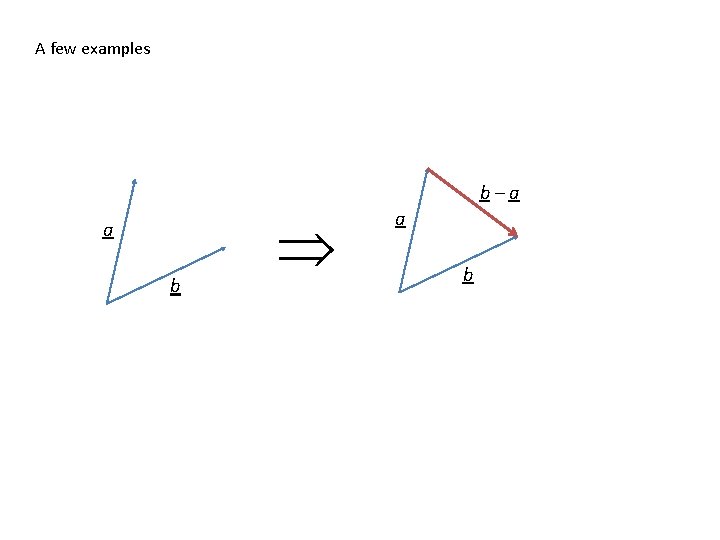
Subtraction First we need to understand what is meant by the vector – a a –a a and – a are vectors of the same magnitude, are parallel, but act in opposite senses.

A few examples b–a a b

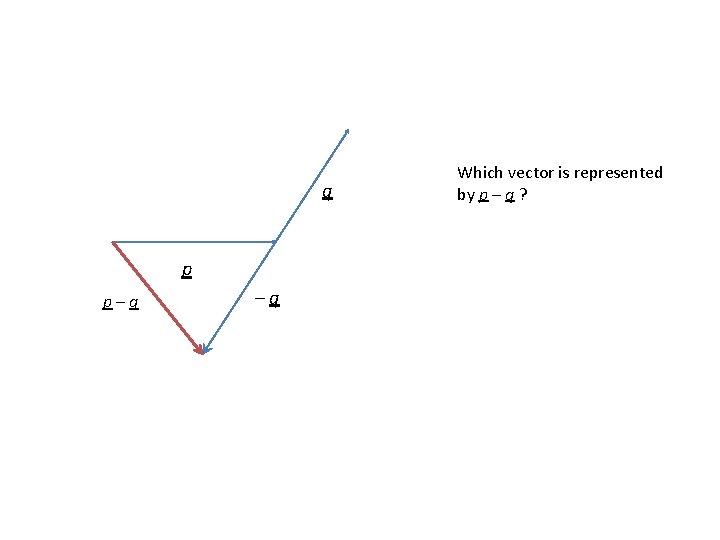
q p p–q –q Which vector is represented by p – q ?

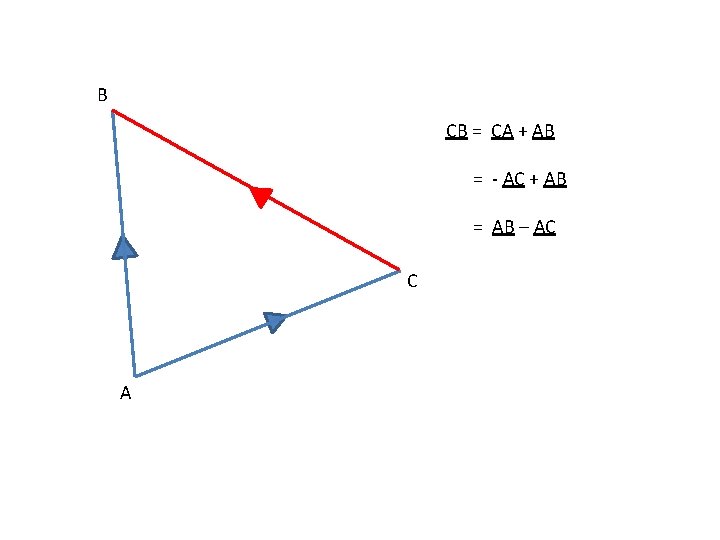
B CB = CA + AB = - AC + AB = AB – AC C A

Position Vectors Relative to a fixed point O [origin] the position of a Point P in space is uniquely determined by OP P p O OP is a position vector of a point P. We usually associate p with OP

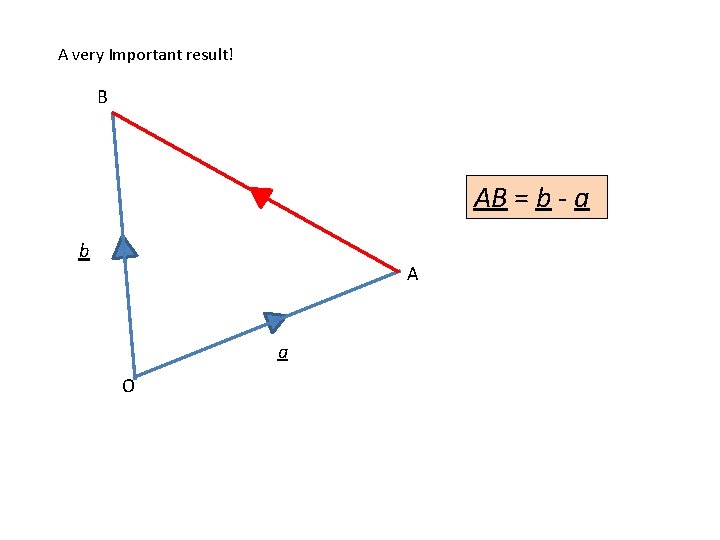
A very Important result! B AB = b - a b A a O

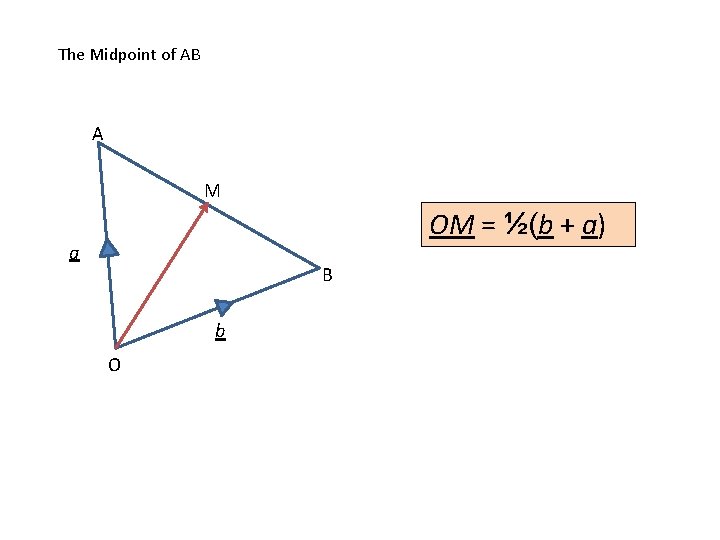
The Midpoint of AB A M OM = ½(b + a) a B b O

An Important technique To establish or express the co-linearity of three points [Lie in a straight line] Choose any two line segments, AB, AC or BC. For the points to be co-linear AB, AC or BC must lie in the same direction Example B Given OA = p, OC = q and OB = 2 p – q , show that A, B and A C are co-linear. BC = BO + OC AB = AO + OB C = – (2 p – q) + q = – p + (2 p – q) = =p–q = – 2(p – q ) = – 2 AB 2 q – 2 p O AB &BC are parallel (even though in opposite directions) and have a common point B Hence A , B and C are co-linear.

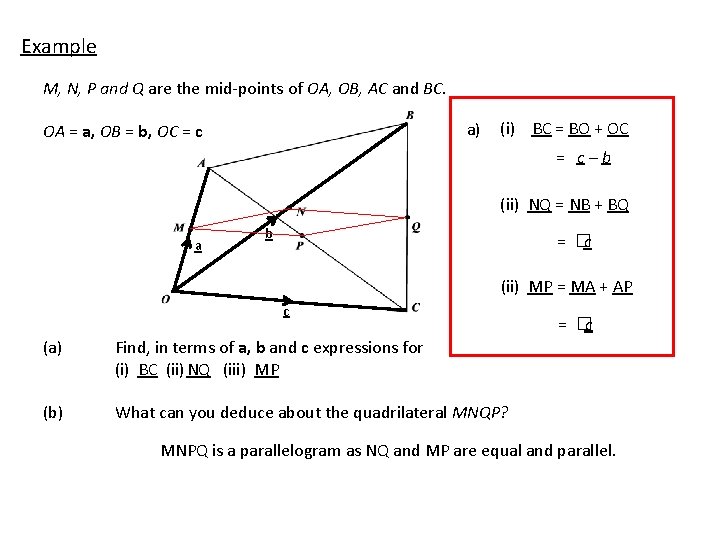
Example M, N, P and Q are the mid-points of OA, OB, AC and BC. a) OA = a, OB = b, OC = c (i) BC = BO + OC = c–b (ii) NQ = NB + BQ a b = �c (ii) MP = MA + AP c (a) Find, in terms of a, b and c expressions for (i) BC (ii) NQ (iii) MP (b) What can you deduce about the quadrilateral MNQP? = �c MNPQ is a parallelogram as NQ and MP are equal and parallel.

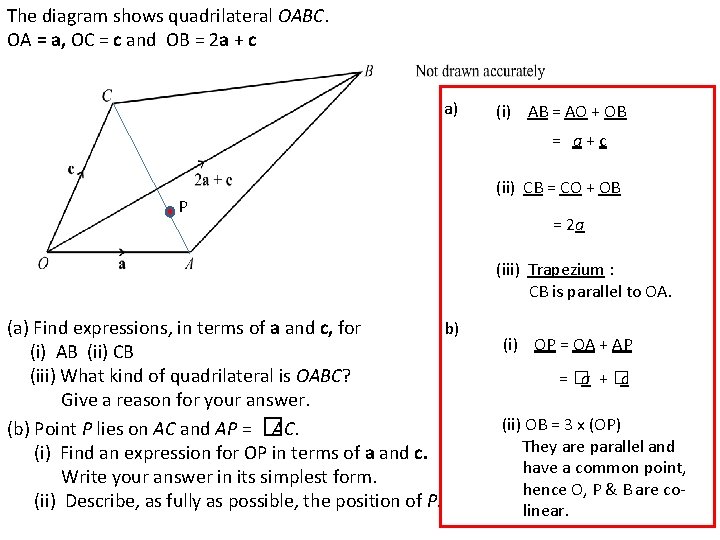
The diagram shows quadrilateral OABC. OA = a, OC = c and OB = 2 a + c a) (i) AB = AO + OB = a+c P (ii) CB = CO + OB = 2 a (iii) Trapezium : CB is parallel to OA. b) (a) Find expressions, in terms of a and c, for (i) AB (ii) CB (iii) What kind of quadrilateral is OABC? Give a reason for your answer. (b) Point P lies on AC and AP = � AC. (i) Find an expression for OP in terms of a and c. Write your answer in its simplest form. (ii) Describe, as fully as possible, the position of P. (i) OP = OA + AP = �a + �c (ii) OB = 3 x (OP) They are parallel and have a common point, hence O, P & B are colinear.

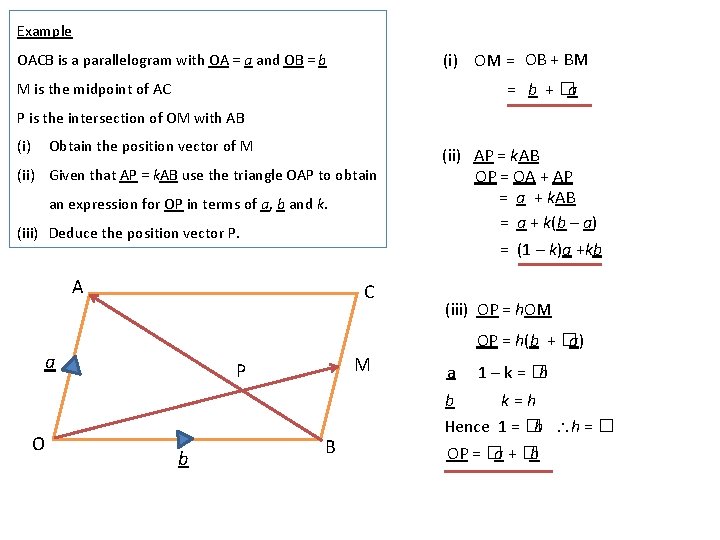
Example OACB is a parallelogram with OA = a and OB = b M is the midpoint of AC P is the intersection of OM with AB (i) Obtain the position vector of M (ii) Given that AP = k. AB use the triangle OAP to obtain an expression for OP in terms of a, b and k. (iii) Deduce the position vector P.

Example (i) OM = OB + BM OACB is a parallelogram with OA = a and OB = b + �a M is the midpoint of AC P is the intersection of OM with AB (i) Obtain the position vector of M (ii) Given that AP = k. AB use the triangle OAP to obtain an expression for OP in terms of a, b and k. (iii) Deduce the position vector P. A C (iii) OP = h. OM OP = h(b + �a) a O (ii) AP = k. AB OP = OA + AP = a + k. AB = a + k(b – a) = (1 – k)a +kb M P b B a 1 – k = �h b k=h Hence 1 = �h h = � OP = �a + �b