Adding Subtracting Polynomials Lesson 10 1 Learning Goal

Adding & Subtracting Polynomials Lesson 10. 1

Learning Goal 1 (HS. N-RN. B 3 and HS. A-SSE. A. 1): The student will be able to use properties of rational and irrational numbers to write, simplify, and interpret expressions based on contextual situations. 4 3 2 In addition to level 3. 0 and above and beyond what was taught in class, the student may: · Make connection with other concepts in math · Make connection with other content areas. The student will be able to use properties of rational and irrational numbers to write, simplify, and interpret expressions on contextual situations. - justify the sums and products of rational and irrational numbers -interpret expressions within the context of a problem The student will be able to use properties of rational and irrational numbers to write and simplify expressions based on contextual situations. -identify parts of an expression as related to the context and to each part 1 0 With help Even with from the help, the teacher, the student has no success partial with real success with number real number expressions.

Polynomial: Poly: Many Form: nomial: terms axk Where k is a non-negative integer. This is a polynomial in one variable. k is the degree of ax. ax alone has a degree of 1 The constant “a” has a degree of 0.

Degree: the degree of a polynomial is the largest degree of its terms. Standard form: terms are written in descending order from the largest to the smallest degree. Coefficient: the integer in front of the variable. How many you have of each variable. If no number, you have one.

Put this in standard form. -4 x 2 + 3 x 3 + 2 3 x 3 – 4 x 2 + 2 Name the coefficients and degree. 2 x 3 + (-1)x 2 + 5 -5 x 2 + 10 x - 3 Coefficients: 2, -1 Degree: 3 Coefficients: -5, 10 Degree: 2

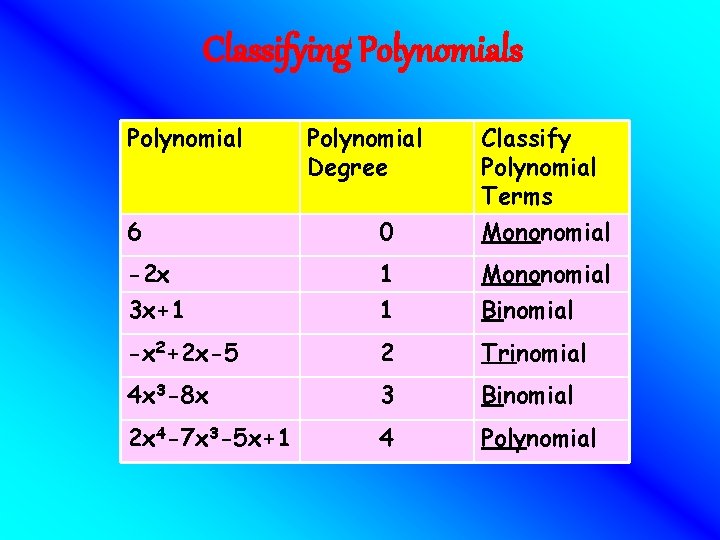
Classifying Polynomials Polynomial Degree Classify Polynomial Terms 6 0 Mononomial -2 x 1 Mononomial 3 x+1 1 Binomial -x 2+2 x-5 2 Trinomial 4 x 3 -8 x 3 Binomial 2 x 4 -7 x 3 -5 x+1 4 Polynomial

Adding Polynomials: add like terms! You add the coefficients, not the variables! Horizontal format: (2 x 2+x-5) + (x 2+x+6) = 2 x 2+x+x-5+6 =3 x 2+2 x+1 remove ( )

Vertical format: line up like terms and add. (2 x 2+x-5) + (x 2+x+6) 2 x 2+x-5 + x 2+x+6 3 x 2+2 x+1 remove ( ) and line up like terms.

Subtracting polynomials: use either vertical or horizontal format. ***Remember to change the signs of every term in the second polynomial when you remove the ( )! Vertical format: (8 x 4 -3 x 2 -11 x-3) – (-13 x 4 -3 x 2+2 x-17) 8 x 4 - 3 x 2 - 11 x - 3 13 x 4+3 x 2 -2 x+17 (combine after changing signs) 21 x 4 -13 x+14

Horizontal format: (8 x 4 -3 x 2 -11 x-3) – (-13 x 4 -3 x 2+2 x-17) Remove ( ) changing the signs in the second polynomial. You are adding the opposites! 8 x 4 -3 x 2 -11 x-3 + 13 x 4+3 x 2 -2 x+17 now combine like terms ( 21 x 4 -13 x+14 Classify this by degree and terms. 4, trinomial )

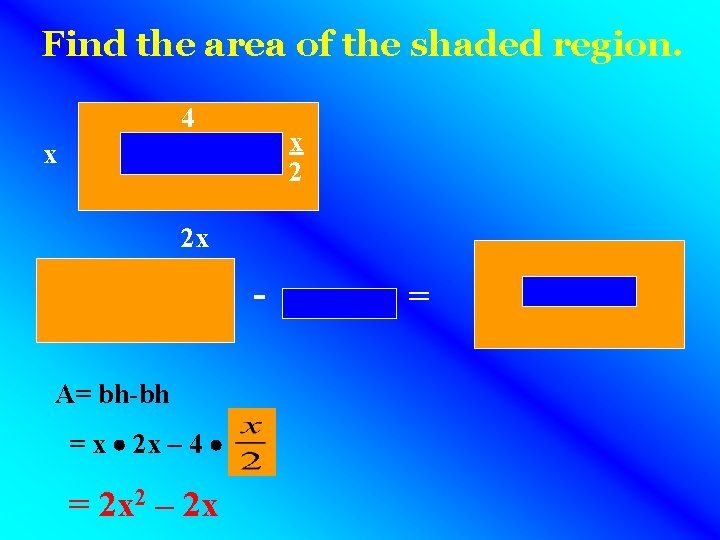
Find the area of the shaded region. 4 x 2 x A= bh-bh = x 2 x – 4 = 2 x 2 – 2 x =