ADDING INTEGERS SAME SIGNS SAME signs keep the



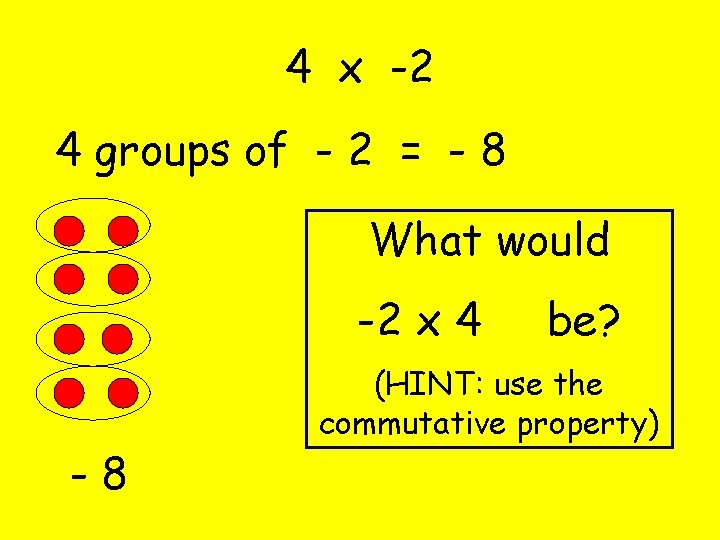
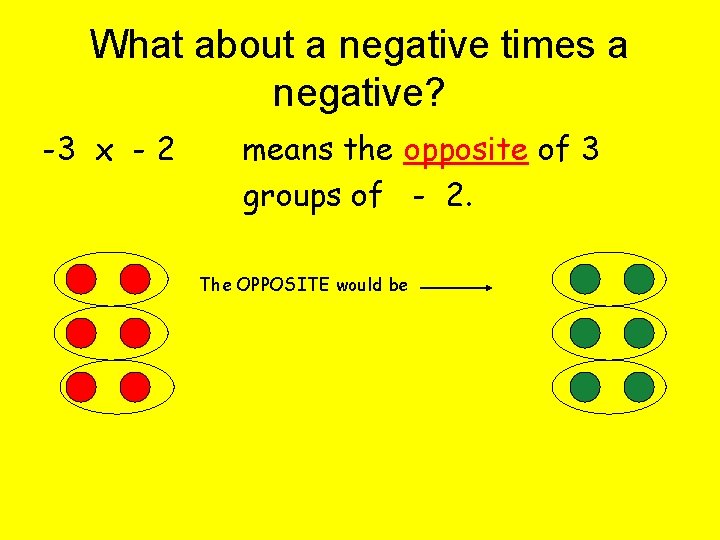





- Slides: 17

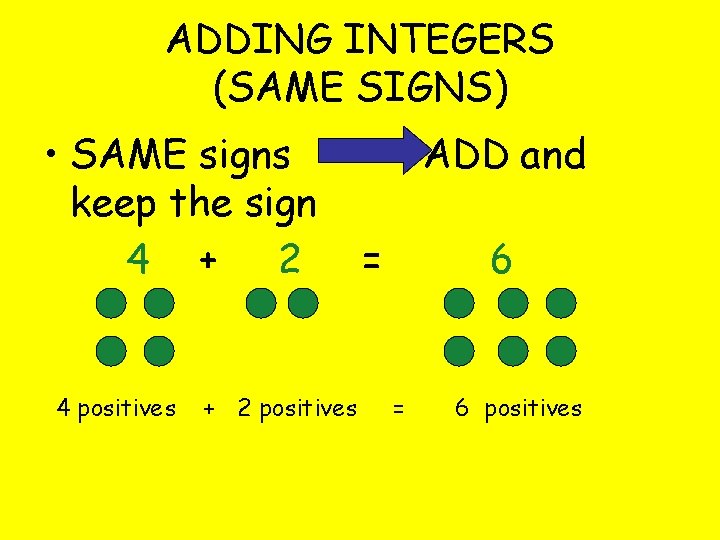
ADDING INTEGERS (SAME SIGNS) • SAME signs keep the sign 4 + 2 4 positives + 2 positives ADD and = 6 positives

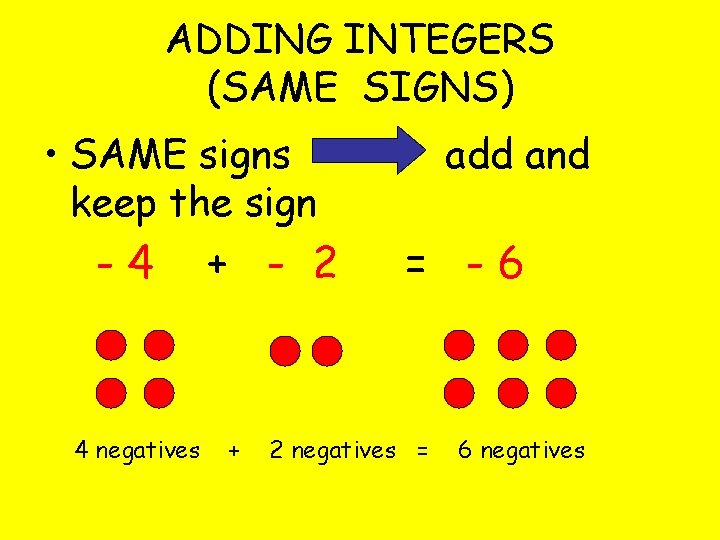
ADDING INTEGERS (SAME SIGNS) • SAME signs keep the sign -4 4 negatives + - 2 + add and = -6 2 negatives = 6 negatives

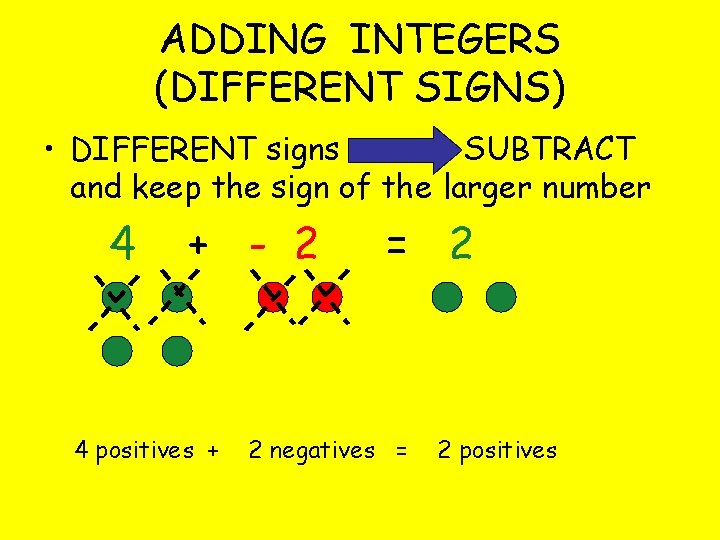
ADDING INTEGERS (DIFFERENT SIGNS) • DIFFERENT signs SUBTRACT and keep the sign of the larger number 4 + - 2 4 positives + = 2 2 negatives = 2 positives

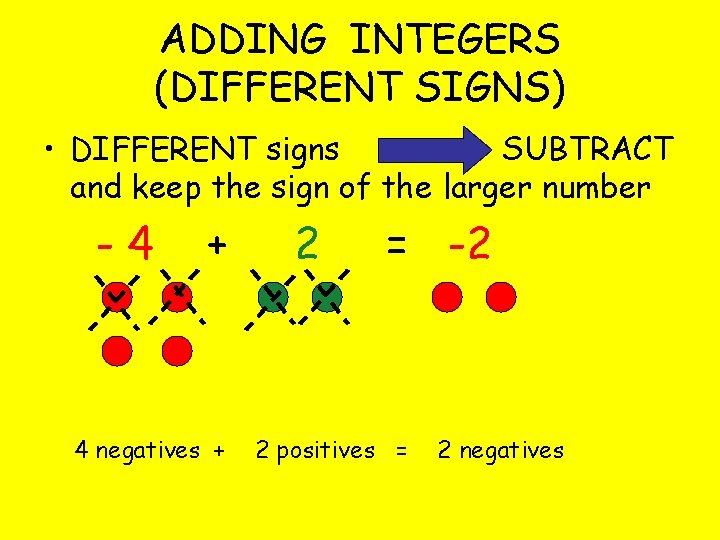
ADDING INTEGERS (DIFFERENT SIGNS) • DIFFERENT signs SUBTRACT and keep the sign of the larger number -4 + 4 negatives + 2 = -2 2 positives = 2 negatives

SUBTRACTING INTEGERS (KFC & follow Rules for addition) Problem 8 - 10 KFC follow addition rules 8 + - 10 K – keep the first number F – flip the subtraction to an addition sign C – change the second number to its opposite ****then****** FOLLOW RULES FOR ADDITION!!!!

Steps 1. Is it an addition or subtraction problem? A. Addition (go to step 2) B. Subtraction (go to step 3) 2. Addition – are the signs the same? A. Yes – add and keep the sign B. No – subtract and keep the sign of the larger number 3. Subtraction – KFC –Keep the first number; Flip to an addition problem; Change the last number to its opposite – then go back to step 2

MULTIPLYING INTEGERS Multiplying is REPEATED ADDITION Commutative Property of Multiplication - the order in which numbers are multiplied does not matter axb=bxa

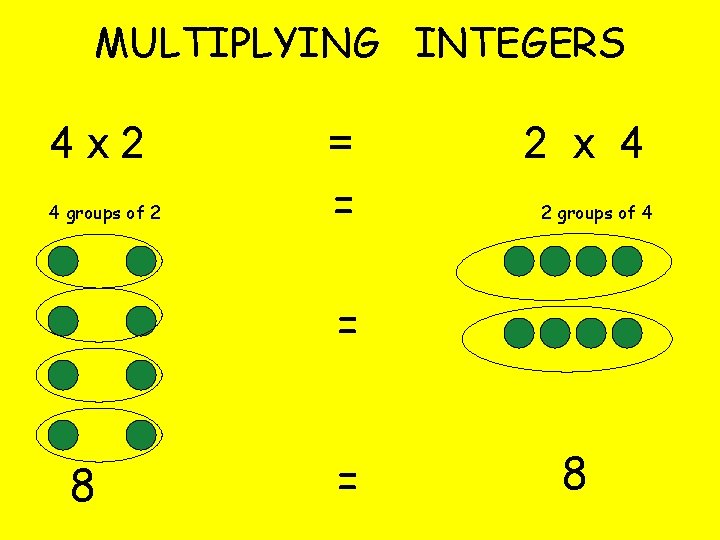
MULTIPLYING INTEGERS 4 x 2 4 groups of 2 = = 2 x 4 2 groups of 4 = 8
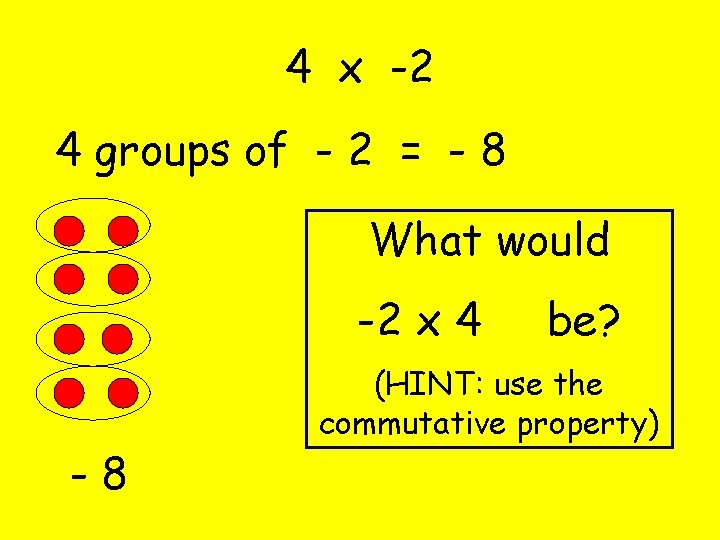
4 x -2 4 groups of - 2 = - 8 What would -2 x 4 -8 be? (HINT: use the commutative property)

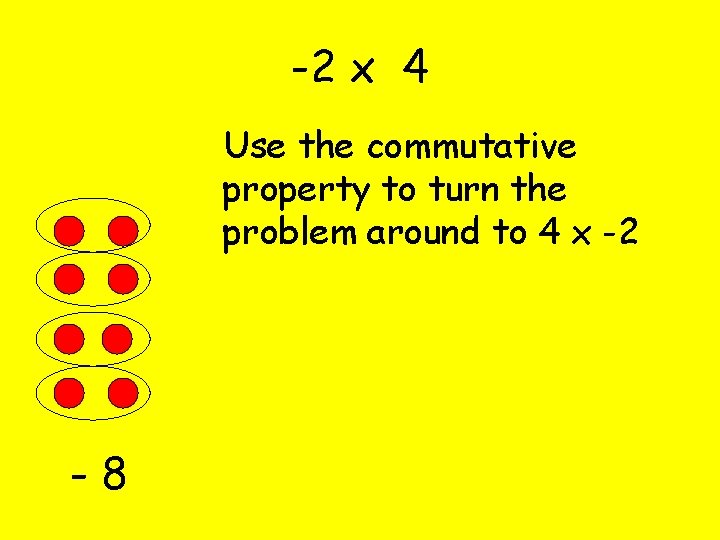
-2 x 4 Use the commutative property to turn the problem around to 4 x -2 -8

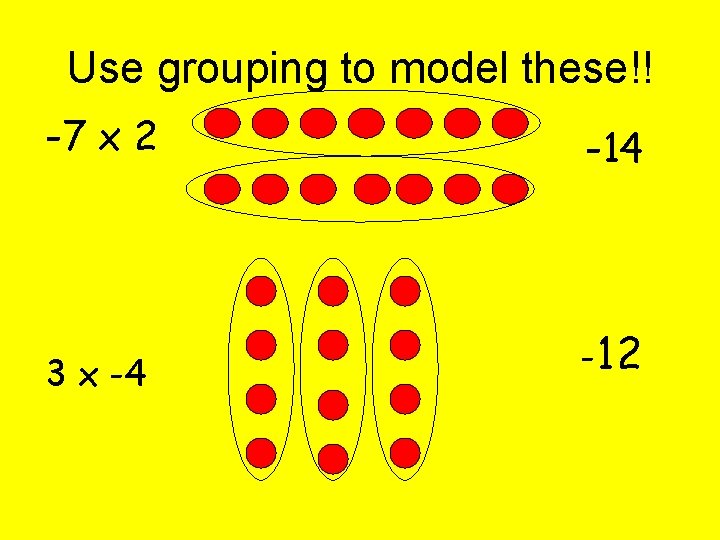
Use grouping to model these!! -7 x 2 -14 3 x -4 -12
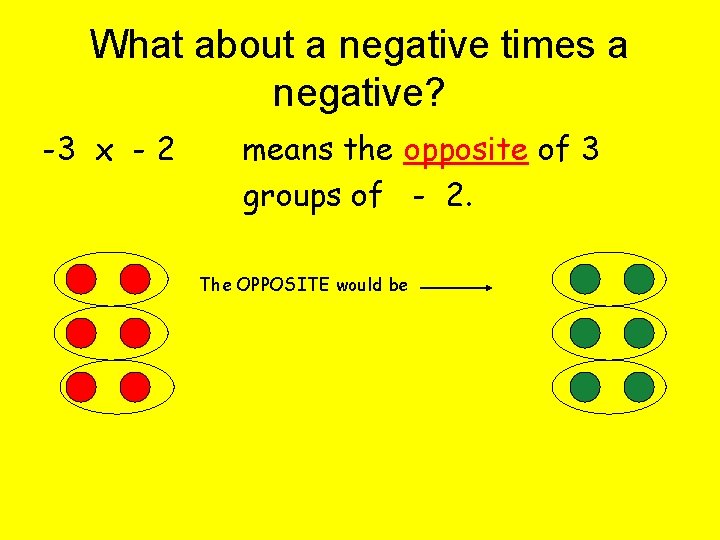
What about a negative times a negative? -3 x - 2 means the opposite of 3 groups of - 2. The OPPOSITE would be

Another way to look at negative times a negative using the Distributive Property…. . -5 (- 6 + 6) -5 ( -6 + 6 ) -5 (0) (-5)(-6) + (-5)( 6) =0 So we know that -5 (-6 + 6) equals 0 ? + -30 =0 For the problem to equal zero, the negative times a negative must equal a positive!

Multiplying Integers Rules • If the signs are the same (+ x + or - x -); multiply and the answer is positive • If the signs are different ( + x – or - x +); multiply and the answer is negative

Dividing Integers Division is the inverse operation of multiplication. 4 x 2=8 inverse 4 x (– 2 )= (-8) inverse 8 ÷ 2 =4 (-8) ÷ (-2) = 4

Dividing Integers (-5) x 3 =(-15) inverse 2 x (-3) = (-6) inverse (-15) ÷ 3 = -5 (-6) ÷ (-3) = 2

Rules for Division Same as Multiplication: • If the signs are the same (+ x + or - x -); multiply and the answer is positive • If the signs are different ( + x – or - x +); multiply and the answer is negative