Adding and Subtracting Scientific Notation Adding and Subtracting

Adding and Subtracting Scientific Notation

Adding and Subtracting… n The important thing to remember about adding or subtracting is that the exponents must be the same! n If the exponents are not the same then it is necessary to change one of the numbers so that both numbers have the same exponential value.

Part 1 Adding in Scientific Notation

Adding… n The general format for adding is as follows… n (N x 10 x) + (M x 10 x) = (N + M) x 10 x n The first step, if necessary, is to change one of the numbers so that both numbers have the same exponential value.

Adding… n Secondly, add the N and M numbers together and express as an answer. n The final step is to multiply the result by the 10 x. n (It may be necessary to put the resulting answer into proper scientific notation. )

Adding With the Same Exponent n (3. 45 x 103) + (6. 11 x 103) n 3. 45 + 6. 11 = 9. 56 n 9. 56 x 103

Adding With Different Exponents n (4. 12 x 106) + (3. 94 x 104) n (412 x 104) + (3. 94 x 104) n 412 + 3. 94 = 415. 94 n 415. 94 x 104 n Express n in proper form: 4. 15 x 106 If you had adjusted the exponents originally to the 6 th power, you would end up with the same result

Now it’s your turn. n (6. 89 x 104) + (9. 24 x 105)

Part 2 Subtracting in Scientific Notation

Subtracting… n The general form for subtracting is as follows… n (N x 10 x) – (M x 10 x) = (N – M) x 10 x n The first step, if necessary is to change one of the numbers so that both numbers have the same exponential value. (Just like adding).

Subtracting… n Secondly, subtract the M number from the N number and express as an answer. n The final step is to multiply the result by the 10 x. n (It may be necessary to put the resulting answer into proper scientific notation. )

Subtracting With the Same Exponent n (8. 96 x 107) – (3. 41 x 107) n 8. 96 – 3. 41 = 5. 55 n 5. 55 x 107

Subtracting With Different Exponents n (4. 23 x 103) – (9. 56 x 102) n (4. 23 x 103) – (0. 956 x 103) n 4. 23 – 0. 956 = 3. 274 n 3. 274 x 103 n If you had adjusted the exponents originally to the 2 nd power, you would end up with the same result.
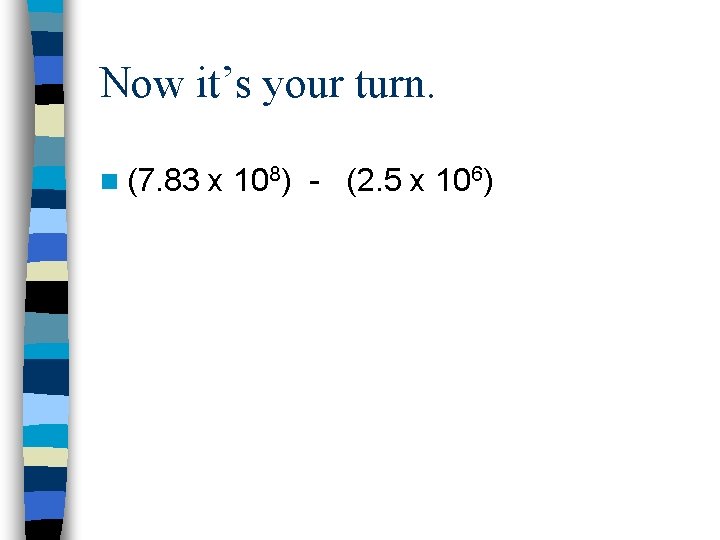
Now it’s your turn. n (7. 83 x 108) - (2. 5 x 106)

Extended Examples n (7. 45 x 108) - 11, 610, 000
- Slides: 15