Adders and Subtractors Discussion D 4 1 Adders

Adders and Subtractors Discussion D 4. 1

Adders and Subtractors • • Adders Carry and Overflow Subtractors Adder-Subtractor
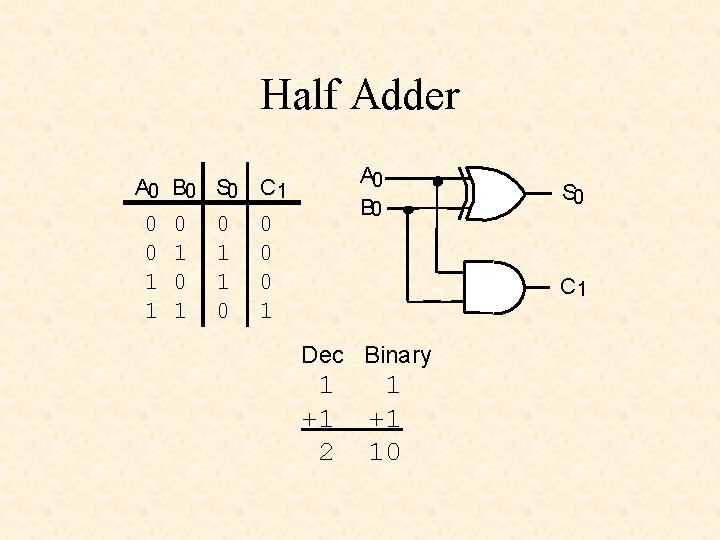
Half Adder A 0 B 0 S 0 0 0 1 1 0 1 0 1 1 0 A 0 B 0 C 1 0 0 0 1 S 0 C 1 Dec Binary 1 +1 2 1 +1 10

Multiple-bit Addition A 3 A 2 A 1 A 0 B 3 B 2 B 1 B 0 A 0 1 A B B 0 1 1 0 0 1 1 1 0 0 Ci+1 +Ci Ai +Bi Si
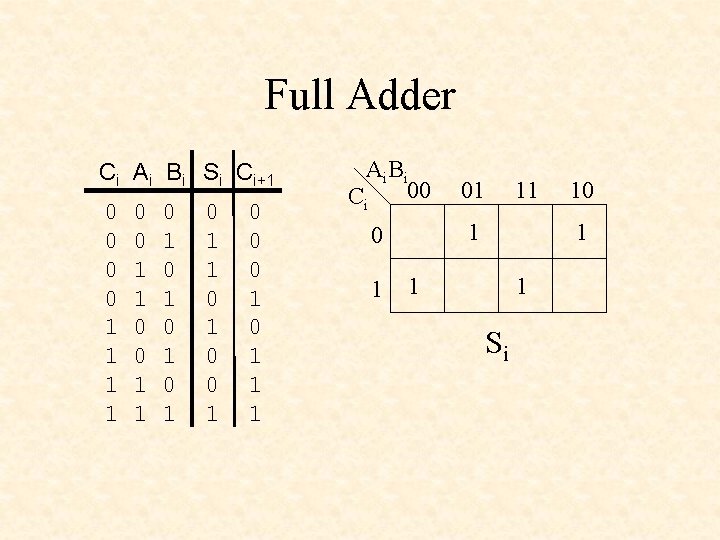
Full Adder Ci Ai Bi Si Ci+1 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 Ai B i 00 C i 11 1 01 10 1 1 1 Si
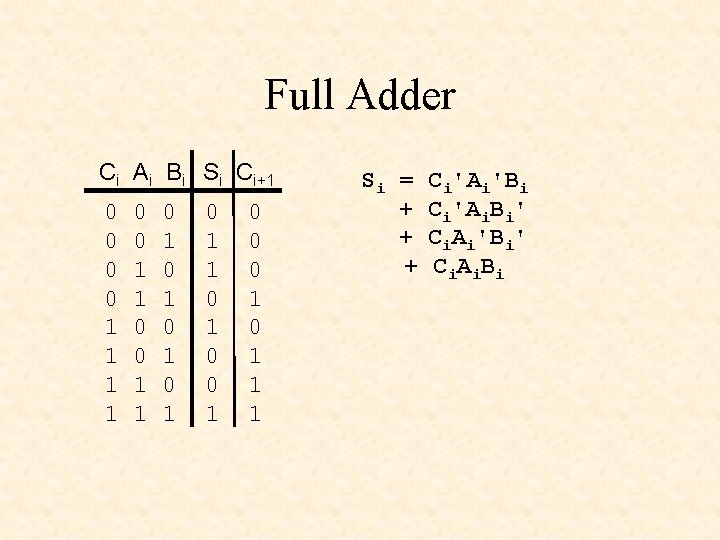
Full Adder Ci Ai Bi Si Ci+1 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 Si = + + + Ci'Ai'Bi Ci'Ai. Bi' Ci. Ai'Bi' C i. A i. B i

Full Adder Si = + + + Ci'Ai'Bi Ci'Ai. Bi' Ci. Ai'Bi' C i. A i. B i Si = Ci'(Ai'Bi + Ai. Bi') + Ci(Ai'Bi' + Ai. Bi) Si = Ci'(Ai + Ci(Ai Si = Ci B i) Bi)' (Ai B i)
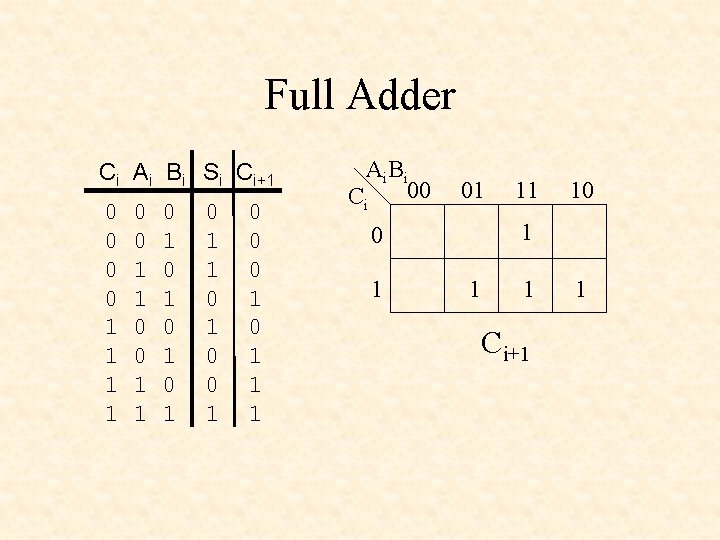
Full Adder Ci Ai Bi Si Ci+1 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 Ai B i 00 C i 01 10 1 11 1 1 Ci+1 1
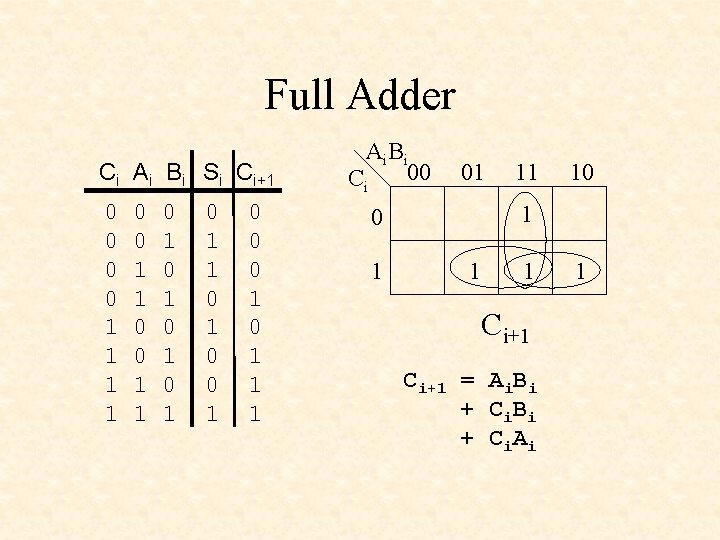
Full Adder Ci Ai Bi Si Ci+1 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 Ai B i 00 Ci 01 10 1 11 1 1 Ci+1 = Ai. Bi + C i. B i + C i. A i 1
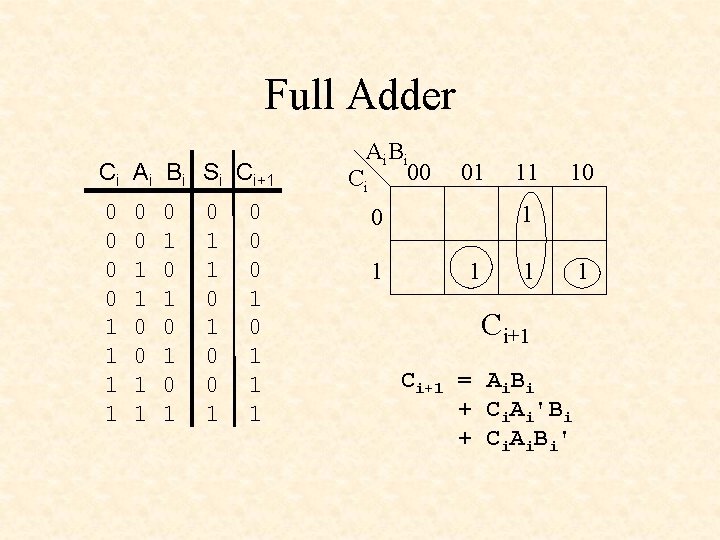
Full Adder Ci Ai Bi Si Ci+1 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 Ai B i 00 Ci 01 10 1 11 1 1 Ci+1 = Ai. Bi + Ci. Ai'Bi + C i. A i. B i' 1

Full Adder Ci+1 = Ai. Bi + Ci. Ai'Bi + C i. A i. B i' Ci+1 = Ai. Bi + Ci(Ai'Bi + Ai. Bi') Ci+1 = Ai. Bi + Ci(Ai Recall: Si = Ci B i) (Ai Ci+1 = Ai. Bi + Ci(Ai B i)
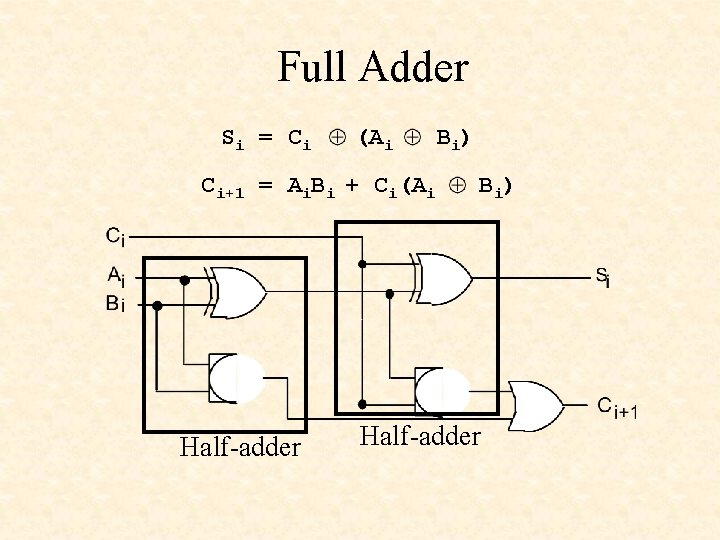
Full Adder Si = Ci (Ai Ci+1 = Ai. Bi + Ci(Ai Half-adder B i) Half-adder
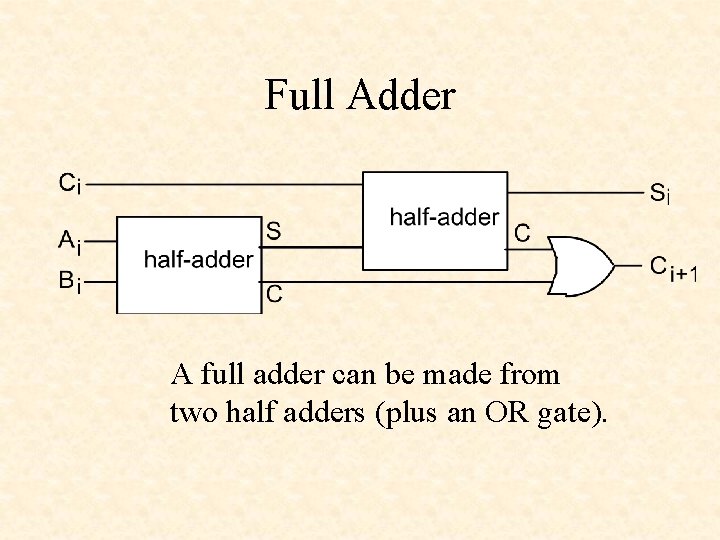
Full Adder A full adder can be made from two half adders (plus an OR gate).
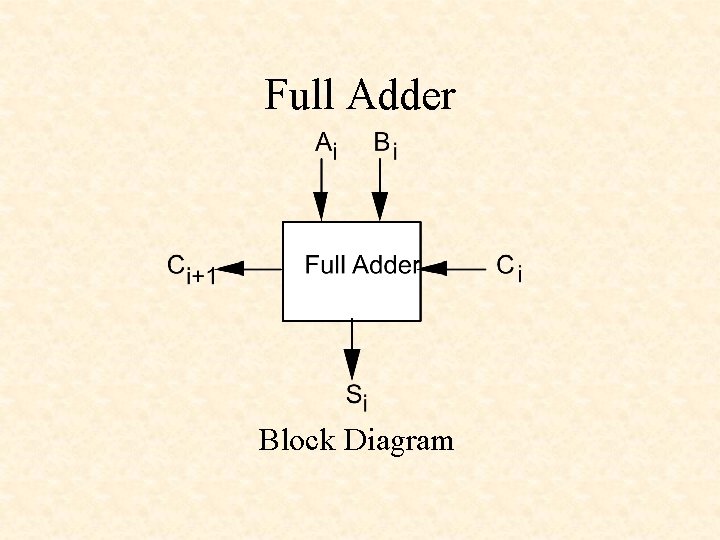
Full Adder Block Diagram
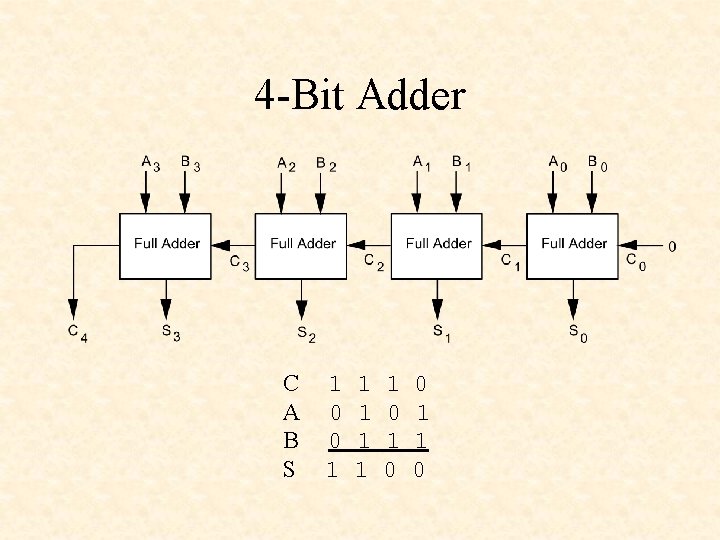
4 -Bit Adder C A B S 1 0 0 1 1 1 0 1 0 0 1 1 0
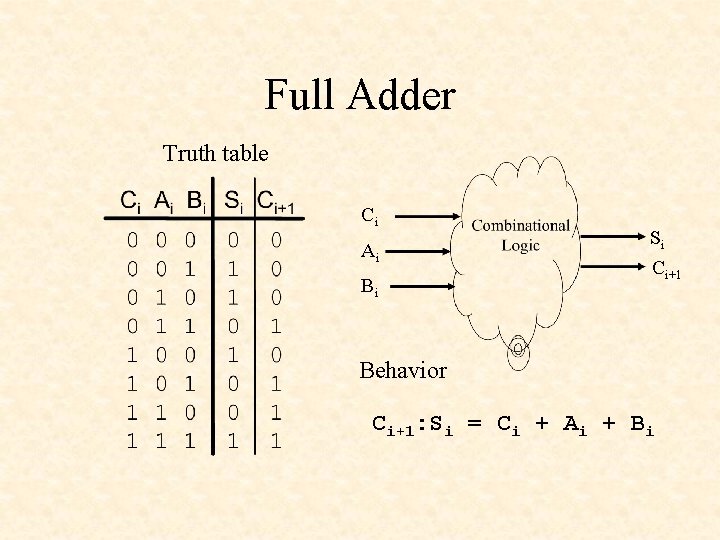
Full Adder Truth table Ci Ai Bi Si Ci+1 Behavior Ci+1: Si = Ci + Ai + Bi
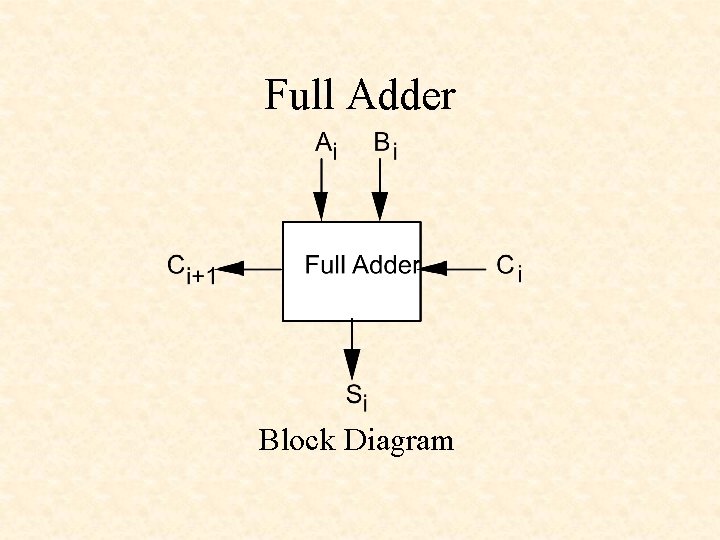
Full Adder Block Diagram
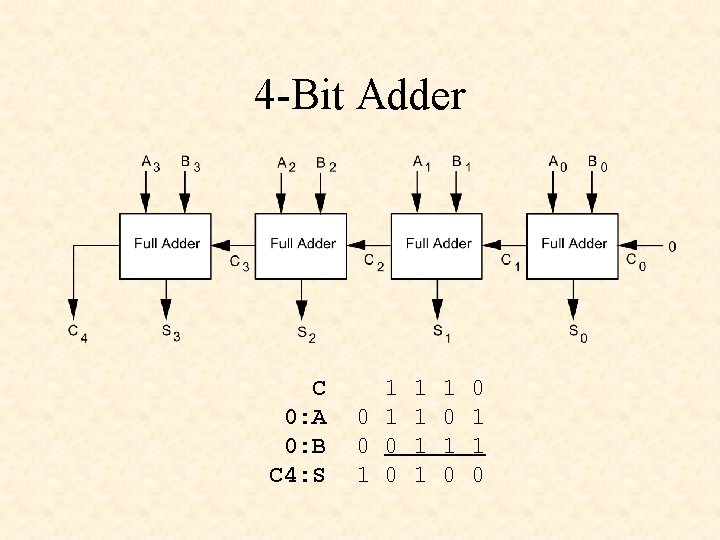
4 -Bit Adder C 0: A 0: B C 4: S 1 0 0 1 1 1 0 1 0 0 1 1 0

library IEEE; use IEEE. STD_LOGIC_1164. all; use IEEE. STD_LOGIC_unsigned. all; entity adder 4 is port( A : in STD_LOGIC_VECTOR(3 downto 0); B : in STD_LOGIC_VECTOR(3 downto 0); carry : out STD_LOGIC; S : out STD_LOGIC_VECTOR(3 downto 0) ); end adder 4; architecture adder 4 of adder 4 is begin process(A, B) variable temp: STD_LOGIC_VECTOR(4 downto 0); begin temp : = ('0' & A) + ('0' & B); S <= temp(3 downto 0); carry <= temp(4); end process; end adder 4;
4 -Bit Adder

Adders and Subtractors • • Adders Carry and Overflow Subtractors Adder-Subtractor

Carry and Overflow Binary Dec 53 +25 78 0 0 35 0 +19 4 E C = 0 0 V=0 Hex 1 0 0 1 1 1 0 0 0 1 1 0 1 0 1 1 0 Note no carry from bit 6 to bit 7 and no carry from bit 7 to C.

Carry and Overflow Binary Dec 53 +91 144 1 0 35 0 +5 B 90 C = 0 1 V=1 Hex 1 0 1 1 0 0 1 1 1 0 0 Note carry from bit 6 to bit 7 but no carry from bit 7 to C. Thinking SIGNED we added two positive numbers and got a negative result. This can’t be correct! Therefore, the OVERFLOW bit, V, is set to 1. Correct answer (144) is outside the range -128 to +127.

Carry and Overflow Binary Dec 1 0 35 1 +D 3 108 C = 1 0 V=0 Hex 53 - 45 8 Ignore carry 1 0 1 1 0 0 1 1 1 0 0 Note carry from bit 6 to bit 7 and carry from bit 7 to C. Thinking SIGNED we added a positive number to a negative number and got the correct positive answer. Therefore, the OVERFLOW bit, V, is cleared to 0. Correct answer (8) is inside the range -128 to +127.

Carry and Overflow Binary 0 0 1 1 0 1 0 0 1 1 0 9 E - 98 1 1 0 0 1 1 - 45 +D 3 - 143 171 C = 1 0 1 1 1 0 0 0 1 Ignore Note no carry from bit 6 to bit 7 V = 1 carry Dec Hex but there is a carry from bit 7 to C. Thinking SIGNED we added two negative numbers and got a positive answer. This must be wrong! Therefore, the OVERFLOW bit, V, is set to 1. Correct answer (-143) is outside the range -128 to +127.

Overflow • Note that the overflow bit was set whenever we had a carry from bit 6 to bit 7, but no carry from bit 7 to C. • It was also set when we had a carry from bit 7 to C, but no carry from bit 6 to bit 7. • Upshot: The overflow bit is the EXCLUSIVE-OR of a carry from bit 6 to bit 7 and a carry from bit 7 to C.

Adders and Subtractors • • Adders Carry and Overflow Subtractors Adder-Subtractor
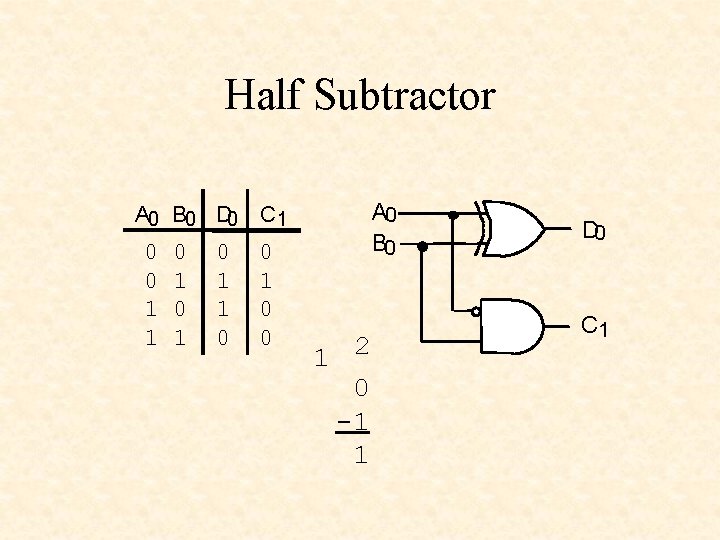
Half Subtractor A 0 B 0 D 0 0 0 1 1 0 1 0 1 1 0 A 0 B 0 C 1 0 0 1 2 0 -1 1 D 0 C 1

Multiple-bit Subtraction A 3 A 2 A 1 A 0 1 0 1 1 A 0 B 0 1 1 B 3 B 2 B 1 B 0 1 1 1 0 Ci+1 - Ci Ai - Bi Di
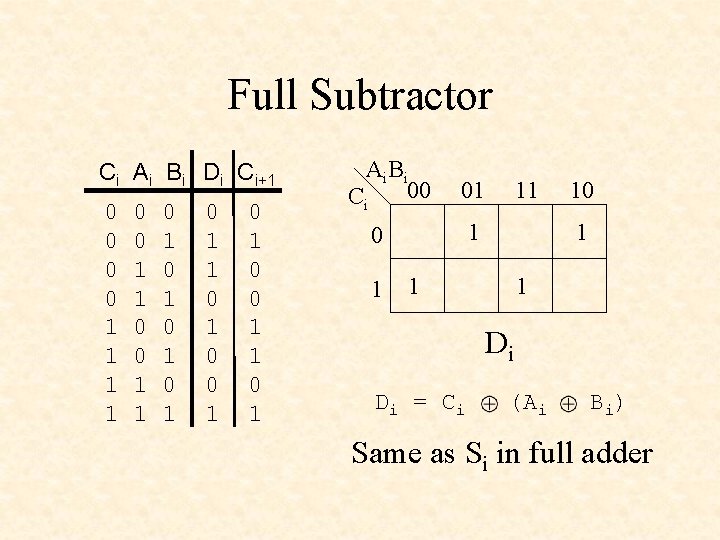
Full Subtractor Ci Ai Bi Di Ci+1 0 0 1 1 0 1 0 1 0 1 0 0 1 1 0 1 Ai B i 00 Ci 01 1 0 1 11 10 1 1 1 Di Di = Ci (Ai B i) Same as Si in full adder
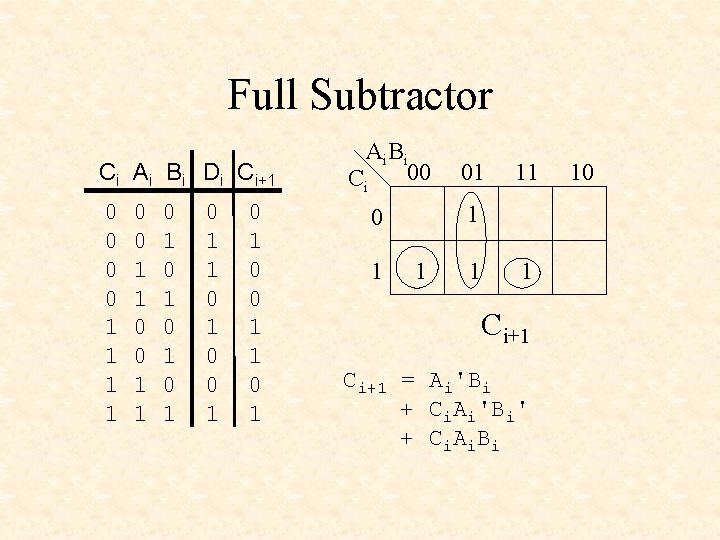
Full Subtractor Ci Ai Bi Di Ci+1 0 0 1 1 0 1 0 1 0 1 0 0 1 1 0 1 Ai B i 00 Ci 11 1 01 1 Ci+1 = Ai'Bi + Ci. Ai'Bi' + C i. A i. B i 10

Full Subtractor Ci+1 = Ai'Bi + Ci. Ai'Bi' + C i. A i. B i Ci+1 = Ai'Bi + Ci(Ai'Bi' + Ai. Bi) Ci+1 = Ai'Bi + Ci(Ai Recall: Di = Ci (Ai Bi)' B i) Ci+1 = Ai'Bi + Ci(Ai Bi)'
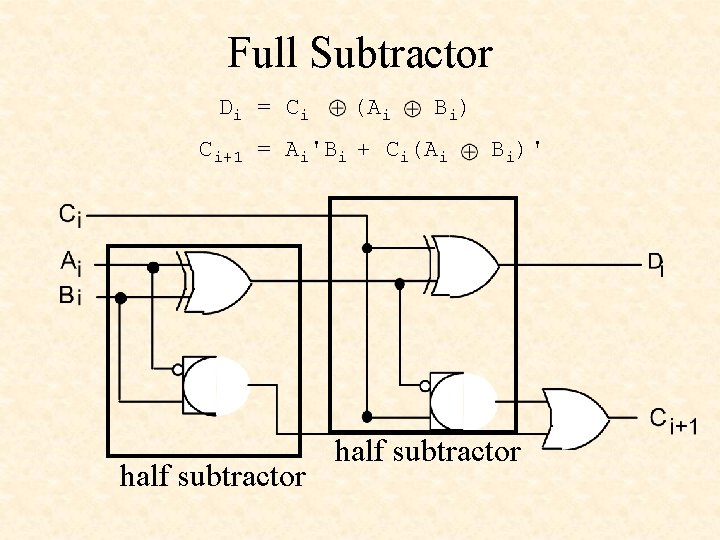
Full Subtractor Di = Ci (Ai B i) Ci+1 = Ai'Bi + Ci(Ai half subtractor Bi)' half subtractor

Adders and Subtractors • • Adders Carry and Overflow Subtractors Adder-Subtractor
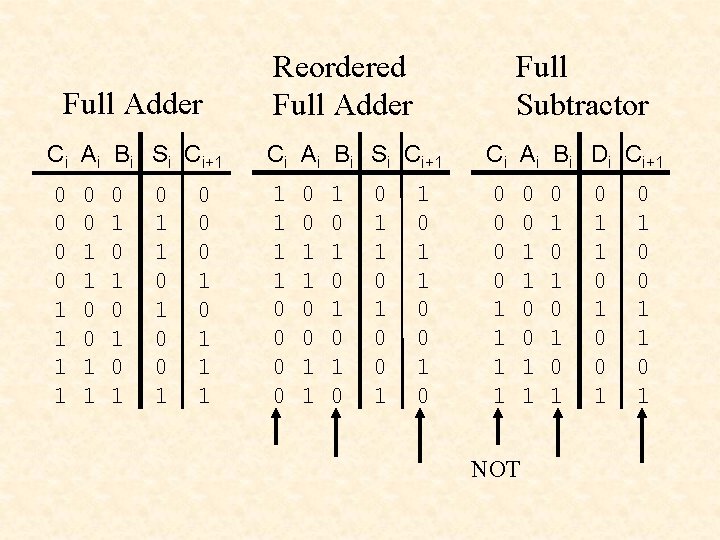
Full Adder Reordered Full Adder Full Subtractor Ci Ai Bi Si Ci+1 Ci Ai Bi Di Ci+1 0 0 1 1 1 1 0 0 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 0 1 0 0 1 1 0 0 1 0 NOT 0 0 1 1 0 1 0 1 0 1 0 0 1 1 0 1
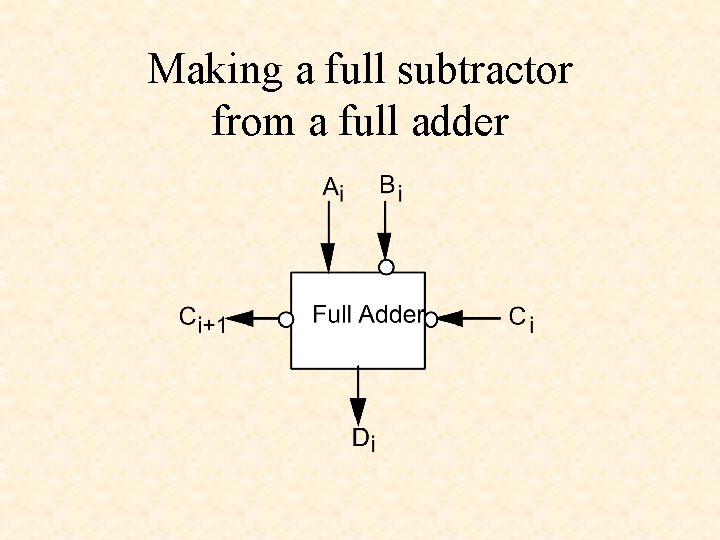
Making a full subtractor from a full adder
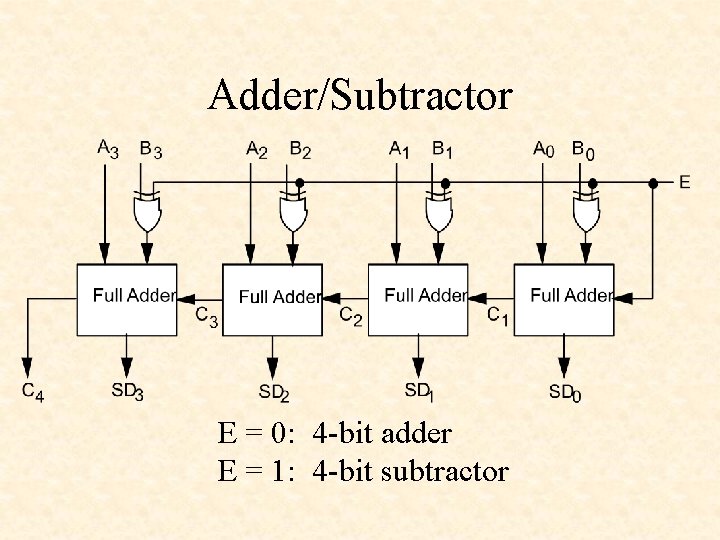
Adder/Subtractor E = 0: 4 -bit adder E = 1: 4 -bit subtractor
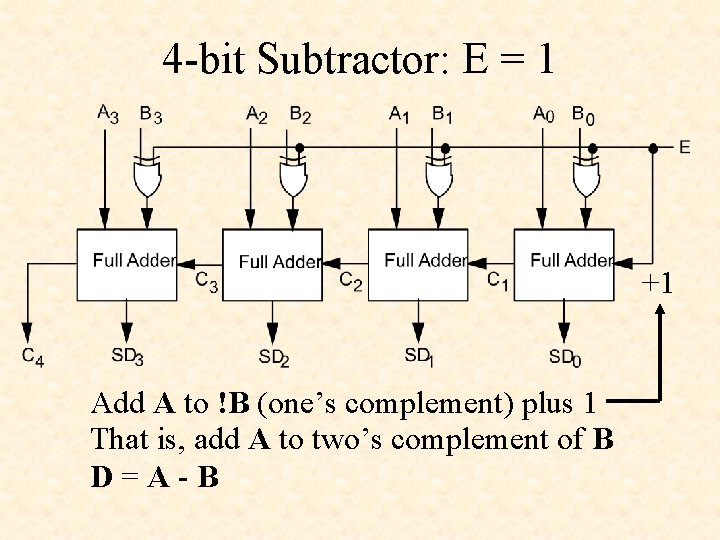
4 -bit Subtractor: E = 1 +1 Add A to !B (one’s complement) plus 1 That is, add A to two’s complement of B D=A-B
- Slides: 38