Add the vectors A B and C shown

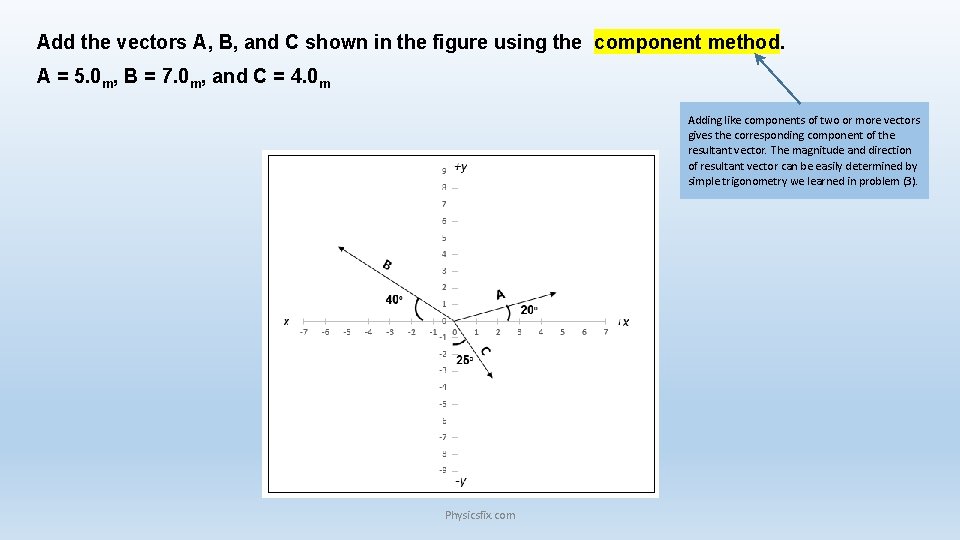
Add the vectors A, B, and C shown in the figure using the component method. A = 5. 0 m, B = 7. 0 m, and C = 4. 0 m Adding like components of two or more vectors gives the corresponding component of the resultant vector. The magnitude and direction of resultant vector can be easily determined by simple trigonometry we learned in problem (3). Physicsfix. com

Add the vectors A, B, and C shown in the figure using the component method. A = 5. 0 m, B = 7. 0 m, and C = 4. 0 m Solution: Here we learn another way to add two or more vectors. This method is called component method. To add vectors in this problem we need to; 1. Calculate the components of each vector 2. Add like components to calculate corresponded component of resultant vector R x = Ax + Bx + Cx 3. R y = A y + B y + Cy Then determine the magnitude and direction of R R 2 = Rx 2 + Ry 2 and tg θ = Ry / Rx Physicsfix. com

Add the vectors A, B, and C shown in the figure using the component method. A = 5. 0 m, B = 7. 0 m, and C = 4. 0 m Now we start step by step Step 1: Calculate components for each vector Ax = A Cos 20⁰ = + (5. 0 m) Cos 20⁰ Ax = + 4. 7 m If a component of a vector points along negative part of axis, its sign will be negative. Bx = - B Cos 40⁰ = - (7. 0 m) Cos 40⁰ Bx = -5. 4 m Cx = +C sin 25⁰ = + (4. 0) Sin 25⁰ Cx = + 1. 7 m Projection of “C” along “X’ axis is C x = C Cos θ whereas θ is the angle it makes with “X” axis. So we can write: Cx = C Cos (90 -25) = C Cos (65⁰) and we know Cos (90 -α) = Sin (α) Cos 65⁰ = Sin 25⁰ Ay = +A Sin 20⁰ = + (5. 0 m) Sin 20⁰ Ay = +1. 7 m By = +B Sin 40⁰ = + (7. 0 m) Sin 40⁰ By = + 4. 5 m Cy = - C Cos 25⁰ = - (4. 0) Cos 25⁰ Cy= - 3. 6 m Physicsfix. com

Add the vectors A, B, and C shown in the figure using the component method. A = 5. 0 m, B = 7. 0 m, and C = 4. 0 m Step 2: Adding Like Components Rx = Ax + Bx + Cx = +4. 7 m + (-5. 4 m) + 1. 7 m Rx = + 1. 0 m Ry = Ay + By + Cy = +1. 7 m +4. 5 m + (-3. 6 m) Ry = + 2. 6 m Positive sign shows that the components of the resultant vector point along +x and +y axes. Step 3: Calculating the Magnitude and Direction of Vector R 2 = Rx 2 + Ry 2 = (1)2 + (2. 6)2 → R= 2. 8 m Magnitude of the resultant vector tg θ = Resultant vector makes an angle of 69⁰ with +x axis. Physicsfix. com

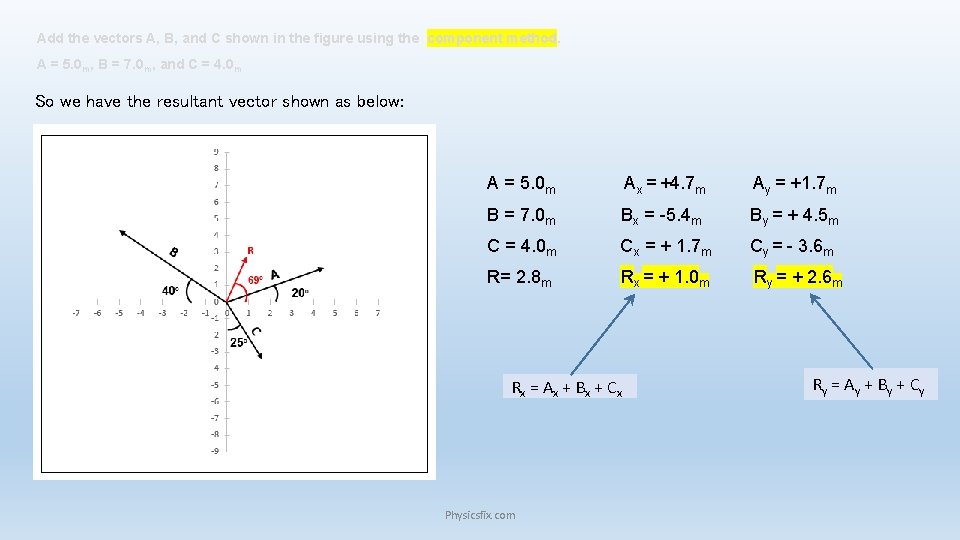
Add the vectors A, B, and C shown in the figure using the component method. A = 5. 0 m, B = 7. 0 m, and C = 4. 0 m So we have the resultant vector shown as below: A = 5. 0 m Ax = +4. 7 m Ay = +1. 7 m B = 7. 0 m Bx = -5. 4 m By = + 4. 5 m C = 4. 0 m Cx = + 1. 7 m Cy = - 3. 6 m R= 2. 8 m Rx = + 1. 0 m Ry = + 2. 6 m R x = A x + B x + Cx Physicsfix. com R y = A y + B y + Cy