Add and subtract between 1 and 7 digit

• • • Add and subtract between 1 and 7 digit numbers with and without calculator. Multi-step calculations. Use approximation to estimate answers. Define and give everyday examples of negative numbers. Order and compare negative numbers, including in everyday situations. E 1 Add and subtract single digit numbers to 10, add and subtract number of given objects, state number bonds and subtraction facts, use a calculator to check whole number addition and subtraction calculations. Work out problems including +, – and =. E 2 State pairs of numbers that add up to 10 and subtraction facts that total to 10, list words that mean addition and subtraction, add two digit whole numbers, add single and two digit whole numbers. Subtract one and two digit numbers from whole numbers with two digits. E 3 State addition and subtraction facts totalling to 20, add three-digit whole numbers with and without calculator. Subtract single, double and triple digit numbers from three digit whole numbers. Use calculator to add, subtract, check and solve problems, approximate answers to calculations. L 1 Add and subtract up to 7 digit numbers with and without calculator. Check answers using calculator. Define and use negative numbers in everyday situations. L 2 Calculate with two or more operations in a sequence with and without calculator. Record negative numbers in digit form, arrange positive and negative numbers in order of value, compare positive and negative numbers.

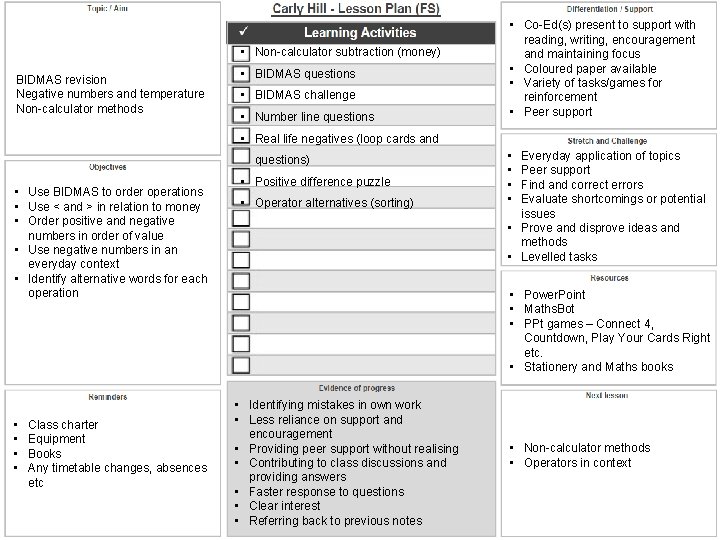
• Non-calculator subtraction (money) BIDMAS revision Negative numbers and temperature Non-calculator methods • BIDMAS questions • BIDMAS challenge • Number line questions • Co-Ed(s) present to support with reading, writing, encouragement and maintaining focus • Coloured paper available • Variety of tasks/games for reinforcement • Peer support • Real life negatives (loop cards and questions) • Use BIDMAS to order operations • Use < and > in relation to money • Order positive and negative numbers in order of value • Use negative numbers in an everyday context • Identify alternative words for each operation • • Class charter Equipment Books Any timetable changes, absences etc • Positive difference puzzle • Operator alternatives (sorting) • • Everyday application of topics Peer support Find and correct errors Evaluate shortcomings or potential issues • Prove and disprove ideas and methods • Levelled tasks • Power. Point • Maths. Bot • PPt games – Connect 4, Countdown, Play Your Cards Right etc. • Stationery and Maths books • Identifying mistakes in own work • Less reliance on support and encouragement • Providing peer support without realising • Contributing to class discussions and providing answers • Faster response to questions • Clear interest • Referring back to previous notes • Non-calculator methods • Operators in context

This week: • BIDMAS recap • Negative numbers • Non-calculator methods Carly Hill Maths

Why do I need to know this? • Calculate accurately with multiple operators • Tell the difference between positive and negative numbers When will I need to use this? • Working with temperature • Understanding debit and credit in bank accounts • Following instructions • Working with formula, e. g area and perimeter

You changed electricity provider and they predict your next bill will be one hundred and ninety pounds less than last year. If you paid £ 786 last year, how much will you pay this year? 786 – 190 = £ 596 1 7 8 6 – 1 9 0 596 £ 6

College success rates: • Exam success > 95% • A grade passes > 15% • Students withdrawing from a course < 5% From the information above: • Were the A grade passes greater than or less than 15%? • Students withdrawing from a course were less than 5%, true or false? • An advertisement for a college trip states that the cost will be > £ 18. Jamal has £ 17, has he got enough money?

BIDMAS 8 - 3 x 2 = 6 8 – 6 = 2 20 ÷ 10 = 2 20 + 20 ÷ 10 = 20 + 2 = 22 5 x 3 + 12 = 6 x 2 – 9 = 5 x 3 = 15 15 + 12 = 27 6 x 2 = 12 12 – 9 = 3 2 + 5 = 7 2 + 5 – 1 = 7 – 1 = 6 3 x 2 = 6 10 - 3 x 2 + 4 = 6 + 4 = 10 10 – 10 = 0 20 ÷ 10 = 2 20 + 20 ÷ 10 x 3 = 2 x 3 = 6 20 + 6 = 26 5 x 3 = 15 5 x 3 + 12 – 4 = 15 + 12 = 27 27 – 4 = 23 4 x 6 = 24 4 x 6 x 2 – 9 = 24 x 2 = 48 48 – 9 = 39 5 - 2 = 3 32 = 9 16 + (5 – 2)2 x 2 = 9 x 2 = 18 16 + 18 = 34

The ultimate BIDMAS challenge… 35 14 37 5 + 7 x 3 – 6 ÷ 2 + 4 27 6 ÷ 2 = 3 7 x 3 = 21 21 + 5 + 4 = 30 30 – 3 = 27 19

Number of the day: 15 • 15 + 12 • 15 + 29 • 15 - 16 • 15 x 5 • 15 ÷ 3 • Write five prime numbers

Types of number Negative Positive • Which side of the number line are positive numbers? • Where are the negative numbers?

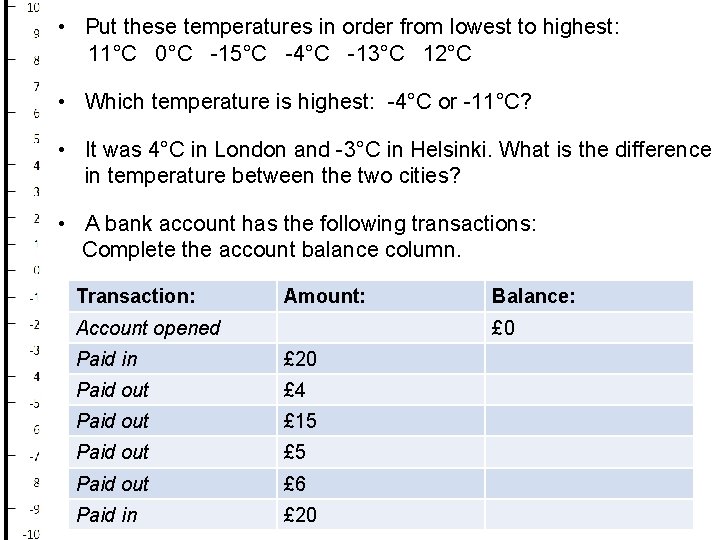
• Put these temperatures in order from lowest to highest: 11°C 0°C -15°C -4°C -13°C 12°C • Which temperature is highest: -4°C or -11°C? • It was 4°C in London and -3°C in Helsinki. What is the difference in temperature between the two cities? • A bank account has the following transactions: Complete the account balance column. Transaction: Amount: Account opened Balance: £ 0 Paid in £ 20 Paid out £ 4 Paid out £ 15 Paid out £ 6 Paid in £ 20

Operators

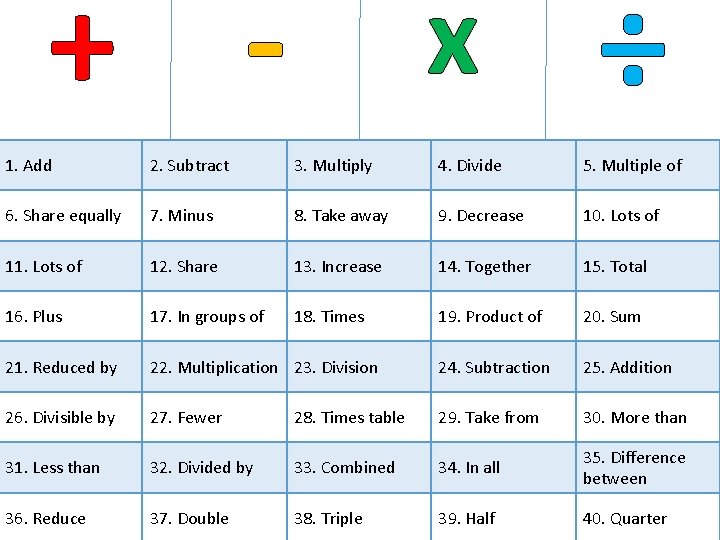
+ - x ÷ 1. Add 2. Subtract 3. Multiply 4. Divide 5. Multiple of 6. Share equally 7. Minus 8. Take away 9. Decrease 10. Lots of 11. Lots of 12. Share 13. Increase 14. Together 15. Total 16. Plus 17. In groups of 18. Times 19. Product of 20. Sum 21. Reduced by 22. Multiplication 23. Division 24. Subtraction 25. Addition 26. Divisible by 27. Fewer 28. Times table 29. Take from 30. More than 31. Less than 32. Divided by 33. Combined 34. In all 35. Difference between 36. Reduce 37. Double 38. Triple 39. Half 40. Quarter

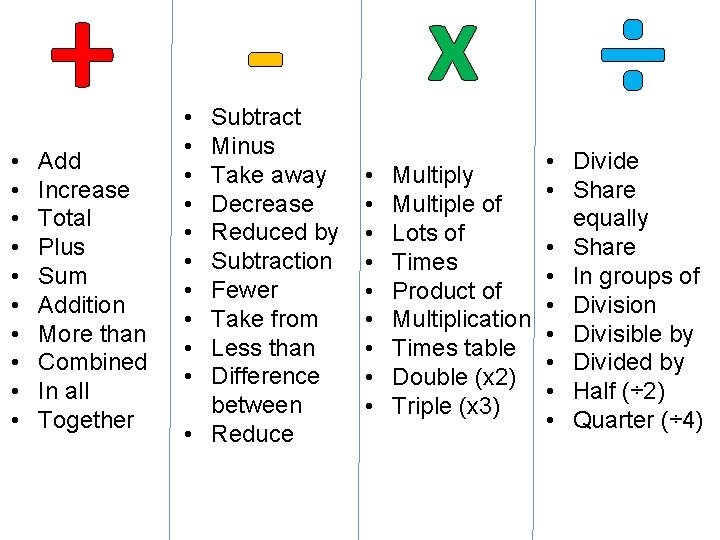
+ • • • Add Increase Total Plus Sum Addition More than Combined In all Together • • • Subtract Minus Take away Decrease Reduced by Subtraction Fewer Take from Less than Difference between • Reduce x • • • Multiply Multiple of Lots of Times Product of Multiplication Times table Double (x 2) Triple (x 3) ÷ • Divide • Share equally • Share • In groups of • Division • Divisible by • Divided by • Half (÷ 2) • Quarter (÷ 4)

Positive Differences Choose 3 different numbers between 1 and 6… Work out the difference between the biggest and smallest pairs of numbers… What are the biggest and smallest possible values at the top of the pyramid? 6 1 5 6