Adaptive Meshes on the Sphere CubedSpheres versus LatitudeLongitude

Adaptive Meshes on the Sphere: Cubed-Spheres versus Latitude-Longitude Grids Christiane Jablonowski University of Michigan Dec/8/2006

Acknowledgments The AMR comparison is based on a joint paper with Amik St-Cyr and collaborators from NCAR, submitted to Monthly Weather Review in November 2006 The AMR Spectral Element Model was mainly developed by Amik St-Cyr, John Dennis & Steve Thomas (NCAR) The AMR FV model is documented in Jablonowski (2004), Jablonowski et al. (2004, 2006) Contributors to the AMR FV model are Michael Herzog (GFDL) & Joyce Penner (UM) Robert Oehmke (NCAR) & Quentin Stout (UM) Bram van Leer (UM) & Ken Powell (UM)

Overview Computational Grids on the Sphere Adaptive mesh refinement (AMR) techniques Why are we interested in variable resolutions / multi-scales? Overview of two AMR shallow water models Finite volume (FV) model Spectral element model (SEM) Results: Static and dynamic adaptations 2 D shallow water experiments Conclusions and Outlook
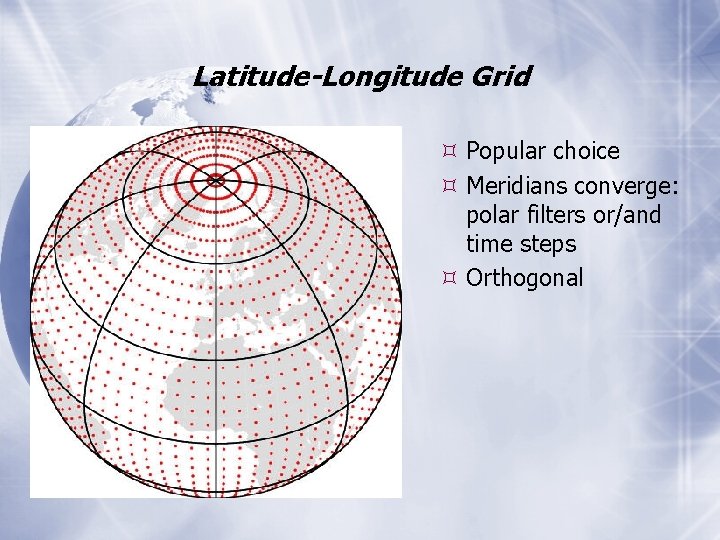
Latitude-Longitude Grid Popular choice Meridians converge: polar filters or/and time steps Orthogonal

Platonic solids - Regular grid structures Platonic solids can be enclosed in a sphere

Cubed Sphere Geometry Advection of a cosine bell around the sphere (12 days) at a 45 o angle Courtesy of Ram Nair (NCAR)
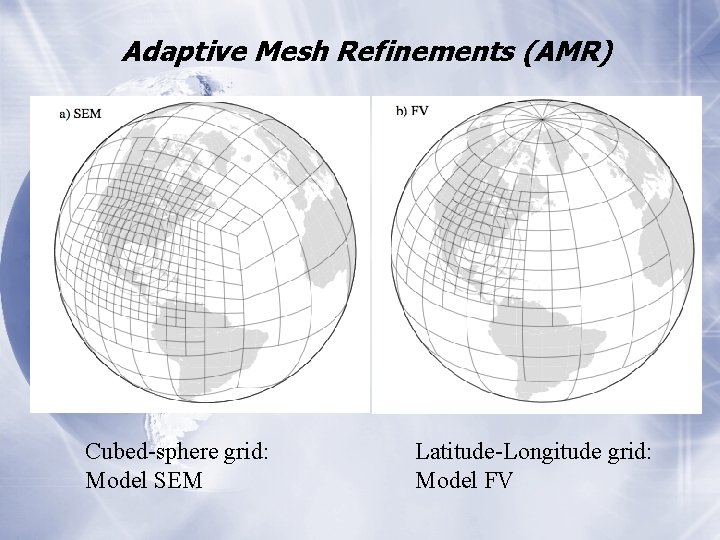
Adaptive Mesh Refinements (AMR) Cubed-sphere grid: Model SEM Latitude-Longitude grid: Model FV

SEM: Grid Points within Spectral Elements Circles: Gauss-Lobatto. Legendre (GLL) points for vectors Squares: Gauss-Lobatto (GL) points for scalars Elements are split in case of refinements
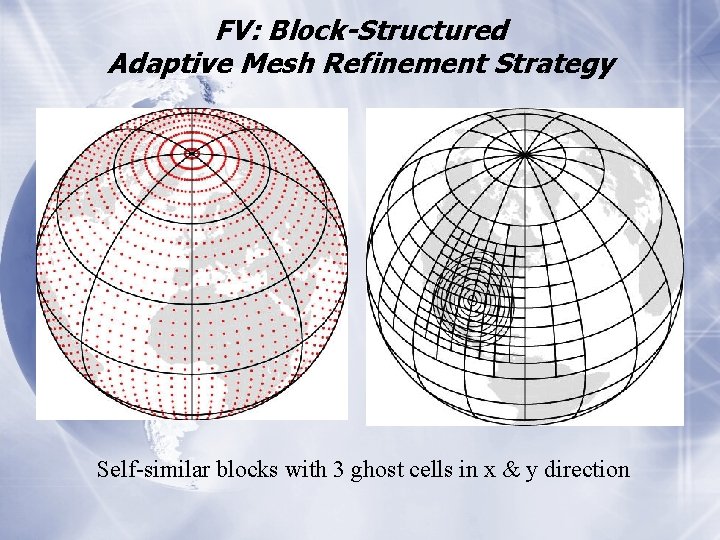
FV: Block-Structured Adaptive Mesh Refinement Strategy Self-similar blocks with 3 ghost cells in x & y direction

Other AMR Grids Model ICON Icosahedral grid with nested high-resolution regions under development at the German Weather Service (DWD) and MPI, Hamburg Source: DWD

Features of Interest in a Multi-Scale Regime Hurricane Frances September/5/2004 Hurricane Ivan
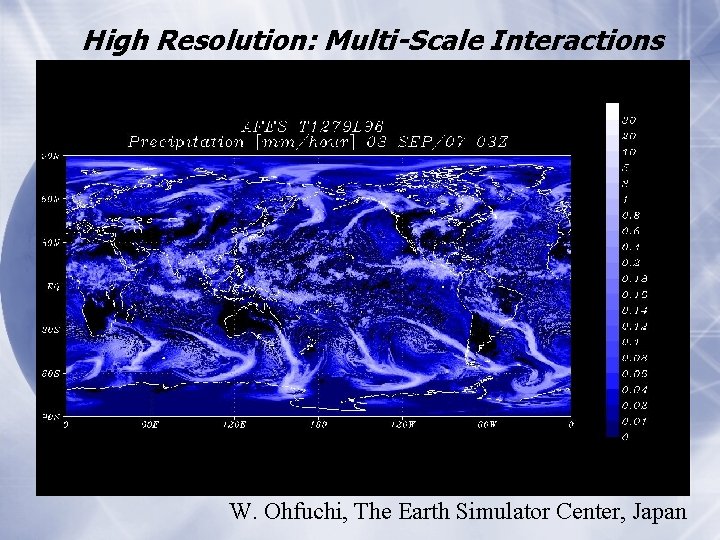
High Resolution: Multi-Scale Interactions 10 km resolution W. Ohfuchi, The Earth Simulator Center, Japan

AMR Transport of a Slotted Cylinder Model FV
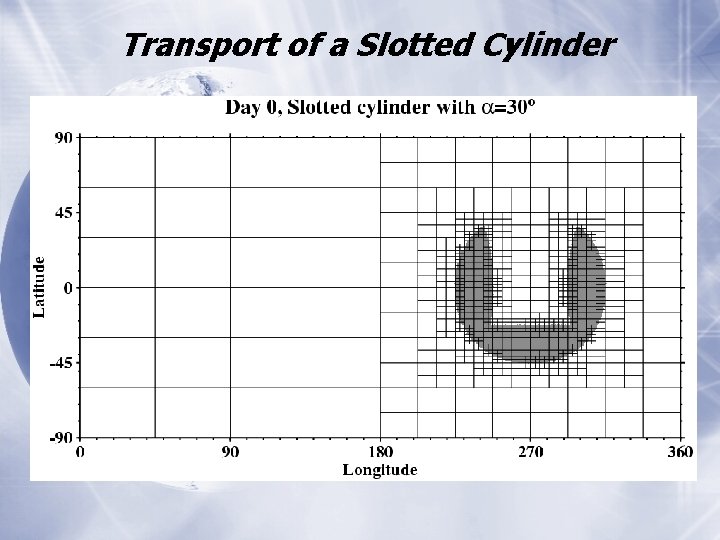
Transport of a Slotted Cylinder
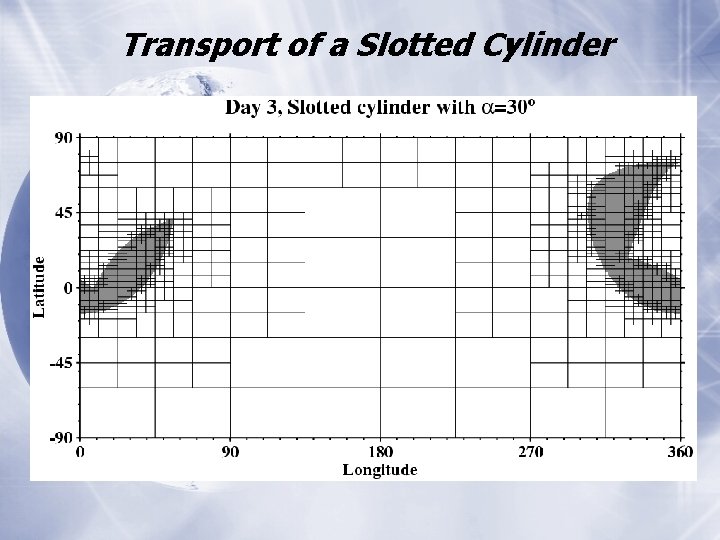
Transport of a Slotted Cylinder
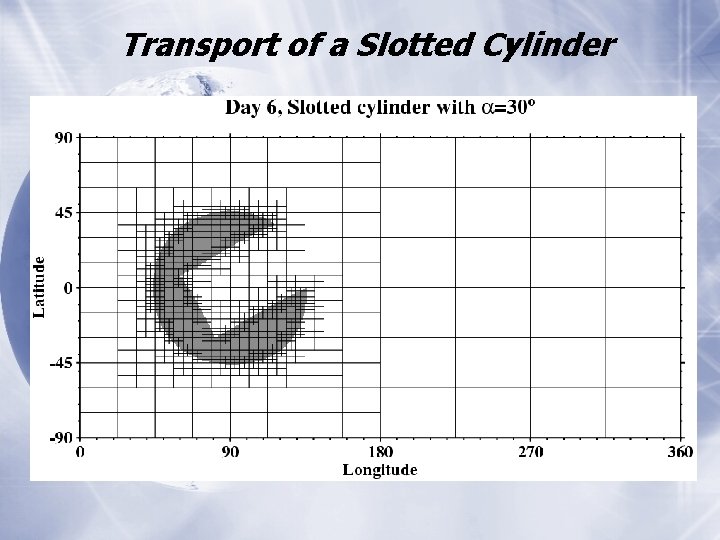
Transport of a Slotted Cylinder
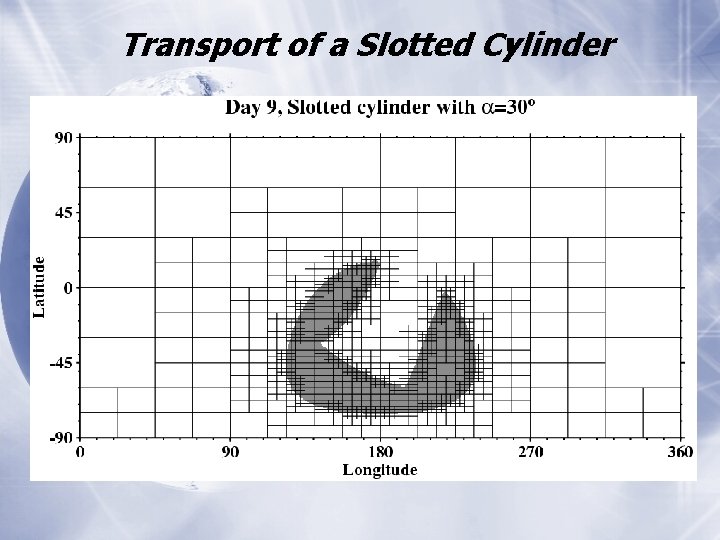
Transport of a Slotted Cylinder
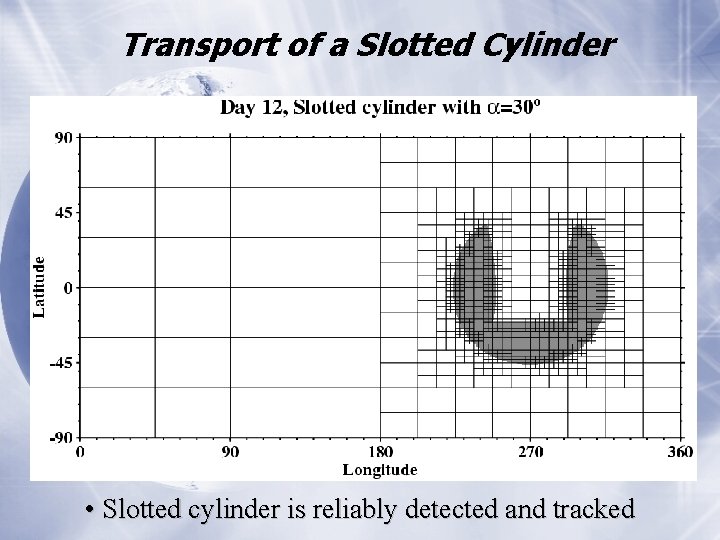
Transport of a Slotted Cylinder • Slotted cylinder is reliably detected and tracked

Shallow Water Equations Momentum equation in vector-invariant form Continuity equation vh horizontal velocity vector relative vorticity f Coriolis parameter K= 0. 5*(u 2 + v 2) kinetic energy D horizontal divergence, damping coefficient h free surface height, hs height of the orography g gravitational acceleration

Finite Volume (FV) Shallow Water Model l Developed by Lin and Rood (1996), Lin and Rood (1997) l 3 D version available (Lin 2004), built upon the SW model: l hydrostatic dynamical core used for climate and weather predictions l Currently part of NCAR’s, NASA’s and GFDL’s General Circulation Models l Numerics: Finite volume approach – – conservative and monotonic transport scheme upwind biased 1 D fluxes, operator splitting van Leer second order scheme for time-averaged numerical fluxes PPM third order scheme (piecewise parabolic method) for prognostic variables – Staggered grid (Arakawa D-grid) – Orthogonal Latitude-Longitude computational grid

Spectral Element (SEM) Shallow Water Model l Documented in Thomas and Loft (2002), St-Cyr and Thomas (2005), St-Cyr et al. (2006) l 3 D version available l Experimental tests within NCAR’s Climate Modeling Software Framework l Numerics: Spectral Elements – – – Non-conservative and non-monotonic Allows high-order numerical method Spectral convergence for smooth flows GLL and GL collocation points Non-orthogonal cubed-sphere computational grid

Overview of the AMR comparison 2 D shallow water tests: (Williamson et al. , JCP 1992) Dynamic refinements for pure advection experiments Cosine bell advection test (test case 1) Static refinements in regions of interest (test case 2) Dynamic refinements and refinement criteria: Flow over a mountain (test case 5) Rossby-Haurwitz wave with static refinements (test case 6)
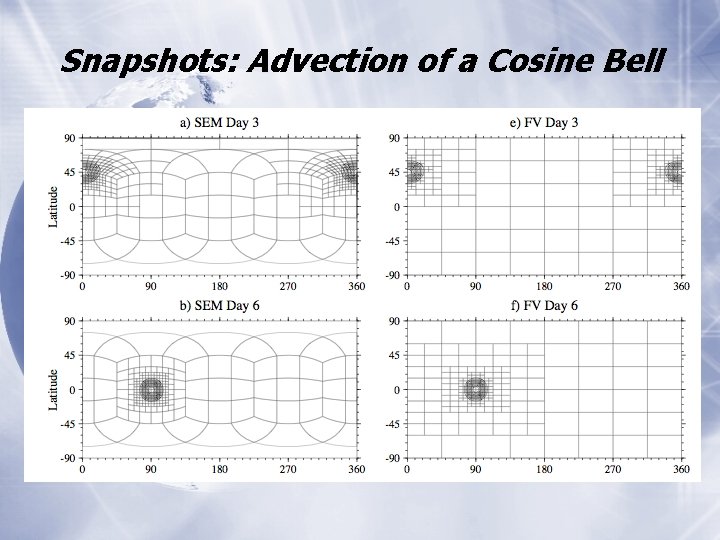
Snapshots: Advection of a Cosine Bell
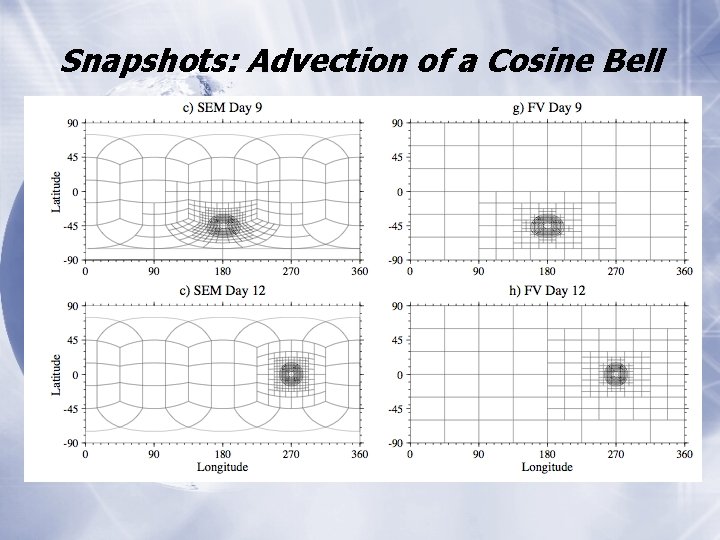
Snapshots: Advection of a Cosine Bell
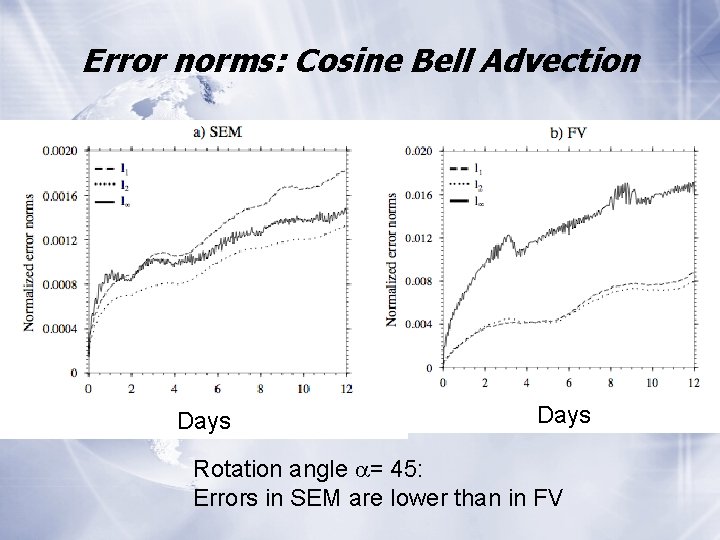
Error norms: Cosine Bell Advection Days Rotation angle = 45: Errors in SEM are lower than in FV
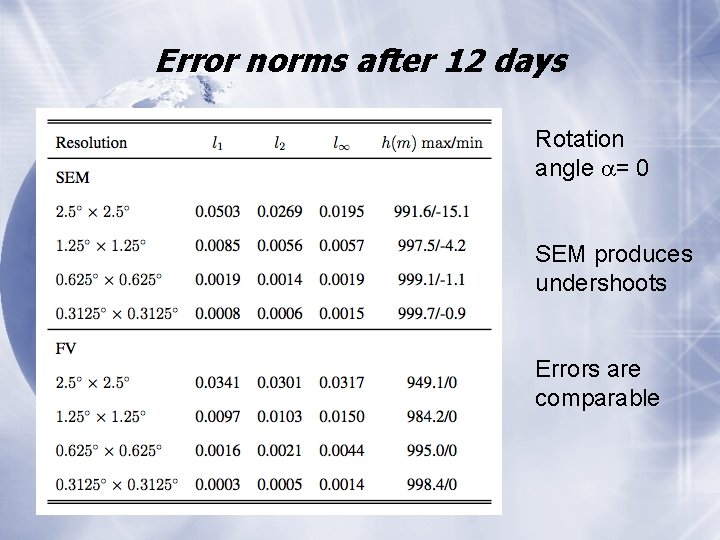
Error norms after 12 days Rotation angle = 0 SEM produces undershoots Errors are comparable
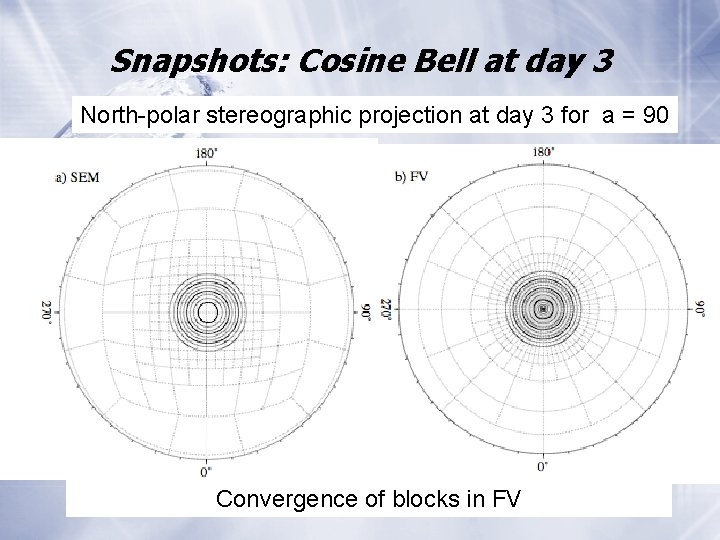
Snapshots: Cosine Bell at day 3 North-polar stereographic projection at day 3 for a = 90 Convergence of blocks in FV
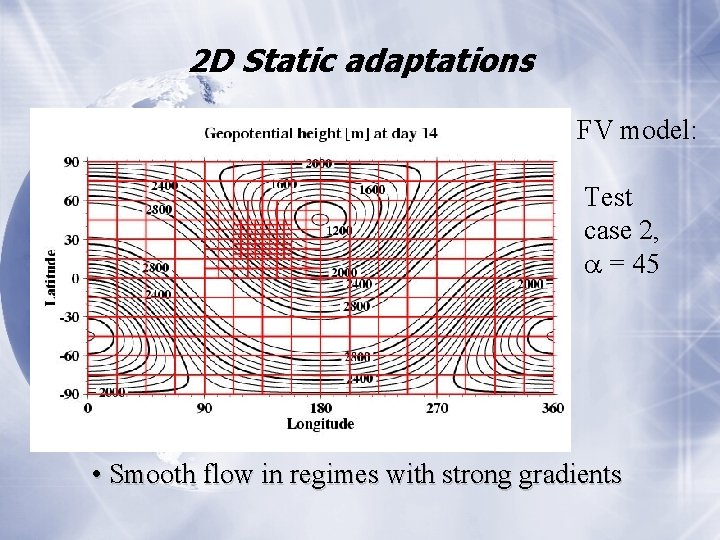
2 D Static adaptations FV model: Test case 2, = 45 • Smooth flow in regimes with strong gradients
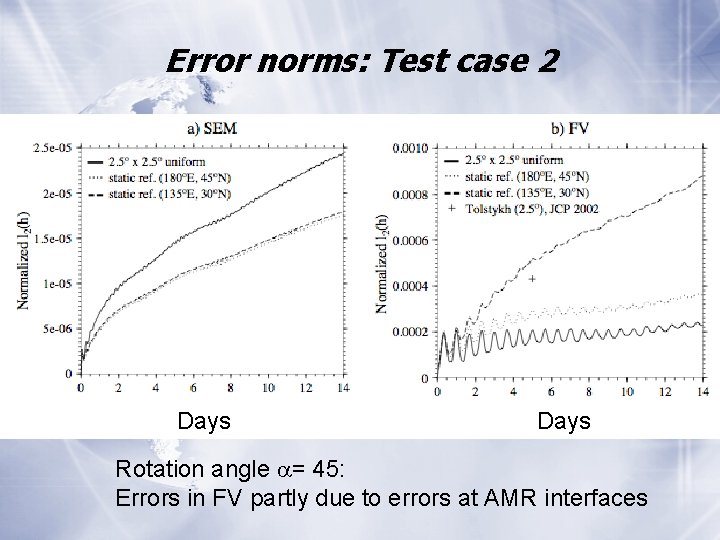
Error norms: Test case 2 Days Rotation angle = 45: Errors in FV partly due to errors at AMR interfaces

2 D Dynamic adaptations in FV Vorticity-based adaptation criterion 2 D shallow water test #5: 15 -day run
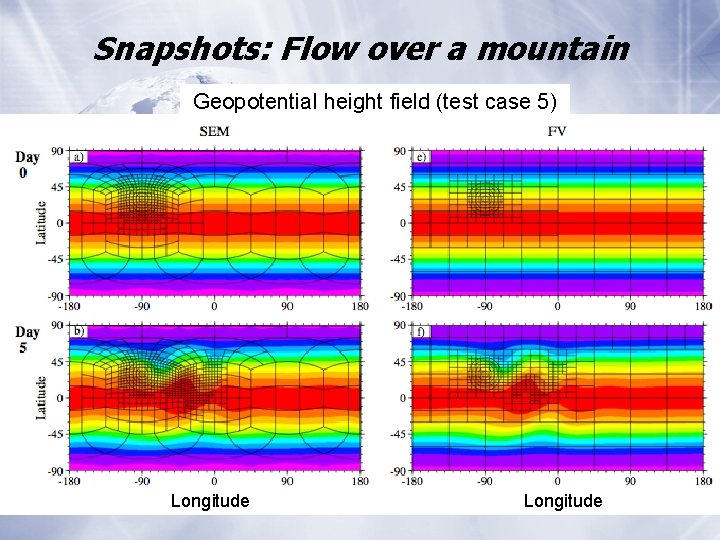
Snapshots: Flow over a mountain Geopotential height field (test case 5) Longitude
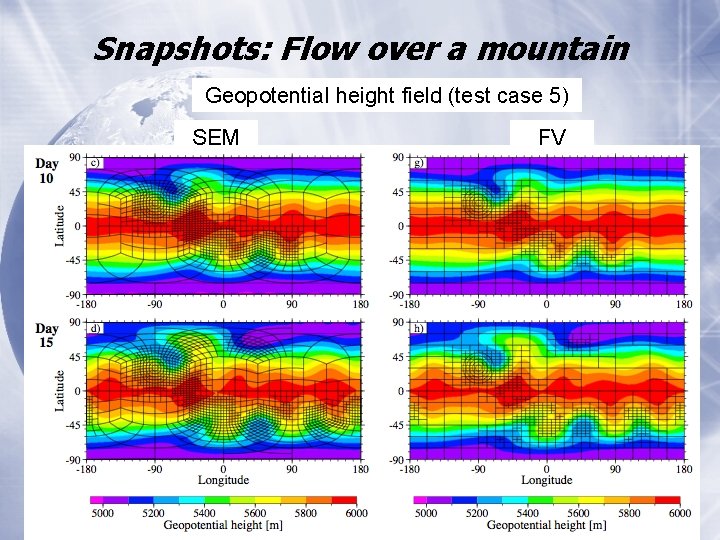
Snapshots: Flow over a mountain Geopotential height field (test case 5) SEM FV
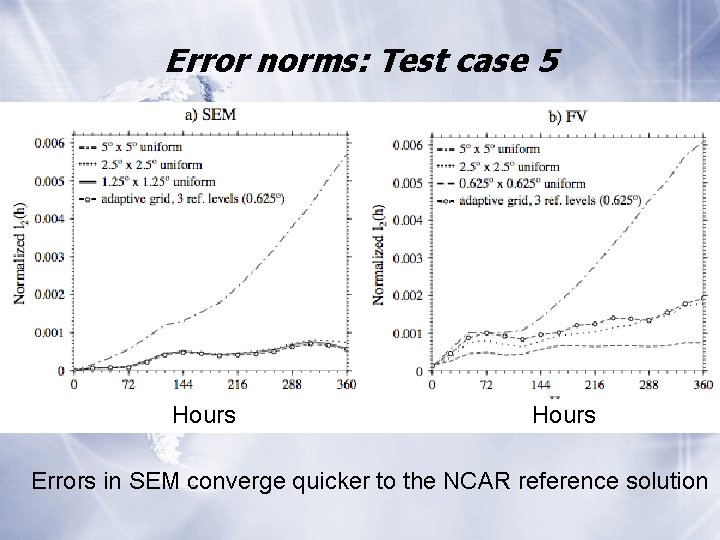
Error norms: Test case 5 Hours Errors in SEM converge quicker to the NCAR reference solution
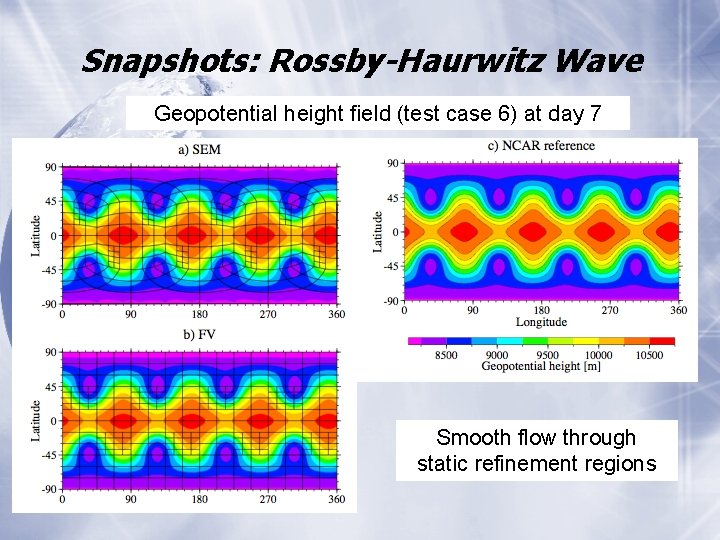
Snapshots: Rossby-Haurwitz Wave Geopotential height field (test case 6) at day 7 Smooth flow through static refinement regions

Alternative AMR: Unstructured Triangular Grid Hurricane Floyd (1999) OMEGA model Courtesy of A. Sarma (SAIC, NC, USA) Colors indicate the wind speed

Conclusions & Outlook Both grids, cubed-sphere meshes and latitude-longitude grids, are options for AMR techniques SEM model shows lower error norms in comparison to FV: Mainly due to high-order numerical method Partly due to different AMR approach that does not need interpolations of ‘ghost cells’ in blocks But: SEM is non-monotonic and non-conservative Cubed-sphere grid has clear advantages: No convergence of the meridians, no polar filters But, GLL and GL points for numerical method in SEM are clustered along boundaries of spectral elements Future interests: Finite-volume AMR method on a cubedsphere grid
- Slides: 36