Adaptive lineare Transformationen AS 2 3 PCATransformation PCANetze

Adaptive lineare Transformationen AS 2 -3

PCA-Transformation PCA-Netze Weissen ICA-Transformation Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 -3 -

Hebb‘sches Lernen w = wi(t)-wi(t-1) = i(t) yix Iterative Hebb'sche Lernregel W = W(t)-W(t-1) = (t) yx. T W = W(1) + W(2) + W(3) + … Problem: ex. kein „Vergessen“, w Unendliches Wachstum ? ? Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 -4 -

Hebb‘sches Lernen - Ergänzungen Lösung 1: lin. Term, Abklingen der Synapsen w(t) = w(t-1) + (t) yx Iterative Hebb'sche Lernregel w(t) = w(t-1) + (t) (yx - w(t-1)) Abklingen des Gewichts -1 Diff. gleichung mit = 1/ w(t)-w(t-1) = yx - w(t-1) Erwartetes Ziel bei lin. System y = w Tx Cxx: = xx. T = 1 xy - 2 w = 1 xx. Tw - w = 1 xx. T w - 2 w = 0 Cxxw = w w* stabil? bei Fixpunkt w = w*Eigenvektor von Cxx 1 -dim Beispiel: Nein! = 1 xy - 2 wn nicht-lin. Abklingterm n>1 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 -5 -

Hebb‘sches Lernen - Ergänzungen Lösung : Normierung der Gewichte w(t) = w(t-1) + (t) yx mit |w(t)| = 1 Wie? w(t-1) + (t) yx (t) = w(t) = ____= w(t-1) + (t) yx | | Wohin konvergiert w(t) ? Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 -6 -

Lernen: beschränkte Hebbsche Regel Konvergenzziel ? wi(t) = wi(t-1) + i(t) yix Also: Hebb'sche Lernregel mit NB |w| = const. = wi(t-1) + i(t) Gradientenaufstieg = xy = xx. T w = Aw bei y = x. Tw lin. Neuron, wobei x = 0 zentriert Zielfunktion R(w) = ½ w. TAw mit Nebenbedingung |w| = const = 1 Lagrangefunktion L(w, µ) = R(w) + µ·(|w|2 – 1) Extremwert bei (w, ) = Aw = w Eigenwertgleichung + 2 w = Aw + 2 w = 0 mit : = – 2 w EV(A) mit EW = max Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 -7 -

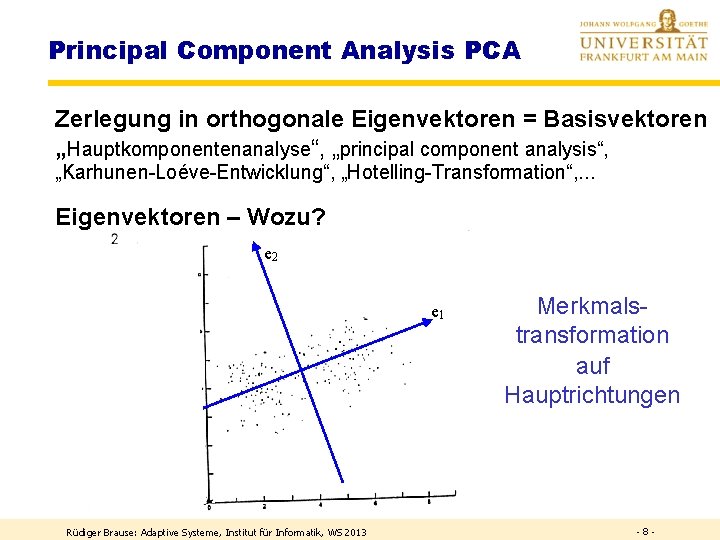
Principal Component Analysis PCA Zerlegung in orthogonale Eigenvektoren = Basisvektoren „Hauptkomponentenanalyse“, „principal component analysis“, „Karhunen-Loéve-Entwicklung“, „Hotelling-Transformation“, . . . Eigenvektoren – Wozu? e 2 e 1 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 Merkmalstransformation auf Hauptrichtungen -8 -

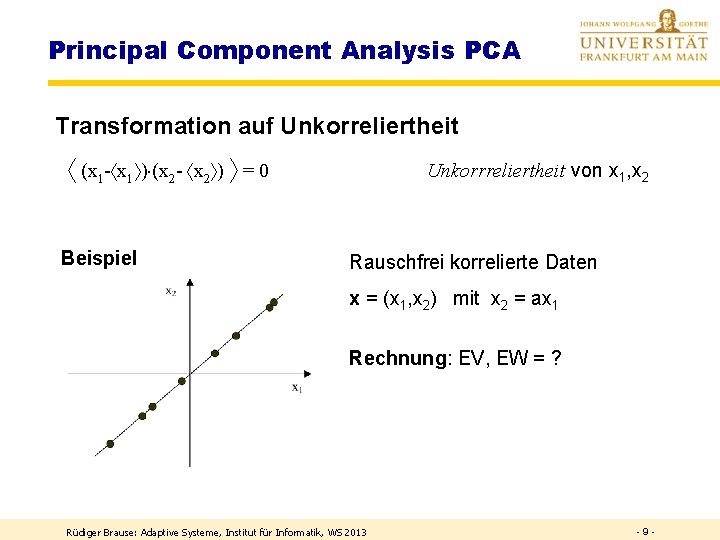
Principal Component Analysis PCA Transformation auf Unkorreliertheit (x 1 - x 1 ) (x 2 - x 2 ) = 0 Beispiel Unkorrreliertheit von x 1, x 2 Rauschfrei korrelierte Daten x = (x 1, x 2) mit x 2 = ax 1 Rechnung: EV, EW = ? Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 -9 -

Dekorrelation und Unabhängigkeit DEF dekorreliert: (yi- yi ) (yj- yj ) = yi- yi yj- yj = 0 i≠j Satz: PCA dekorreliert Daten DEF PCA: y = w. Tx mit Cxxw = w Eigenvektoren Mit PCA gilt yi‘=yi-y i , x‘= x-x yi‘yj‘ = wi. Tx‘ x‘Twj = wi. T x‘ x‘T wj = wi. TCxxwj = wi. T jwj = da ja wi. Twj = gilt. Daten sind unabhängig Daten sind dekorreliert DEF unabhängig: P(xi, xj) = P(xi)P(xj) xi, xj Zufallsvariable yiyj = = = = yi yj = 0 bei yi =0 i≠j Aber: umgekehrt gilt nicht: dekorreliert ist nicht unabhängig! Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 10 -

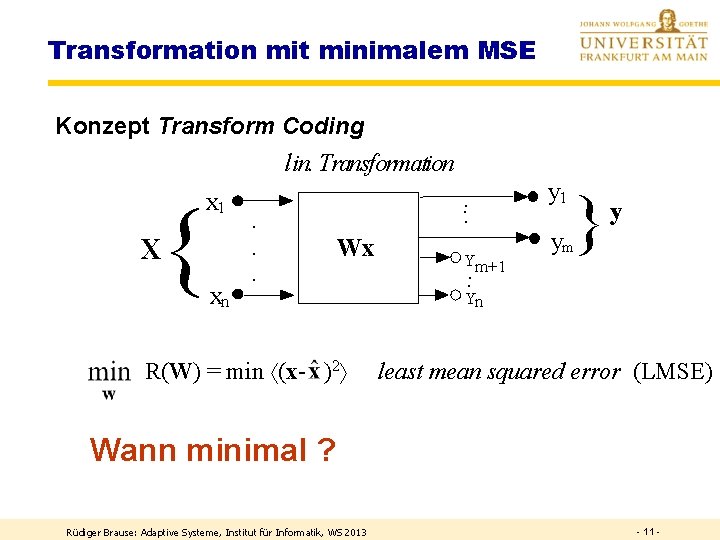
Transformation mit minimalem MSE Konzept Transform Coding lin. Transformation x 1 { X xn · · · . . . Wx R(W) = min (x- )2 Ym+1. y 1 } y ym . Yn least mean squared error (LMSE) Wann minimal ? Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 11 -

Transformation mit minimalem MSE Minimaler Rekonstruktionsfehler R(W) = min (x- )2 least mean squared error (LMSE) x= + yi = x. Twi Was ist die beste Schätzung für die Konstanten ci? min R(ci) = ? Rechnung! Anhang B Bei welchen Basisvektoren wi ist der Fehler minimal ? min R(wi) = ? Rechnung! Anhang B Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 12 -

Transformation mit minimalem MSE m Messungen f(x) x Modellierung als Gerade y = f(x) = y 0 + ax lineare Approximation Beispiel: Ökonomie Konsum y = f(Einkommen x) = Konsumsockel + a Einkommen Problem: Ergebnis hängt vom Koord. system ab Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 -

Transformation mit minimalem MSE Total Least Mean Squared Error TLMSE Minimaler mittlerer Abstand zur Gerade (Hyperebene) x u d d = x. Tw – c = g(x) w a c Hyperebene mit g(x*) = 0 = x*Tu/|u| – c = x*Tw – c Hessesche Normalform TLMSE = R(w, c) = d 2 Rechnung: Minimum des TLMSE (Kap. 3. 3. 1) Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 14 -

PCA-Transformation PCA-Netze Weissen ICA-Transformation Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 15 -

PCA Netze für geordnete Zerlegung Sanger-Methode Sanger 1988 Vollständige Zerlegung von {x} in n Eigenvektoren wobei x = 0 zentriert {x}1 = {x}, i=1 1. Suche die Richtung größter Varianz in {x}i, etwa mit der Hebb. Lernregel und |wi| =1. Dies ist wi ei. 2. Ziehe alle Anteile in der Richtung wi von {x}i ab. Wir erhalten {x}i+1. xi+1 : = xi – yiwi 3. Wenn i<n, setze i : = i+1, gehe zu 1. Diskret für stochastisches x, w: x 1 x w 1 e 1 Sanger-Netz xm-1 ··· Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 xm w. M e. M - 16 -

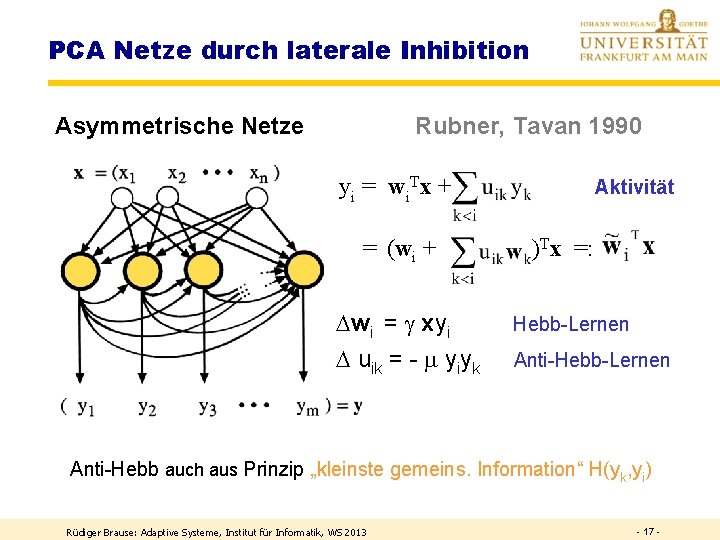
PCA Netze durch laterale Inhibition Asymmetrische Netze Rubner, Tavan 1990 yi = wi. Tx + = (wi + Aktivität )Tx =: wi = xyi Hebb-Lernen uik = - yiyk Anti-Hebb-Lernen Anti-Hebb auch aus Prinzip „kleinste gemeins. Information“ H(yk, yi) Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 17 -

PCA-Transformation PCA-Netze Weissen ICA-Transformation Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 18 -

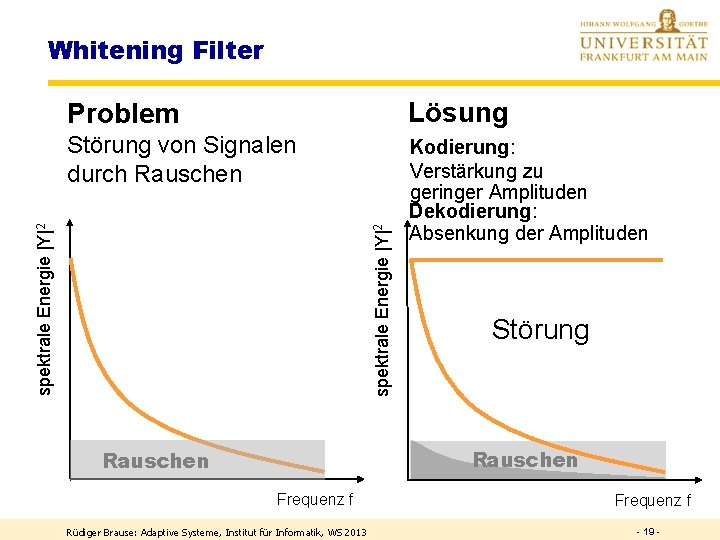
Whitening Filter Lösung Störung von Signalen durch Rauschen Kodierung: Verstärkung zu geringer Amplituden Dekodierung: Absenkung der Amplituden spektrale Energie |Y|2 Problem Störung Rauschen Frequenz f Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 Frequenz f - 19 -

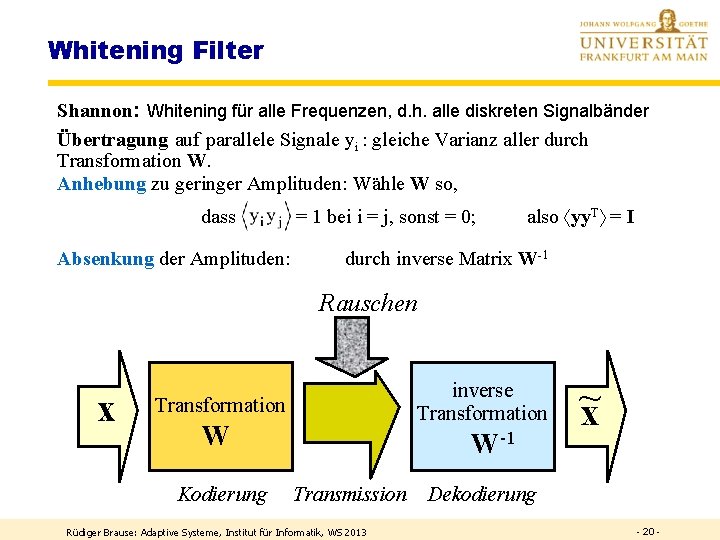
Whitening Filter Shannon: Whitening für alle Frequenzen, d. h. alle diskreten Signalbänder Übertragung auf parallele Signale yi : gleiche Varianz aller durch Transformation W. Anhebung zu geringer Amplituden: Wähle W so, dass Absenkung der Amplituden: = 1 bei i = j, sonst = 0; also yy. T = I durch inverse Matrix W-1 Rauschen x inverse Transformation W Kodierung W-1 Transmission Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 ~ x Dekodierung - 20 -

Whitening Filter Anhebung bei parallelen Signalen Wenn für die Transformation W eine orthonormale Basis M-1 = MT gewählt wird, ist das Ziel des Lernens mit I = yy. T = Wxx. TWT = W xx. T WT = WAWT auch WTI = WT (WAWT) = AWT bzw. wk = Awk Eigenvektoren wk von A mit = 1 Also: 1. 2. Signal zentrieren und PCA durchführen. Wir erhalten orthonormale Eigenvektoren ei mit Eigenwerten i. ei normieren: wi = ei / i 1/2 so dass | wi |2 =1/ i. Es ergibt sich orthogonale Transformationsmatrix W mit Zeilenvektoren wi Sie erfüllt yiyi = wi. Txx. Twi = wi. TAwi = wi. Twi i = 1 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 21 -

Whitening Filter Absenkung (Rücktransformation) W-1 = ? Wenn B = ( 1 w 1, . . . , nwn) gewählt wird, ist mit |wi|2 = i-1 mit W B = = = I, Also ist W-1 = B mit Spalten aus den um i ergänzten Zeilen von W. Also: Rücktransformation 1. Aus der PCA haben wir ei, i mit |ei|2 = 1 und so die Matrix W mit |wi|2 = i-1 2. Basis bi bilden aus W : bi = ( 1 w 1 i, 2 w 2 i, . . . , nwni) Implementierung: Orthonormalisierende Netze Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 22 -

Orthonormalisierende Netze Heuristische Methode Silva, Almeida 1991 Ziel: Projektion aij : = wi. Twj eines Basisvektors wi auf einen anderen wj vermindern wi(t) = wi(t-1) – (t) aijwj(t-1) = wi(t-1) – (t) (wi. T(t-1)wj(t-1)) wj(t-1) + (1 - yi 2 ) wi(t) Normierung Ziel: orthogonal im Datenraum: aij : = yiyj = w Alle Einflüsse wi(t) = wi(t-1) – (t) 2 ) w (t) + (1 - y wiiy. Tj(t-1) ) w (t-1) y wjw (t-1) i i j j W(t+1) = W(t) – Cyy(t) W(t) + W(t) Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 Matrixversion - 23 -

Orthonormalisierende Netze Konvergenz der Heuristischen Methode Silva, Almeida 1991 Beh: Cyy I mit Cyy = yy. T = W xx. T WT= WCxx. WT Bew: Einsetzen der Matrixversion W(t+1) = W(t) - Cyy(t) W(t) + W(t) Cyy(t+1) = 2 Cyy 3 -2 (1+ )Cyy 2+(1+ )2 Cyy Darstellung im Eigenvektorraum Cyy ei = ei i Cyy. E = E Cyy = E ET ändert die Eigenvektoren nicht, sondern nur die Eigenwerte zu (t+1) = 2 3 - 2 (1+ ) 2 + (1+ )2 Fixpunktgleichung (t+1) Stabile, labile Fixpunkte? Konvergenz 1 Cyy I *=1 (t) q. e. d. Ex. keine Zielfunktion ! Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 2009 - 24 -

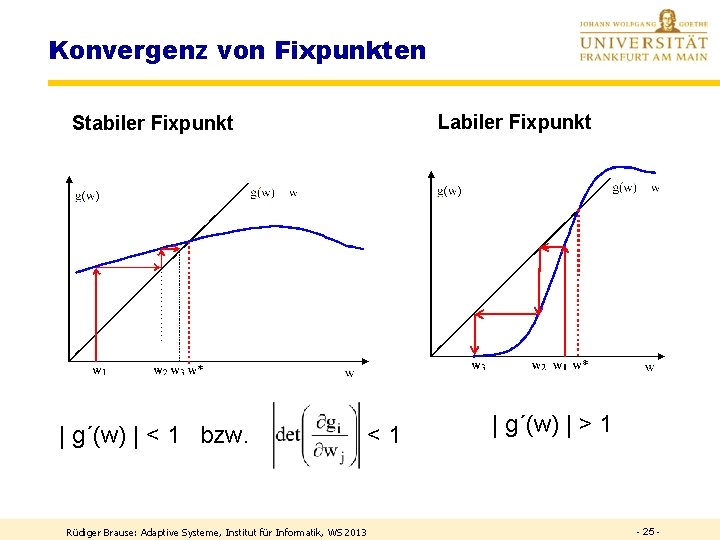
Konvergenz von Fixpunkten Labiler Fixpunkt Stabiler Fixpunkt | g´(w) | < 1 bzw. <1 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 | g´(w) | > 1 - 25 -

FRAGE Sei eine Iteration mit g(x) = x 2 gegeben. Welche Fixpunkte gibt es? Welche sind stabil und welche labil? Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 26 -

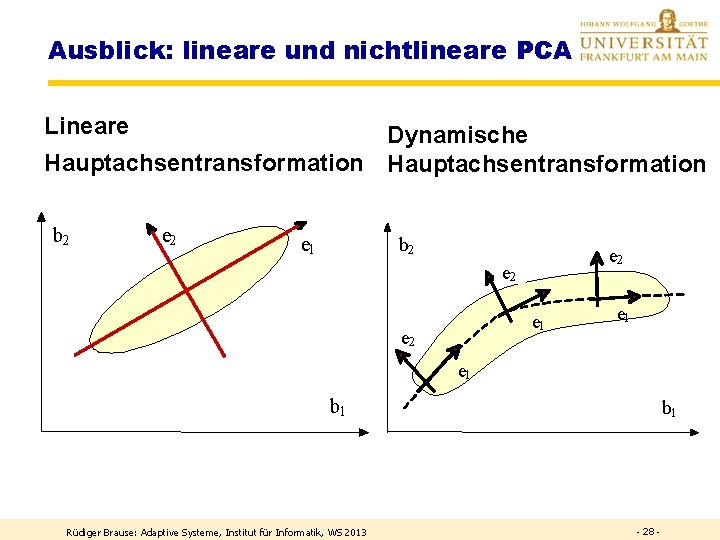
Ausblick: lineare und nichtlineare PCA Lineare Dynamische Hauptachsentransformation b 2 e 1 b 2 e 2 e 1 e 1 b 1 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 b 1 - 28 -

PCA-Transformation PCA-Netze Weissen ICA-Transformation Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 29 -

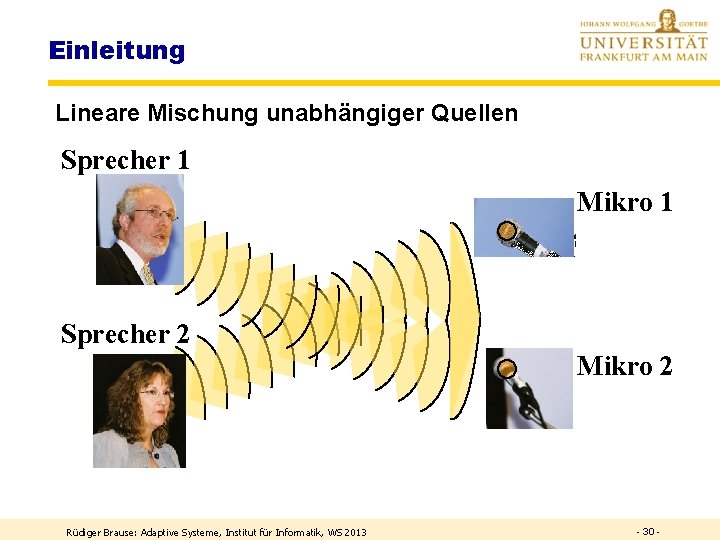
Einleitung Lineare Mischung unabhängiger Quellen Sprecher 1 Mikro 1 Sprecher 2 Mikro 2 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 30 -

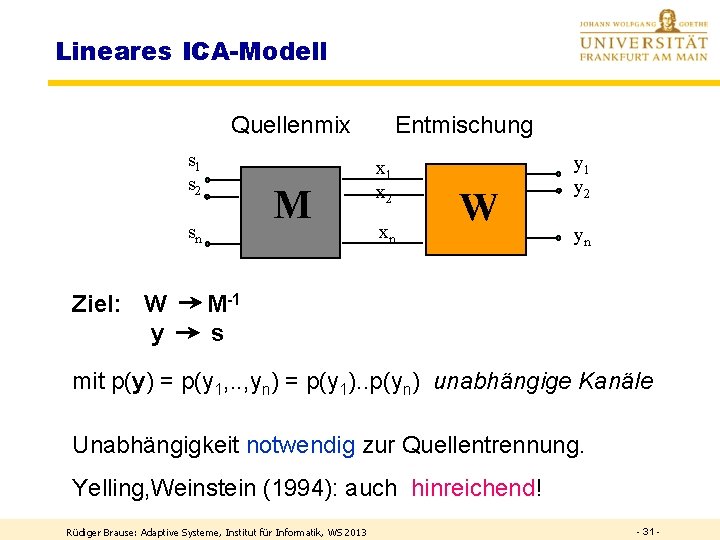
Lineares ICA-Modell Quellenmix s 1 s 2 M sn Ziel: W y Entmischung x 1 x 2 xn W y 1 y 2 yn M-1 s mit p(y) = p(y 1, . . , yn) = p(y 1). . p(yn) unabhängige Kanäle Unabhängigkeit notwendig zur Quellentrennung. Yelling, Weinstein (1994): auch hinreichend! Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 31 -

Lineare Koordinatentransformationen Beispiel: l PCA-Hauptkomponentenanalyse Richtung stärkster Varianz l ICA- Unabhängigkeitsanalyse statistische Unabhängigkeit Beispiel: x 1 = s 1+s 2, x 2 = s 2 e 2 b 2 mit s 1, s 2 zufällig uniform aus [1, +1] M=? Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 c 2 e 1 c 1 : = x 1 – x 2, c 2 : = x 2 also c 1= s 1 unabh. von c 2= s 2 b 1 , c 1 M-1 = - 32 -

ICA-Einschränkungen Quellenzahl = Mischzahl M muß regulär sein nur dann ex. M-1 Ausgabereihenfolge unbestimmt Reihenfolge in p(y 1). . p(yn) ist unwichtig => M-1 bis auf Permutation P bestimmbar: M-1 -> M-1 P Unbekannte Skalierung si : = 1 Beweis: Rechnung Kap. 3. 4 2 Gaußsche Quellen lassen sich nicht trennen max 1 Gaußsche Quelle Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 Beweis: Rechnung Kap. 3. 4 - 33 -

INFORMATIONS-METHODE Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 34 -

DEF Information I ~ n = ld(2 n) = ld (Zahl der möglichen Daten) I ~ ld(1/P) [Bit] DEF I(X) : = ln(1/P(xk)) = – ln(P(xk)) DEF H(X) : = Information k P(xk)I(xk) = I(xk) k p(x) ln p(x)-1 dx Entropie differenzielle Entropie Frage: Wieviel Information hat eine 32 -bit floating-point Zahl? DEF I(X; Y) = H(X) + H(Y) – H(X, Y) Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 Transinformation mutual information - 35 -

ICA - Algorithmen 1 a Ziel: minimale Transinformation zwischen den Ausgaben yi - x = Input. Kanäle, stoch. Variable y = Output Transinformation I(y 1; y 2) = H(y 1) + H(y 2) – H(y 1, y 2) minimal bei I(y 1; y 2) = 0 bzw. maximaler Entropie H(y 1, y 2) = H(y 1) + H(y 2) bzw. p(y 1, y 2) = p(y 1) p(y 2) stochastische Unabhängigkeit der Variablen yi W(t+1) = W(t) – I(y 1; y 2; . . ; yn) Gradientenabstieg (Amari, Young, Cichocki 1996) Entwicklung von p(y 1, y 2, . . , yn) in I(y 1; y 2; . . ; yn) nach höheren Momenten W(t+1) = W(t) – (1 -f(y)y. T)W(t) mit fi(yi) = Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 36 -

ICA - Algorithmen 1 b Ziel: maximale Transinformation - zwischen Eingabe und Ausgabe Transinformation (Bell, Sejnowski 1995) I(X; Y) = H(Y) – H(Y|X) aus Def. H(Y|X) ist konstant im determinist. System Maximimierung von I(X; Y) durch Maximierung von H(Y) R(w) : = H(Y) Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 37 -

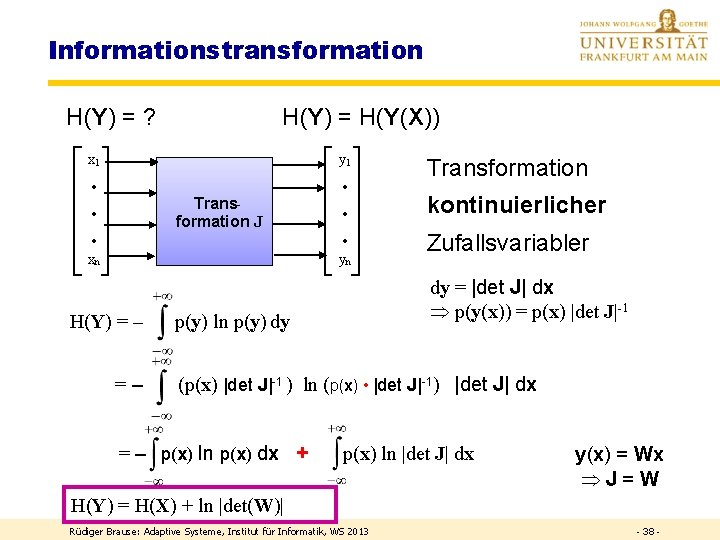
Informationstransformation H(Y) = ? H(Y) = H(Y(X)) x 1 y 1 · · Transformation J · · xn yn H(Y) = – =– Transformation kontinuierlicher Zufallsvariabler dy = |det J| dx p(y(x)) = p(x) |det J|-1 p(y) ln p(y) dy (p(x) |det J|-1 ) ln (p(x) • |det J|-1) |det J| dx = – p(x) ln p(x) dx + p(x) ln |det J| dx y(x) = Wx J=W H(Y) = H(X) + ln |det(W)| Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 38 -

ICA - Algorithmen 1 b Ziel: maximale Transinformation - zwischen Eingabe und Ausgabe R(w) = H(X) + (Bell, Sejnowski 1995) p(x) ln |det J|dx Mit nicht-lin. Ausgabe y, mit J = z. B. y = tanh(z): Stoch. Gradientenaufstieg W(t+1) = W(t) + ( – 2 yx. T) Rechnung: 1 -dim Fall (Kap. 3. 4. 1) „Natürl. “Gradient Amari 1985 = W = (t) WTW = (I – 2 yz. T)W W(t+1) = W(t) + (I – 2 yz. T)W Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 39 -

Frage Wodurch unterscheiden sich die beiden Algorithmen hauptsächlich? a) garnicht b) im Ergebnis c) in den Zielfunktionen d) in den Zielen e) in der Konvergenzgeschwindigkeit Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 40 -

KURTOSIS-METHODE Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 41 -

Statist. Momente und Kurtosis Momente einer Zufallsvariablen x : ai= x i, z. B. a 1 = x Zentrale Momente einer Zufallsvariablen x: mk= (x-a 1)k , z. B. m 2 = (x-a 1)2 Wölbungsmaß Kurtosis: Mittelwert Varianz kurt(x) = [ (x-a 1) 4 -3 m 22]/m 22 Supergaussian: Kurtosis > 0 Gaussian: Kurtosis = 0 Subgaussian: Kurtosis < 0 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 42 -

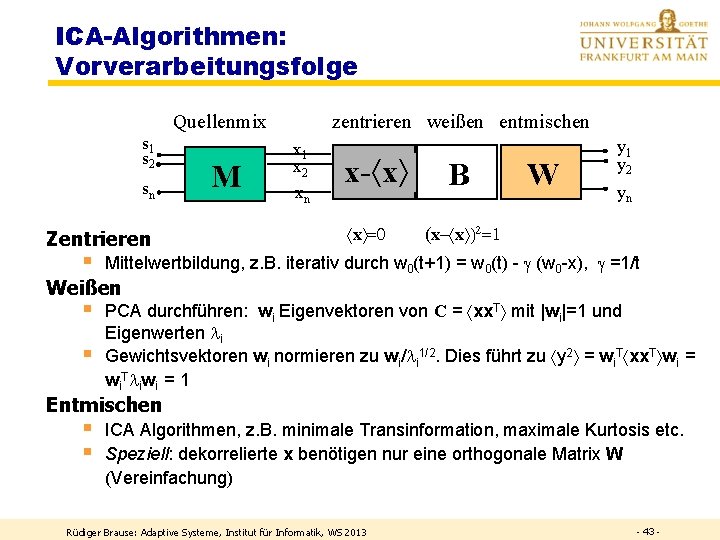
ICA-Algorithmen: Vorverarbeitungsfolge Quellenmix s 1 s 2 sn Zentrieren § M zentrieren weißen entmischen x 1 x 2 xn x- x x =0 B W y 1 y 2 yn (x- x )2=1 Mittelwertbildung, z. B. iterativ durch w 0(t+1) = w 0(t) - (w 0 -x), =1/t Weißen § § PCA durchführen: wi Eigenvektoren von C = xx. T mit |wi|=1 und Eigenwerten i Gewichtsvektoren wi normieren zu wi/ i 1/2. Dies führt zu y 2 = wi. T xx. T wi = wi. T iwi = 1 Entmischen § § ICA Algorithmen, z. B. minimale Transinformation, maximale Kurtosis etc. Speziell: dekorrelierte x benötigen nur eine orthogonale Matrix W (Vereinfachung) Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 43 -

ICA – Algorithmen 2 Ziel: extremale Kurtosis (Delfosse, Loubaton 1995) Extrema bei sj = unabh. Komp, und zj = +/-1 kurt (y) = kurt (w. Tv) = kurt(w. TMs) = kurt (z. Ts) = Quellenmix zentrieren weißen s 1 entmischen s 2 sn M Matrix Z Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 v 1 v 2 vn W y 1 y 2 yn (vi- vi )2=1 vi =0 - 44 -

ICA – Algorithmen 2 Ziel: extremale Kurtosis bei y = w. Tv R(w) = (w. Tv)4 – 3 (w. Tv)2 2 = minw w(t+1) = w(t) + grad R(w) = w(t) + 4 ( (w. Tv)3 v – 3|w|2 w) Bei |w| = 1 ist die Richtung gegeben durch w(t+1) = a( (w. Tv)3 v – bw) Lernalgorithmus für einzelnes Neuron (Hyvarinen, Oja 1996) w(t+1) = (w. Tv)3 v – 3 w Fixpunktalgorithmus mit |w| = 1 Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 45 -

ICA – Algorithmen 2 Sequentielle Extraktion aller Komponenten Gegeben: Trainingsmenge {v(0)} w 1(t+1) = (w 1 Tv)3 v – 3 w 1 Konvergenz zum 1. ICA-Vektor. Dann neue Trainingsmenge durch v(1) mit |w 1| = 1 = v(0) – w 1 y 1 w 2(t+1) = (w 2 Tv)3 v – 3 w 2 mit |w 2| = 1 Konvergenz zum 2. ICA-Vektor, usw. Schnellere Konvergenz: Orthogonalisierung wi(t+1) = wi(t) Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 (wi wj) wj j < i - 46 -

Frage Wodurch ist die Reihenfolge der sequentiell ermittelten ICA-Komponenten bestimmt? Wodurch ist der Index i bei y 1, …, yi, …yn festgelegt? ANTWORT: Durch die Größe der Kurtosis der i-ten Komponente. Als Erstes wird die Komponente mit der größten Kurtosis ermittelt. Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 47 -

ICA-Anwendung: Audioanalyse Mischung entmischte Quellen Mix 1 speaker Mix 2 singer Mix 3 violin Mix 4 orchestra Rüdiger Brause: Adaptive Systeme, Institut für Informatik, WS 2013 - 48 -