Adaptive Learning Networks Adaptive Filters V 1 V

Adaptive / Learning Networks

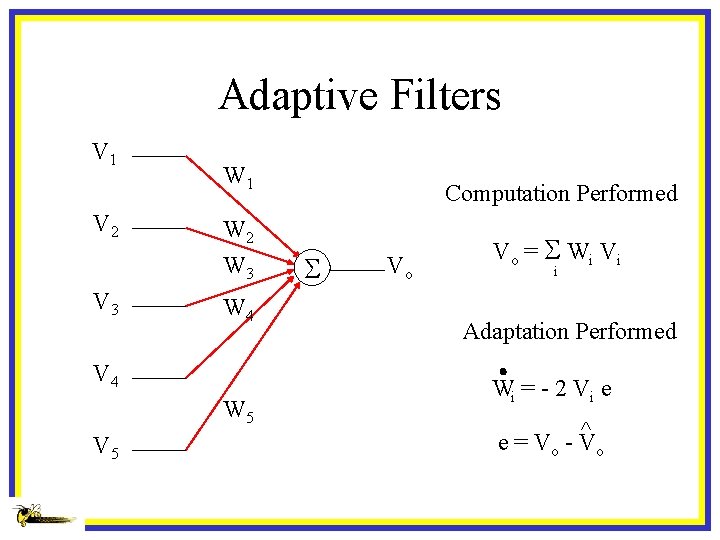
Adaptive Filters V 1 V 2 W 1 W 2 W 3 V 3 W 4 V 4 W 5 V 5 Computation Performed S Vo Vo = S W i Vi i Adaptation Performed Wi = - 2 Vi e ^ e = Vo - V o

Developing Silicon Synapses 1. Must store the weights in a nonvolatile manner 2. Must compute a product of the stored weight and the input signal ( W * X ) 3. Must take minimal silicon area ( most of the area taken by synapses --- want as many as possible ) 4. Must consume minimal power --- subthreshold ( total power = indiviual element * # of synapses) 5. Must update the weight value based at least upon an outer-product learning rule

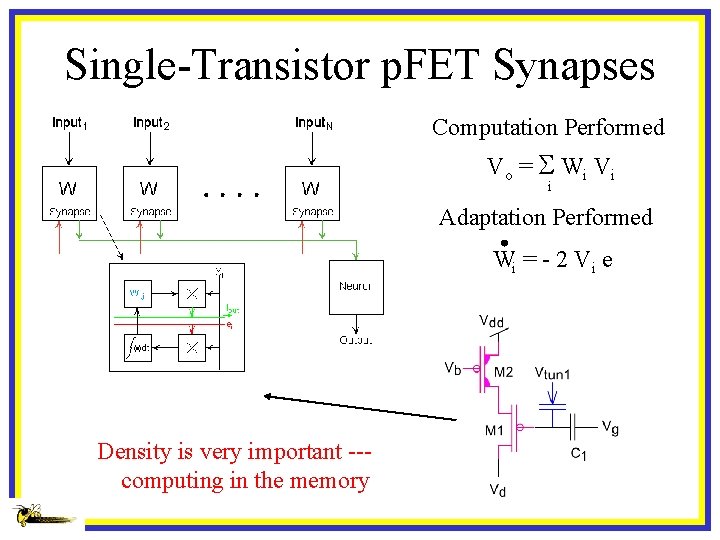
Single-Transistor p. FET Synapses Computation Performed Vo = S W i Vi i Adaptation Performed Wi = - 2 Vi e Density is very important --computing in the memory

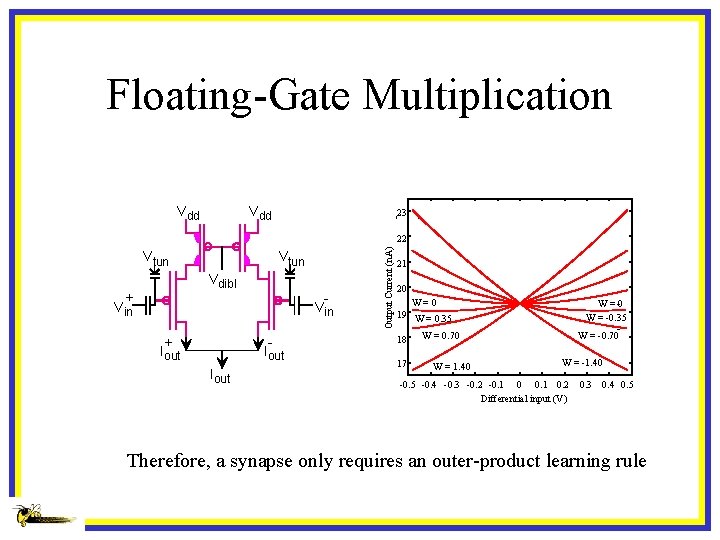
Floating-Gate Multiplication Vdd 23 Vtun Vdibl + Vin + Iout Output Current (n. A) 22 21 20 W=0 19 W = 0. 35 18 17 W=0 W = -0. 35 W = -0. 70 W = 1. 40 W = -1. 40 -0. 5 -0. 4 -0. 3 -0. 2 -0. 1 0. 2 Differential input (V) 0. 3 0. 4 0. 5 Therefore, a synapse only requires an outer-product learning rule

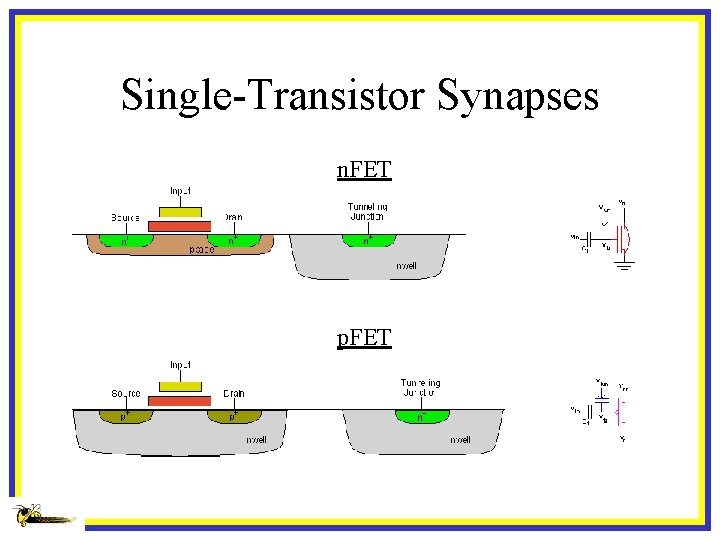
Single-Transistor Synapses n. FET p. FET

Adaptive Filters V 1 Vo 1 V 2 Vo 2 o V 3 Vo 3 V 4 Vo 4 V 5

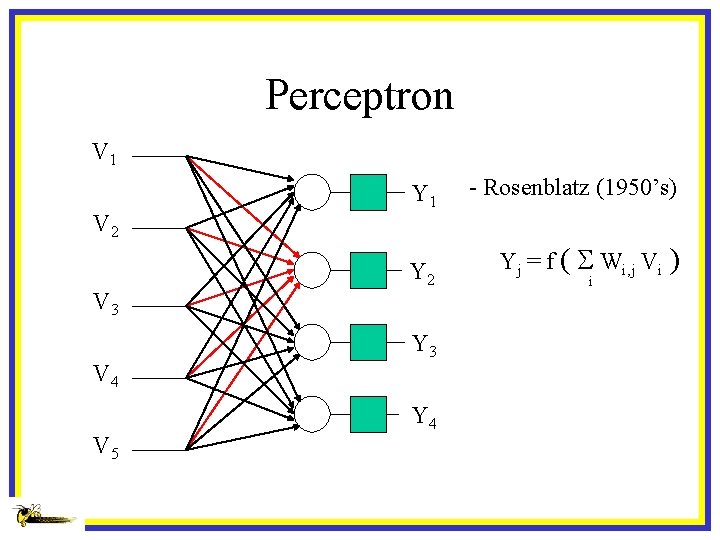
Perceptron V 1 V 2 V 3 V 4 V 5 Vo 1 Y 1 - Rosenblatz (1950’s) Vo 2 o. Y 2 Yj = f ( S Wi, j Vi ) Vo 3 Y 3 Vo 4 Y 4 i

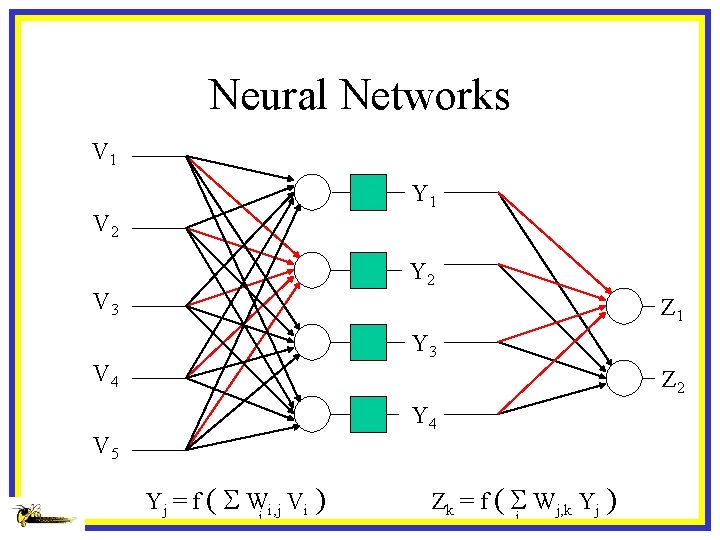
Neural Networks V 1 Y 1 V 2 Y 2 V 3 Z 1 Y 3 V 4 Z 2 Y 4 V 5 Yj = f ( S Wi, j Vi ) i Zk = f ( S Wj, k Yj ) j

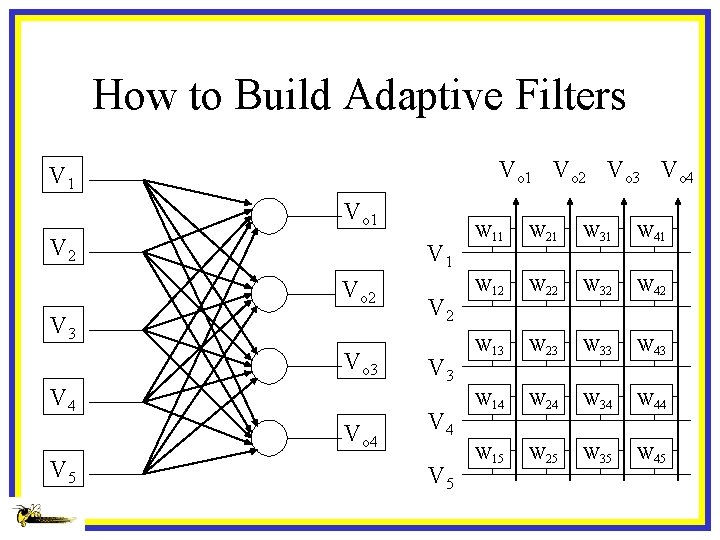
How to Build Adaptive Filters Vo 1 Vo 2 Vo 3 Vo 4 V 1 Vo 1 V 2 V 1 Vo 2 o V 3 Vo 3 V 4 Vo 4 V 5 V 2 V 3 V 4 V 5 W 11 W 21 W 31 W 41 W 12 W 22 W 32 W 42 W 13 W 23 W 33 W 43 W 14 W 24 W 34 W 44 W 15 W 25 W 35 W 45

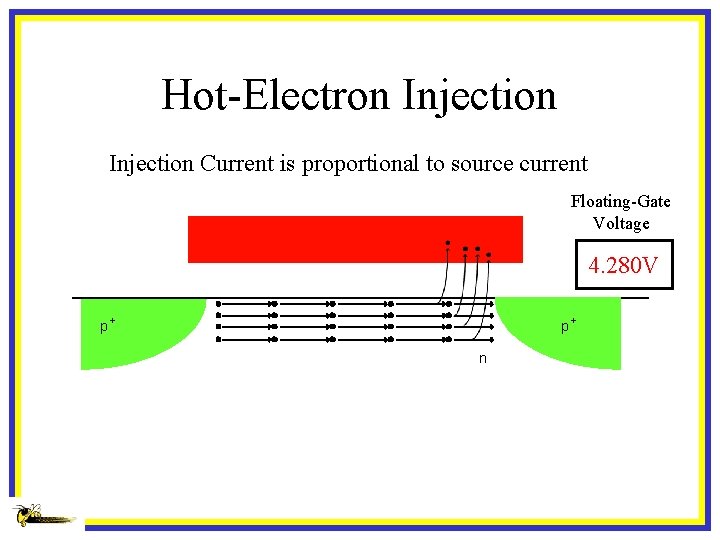
Hot-Electron Injection Current is proportional to source current Floating-Gate Voltage 4. 319 V 4. 351 V 4. 280 V 4. 352 V p+ p+ n

One Single-Transistor p. FET Circuit

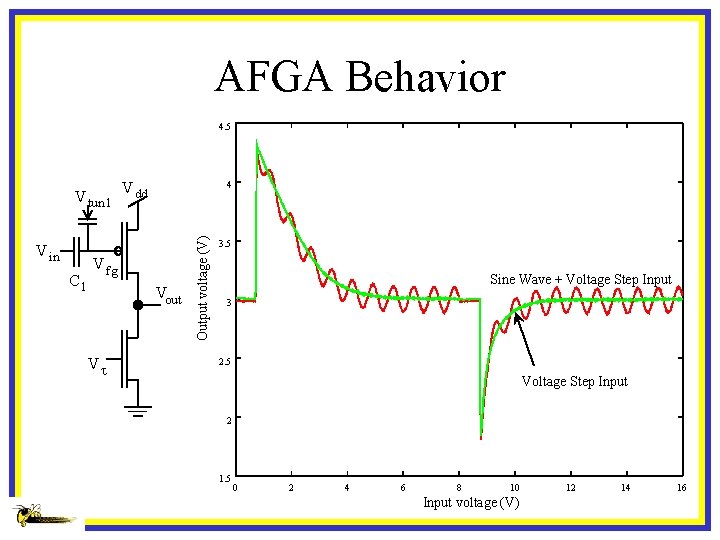
AFGA Behavior 4. 5 V in C 1 V dd 4 V fg Vout Vt Output voltage (V) V tun 1 3. 5 Sine Wave + Voltage Step Input 3 2. 5 Voltage Step Input 2 1. 5 0 2 4 6 8 10 Input voltage (V) 12 14 16

Circuit Dynamics Employing one Single-Transistor Synapse

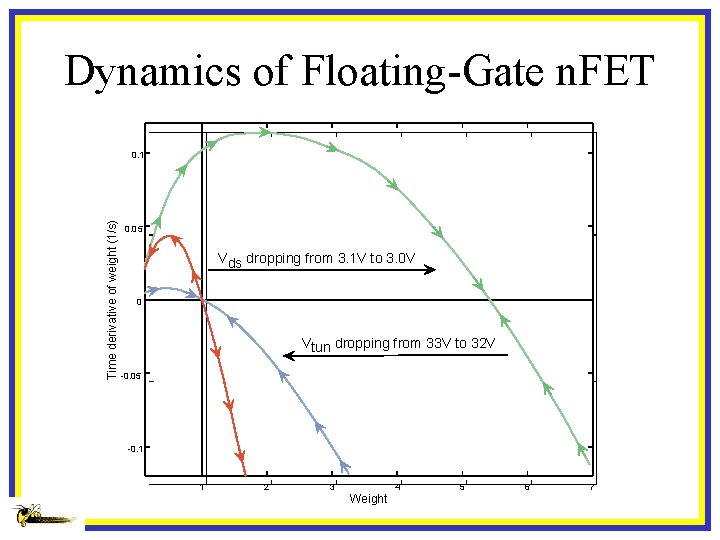
Dynamics of Floating-Gate n. FET Time derivative of weight (1/s) 0. 1 0. 05 Vds dropping from 3. 1 V to 3. 0 V 0 Vtun dropping from 33 V to 32 V -0. 05 -0. 1 1 2 3 4 Weight 5 6 7

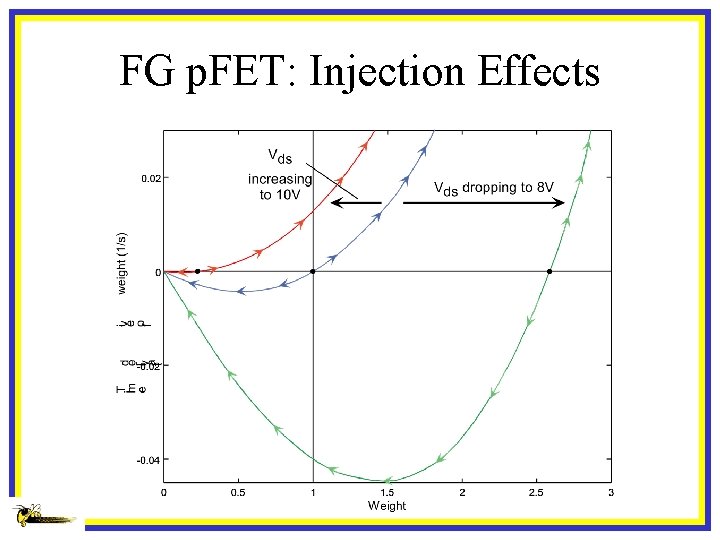
FG p. FET: Injection Effects

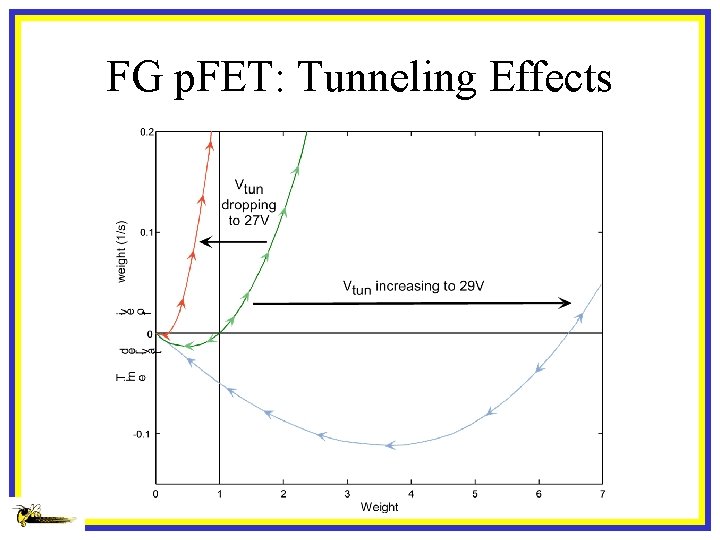
FG p. FET: Tunneling Effects

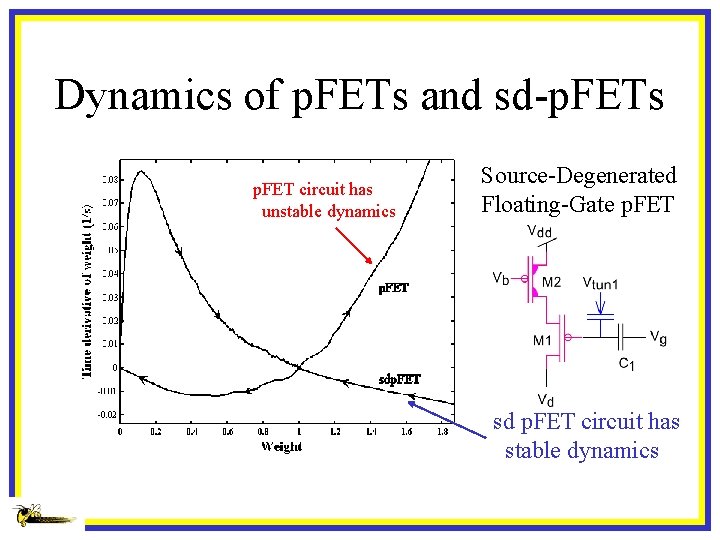
Dynamics of p. FETs and sd-p. FETs p. FET circuit has unstable dynamics Source-Degenerated Floating-Gate p. FET sd p. FET circuit has stable dynamics

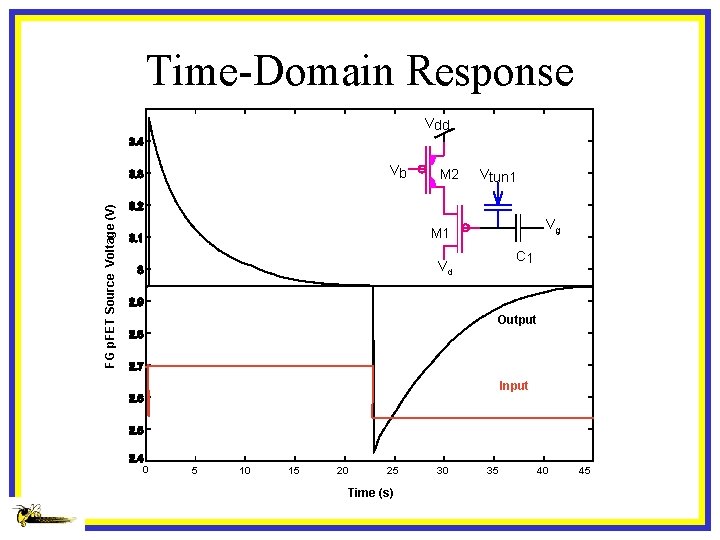
Time-Domain Response Vdd FG p. FET Source Voltage (V) Vb M 2 Vtun 1 Vg M 1 C 1 Vd Output Input 0 5 10 15 20 25 Time (s) 30 35 40 45

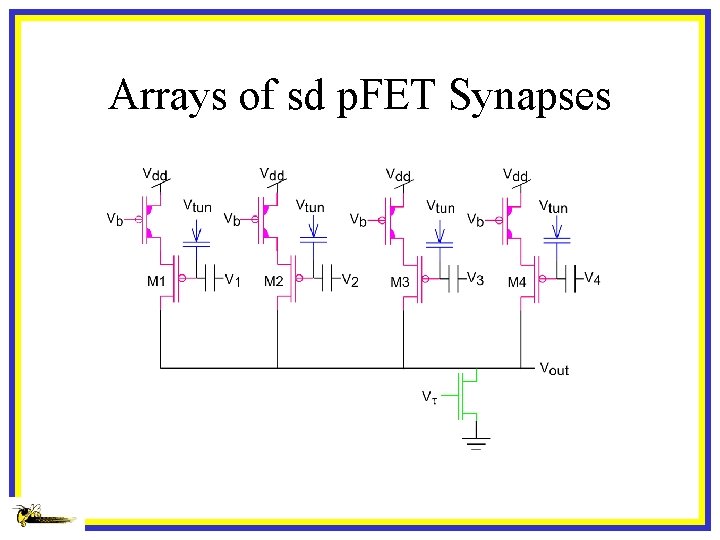
Arrays of sd p. FET Synapses

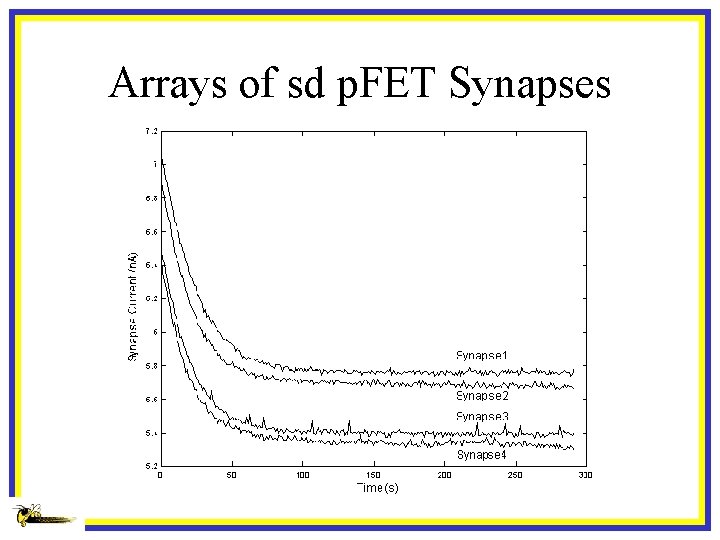
Arrays of sd p. FET Synapses

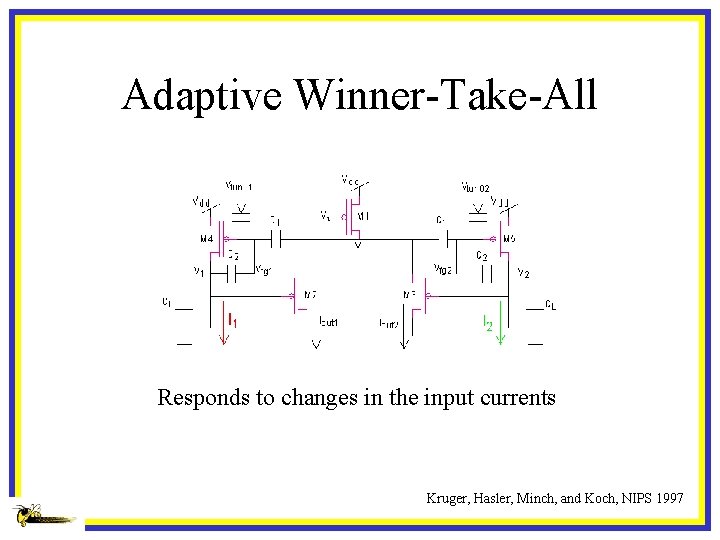
Adaptive Winner-Take-All Responds to changes in the input currents Kruger, Hasler, Minch, and Koch, NIPS 1997

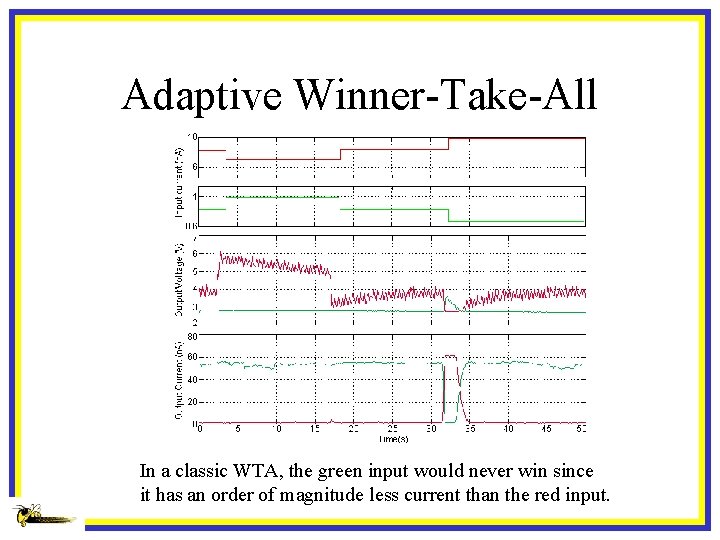
Adaptive Winner-Take-All In a classic WTA, the green input would never win since it has an order of magnitude less current than the red input.

Current Summary • Floating-Gate circuits naturally work in capacitive-based circuits • AFGAs are an important building block in classical and neuromorphic circuits • Circuits based on these concepts “resist change”

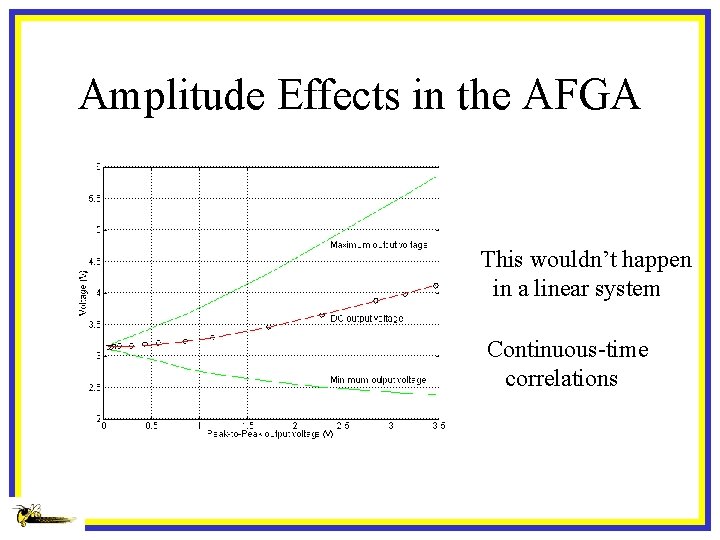
Amplitude Effects in the AFGA This wouldn’t happen in a linear system Continuous-time correlations

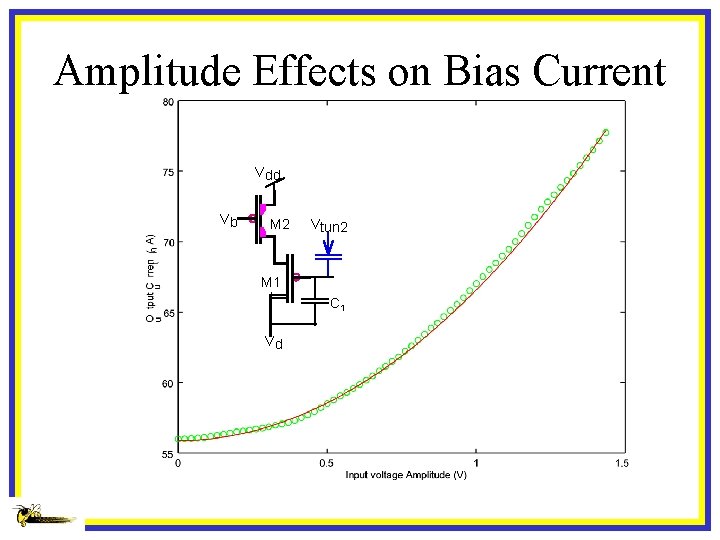
Amplitude Effects on Bias Current Vdd Vb M 2 Vtun 2 M 1 C 1 Vd

Gain-Adapting AFGA Adaptation Two floating-gates Two circuit parameters: 1. Output Offset 2. Bandpass Gain Adaptive Conductance AFGA

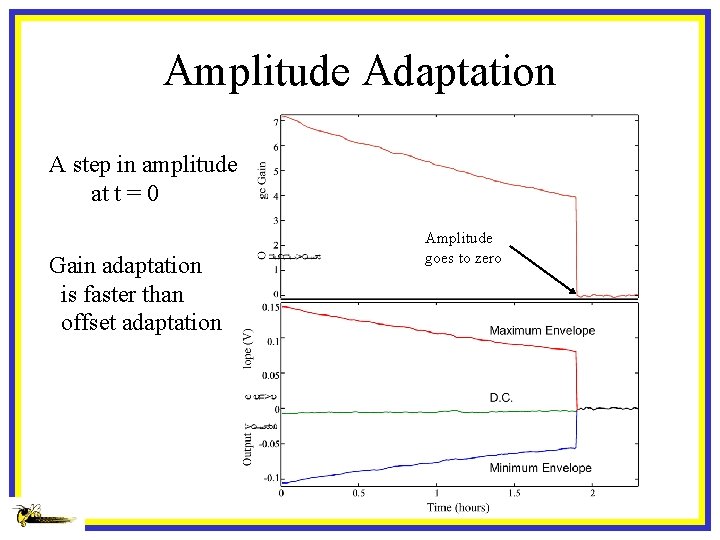
Amplitude Adaptation A step in amplitude at t = 0 Gain adaptation is faster than offset adaptation Amplitude goes to zero

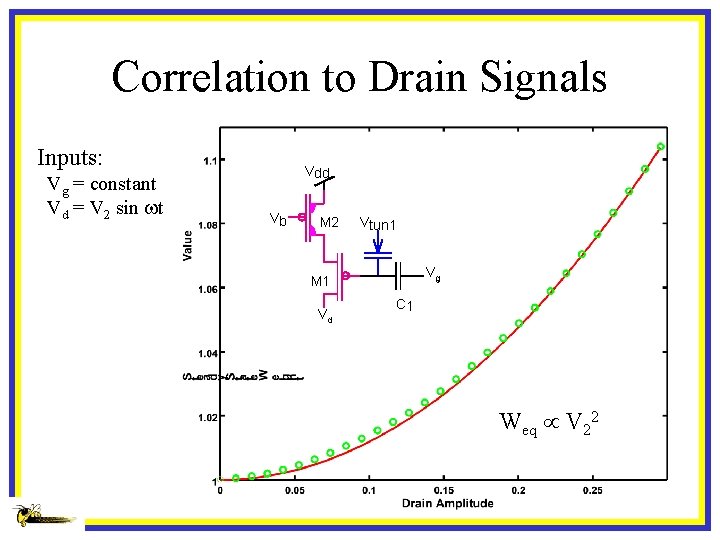
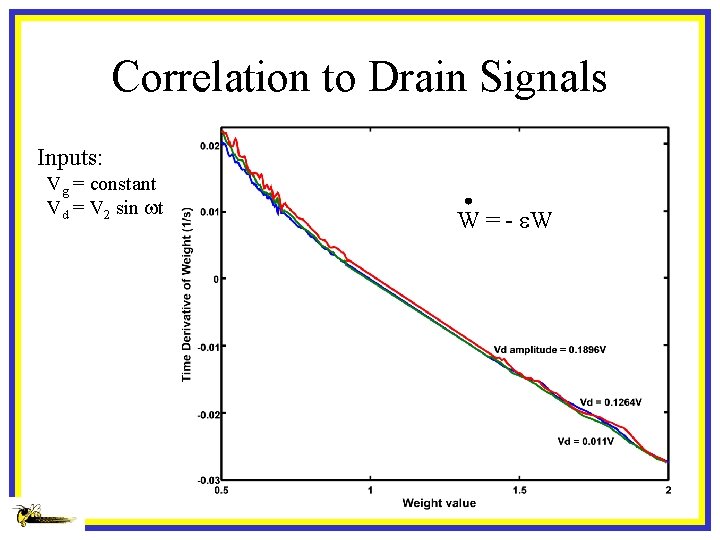
Correlation to Drain Signals Inputs: Vg = constant Vd = V 2 sin wt Vdd Vb M 2 Vtun 1 Vg M 1 Vd C 1 Weq V 22

Correlation to Drain Signals Inputs: Vg = constant Vd = V 2 sin wt W = - e. W

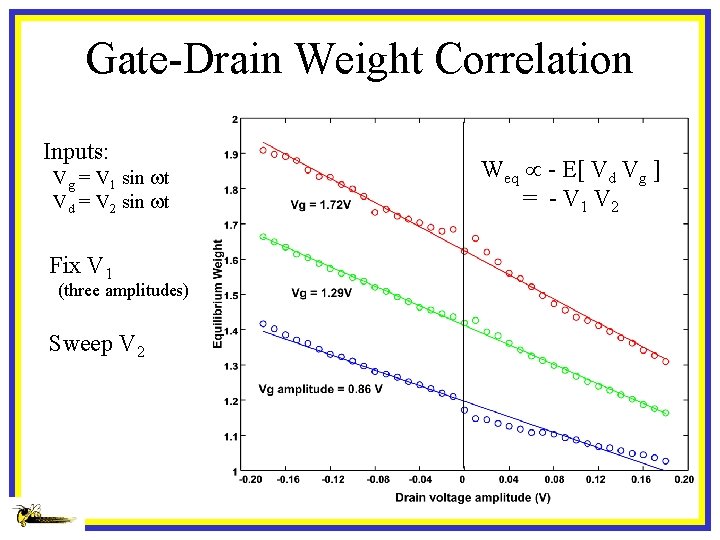
Gate-Drain Weight Correlation Inputs: Vg = V 1 sin wt Vd = V 2 sin wt Fix V 1 (three amplitudes) Sweep V 2 Weq - E[ Vd Vg ] = - V 1 V 2

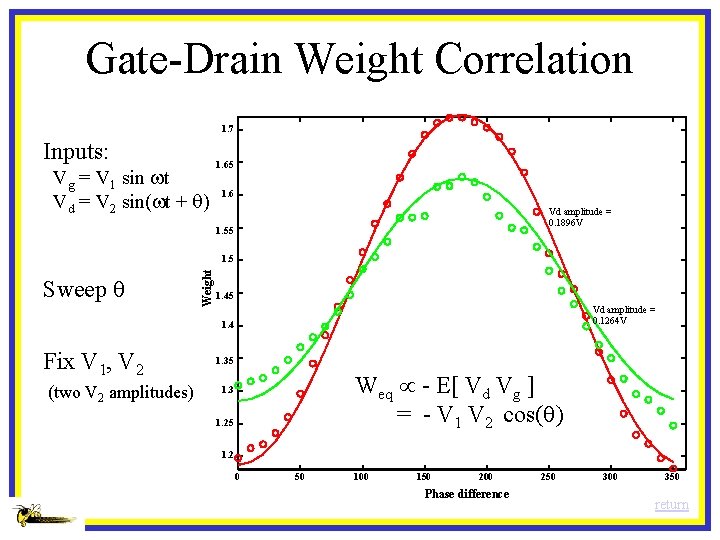
Gate-Drain Weight Correlation 1. 7 Inputs: Vg = V 1 sin wt Vd = V 2 sin(wt + q) 1. 65 1. 6 Vd amplitude = 0. 1896 V 1. 55 Sweep q Weight 1. 5 1. 45 Vd amplitude = 0. 1264 V 1. 4 Fix V 1, V 2 (two V 2 amplitudes) 1. 35 Weq - E[ Vd Vg ] = - V 1 V 2 cos(q) 1. 3 1. 25 1. 2 0 50 100 150 200 Phase difference 250 300 350 return

Drain-Gate Dynamic Equation W = 1 -h. E[Vg Vd] - e. W

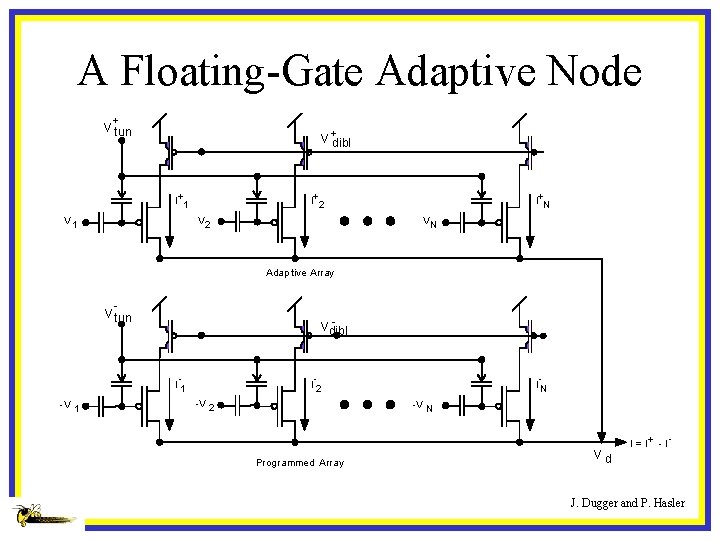
A Floating-Gate Adaptive Node + V tun V +dibl I+1 I+2 V 1 I+N VN Adap tive Array V tun Vdibl I 1 -V 1 I 2 -V 2 IN -V N Progr ammed Array Vd I = I+ - I J. Dugger and P. Hasler

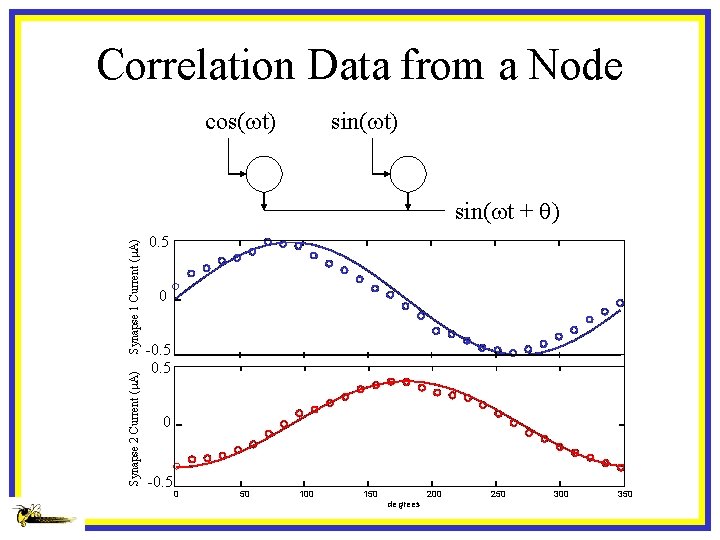
Correlation Data from a Node cos(wt) sin(wt) Synapse 2 Current (m. A) Synapse 1 Current (m. A) sin(wt + q) 0. 5 0 -0. 5 0 50 100 150 degrees 200 250 300 350

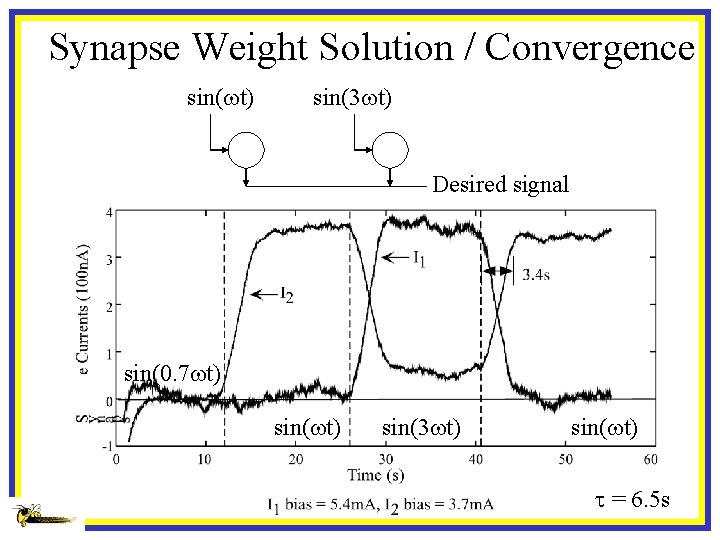
Synapse Weight Solution / Convergence sin(wt) sin(3 wt) Desired signal sin(0. 7 wt) sin(3 wt) sin(wt) t = 6. 5 s

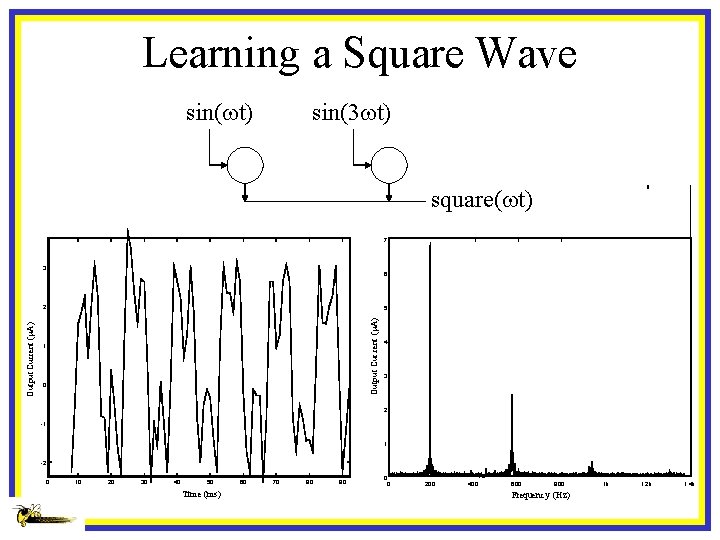
Learning a Square Wave sin(wt) sin(3 wt) square(wt) 7 3 6 5 Outpu t Cur rent (m. A) Output Current (m. A) 2 1 0 4 3 2 -1 1 -2 0 10 20 30 40 50 Time (ms) 60 70 80 90 0 0 200 400 600 800 Frequenc y (Hz) 1 k 1. 2 k 1. 4 k