Activity Introduction 1 Hydration Ions do not act


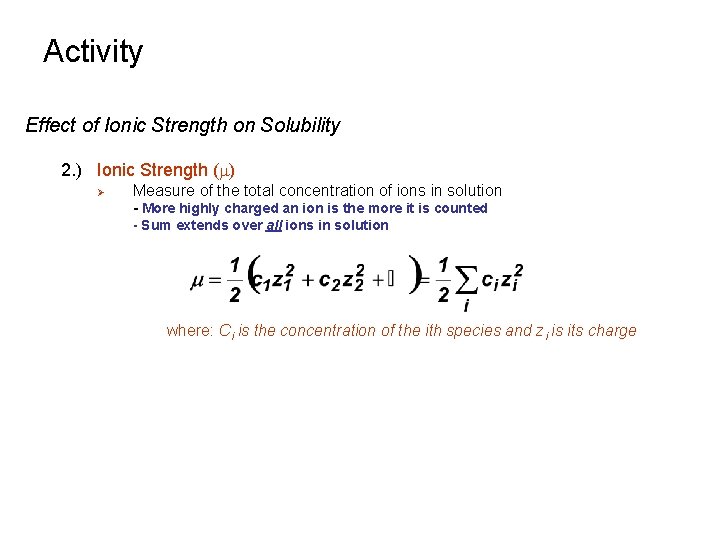





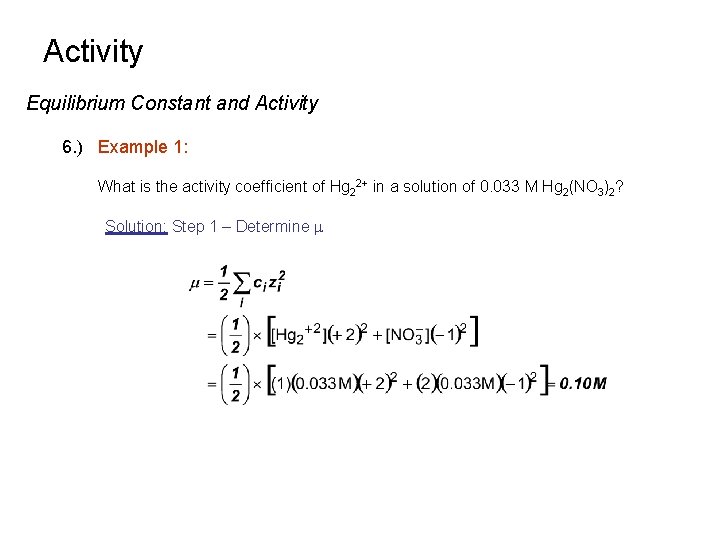






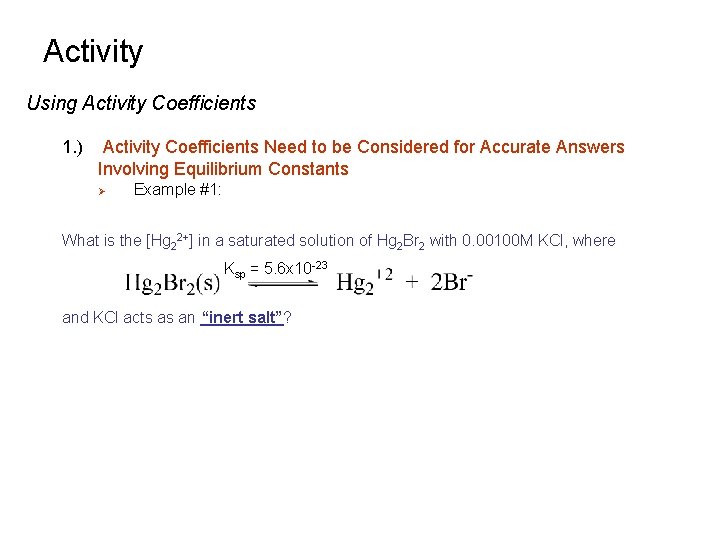


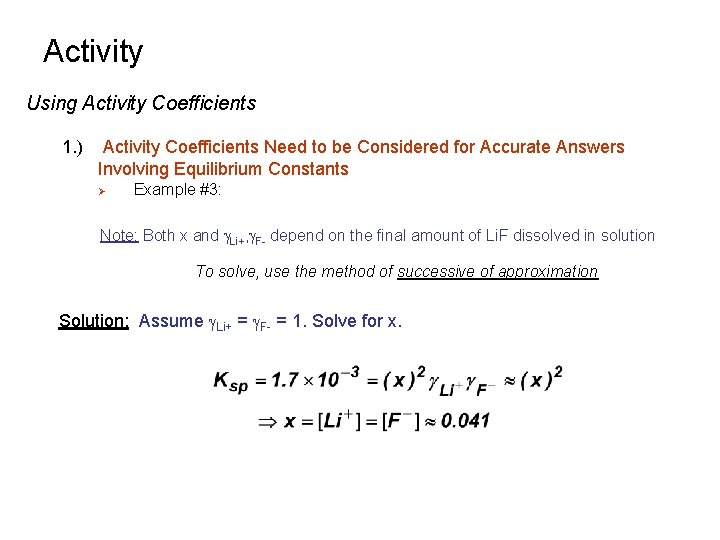





























- Slides: 57

Activity Introduction 1. ) Hydration Ø Ø Ions do not act as independent particles in solvent (water) Surrounded by a shell of solvent molecules Oxygen has a partial negative charge and hydrogen partial positive charge Oxygen binds cations Hydrogen binds anions

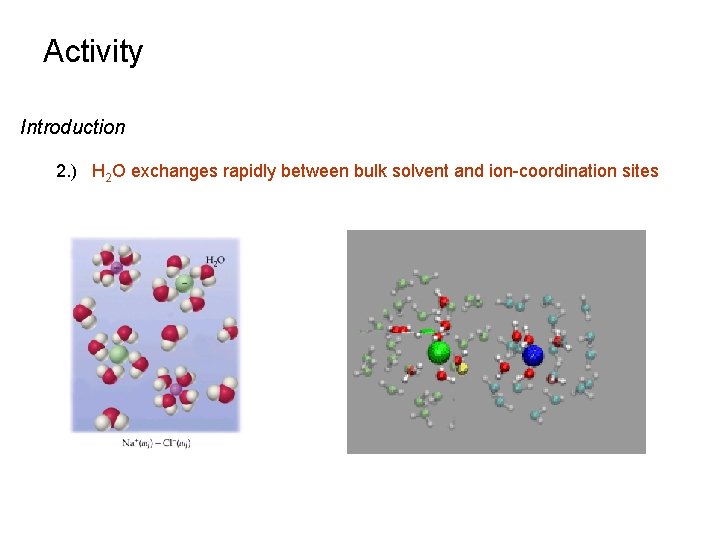
Activity Introduction 2. ) H 2 O exchanges rapidly between bulk solvent and ion-coordination sites

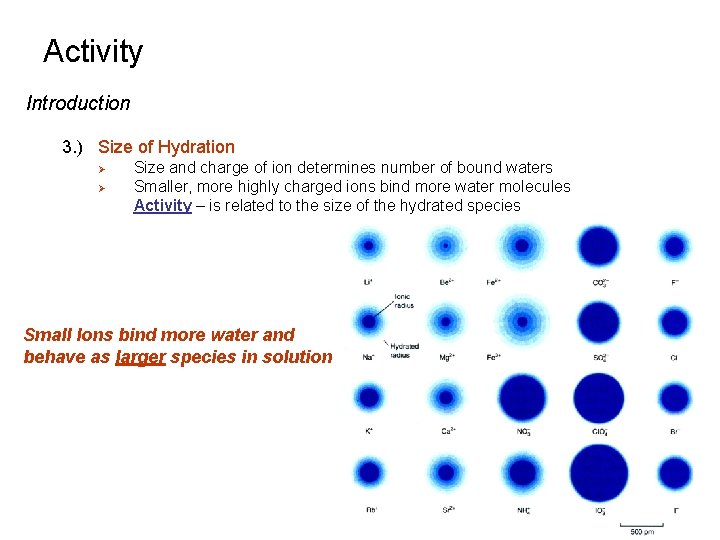
Activity Introduction 3. ) Size of Hydration Ø Ø Size and charge of ion determines number of bound waters Smaller, more highly charged ions bind more water molecules Activity – is related to the size of the hydrated species Small Ions bind more water and behave as larger species in solution

Activity Effect of Ionic Strength on Solubility 1. ) Ionic Atmosphere Ø Ø Similar in concept to hydration sphere Cation surrounded by anions and anions are surrounded by cations - Effective charge is decreased - Shields the ions and decreases attraction Ø Net charge of ionic atmosphere is less than ion - ions constantly moving in/out of ionic atmosphere Each ion-plus-atmosphere contains less net charge and there is less attraction between any particular cation and anion Each ion see less of the other ions charge and decreases the attraction

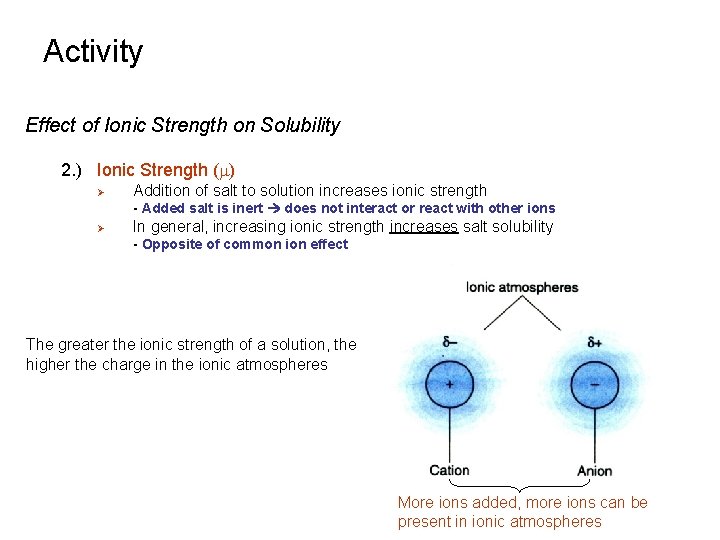
Activity Effect of Ionic Strength on Solubility 2. ) Ionic Strength (m) Ø Addition of salt to solution increases ionic strength - Added salt is inert does not interact or react with other ions Ø In general, increasing ionic strength increases salt solubility - Opposite of common ion effect The greater the ionic strength of a solution, the higher the charge in the ionic atmospheres More ions added, more ions can be present in ionic atmospheres
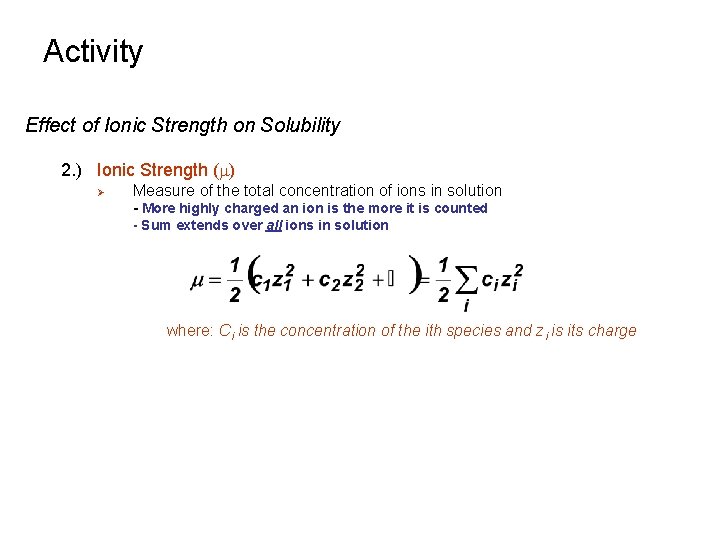
Activity Effect of Ionic Strength on Solubility 2. ) Ionic Strength (m) Ø Measure of the total concentration of ions in solution - More highly charged an ion is the more it is counted - Sum extends over all ions in solution where: Ci is the concentration of the ith species and zi is its charge

Activity Effect of Ionic Strength on Solubility 2. ) Ionic Strength (m) Ø Example: What is the ionic strength of a 0. 0087 M KOH and 0. 0002 M La(IO 3)3 solution? Assume complete dissociation and no formation of La. OH 2+

Activity Effect of Ionic Strength on Solubility 3. ) Equilibria Involving Ionic Compounds are Affected by the Presence of All Ionic Compounds in the Solution Ø Ø Knowing the ionic strength is important in determining solubility Example: Ksp = 1. 3 x 10 -18 If Hg 2(IO 3)2 is placed in pure water, up to 6. 9 x 10 -7 M will dissolve. If 0. 050 M KNO 3 is added, up to 1. 0 x 10 -6 M Hg 2(IO 3)2 will dissolve. Occurs Due to Changes in the Ionic Strength & Activity Coefficients

Activity Equilibrium Constant and Activity 1. ) Typical Form of Equilibrium Constant Ø Ø Ø However, this is not strictly correct Ratio of concentrations is not constant under all conditions Does not account for ionic strength differences 2. ) Activities, instead of concentrations should be used Ø Yields an equation for K that is truly constant where: AA, AB, AC, AD is activities of A through D

Activity Equilibrium Constant and Activity 3. ) Activities account for ionic strength effects Ø Concentrations are related to activities by an activity coefficient (g) where: AC is activity of C [C] is concentration of C g. C is activity coefficient of C 4. ) “Real” Equilibrium Constant Using Activity Coefficients

Activity Equilibrium Constant and Activity 4. ) “Real” Equilibrium Constant Using Activity Coefficients Ø g is always ≤ 1 Ø Activity coefficient measures the deviation from ideal behavior - If g =1, the behavior is ideal and typical form of equilibrium constant is used Ø Activity coefficient depends on ionic strength - Activity coefficient decrease with increasing ionic strength - Approaches one at low ionic strength Activity depends on hydrated radius (a) of the ion. This includes the ion itself and any water closely associated with it.

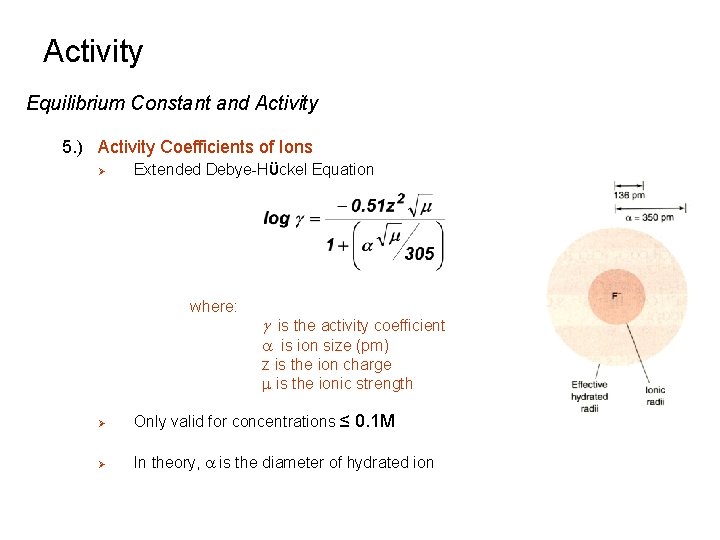
Activity Equilibrium Constant and Activity 5. ) Activity Coefficients of Ions Ø Extended Debye-Hϋckel Equation where: g is the activity coefficient a is ion size (pm) z is the ion charge m is the ionic strength Ø Only valid for concentrations ≤ 0. 1 M Ø In theory, a is the diameter of hydrated ion

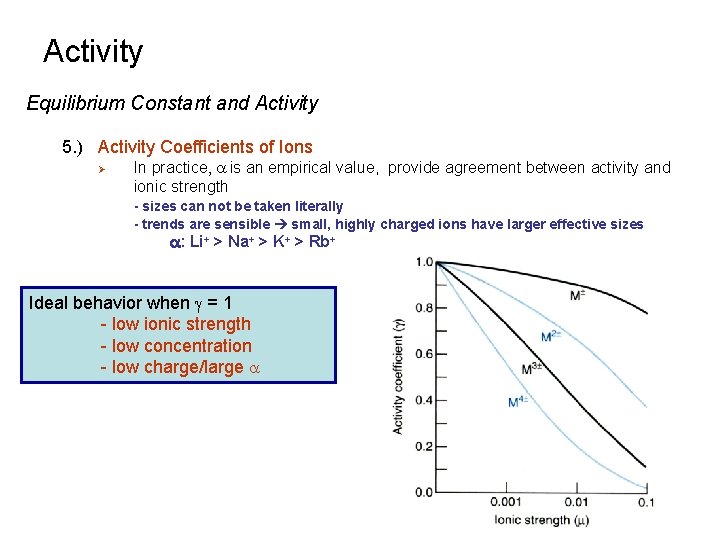
Activity Equilibrium Constant and Activity 5. ) Activity Coefficients of Ions Ø In practice, a is an empirical value, provide agreement between activity and ionic strength - sizes can not be taken literally - trends are sensible small, highly charged ions have larger effective sizes a: Li+ > Na+ > K+ > Rb+ Ideal behavior when g = 1 - low ionic strength - low concentration - low charge/large a

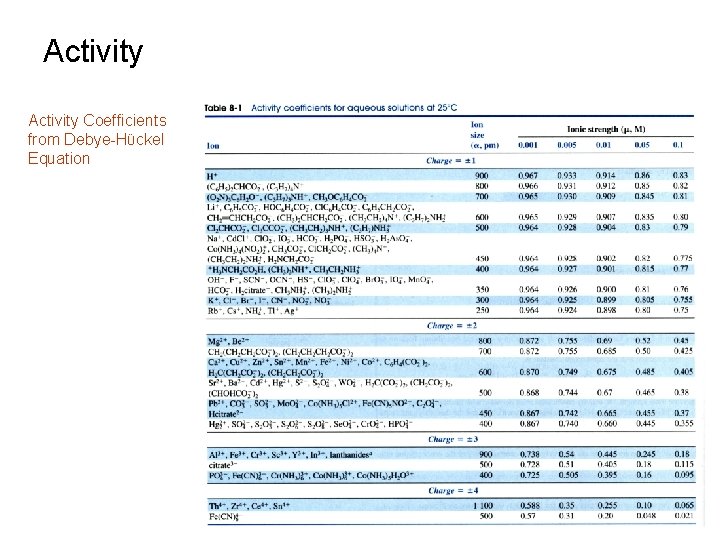
Activity Coefficients from Debye-Hϋckel Equation
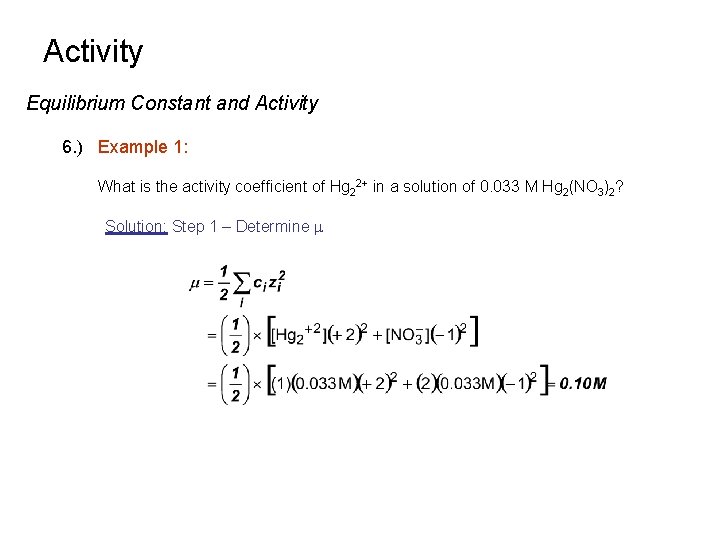
Activity Equilibrium Constant and Activity 6. ) Example 1: What is the activity coefficient of Hg 22+ in a solution of 0. 033 M Hg 2(NO 3)2? Solution: Step 1 – Determine m

Activity Equilibrium Constant and Activity 6. ) Example 1: What is the activity coefficient of Hg 22+ in a solution of 0. 033 M Hg 2(NO 3)2? Solution: Step 2 – Identify Activity Coefficient from table at corresponding ionic strength. g = 0. 355 at m = 0. 10 M

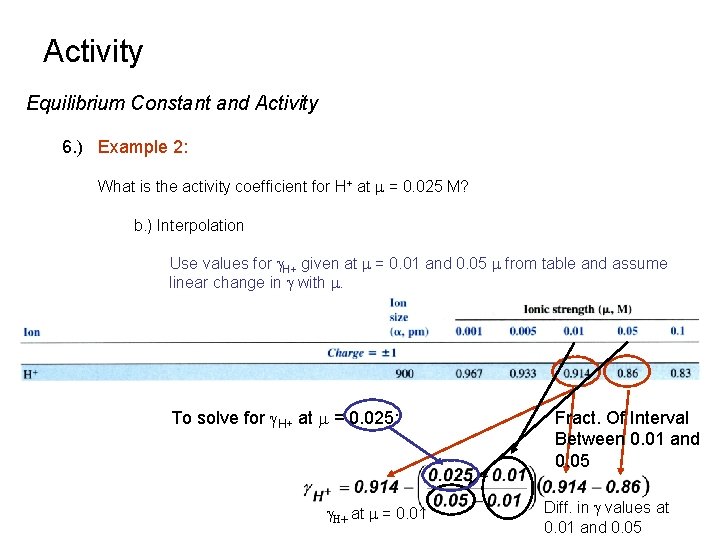
Activity Equilibrium Constant and Activity 6. ) Example 2: What is the activity coefficient for H+ at m = 0. 025 M? Note: Values for g at m = 0. 025 are not listed in the table. There are two possible ways to obtain g in this case: a. ) Direct Calculation (Debye-Hϋckel) z. H+ m a for H+ from table

Activity Equilibrium Constant and Activity 6. ) Example 2: What is the activity coefficient for H+ at m = 0. 025 M? b. ) Interpolation Use values for g. H+ given at m = 0. 01 and 0. 05 m from table and assume linear change in g with m. To solve for g. H+ at m = 0. 025: g. H+ at m = 0. 01 Fract. Of Interval Between 0. 01 and 0. 05 Diff. in g values at 0. 01 and 0. 05

Activity Equilibrium Constant and Activity 6. ) Example 2: What is the activity coefficient for H+ at m = 0. 025 M? b. ) Interpolation Use values for g. H+ given at m = 0. 01 and 0. 05 m from table and assume linear change in g with m. Note: This value is slightly different from the calculated value (0. 88) since it is only an estimate.

Activity Equilibrium Constant and Activity 7. ) Activity Coefficients of Gasses and Neutral Molecules Ø For nonionic, neutral molecules - Ø g ≈ 1 for m ≤ 0. 1 M or Ac = [C] For gases, - g ≈1 for pressures ≤ 1 atm or A ≈ P, where P is pressure in atm 8. ) Limitation of Debye-Hϋckel Equation Ø Ø Debye-Hϋckel predicts g decreases as m increases true up to m = 0. 10 M At higher m, the equation is no longer accurate at m ≥ 0. 5 M, most ions actually show an increase in g - with an increase in m at higher m, solvent is actually a mixture instead of just water Hydration sphere is mixture of water and salt at high concentration

Activity p. H 1. ) When we measure p. H with a p. H meter, we are measuring the negative logarithm of the hydrogen ion activity Ø Not measuring concentration 2. ) Affect of p. H with the Addition of a Salt Ø Changes ionic strength Changes H+ and OH- activity

Activity p. H 2. ) Affect of p. H with the Addition of a Salt Ø Example: What is the p. H of a solution containing 0. 010 M HCl plus 0. 040 M KCl. O 4?
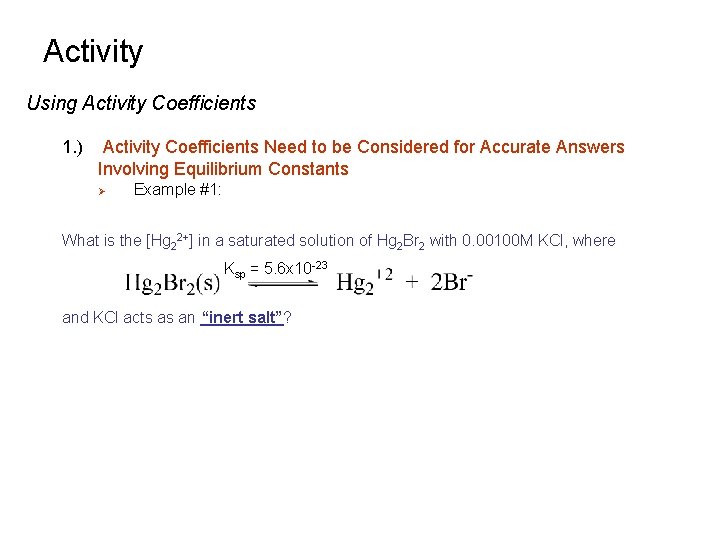
Activity Using Activity Coefficients 1. ) Activity Coefficients Need to be Considered for Accurate Answers Involving Equilibrium Constants Ø Example #1: What is the [Hg 22+] in a saturated solution of Hg 2 Br 2 with 0. 00100 M KCl, where Ksp = 5. 6 x 10 -23 and KCl acts as an “inert salt”?

Activity Using Activity Coefficients 1. ) Activity Coefficients Need to be Considered for Accurate Answers Involving Equilibrium Constants Ø Example #2: What is the [Hg 22+] in a saturated solution of Hg 2 Br 2 with 0. 00100 M KBr? Note: KBr is not an inert salt, since Br- is also present in the Ksp reaction of Hg 2 Br 2

Activity Using Activity Coefficients 1. ) Activity Coefficients Need to be Considered for Accurate Answers Involving Equilibrium Constants Ø Example #3: What is the true concentration of Li+ and F- in a saturated solution of Li. F in water? Note: Only Li. F is present in solution. Ionic strength is only determined by the amount of Li. F that dissolves Solution: Set-up the equilibrium equation in terms of activities Initial Concentration solid 0 0 Final Concentration solid x x
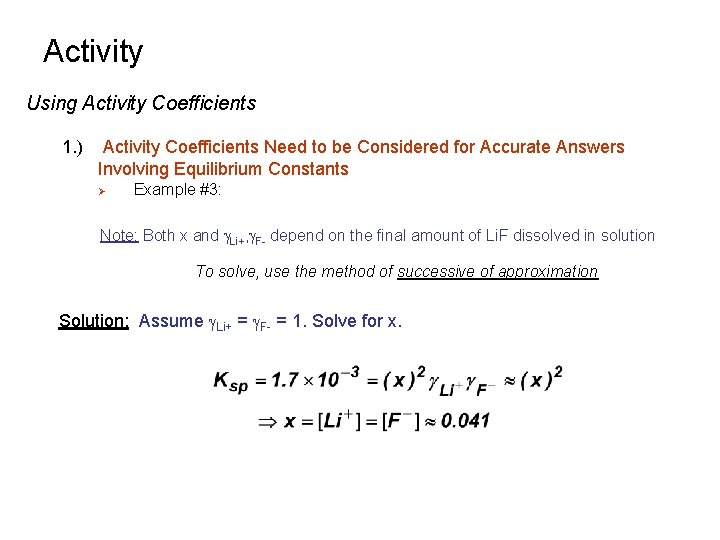
Activity Using Activity Coefficients 1. ) Activity Coefficients Need to be Considered for Accurate Answers Involving Equilibrium Constants Ø Example #3: Note: Both x and g. Li+, g. F- depend on the final amount of Li. F dissolved in solution To solve, use the method of successive of approximation Solution: Assume g. Li+ = g. F- = 1. Solve for x.

Activity Using Activity Coefficients 1. ) Activity Coefficients Need to be Considered for Accurate Answers Involving Equilibrium Constants Ø Example #3: Solution: Step 2 use the First Calculated Value of [Li+] and [F-] to Estimate the Ionic Strength and g Values. Obtained by using m=0. 041 and interpolating data in table

Activity Using Activity Coefficients 1. ) Activity Coefficients Need to be Considered for Accurate Answers Involving Equilibrium Constants Ø Example #3: Solution: Step 3 use the calculated values for g. F and g. Li to re-estimate [Li+] and [F-]. substitute

Activity Using Activity Coefficients 1. ) Activity Coefficients Need to be Considered for Accurate Answers Involving Equilibrium Constants Ø Example #3: Solution: Repeat Steps 2 -3 Until a Constant Value for x is obtained For this example, this occurs after 3 -4 cycles, where x = 0. 050 M Use concentrations to calculate new m and g. F, g. Li [F-], [Li+] Use g to calculate new concentrations.

Equilibrium Systematic Treatment of Equilibrium 1. ) Help Deal with Complex Chemical Equilibria Ø Ø Ø Set-up general equations Simplify using approximations Introduce specific conditions number of equations = number of unknowns 2. ) Charge Balance Ø The sum of the positive charges in solution equals the sum of the negative charges in solution. (positive charge) (negative charge) where [C] is the concentration of a cation n is the charge of the cation [A] is the concentration of an anion m is the charge of the anion A solution will not have a net charge!

Equilibrium Systematic Treatment of Equilibrium 2. ) Charge Balance Ø If a solution contains the following ionic species: H+, OH-, K+, H 2 PO 4 -, HPO 42 - and PO 43 -, the charge balance would be: The coefficient in front of each species always equals the magnitude of the charge on the ion. For a solution composed of 0. 0250 mol of KH 2 PO 4 and 0. 0300 mol of KOH in 1. 00 L: [H+] = 5. 1 x 10 -12 M [K+] = 0. 0550 M [OH-] = 0. 0020 M Charge balance: [H 2 PO 4 -] = 1. 3 x 10 -6 M [HPO 42 -] = 0. 0220 M [PO 43 -] = 0. 0030 M

Equilibrium Systematic Treatment of Equilibrium 3. ) Mass Balance Ø Ø Ø Also called material balance Statement of the conservation of matter The quantity of all species in a solution containing a particular atom must equal the amount of that atom delivered to the solution Acetic acid Acetate Mass balance for 0. 050 M in water: Include ALL products in mass balance: H 3 PO 4 H 2 PO 4 -, HPO 42 -, PO 43 -

Equilibrium Systematic Treatment of Equilibrium 3. ) Mass Balance Ø Example #1: Write the mass balance for a saturated solution of the slightly soluble salt Ag 3 PO 4, which produces PO 43 - and Ag+ when it dissolves. Solution: If phosphate remained as PO 43 -, then but, PO 43 - reacts with water

Equilibrium Systematic Treatment of Equilibrium 3. ) Mass Balance Ø Example #2: Write a mass balance for a solution of Fe 2(SO 4)3, if the species are Fe 3+, Fe(OH)2+, Fe 2(OH)24+, Fe. SO 4+, SO 42 - and HSO 4 -.

Equilibrium Systematic Treatment of Equilibrium 1. ) Write all pertinent reactions. 2. ) Write the charge balance equation. Ø Sum of positive charges equals the sum of negative charges in solution 3. ) Write the mass balance equations. There may be more than one. Ø Ø Conservation of matter Quantity of all species in a solution containing a particular atom must equal the amount of atom delivered to the solution 4. ) Write the equilibrium constant expression for each chemical reaction. Ø Only step where activity coefficients appear 5. ) Count the equations and unknowns Ø Number of unknowns must equal the number of equations 6. ) Solve for all unknowns 7. ) Verify any assumptions

Equilibrium Applying the Systematic Treatment of Equilibrium 1. ) Example #1: Ø Ionization of water Kw Kw = 1. 0 x 10 -14 at 25 o. C Step 1: Pertinent reactions: Step 2: Charge Balance: Step 3: Mass Balance Not True! : [H 2 O], [H+], [OH-] determined by Kw

Equilibrium Applying the Systematic Treatment of Equilibrium 1. ) Example #1: Ø Ionization of water Step 4: Equilibrium constant expression: Step 5: Count equations and unknowns: Two equations: (1) (2) Two unknowns: (1) (2)

Equilibrium Applying the Systematic Treatment of Equilibrium 1. ) Example #1: Ø Ionization of water Step 6: Solve: Ionic strength (m) of pure water is very low, g. H+ and g. OH- ~ 1 substitute

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 1: Pertinent reactions: This information is generally given: Ksp Kion pair Kacid Kbase Kw Ksp = 2. 4 x 10 -5 Kion pair = 5. 0 x 10 -3 Kacid = 2. 0 x 10 -13 Kbase = 9. 8 x 10 -13 Kw = 1. 0 x 10 -14

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 2: Charge Balance: Step 3: Mass Balance: Doesn’t matter what else happens to these ions!

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 4: Equilibrium constant expression (one for each reaction):

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Ø Ø Step 5: Count equations and unknowns: Seven Equations: (1) (CB) (2) (MB) (3) (4) (5) (6) (7) Seven Unknowns:

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 6: Solve (Not Easy!): - don’t know ionic strength don’t know activity coefficients - where to start with seven unknowns Make Some Initial Assumptions: Ø At first, set all activities to one to calculate ionic strength Ø At first, ignore equations with small equilibrium constants Ø [H+]=[OH-]=1 x 10 -7, remaining chemical reactions are independent of water

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 6: Solve (Not Easy!): Assumptions Reduce Number of Equations and Unknowns: Ø Three unknowns: Ø Three equations Mass balance and charge Charge balance: Mass balance: balance reduces to: [H+ ] =small [OH ]equilibrium Low concentrations -small equilibrium constant Low concentrations constant Simple Cancellation

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 6: Solve (Not Easy!): So, [Ca. SO 4] is known Therefore, only two equations and two unknowns: substitute and

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 6: Solve (Not Easy!): Given: Determine Ionic Strength: Determine Activity Coefficients: From table

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 6: Solve (Not Easy!): Use activity coefficients and Ksp equation to calculate new concentrations: Use new concentrations to calculate new ionic strength and activity coefficients:

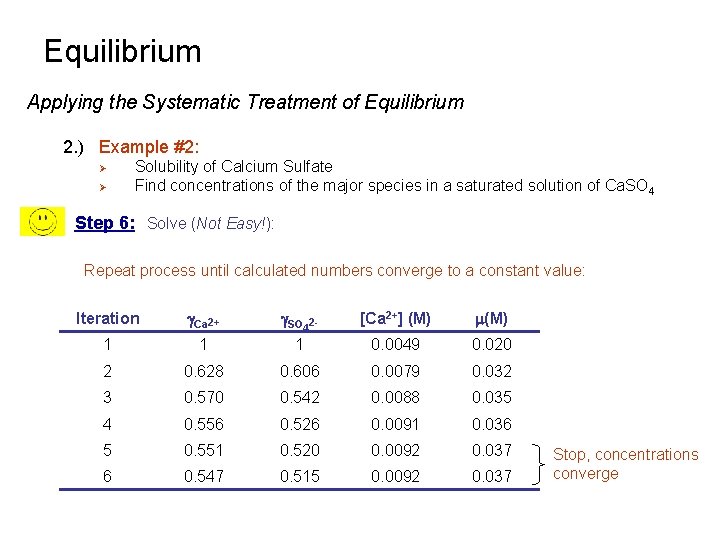
Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Ø Ø Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Step 6: Solve (Not Easy!): Repeat process until calculated numbers converge to a constant value: Iteration g. Ca 2+ g. SO 42 - [Ca 2+] (M) m(M) 1 1 1 0. 0049 0. 020 2 0. 628 0. 606 0. 0079 0. 032 3 0. 570 0. 542 0. 0088 0. 035 4 0. 556 0. 526 0. 0091 0. 036 5 0. 551 0. 520 0. 0092 0. 037 6 0. 547 0. 515 0. 0092 0. 037 Stop, concentrations converge

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #2: Solubility of Calcium Sulfate Find concentrations of the major species in a saturated solution of Ca. SO 4 Ø Ø Step 7: Check Assumptions: With: Both [HSO 4 -] and [Ca. OH+] are ~ 5 times less than [Ca 2+] and [SO 42 -] assumption is reasonable

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #3: Ø Ø Solubility of Magnesium Hydroxide Find concentrations of the major species in a saturated solution of Mg(OH)2 Step 1: Pertinent reactions: Ksp K 1 Kw Step 2: Charge Balance: Ksp = 7. 1 x 10 -12 K 1 = 3. 8 x 102 Kw = 1. 0 x 10 -14

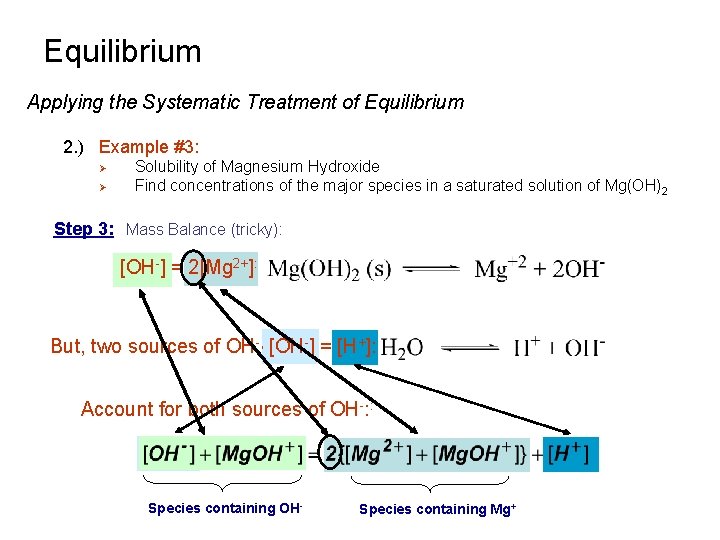
Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #3: Ø Ø Solubility of Magnesium Hydroxide Find concentrations of the major species in a saturated solution of Mg(OH)2 Step 3: Mass Balance (tricky): [OH-] = 2[Mg 2+]: But, two sources of OH-, [OH-] = [H+]: Account for both sources of OH-: : Species containing OH- Species containing Mg+

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #3: Ø Ø Solubility of Magnesium Hydroxide Find concentrations of the major species in a saturated solution of Mg(OH)2 Step 4: Equilibrium constant expression (one for each reaction): Proper to write equilibrium equations using activities, but complexity of manipulating activity coefficients is a nuisance. Most of the time we will omit activity coefficients

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #3: Ø Ø Solubility of Magnesium Hydroxide Find concentrations of the major species in a saturated solution of Mg(OH)2 Step 5: Count equations and unknowns: Four equations: (1) (2) (3) (4) Four unknowns: CB=MB

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #3: Ø Ø Solubility of Magnesium Hydroxide Find concentrations of the major species in a saturated solution of Mg(OH)2 Step 6: Solve (Not Easy!): Assumption to Reduce Number of Equations and Unknowns: Ø Solution is very basic [OH-] >> [H+], neglect [H+] CB=MB Rearrange K 1 (ignore activity coefficients):

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #3: Ø Ø Solubility of Magnesium Hydroxide Find concentrations of the major species in a saturated solution of Mg(OH)2 Step 6: Solve (Not Easy!): Substitute K 1 into Mass or Charge Balance: Solve for [Mg 2+]:

Equilibrium Applying the Systematic Treatment of Equilibrium 2. ) Example #3: Ø Ø Solubility of Magnesium Hydroxide Find concentrations of the major species in a saturated solution of Mg(OH)2 Step 6: Solve (Not Easy!): Substitute [Mg 2+] into Ksp equation: Reduces to a single equation with a single variable: Solve using spreadsheet, vary [OH-] until obtain correct value for Ksp (7. 1 x 10 -12)

Excel Demo of Goal Seek