Activity 6 Properties of Diagonals of Quadrilaterals Class

Objective To explore the similarities and differences between the different quadrilaterals like parallelogram, rectangle,

Materials Required • • • Glazed Papers Ruler A Pair of Scissors Pencil Tracing

Case II • Make a rectangle by paper folding on a glazed paper. Name

Place two replicas ∆BCA and ∆EFD such that AC and ED coincide each other

A Case III: • Make a rhombus by paper folding on a glazed paper.

Place two replicas ∆PQR and ∆MNO such that PR and MO coincide each other.

Draw and cut replicas of ∆AOB and ∆BOC and verify the congruency of two

Case IV: • Make a square by paper folding on a glazed paper. Name

Place two replicas ∆PQS and ∆PQR along their diagonals SQ and PR. Here, we

Draw and cut replicas of ∆POQ and ∆POS. Place these replicas one over another

Slides: 19

Download presentation

Activity- 6 Properties of Diagonals of Quadrilaterals Class 8 th Prepared & Presented By Mrs. Pramila Kumari Sahoo TGT, Mathematics JNV, Jagatsinghpur, Odisha

Objective To explore the similarities and differences between the different quadrilaterals like parallelogram, rectangle, rhombus and square with respect to their diagonals.

Pre-requisite Knowledge •

Materials Required • • • Glazed Papers Ruler A Pair of Scissors Pencil Tracing Paper

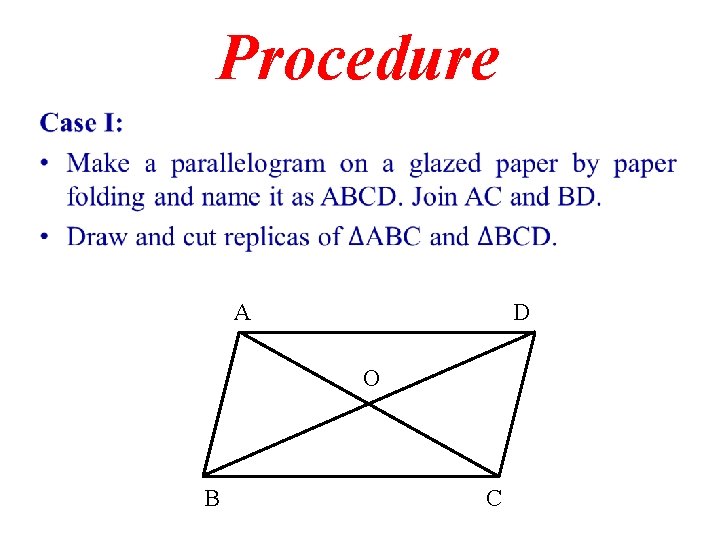
Procedure • A D O B C

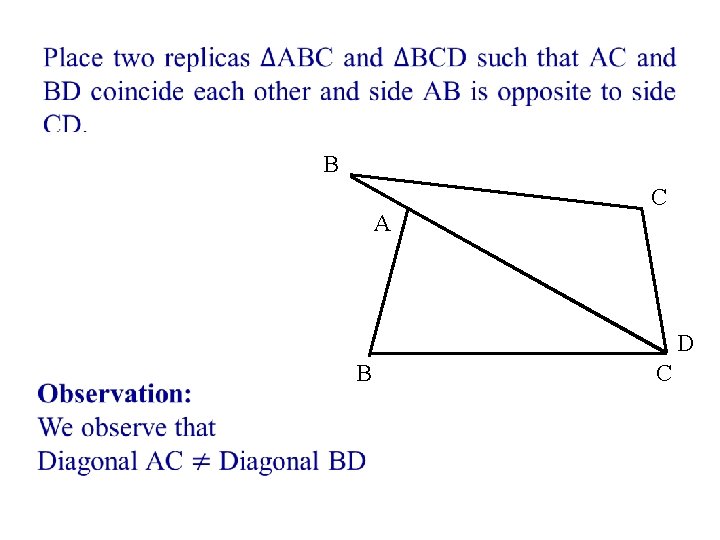
• B A C D B C

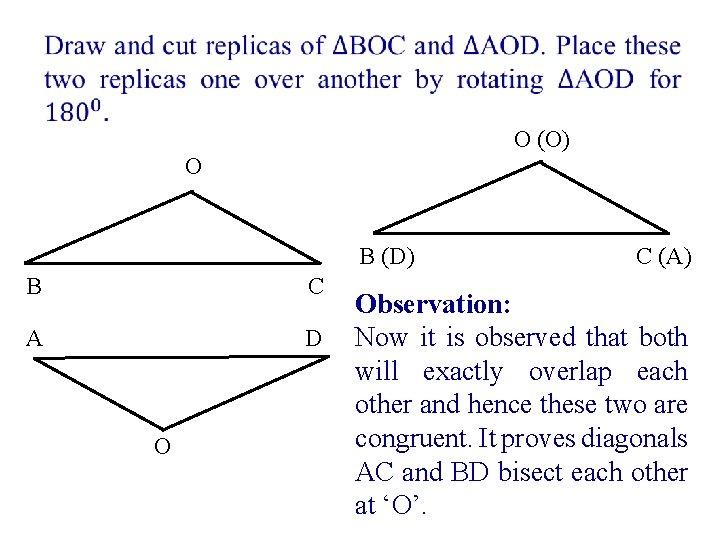
• O (O) O B (D) B C A D O C (A) Observation: Now it is observed that both will exactly overlap each other and hence these two are congruent. It proves diagonals AC and BD bisect each other at ‘O’.

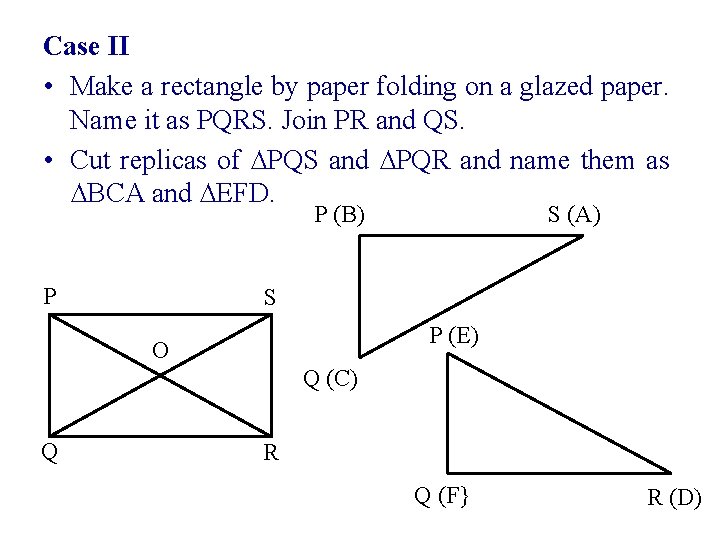
Case II • Make a rectangle by paper folding on a glazed paper. Name it as PQRS. Join PR and QS. • Cut replicas of ∆PQS and ∆PQR and name them as ∆BCA and ∆EFD. P (B) P S (A) S P (E) O Q (C) Q R Q (F} R (D)

Place two replicas ∆BCA and ∆EFD such that AC and ED coincide each other and side AB is opposite to side FD. A B E C Observation: D Here we notice that AC = DE. F (as they exactly overlap each other) ∴ diagonal AC = diagonal DE ∴ QS = PR Its diagonals also bisect each other at ‘O’ and can be proved as in the case of parallelogram

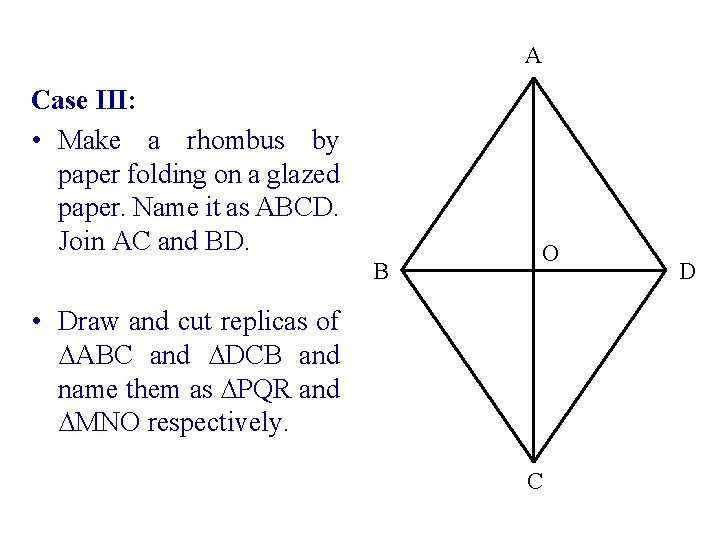
A Case III: • Make a rhombus by paper folding on a glazed paper. Name it as ABCD. Join AC and BD. B O • Draw and cut replicas of ∆ABC and ∆DCB and name them as ∆PQR and ∆MNO respectively. C D

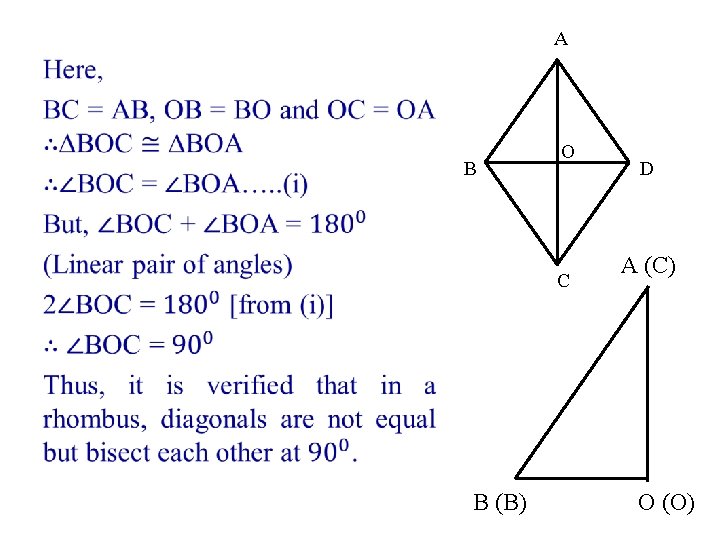
Place two replicas ∆PQR and ∆MNO such that PR and MO coincide each other. C (N) A (P) D (M) B (O) B (Q) Observation: It is observed that PR ≠ OM. ∴ diagonal AC ≠ diagonal BD C (R)

Draw and cut replicas of ∆AOB and ∆BOC and verify the congruency of two triangles by placing one over other. And it will be observed that they will exactly overlap with each other. B A B O O C A (C) B (B) O (O)

A • B O C B (B) D A (C) O (O)

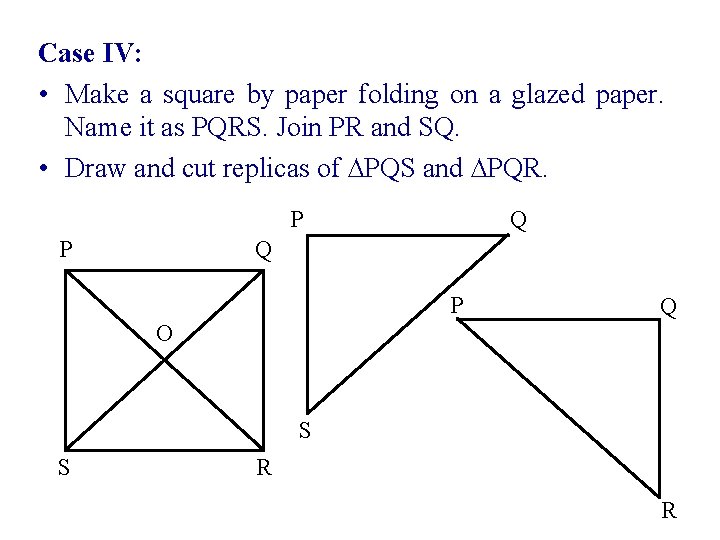
Case IV: • Make a square by paper folding on a glazed paper. Name it as PQRS. Join PR and SQ. • Draw and cut replicas of ∆PQS and ∆PQR. P P Q Q P O Q S S R R

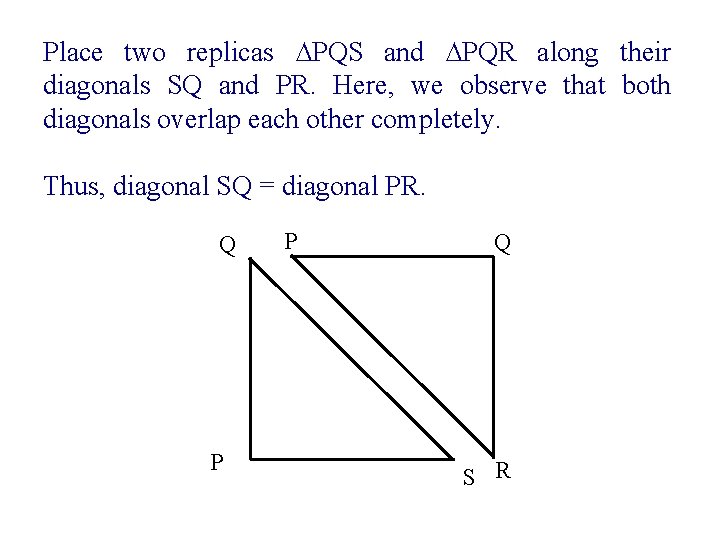
Place two replicas ∆PQS and ∆PQR along their diagonals SQ and PR. Here, we observe that both diagonals overlap each other completely. Thus, diagonal SQ = diagonal PR. Q P P Q S R

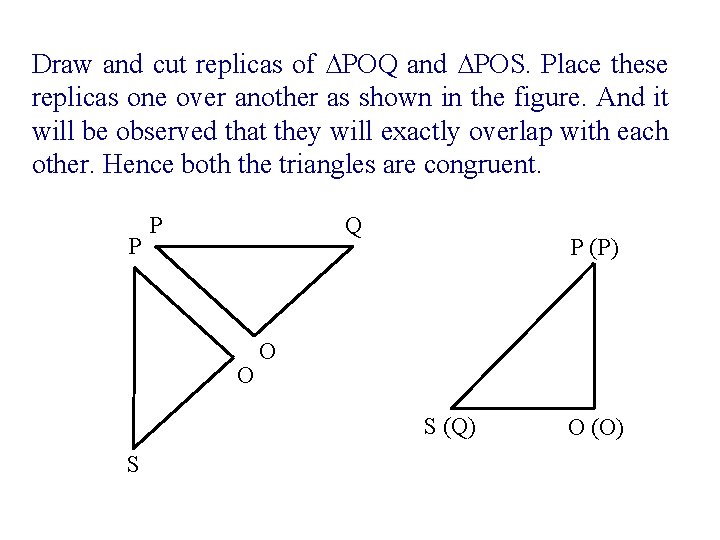
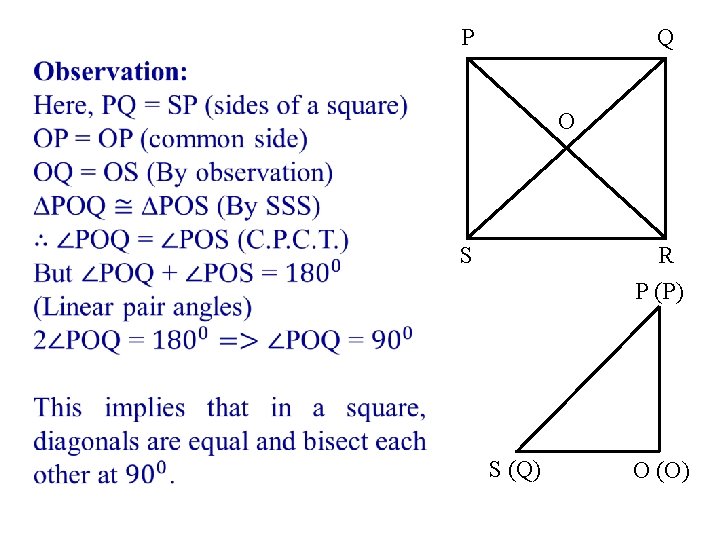
Draw and cut replicas of ∆POQ and ∆POS. Place these replicas one over another as shown in the figure. And it will be observed that they will exactly overlap with each other. Hence both the triangles are congruent. P P Q O P (P) O S (Q) S O (O)

P Q O S R P (P) S (Q) O (O)

Result •

Thank You