Activity 15 Quadrilateral A polygon with 4 sides

Activity 15

Quadrilateral • A polygon with 4 sides

Special Quadrilaterals • Parallelogram: quadrilateral with both sides parallel • Rhombus: a parallelogram with 4 congruent sides • Rectangle: a parallelogram with 4 right angles

• Square: a parallelogram with 4 congruent sides and 4 right angles • Kite: A quadrilateral with two pairs of adjacent sides congruent • Trapezoid: a quadrilateral with exactly one pair of parallel sides

15. 3: Properties of Parallelograms

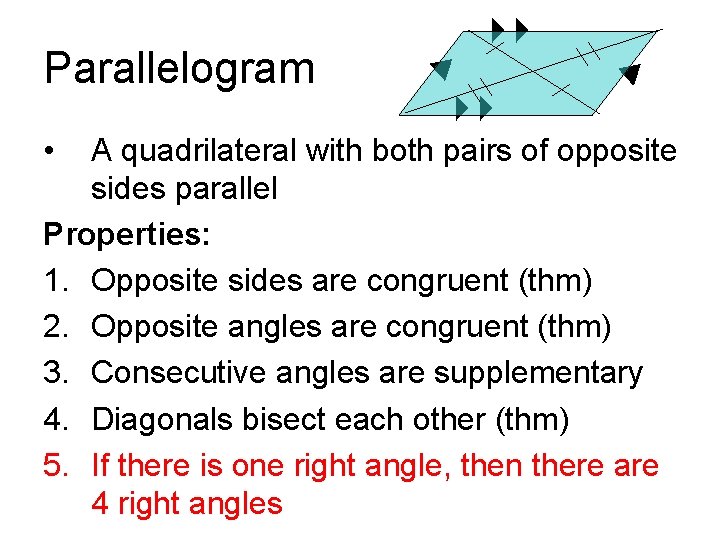
Parallelogram • A quadrilateral with both pairs of opposite sides parallel Properties: 1. Opposite sides are congruent (thm) 2. Opposite angles are congruent (thm) 3. Consecutive angles are supplementary 4. Diagonals bisect each other (thm) 5. If there is one right angle, then there are 4 right angles

Find the variables/measurements 1. b = ? 2. m RST = ? 3. m STU = ? 4. m STR = ?

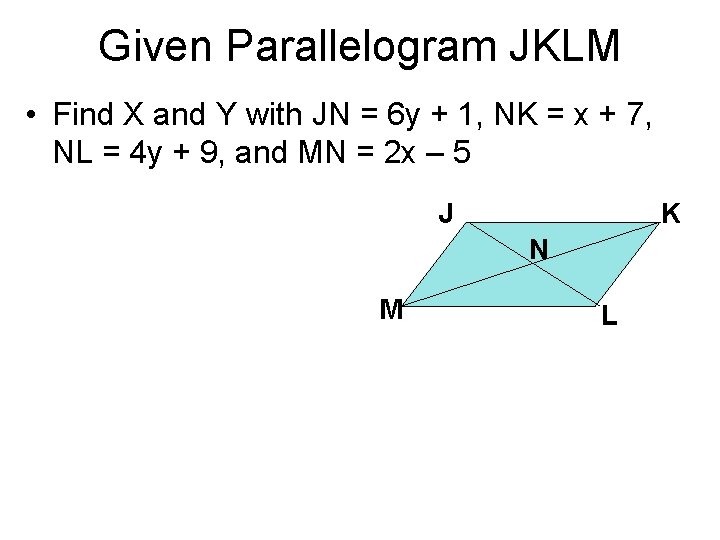
Given Parallelogram JKLM • Find X and Y with JN = 6 y + 1, NK = x + 7, NL = 4 y + 9, and MN = 2 x – 5 J K N M L

Theorem 6 -4 • If 3 or more parallel lines are cut off by congruent segments on one transversal, then they cut off congruent segments on every transversal. E A 8 B C 8 D 8 12. 5 Find EH. F 12. 5 G H

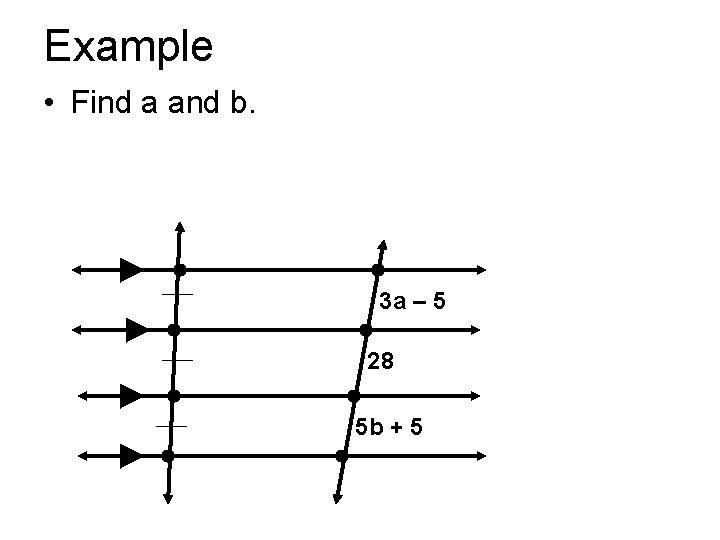
Example • Find a and b. 3 a – 5 28 5 b + 5

15. 4 Special Parallelograms

Rhombi • A parallelogram with all four sides congruent Rhombus Properties: • Diagonals of a rhombus are perpendicular • Each diagonal bisects a pair of opposite angles. Parallelogram Properties: • Opposite sides congruent and parallel • Opposite angles congruent • Diagonals bisect each other

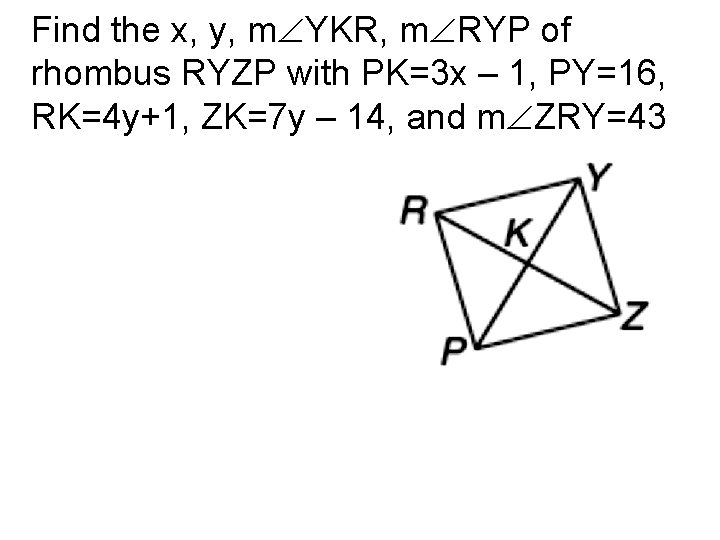
Find the x, y, m YKR, m RYP of rhombus RYZP with PK=3 x – 1, PY=16, RK=4 y+1, ZK=7 y – 14, and m ZRY=43

R S U T Rectangles • A parallelogram with four right angles Rectangle Properties: • Diagonals of a rectangle are congruent Parallelogram Properties: • Opposite sides congruent and parallel • Opposite angles congruent • Diagonals bisect each other

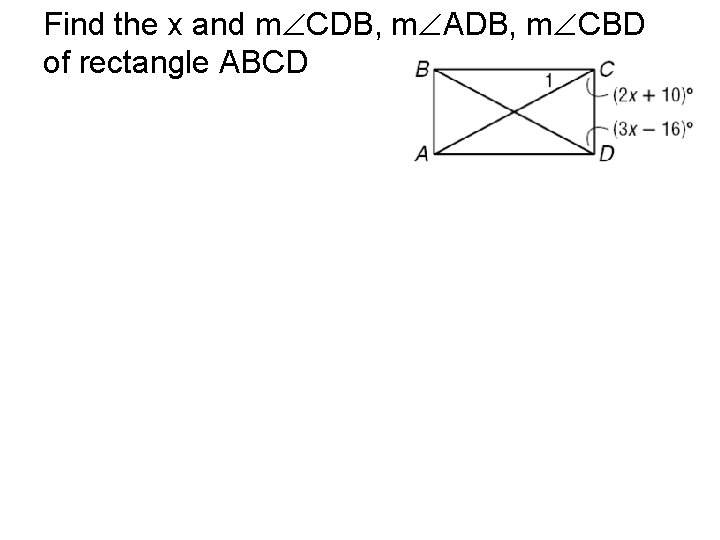
Find the x and m CDB, m ADB, m CBD of rectangle ABCD

Square • A parallelogram with 4 congruent sides and 4 right angles • Has all properties of parallelograms, rectangles, and rhombi – Opposite sides congruent and parallel – Diagonals are congruent, perpendicular, bisect each other and bisect pairs of opposite angles

Trapezoids

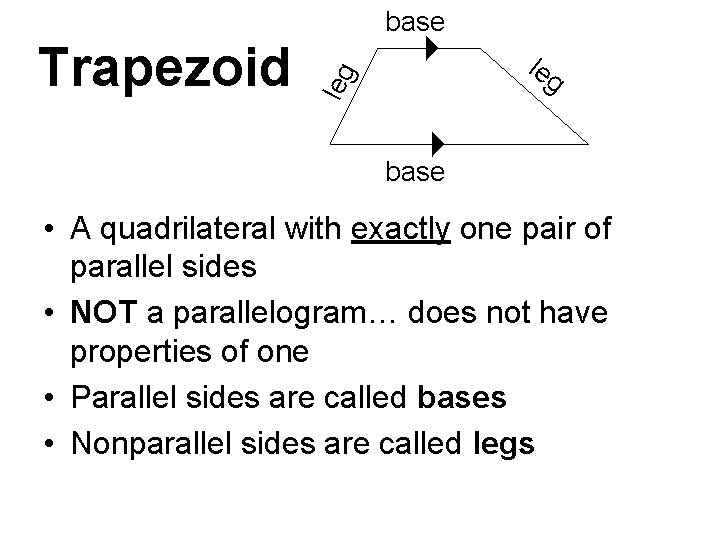
base leg Trapezoid leg base • A quadrilateral with exactly one pair of parallel sides • NOT a parallelogram… does not have properties of one • Parallel sides are called bases • Nonparallel sides are called legs

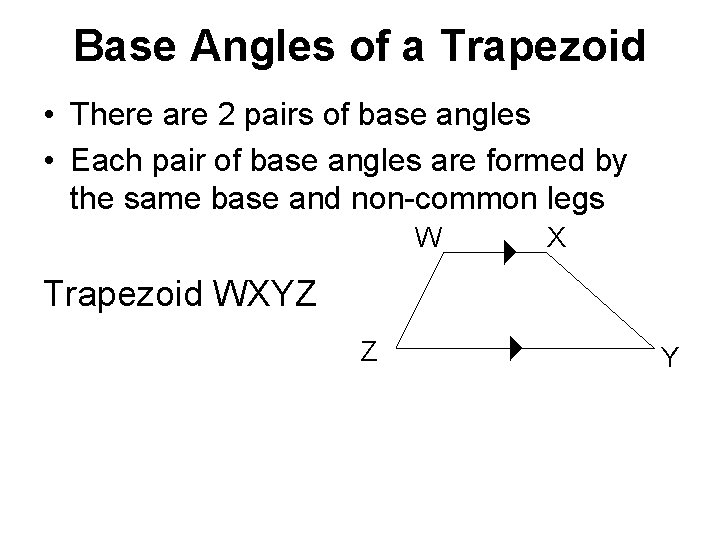
Base Angles of a Trapezoid • There are 2 pairs of base angles • Each pair of base angles are formed by the same base and non-common legs W X Trapezoid WXYZ Z Y

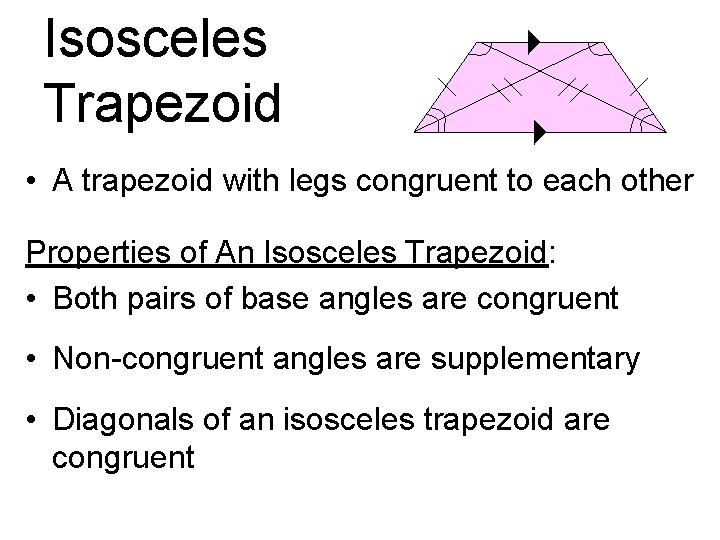
Isosceles Trapezoid • A trapezoid with legs congruent to each other Properties of An Isosceles Trapezoid: • Both pairs of base angles are congruent • Non-congruent angles are supplementary • Diagonals of an isosceles trapezoid are congruent

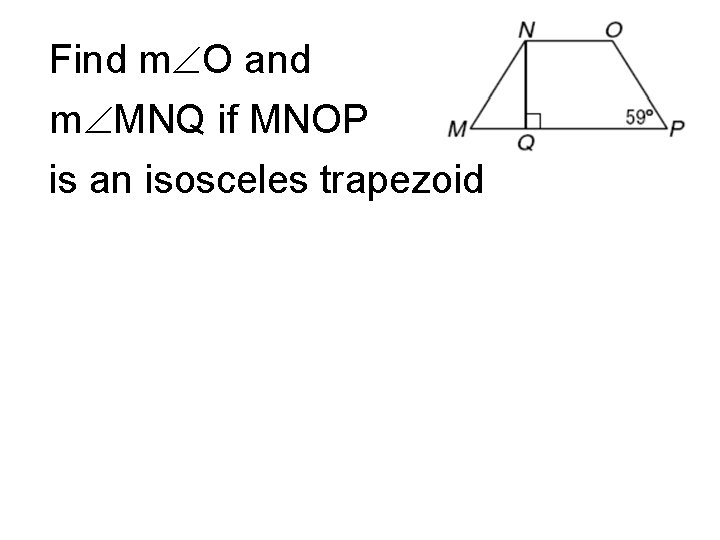
Find m O and m MNQ if MNOP is an isosceles trapezoid

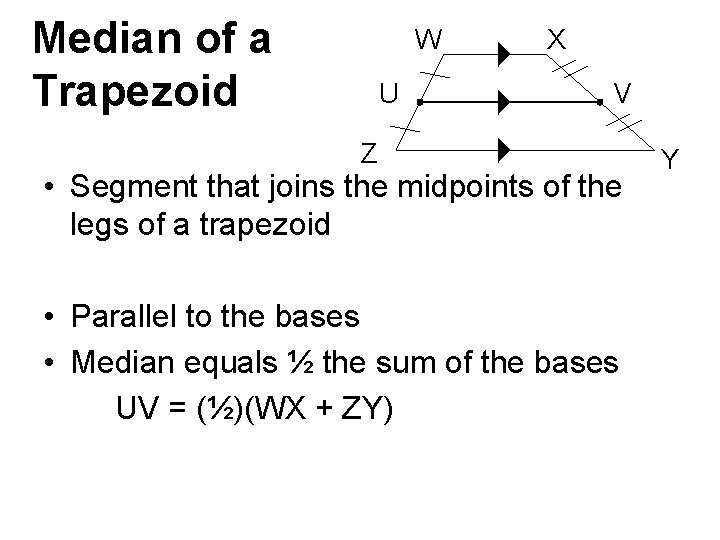
Median of a Trapezoid W U X V Z • Segment that joins the midpoints of the legs of a trapezoid • Parallel to the bases • Median equals ½ the sum of the bases UV = (½)(WX + ZY) Y

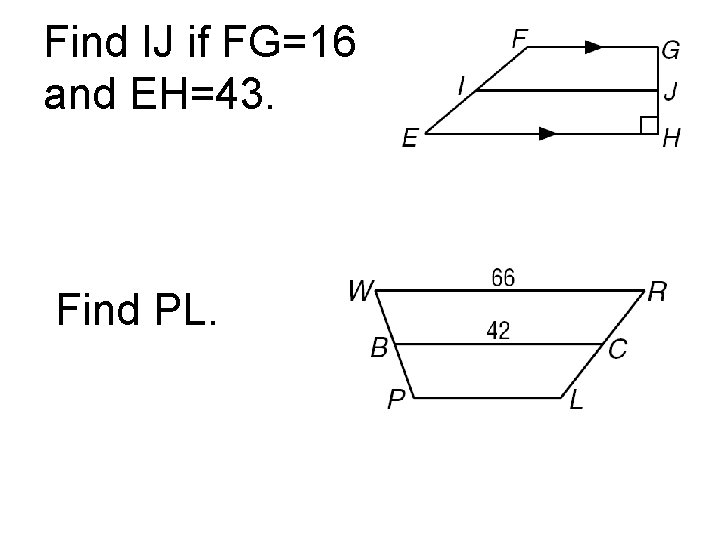
Find IJ if FG=16 and EH=43. Find PL.

Find the coordinates for the endpoints of the median of the trapezoid ABCD with A(1, 3), B(5, 0), C(8, -5), and D(-4, 4).

Other Quadrilaterals: Trapeziums and Kites

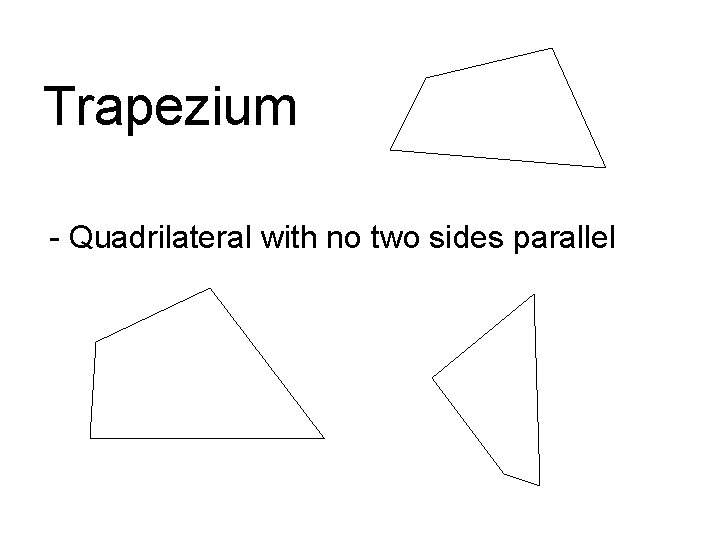
Trapezium - Quadrilateral with no two sides parallel

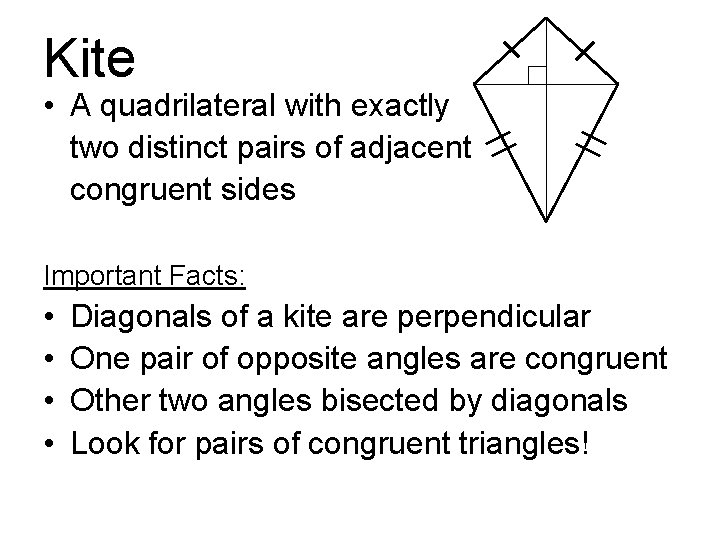
Kite • A quadrilateral with exactly two distinct pairs of adjacent congruent sides Important Facts: • • Diagonals of a kite are perpendicular One pair of opposite angles are congruent Other two angles bisected by diagonals Look for pairs of congruent triangles!

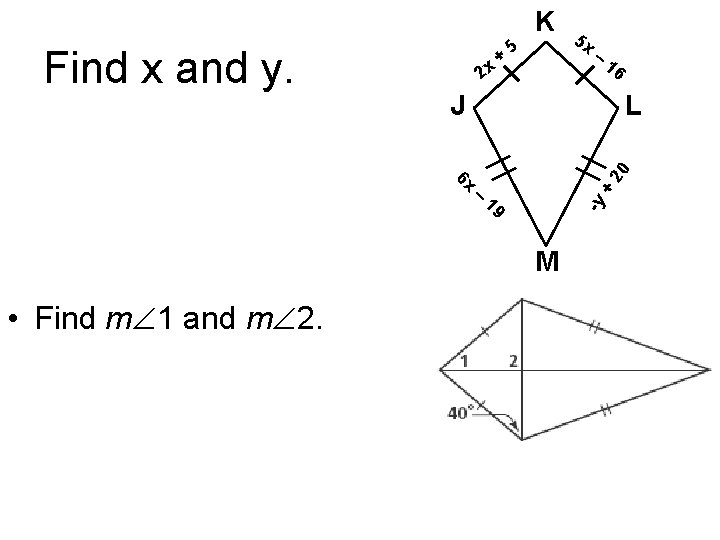
K 2 x – 16 L + – 20 J 6 x 19 M • Find m 1 and m 2. 5 x -y Find x and y. + 5