Activities for Proton Computed Tomography PCT Hartmut F

Activities for Proton Computed Tomography PCT Hartmut F. -W. Sadrozinski Santa Cruz Inst. for Particle Physics SCIPP State University of Loma Linda University New York at Medical Center Stony Brook UCSC Santa Cruz Institute of Particle Physics INFN Florence & Catania

The Proton CT Collaboration • • • http: //scipp. ucsc. edu/p. CT/ Proton Treatment: LLUMC Particle Tracking Systems: SCIPP, INFN Firenze Energy Detectors: BNL, LLUMC, INFN Catania Monte Carlo Simulation (GEANT 4): BNL, SCIPP, INFN, SLAC Image Reconstruction: SUNY Stony Brook • Goal –Develop proton CT for applications in proton therapy • Specific Aims –Design, construct and test components of a modular proton CT system –Develop, test, and optimize a dose-efficient image reconstruction algorithm –Evaluate performance of proton CT prototype

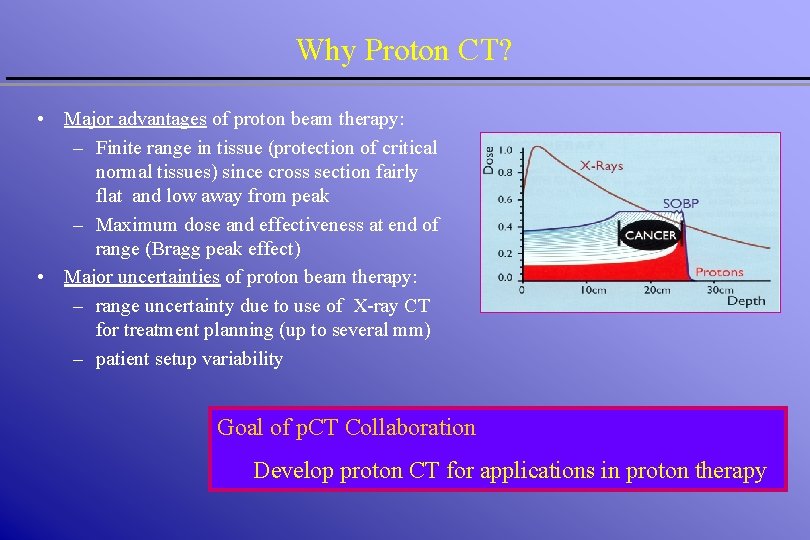
Why Proton CT? • Major advantages of proton beam therapy: – Finite range in tissue (protection of critical normal tissues) since cross section fairly flat and low away from peak – Maximum dose and effectiveness at end of range (Bragg peak effect) • Major uncertainties of proton beam therapy: – range uncertainty due to use of X-ray CT for treatment planning (up to several mm) – patient setup variability Goal of p. CT Collaboration Develop proton CT for applications in proton therapy

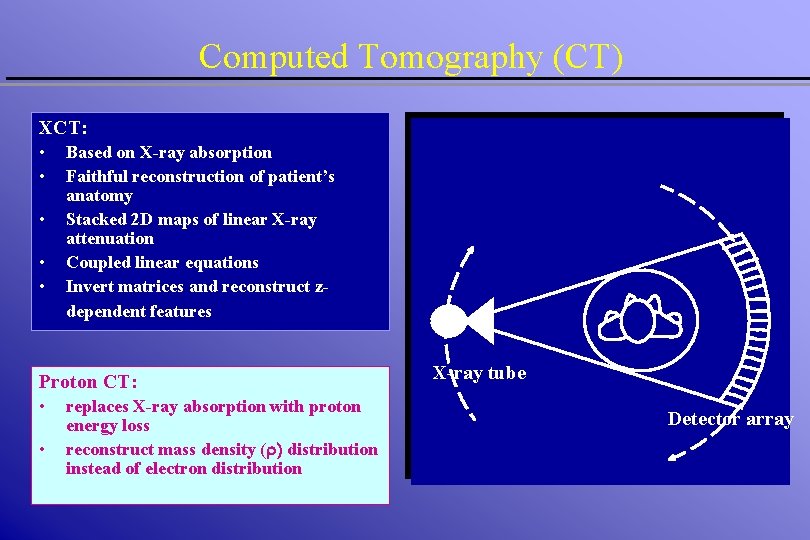
Computed Tomography (CT) XCT: • • • Based on X-ray absorption Faithful reconstruction of patient’s anatomy Stacked 2 D maps of linear X-ray attenuation Coupled linear equations Invert matrices and reconstruct zdependent features Proton CT: • • replaces X-ray absorption with proton energy loss reconstruct mass density (r) distribution instead of electron distribution X-ray tube Detector array

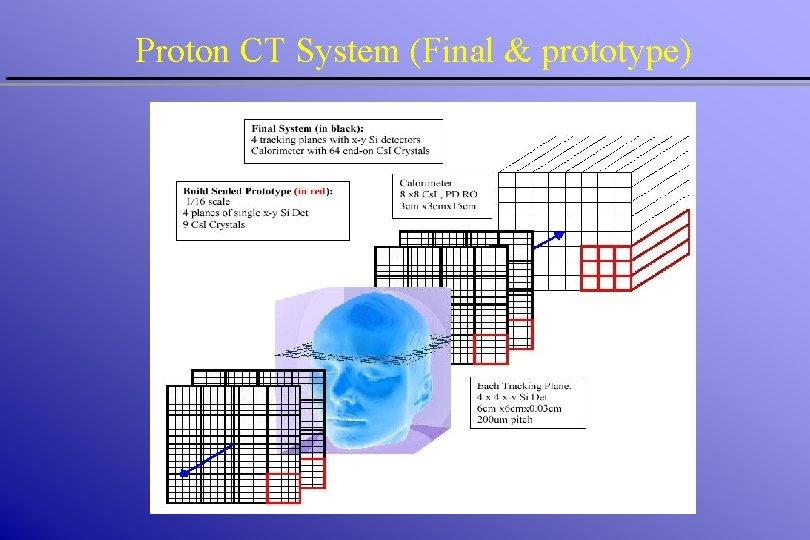
Proton CT System (Final & prototype)

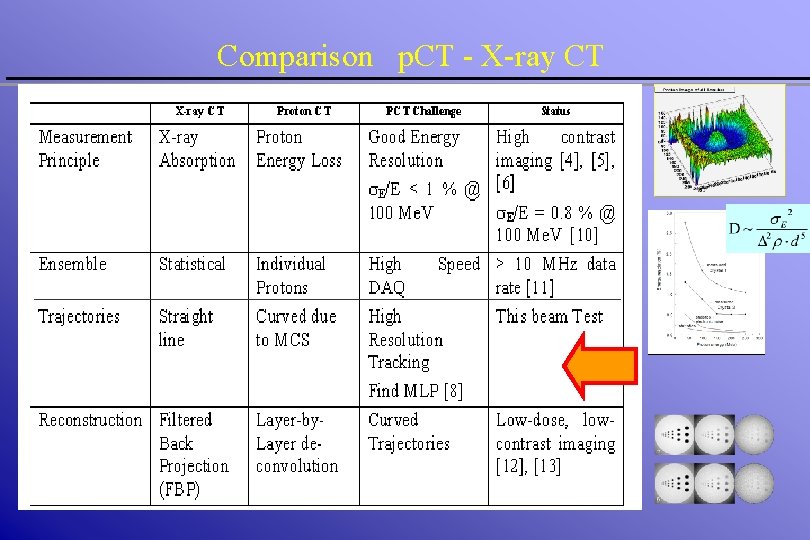
Comparison p. CT - X-ray CT

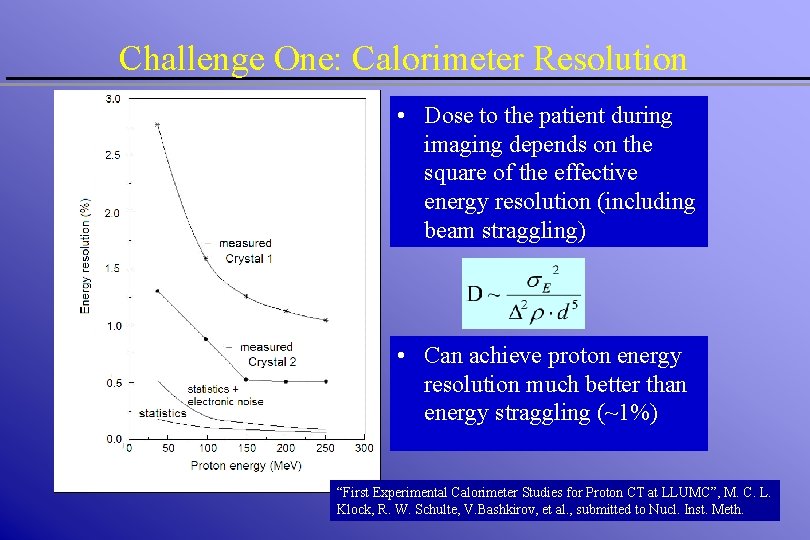
Challenge One: Calorimeter Resolution • Dose to the patient during imaging depends on the square of the effective energy resolution (including beam straggling) • Can achieve proton energy resolution much better than energy straggling (~1%) “First Experimental Calorimeter Studies for Proton CT at LLUMC”, M. C. L. Klock, R. W. Schulte, V. Bashkirov, et al. , submitted to Nucl. Inst. Meth.

Challenge Two: High-speed DAQ Hardware: Modular Commercial FPGA SSD PFME (NI 6534). Hartmut Sadrozinski et al. , IEEE TRANS ON NUCL. SCIE. , VOL. 51, NO. 5, 1

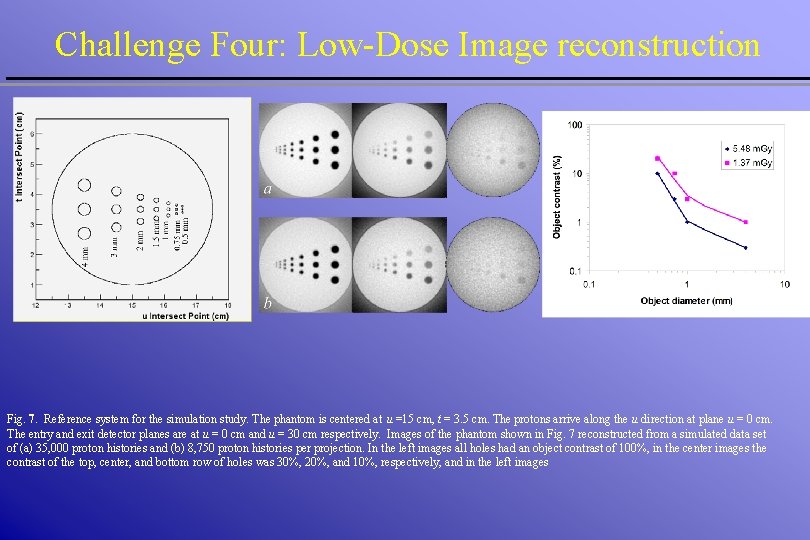
Challenge Four: Low-Dose Image reconstruction Fig. 7. Reference system for the simulation study. The phantom is centered at u =15 cm, t = 3. 5 cm. The protons arrive along the u direction at plane u = 0 cm. The entry and exit detector planes are at u = 0 cm and u = 30 cm respectively. Images of the phantom shown in Fig. 7 reconstructed from a simulated data set of (a) 35, 000 proton histories and (b) 8, 750 proton histories per projection. In the left images all holes had an object contrast of 100%, in the center images the contrast of the top, center, and bottom row of holes was 30%, 20%, and 10%, respectively, and in the left images

Challenge Four: Image of Al Annulus Subdivide SSD area into pixels 1. 2. Strip x strip 194 um x 194 um 4 x 4 strips (0. 8 mm x 0. 8 mm) Image corresponds to average energy in pixel “Initial studies on proton computed tomography using a silicon strip detector telescope”, L. Johnson et al. , NIM. A 514 (2003) 215

Beam Test Improvements • Improvements: – Increased precision of input parameters (entrance angle) needed to correct for beam divergence – Calorimeter DAQ – Geant 4 description of data and understanding of “Banana” in nonuniform medium • Next Steps: NON-uniform phantom (non-uniform density and/or shape, small aninal? ) • p. CT Reconstruction: FBP, Layer-by-layer deconvolution

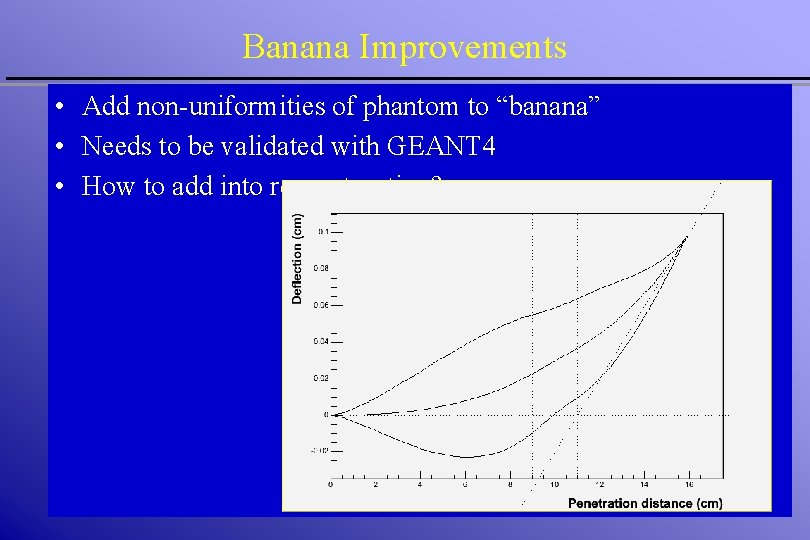
Banana Improvements • Add non-uniformities of phantom to “banana” • Needs to be validated with GEANT 4 • How to add into reconstruction?

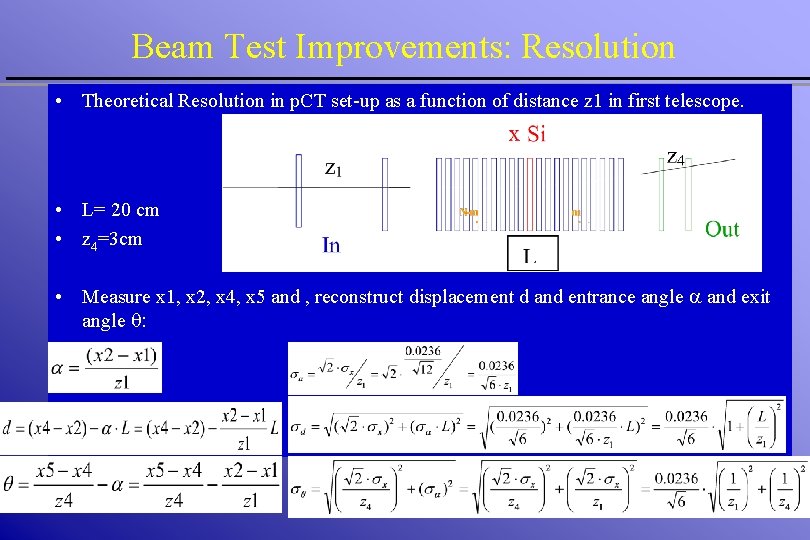
Beam Test Improvements: Resolution • Theoretical Resolution in p. CT set-up as a function of distance z 1 in first telescope. • In Tel • L= 20 cm • z 4=3 cm • Measure x 1, x 2, x 4, x 5 and , reconstruct displacement d and entrance angle a and exit angle q:

Beam Test Improvements: Resolution • Theoretical Resolution in p. CT set-up as a function of distance z 1 in first telescope. • Measure x 1, x 2, x 4, x 5 and , reconstruct displacement d and entrance angle a and exit angle q:

Acknowledgments LLUMC Reinhartd Schulte, MD Vladimir Bashkirov, Ph. D George Coutrakon, Ph. D Peter Koss, MS SUNY Stony Brook Jerome Z. Liang, Ph. D Klaus Mueller, Ph. D Tianfang Li (grad student) INFN Catania Pablo Cirrone, Ph. D Giacomo Cuttone, Ph. D Nunzio Randazzo, Ph. D Domenico Lo Presti, Engineer Valeria Sipali (grad student) Brookhaven National Laboratory Steve Peggs, Ph. D Todd Satogata, Ph. D Craig Woody, Ph. D Florence U. Mara Bruzzi, Ph. D David Menichelli, Ph. D Monica Scaringella (grad student) Santa Cruz Institute of Particle Physics Hartmut Sadrozinski, Ph. D Abe Seiden, Ph. D David C Williams, Ph. D Zhan Lang, Ph. D Brian Keeney (grad. Student) Jason Feldt (grad. Student) Jason Heimann (undergrad student) Dominic Lucia (undergrad student) Nate Blumenkrantz (undergrad student) Eric Scott (undergrad student)