Active Reinforcement Learning Ruti Glick BarIlan university 1

Active Reinforcement Learning Ruti Glick Bar-Ilan university 1

Active & Passive Learner Passive learner watches the world going by Has a fixed policy observes the state and reward sequences tries to learn utility of being in various states. After learning the utilities, actions can be chosen based on those utilities. 2

Active & Passive Learner Active learner consider what actions to take what their outcomes may be how they affect the rewards achieved act using learned information takes actions while it learns 3

The goal Decide which action to take each step Learn the environment Use learned knowledge to maximize received rewards 4

algorithms Adaptive Dynamic Programming (ADP) Temporal Difference (DT) Q – Learning sarsa 5

Adaptive dynamic programming for Active Learning 6

The Idea of ADP Choose an action at any step Learn the transition model of the environment Observe the effect s’ of performing a at state s Getting reward r at each visited state s Calculate utilities using bellman equations According to received transition model and rewards 7

Not like passive agents Agent has a choice of actions Doesn’t have fixed policy Choose best action to perform Has to learn complete model Outcome probabilities of all actions The utility it has to learn defined by optimal policy Solve using value iteration or policy iteration 8

Choosing Next Action Each step can find action that maximize utility If used value iteration – can calculate next step a = argmaxa(∑s’T(s, a, s’)U(s)) If used policy iteration – already has it Should it execute the action the optimal policy recommends? No! agent doesn’t learn the true utilities of optimal policy 9

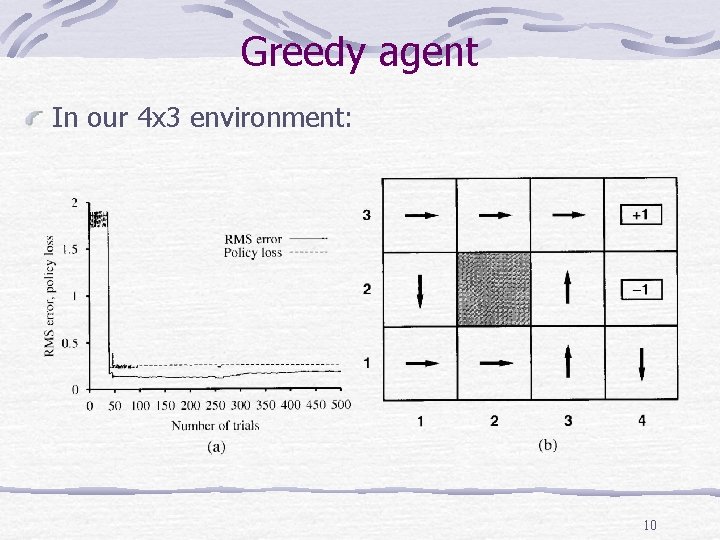
Greedy agent In our 4 x 3 environment: 10

Greedy agent (cont. ) Explanation: (a) RMS error in utility estimates (b) policy that the agent converged to In the 39 th trail agent get to +1 via (2, 1), (3, 2), (3, 3) From the 276 th trail it sticks to this policy 11

Greedy agent - summary conclusion Very seldom to converge to optimal policy for this environment Sometimes converge to awful policies Explanation Agent doesn’t learn the true model of true environment Can’t calculate optimal policy for true environment 12

Exploration & Exploitation: maximize agent’s reward Reflected by current utility estimation Exploration: maximize long-term well being. Try getting to unexplored states 13

Exploration Vs. Exploitation (Cont. ) Pure Exploitation risks getting stuck in a rut Pure exploration is useless The knowledge is not being used Agent must make trade-off between Continuing in a comfortable existence striking out into the unknown in the hopes of discovering a new and better life 14

approaches Two extreme approaches “greedy” approach: acts to maximize its utility using current model estimate acts randomly, in the hope that it will eventually explore the entire environment. Simple combine approach Choose random action a fraction 1/t of the time Follow the greedy policy otherwise 15

More sensible approach idea Give weight to actions the agent hasn't tried very often tending to avoid actions that believed to be of low utility change the constraint equation assigns a higher utility estimate to relatively unexplored action-state pairs. 16

More sensible approach (Cont. ) We will define U+(s) as optimistic estimation of U(s) U+(s) R(s) + maxa f( s’T(s, a, s’)U+(s’), N(a, s)) where N(a, s): number of times action a has been tried in state s. f(u, n): exploration function. Increasing in u (exploitation) Decreasing in n (exploration) 17

Exploration function Possible simple definition F(u, n) = { R+ u if n<Ne otherwise where R+(s) is optimistic estimate of best possible reward obtainable in any state Ne is a fixed parameter Makes agent try each action-state pair at least Ne times 18

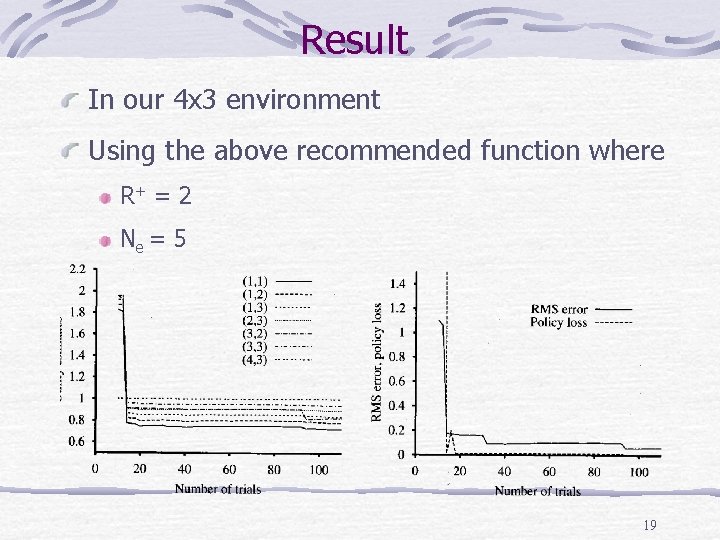
Result In our 4 x 3 environment Using the above recommended function where R+ = 2 Ne = 5 19

Temporal Difference Learning Agent for Active Learning 20

The Idea of TD Choose an action at any step Same as Active ADP agent A argmaxaf( s’T(s, a, s’)U(s’), N(a, s)) Learn the transition model of the environment Observe the effect s’ of performing a at state s Getting reward r at each visited state s Need it in order to choose an action Calculate utilities using TD update rule Same as passive TD agent U(s) + α(R(s) + γ U(s’) − U(s)) 21

TD properties Algorithm will converge to the same values of ADP But more slowly Disadvantage Has to learn the transition & reward model 22

TD Solution Define Action – Value Function Q(a, s) Use one of two approaches Q – Learn Sarsa 23

Action – Value Function Learn action-value representation Instead of learning utilities Define : Q(s, a) Value of doing action a in state s U(s) = maxa. Q(s, a) Constraint equation must hold at equilibrium when the Q-values are correct Q(s, a) = R(s) + γ∑s’T(s, a, s’)maxa’Q(s’, a’) 24

Q - Learning 25

Idea Of Q – Learning In each step Choose an action for current state Observe s’ – result state Update Q(a, s) Set the maximum possible value. According to current value of table Q 26

Action Choosing Like APD and TD – many approaches choosing next action Random action fraction decreases over time a argmaxa’f(Q(s’, a’), Nsa[a’, s’]) Nsa[a’, s’] is number of times action a has been tried. Has to learn this information a argmaxa’Q(s’, a’) Achieves highest Q value Will use this approach 27

Update Equation Calculate when action a execute in s, leading to s’ Q(s, a)+α(R(s)+γmaxa’Q(s’, a’)–Q(s, a)) Update according to maximum value can be received next step 28

The algorithm function Q-Learning-Agent( percept) returns an action inputs: percept, a percept indicating the current state s and reward signal r static: Q, a table of action values indexed by state and action s, a, r, the previous state, action, and reward, initially null s’, a’, the next state and action Initialize Q(s, a) arbitrarily Repeat (for each episode): Initialize s to start state Repeat (for each step of episode) Choose action “a” given s using policy derived from Q Take action a, observe reward r and next state s’ Q(s, a) + α[r + γmaxa’Q(s’, a’) − Q(s, a )] s s’ until s is terminal 29

Properties Do not have to learn the model Learn optimal policy In our 4 x 3 environment Much slower than the ADP agent 30

Sarsa 31

Idea Of Sarsa Choose an action for current state In each step Observe s’ – result state Choose an action for next state Update Q(s, a) Set value according to chosen next action 32

Action Choosing Like APD and TD – many approaches choosing next action Random action fraction decreases over time a argmaxa’f(Q(s’, a’), Nsa[a’, s’]) Nsa[a’, s’] is number of times action a has been tried. a argmaxa’Q(s’, a’) Achieves highest Q value Will use this approach 33

Update Equation Calculate when action a execute in s, leading to s’ where action a’ will be executed Q(s, a)+α(R(s)+γQ(s’, a’)–Q(s, a)) Update according to next chosen action 34

The algorithm function Sarsa-Agent( percept) returns an action inputs: percept, a percept indicating the current state s and reward signal r static: Q, a table of action values indexed by state and action s, a, r, the previous state, action, and reward, initially null s’, a’, the next state and action Initialize Q(s, a) arbitrarily Repeat (for each episode): Initialize s to start state Choose a given s using policy derived from Q Repeat (for each step of episode) Take action a, observe r, s’ Choose a’ given s’ using policy derived from Q Q(s, a) + α[r + γQ(s’, a’) − Q(s, a)] s s’, a a’ until s is terminal 35

SARSA vs Q-learning SARSA Repeat (for each episode): Initialize s to start state Choose a given s using policy derived from Q Repeat (for each step of episode) Take action a, observe r, s’ Choose a’ given s’ using policy derived from Q Q(s, a) + α[r + γQ(s’, a’) − Q(s, a)] s s’, a a’ until s is terminal Repeat (for each episode): Initialize s to start state Repeat (for each step of episode) Choose a given s using policy derived from Q Take action a, observe reward r and next state s’ Q(s, a) + α[r + γmaxa’Q(s’, a’) − Q(s, a )] s s’ until s is terminal 36

Properties Does not have to learn the model Find best policy Prove can’t be found yet in the literature The name “Sarsa” stands for: State, Action, Reward, State, Action the 5 elements of the update 37

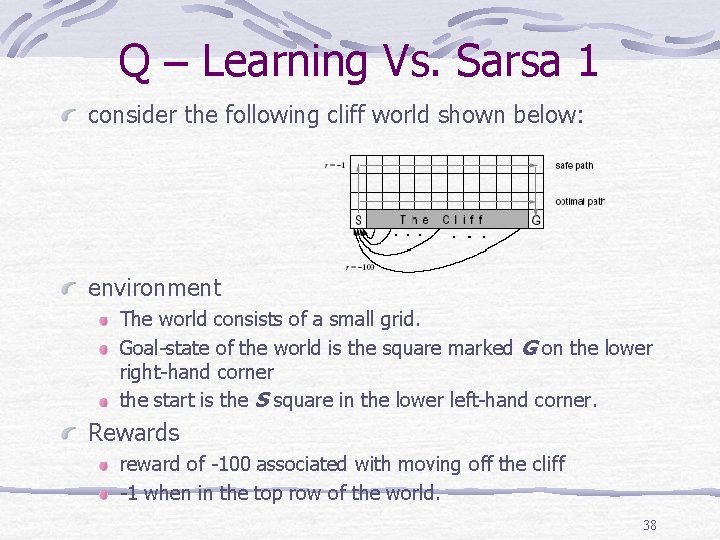
Q – Learning Vs. Sarsa 1 consider the following cliff world shown below: environment The world consists of a small grid. Goal-state of the world is the square marked G on the lower right-hand corner the start is the S square in the lower left-hand corner. Rewards reward of -100 associated with moving off the cliff -1 when in the top row of the world. 38

Q – Learning Vs. Sarsa (Cont. ) Cliff example Q-learning learns the optimal path along the edge of the cliff. falls off every now and then due to the e-greedy action selection. Sarsa learns the safe path, along the top row of the grid. takes the action selection method into account when learning. Sarsa actually receives a higher average reward per trial than Q - Learn learns the safe path does not walk the optimal path. 39

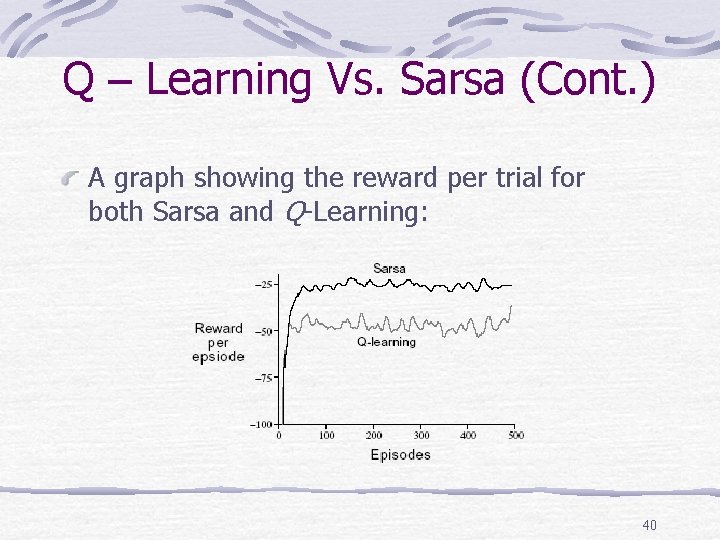
Q – Learning Vs. Sarsa (Cont. ) A graph showing the reward per trial for both Sarsa and Q-Learning: 40

On-Policy & Off-Policy Learning Off-Policy learning algorithms update the estimated value functions using hypothetical actions, those which have not actually been tried. For example: Q-learning updated Q(a, s) based upon an action we did not take maxa'Q(a', s') High cost of learning High learning quality 41

On-Policy & Off-Policy Learning (Cont. ) On-Policy learning methods which update value functions based strictly on experience. For example: Sarsa updated Q(a, s) based upon next chosen action Q(a’, s’) Choose safe actions while running 42