ACTIVE LEARNING ASSIGNMENTS DC CIRCUIT PREPARED BY 130400116023

ACTIVE LEARNING ASSIGNMENTS DC CIRCUIT PREPARED BY: 130400116023 - Patel Nidhi Harkishnbhai 130400116036 - Sharma Surabhi Chandra Deo BE First Semester IT Guided BY: Prof. P. R. Bhavsar DEPARTMENT OF ELECTRICAL ENGINEERING SANKALCHAND PATEL COLLEGE OF ENGINEERING, VISNAGAR

DC Circuits y. The circuit y. Resistance in combinations y. Kirchhoff’s Rules y. RC transient circuits

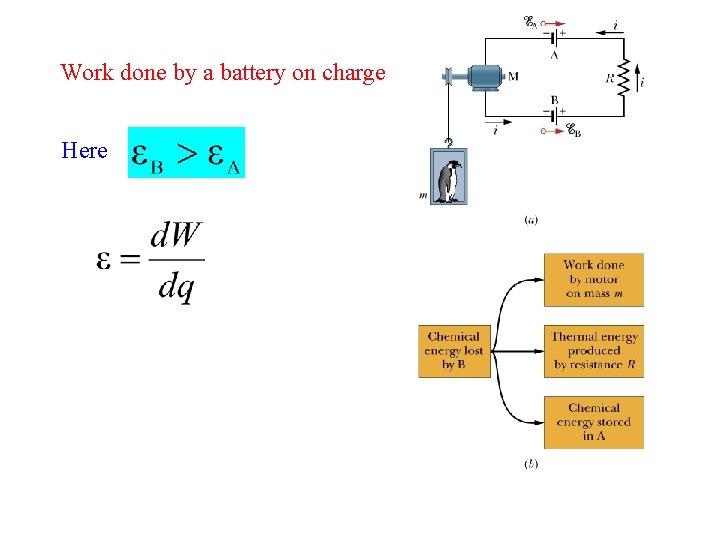
Work done by a battery on charge Here

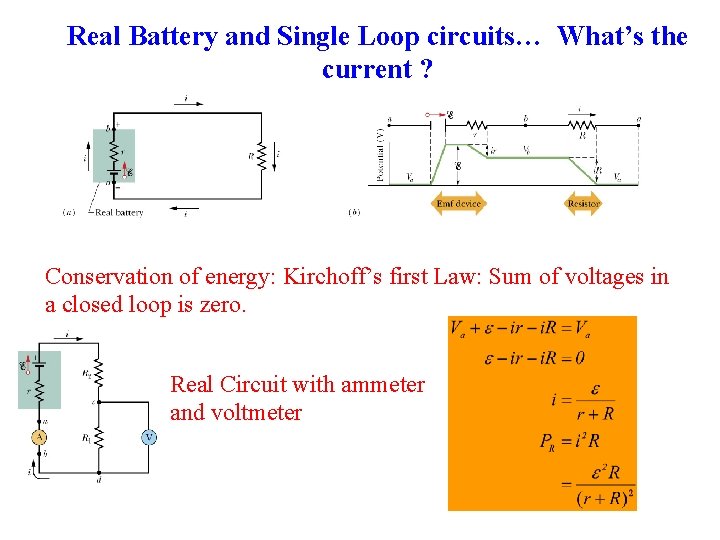
Real Battery and Single Loop circuits… What’s the current ? Conservation of energy: Kirchoff’s first Law: Sum of voltages in a closed loop is zero. Real Circuit with ammeter and voltmeter

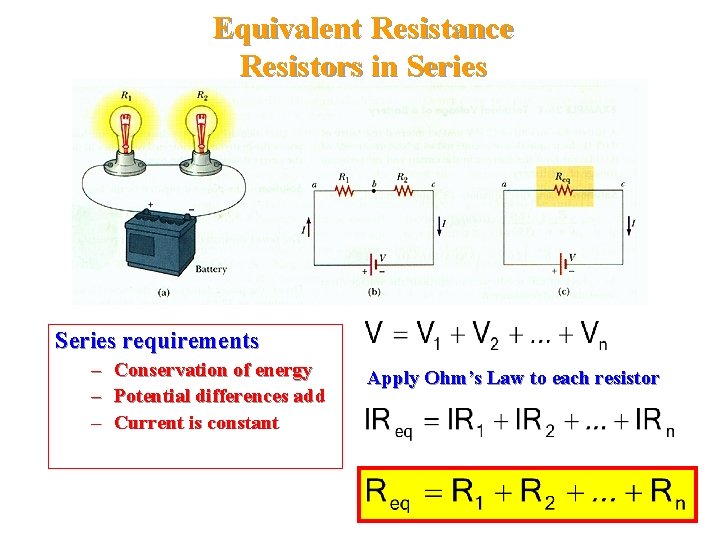
Equivalent Resistance Resistors in Series requirements – – – Conservation of energy Potential differences add Current is constant Apply Ohm’s Law to each resistor

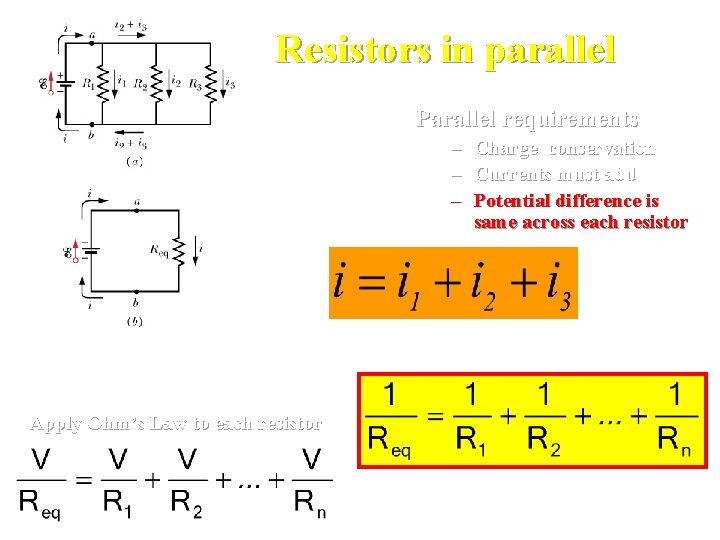
Resistors in parallel Parallel requirements – Charge conservation – Currents must add – Potential difference is same across each resistor Apply Ohm’s Law to each resistor

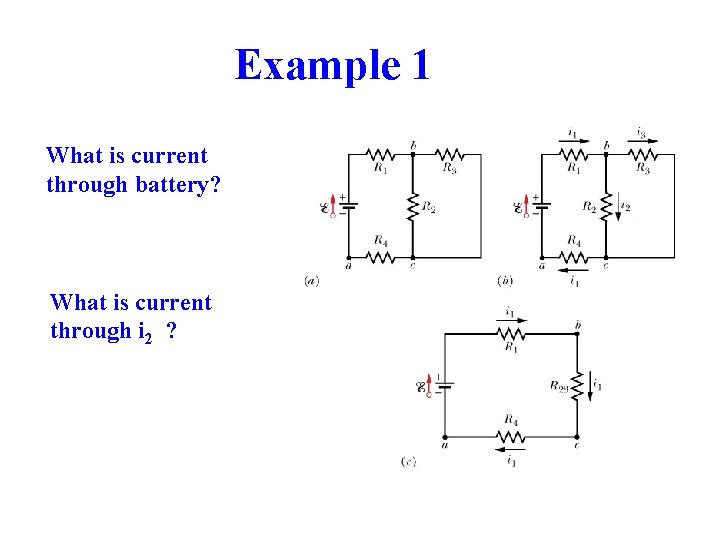
Example 1 What is current through battery? What is current through i 2 ?

Kirchhoff’s Rules 1 The algebraic sum of the currents entering a junction is zero. (Conservation of Charge) 2 The algebraic sum of the changes in electric potential difference around any closed circuit loop is zero. (Conservation of Energy) Signs for Rule 2 The direction of travel when traversing the loop is from a to b.

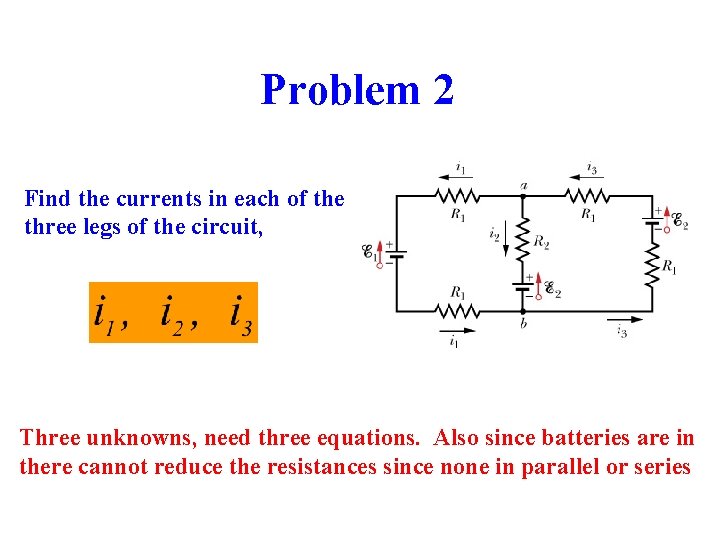
Problem 2 Find the currents in each of the three legs of the circuit, Three unknowns, need three equations. Also since batteries are in there cannot reduce the resistances since none in parallel or series

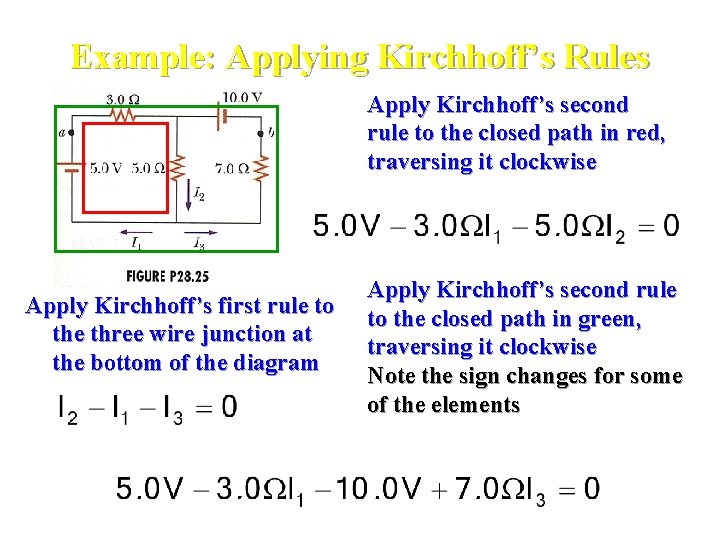
Example: Applying Kirchhoff’s Rules Apply Kirchhoff’s second rule to the closed path in red, traversing it clockwise Apply Kirchhoff’s first rule to the three wire junction at the bottom of the diagram Apply Kirchhoff’s second rule to the closed path in green, traversing it clockwise Note the sign changes for some of the elements

Another, example: applying Kirchhoff’s Rules Solve the equations simultaneously for the values if I. If I is negative the current is in the opposite direction

RC Circuits and Time dependence Resistor slows down the charging of the capacitor Time dependent behavior (transient) 2 cases: switch at “a” or at “b” a) Charging b) discharging

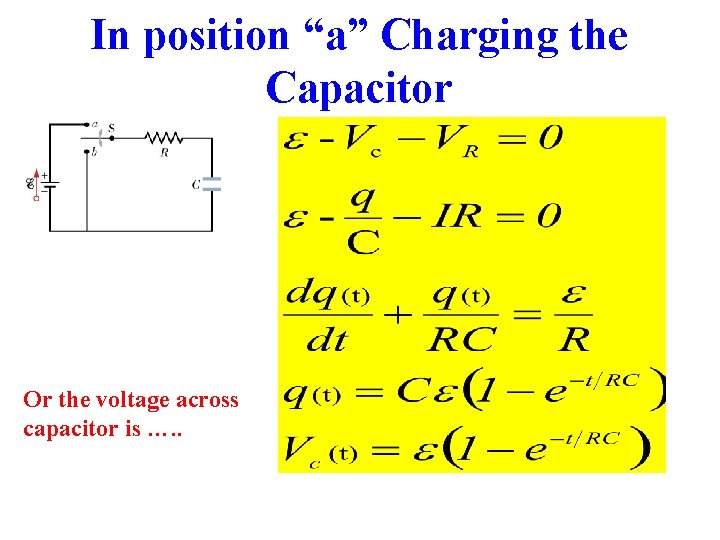
In position “a” Charging the Capacitor Use Kirchhoff’s Loop rule Or the voltage across capacitor is …. .

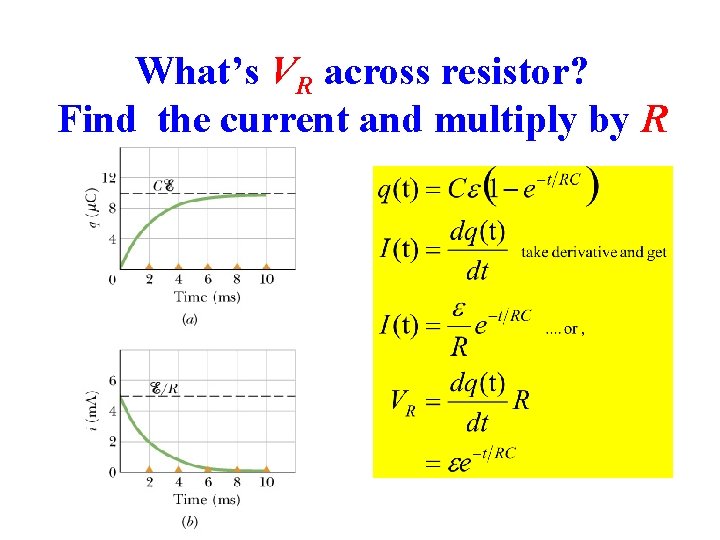
What’s VR across resistor? Find the current and multiply by R

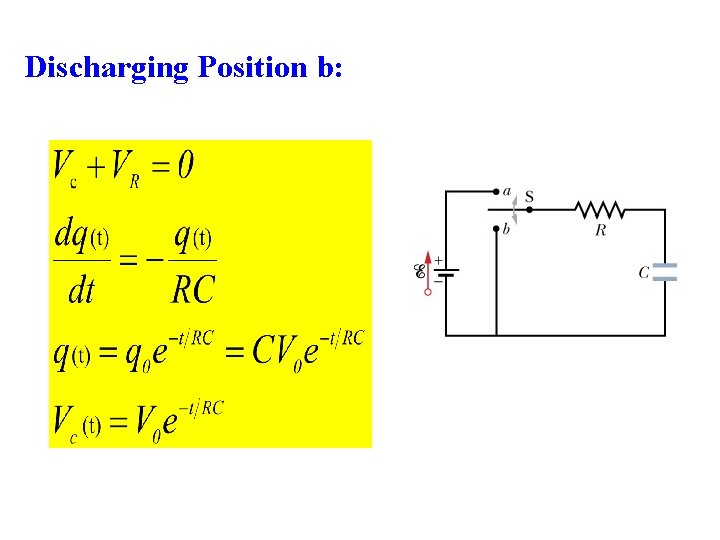
Discharging Position b:

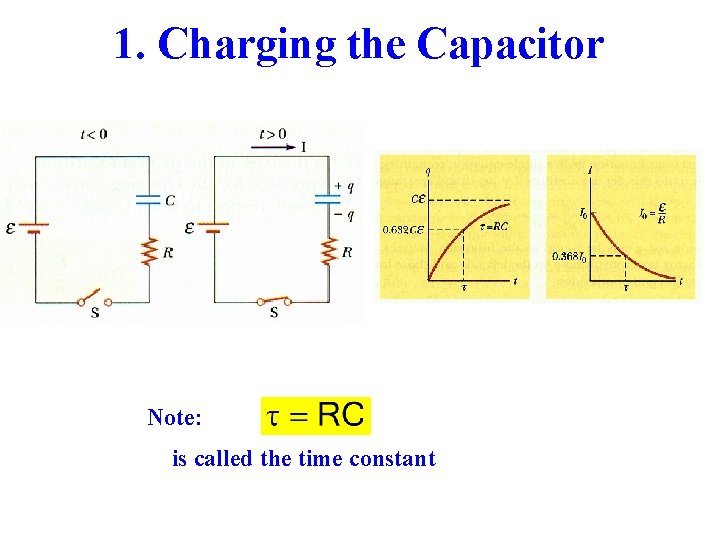
1. Charging the Capacitor Note: is called the time constant