Active Disturbance Rejection Control to Uncertain EulerBernoulli Beam

Active Disturbance Rejection Control to Uncertain Euler-Bernoulli Beam Equation Bao-Zhu Guo A new type of active disturbance rejection control Academy of Mathematics and Systems Science Academia Sinica July 1, 2018 BIT

1. ADRC: Active disturbance rejection control A control design method To copy with uncertainty in system Estimation + cancellation strategy Compare: Most of robust controls are in “worst case concern” July 1, 2018 BIT

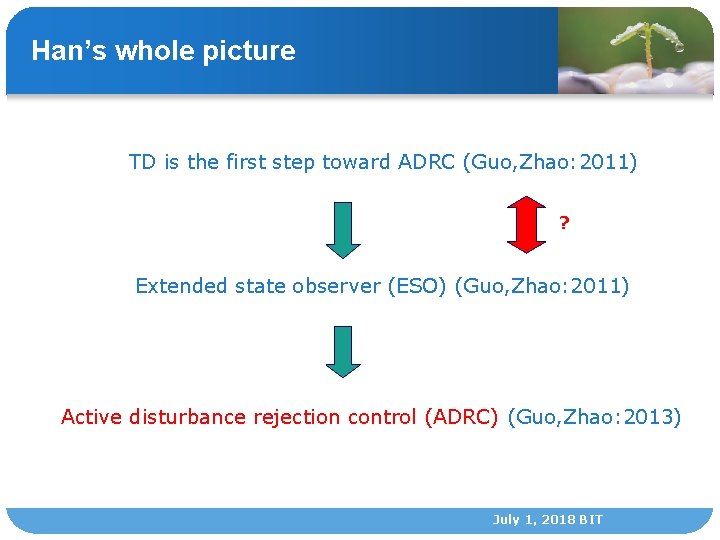
Han’s whole picture TD is the first step toward ADRC (Guo, Zhao: 2011) ? Extended state observer (ESO) (Guo, Zhao: 2011) Active disturbance rejection control (ADRC) (Guo, Zhao: 2013) July 1, 2018 BIT

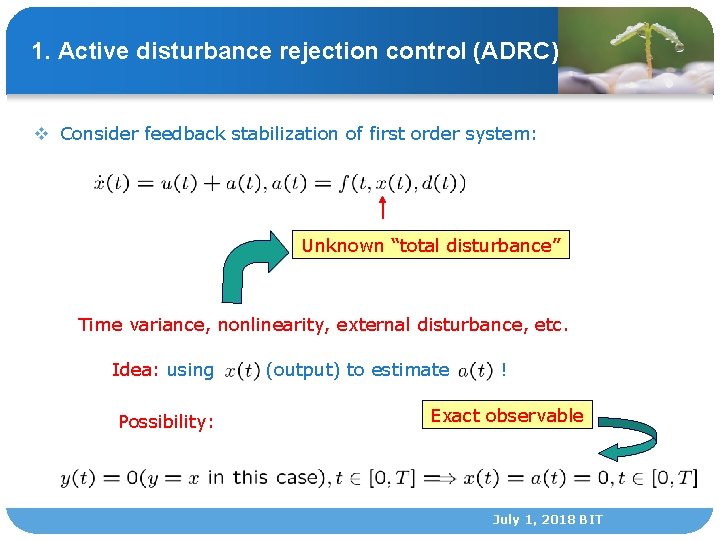
1. Active disturbance rejection control (ADRC) v Consider feedback stabilization of first order system: Unknown “total disturbance” Time variance, nonlinearity, external disturbance, etc. Idea: using Possibility: (output) to estimate ! Exact observable July 1, 2018 BIT

1. ADRC (cont’d) v Extended state observer (ESO): using output to estimate disturbance Injection output Let needs to be bounded Pole assignment for linear part: high gain choice July 1, 2018 BIT

Adaptive control: Example Consider Unknown parameter Expect: Control Parameter identification Closed-loop Lyapunov Parameter update law PE condition La. Sale principle: July 1, 2018 BIT

Why IMP works? Observable Output Let Exosystem: dynamics Not stabilizable System is observable! July 1, 2018 BIT

Why IMP works? Observer design Observer: Set Theorem Not necessary Control: July 1, 2018 BIT

J. V. Poncelet: measure disturbance July 1, 2018 BIT

G. Shipanov: invariance principle July 1, 2018 BIT

Han’s seminal idea (ESO): 1963 -66 Moscow Jingqing Han (1937 -2008) July 1, 2018 BIT

2. Observability: Infinite-dimensional system v For deterministic linear infinite-dimensional systems (i) (ii) (and hence for all ) Well-posed for output such that Observability inequality is continuous For uncertain systems, it should be coincident to this when uncertainty is zero July 1, 2018 BIT

2. Observability: uncertain system v for uncertain linear type infinite dimensional systems System is said to be observable if 1). When uncertainty is zero, system is exactly observable 2). The output can identify the uncertainty But what does it mean by this? Very recently, we gave an identification of uncertainty: uncertainty Of course you can use July 1, 2018 BIT

2. Observability: uncertain system (cont’d) Can we recover the state continuously from the output ? No This system is always observable So we cannot recover the state from the output continuously Note not in the same space In conclusion: uncertainty can only be “recognized’’ by output ! July 1, 2018 BIT

3. Problem: uncertain beam equation v Uncertain beam equation (i). Total disturbance Exponentially stable (ii). Under some condition We didn’t do this For observer, we do not need which is for feedback! July 1, 2018 BIT

3. Uncertain beam equation: observability v v Conservative Exponentially stable One is not enough System is exact observable with July 1, 2018 BIT

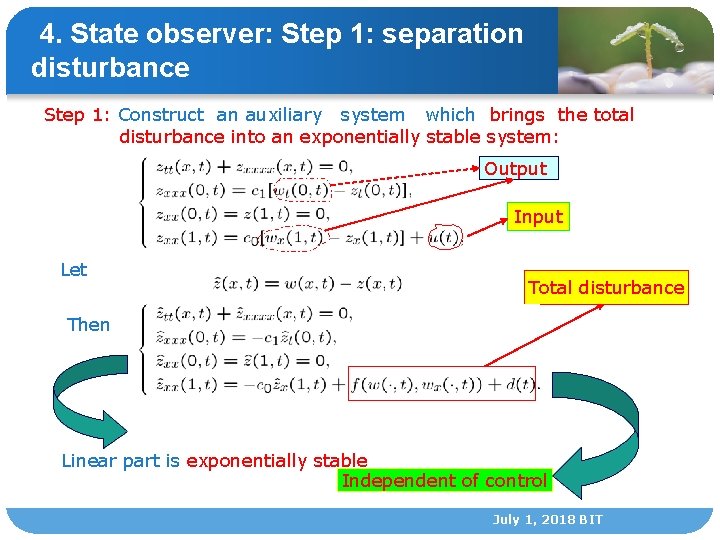
4. State observer: Step 1: separation disturbance Step 1: Construct an auxiliary system which brings the total disturbance into an exponentially stable system: Output Input Let Total disturbance Then Linear part is exponentially stable Independent of control July 1, 2018 BIT

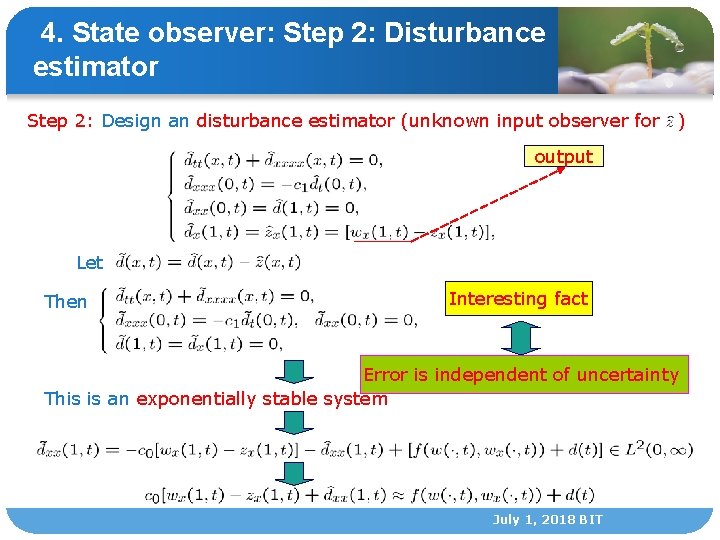
4. State observer: Step 2: Disturbance estimator Step 2: Design an disturbance estimator (unknown input observer for ) output Let Then Interesting fact Error is independent of uncertainty This is an exponentially stable system July 1, 2018 BIT

4: One unknown input observer v Putting together, we obtain a first unknown input observer output where It is not very convenient for control design July 1, 2018 BIT

4. State observer: Step 3: observer Step 3: Compensate the total disturbance by its estimate to obtain estimator based observer The observer is designed as Original Output Uncertainty compensation July 1, 2018 BIT

4: State observer: Unknown input observer Another unknown input observer: putting everything together Output No Input is used No high gain, No derivative of disturbance is required July 1, 2018 BIT

5. Observer based feedback: disturbance free Note: State feedback for observer is output feedback for original Observer: Observer is linear Cancel the disturbance by feedback is used here July 1, 2018 BIT

5. Closed-loop system: Total disturbance Output stabilizing feedback Closed-loop is still nonlinear! July 1, 2018 BIT

5. Nonlinear problem: linear method Make an invertible transformation: appeared previously Then the closed-loop is equivalent to Linear part and nonlinear part in next page July 1, 2018 BIT

5. Nonlinear problem: linear method (cont’d) Nonlinear part: Interesting fact II Nonlinear inhomogeneous But determined by linear The “cascade” structure avoids the nonlinear difficulty! Nonlinear problem can be treated by linear method July 1, 2018 BIT

5. Convergence of closed-loop Theorem: Subsystems bounded Convergence Internal stable July 1, 2018 BIT

6. Conclusions ● Active disturbance rejection control to PDE with internal uncertainty and external disturbance ● Estimation/cancelation strategy ● No high gain is used (perhaps infinite gain due to PDE? ) ● No derivative boundedness of disturbance is assumed ● Applicable to multi-dimensional PDEs July 1, 2018 BIT

New book on ADRC July 1, 2018 BIT

---The end--- July 1, 2018 BIT