ACTIVE CONTROL OF A GAS FLOW RATE IN

ACTIVE CONTROL OF A GAS FLOW RATE IN AN ALTERNATING GRADIENT DIFFUSION CHAMBER USING LABVIEW by Max Trueblood & David Le. Blanc ME 240 Semester Project MS&T, Rolla, MO 65401 7 MAY 2010 FN: 10507 507— 1200 ME 240 Project YES. pptx 1

OBJECTIVE: To actively control the outflow in the Alternating Gradient Diffusion Cloud Chamber (ALGR) based on the pressure drop across the sample metering tube inlet, so as to achieve stable operation, and thus improve data collection. 2

Figure 1. Green lines take dilution air to probe, while red lines take sample to instrumented trailer. Two one ton ingots of Pb hold probe securely. 3 3

Figure 2. Easing up into the contrail of the target plane to sample its particulates. 4

Figure 3. Sampling from a drone’s gas turbine engine at an engine rebuilding facility. Goal here was to try to burn up all C particles in extremely hot afterburner at right. 5

Dr Phil Whitefield Figure 4. Dr Whitefield inspects engine at a hush house in Amsterdam. 6

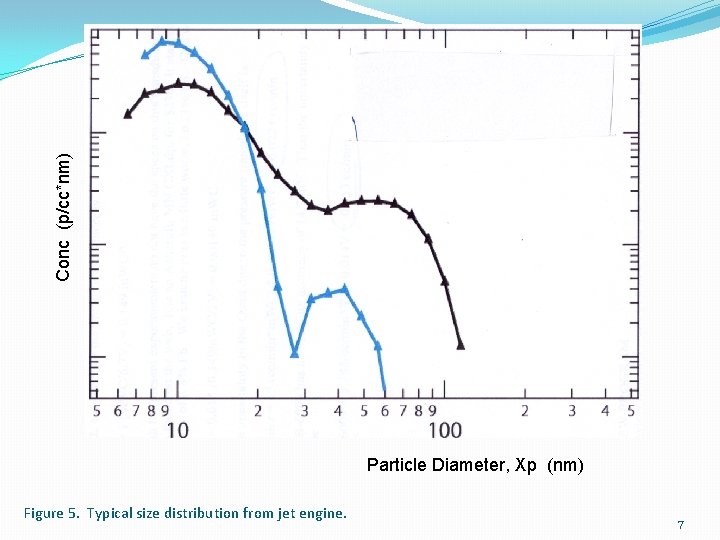
Conc (p/cc*nm) Particle Diameter, Xp (nm) Figure 5. Typical size distribution from jet engine. 7

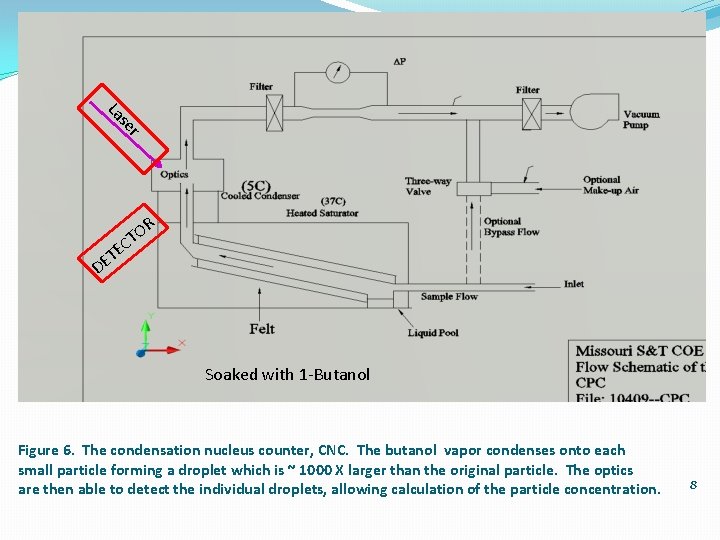
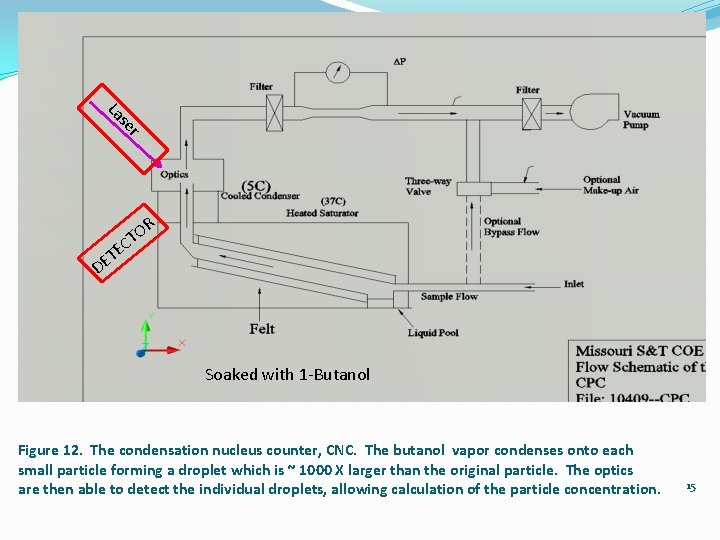
r se La R O T C E ET D Soaked with 1 -Butanol Figure 6. The condensation nucleus counter, CNC. The butanol vapor condenses onto each small particle forming a droplet which is ~ 1000 X larger than the original particle. The optics are then able to detect the individual droplets, allowing calculation of the particle concentration. 8

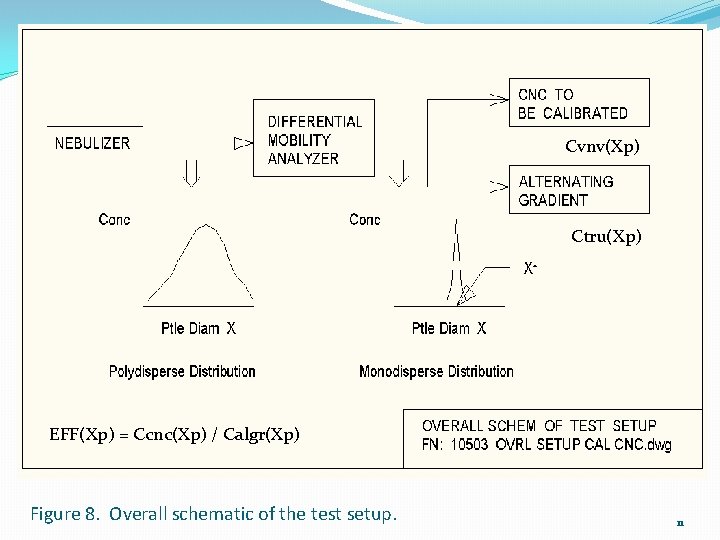
Since EFF(Xp) = Ccnc(Xp) / Ctru(Xp) The true concentration at diameter Xp is: Ctru(Xp) = [Ccnc(Xp) / EFF(Xp)] 9

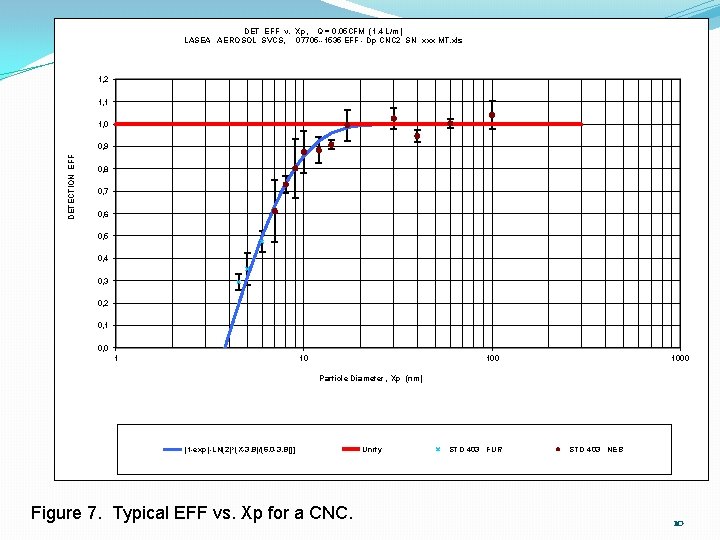
DET EFF v. Xp, Q = 0. 05 CFM (1. 4 L/m) LASEA AEROSOL SVCS, 07705 --1535 EFF - Dp CNC 2 SN xxx MT. xls 1, 2 1, 1 1, 0 DETECTION EFF 0, 9 0, 8 0, 7 0, 6 0, 5 0, 4 0, 3 0, 2 0, 1 0, 0 1 10 1000 Particle Diameter, Xp (nm) [1 -exp[-LN(2)*(X-3. 8)/(6. 0 -3. 8)]] Figure 7. Typical EFF vs. Xp for a CNC. Unity STD 403 FUR STD 403 NEB 10

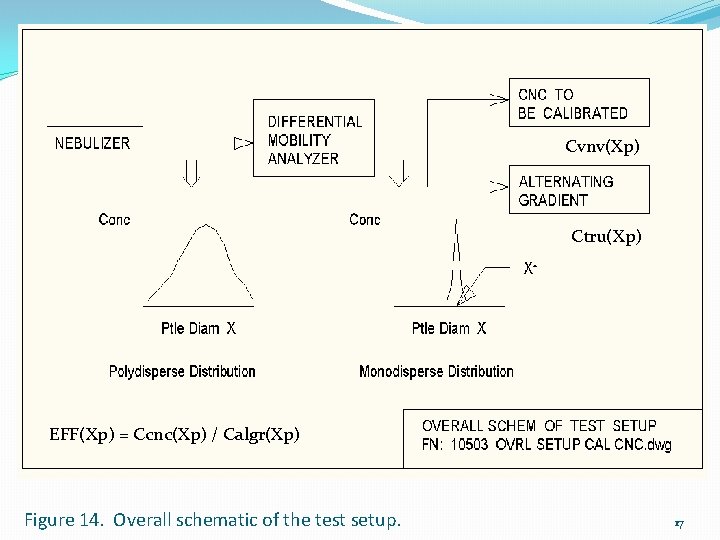
Cvnv(Xp) Ctru(Xp) EFF(Xp) = Ccnc(Xp) / Calgr(Xp) Figure 8. Overall schematic of the test setup. 11

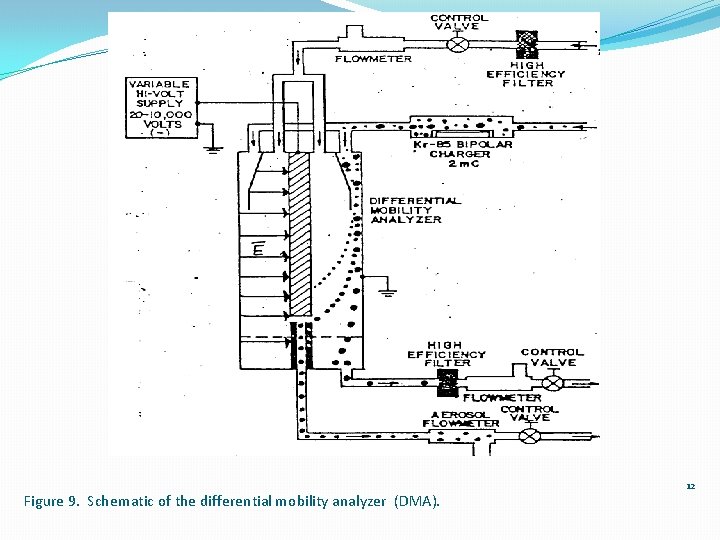
Figure 9. Schematic of the differential mobility analyzer (DMA). 12

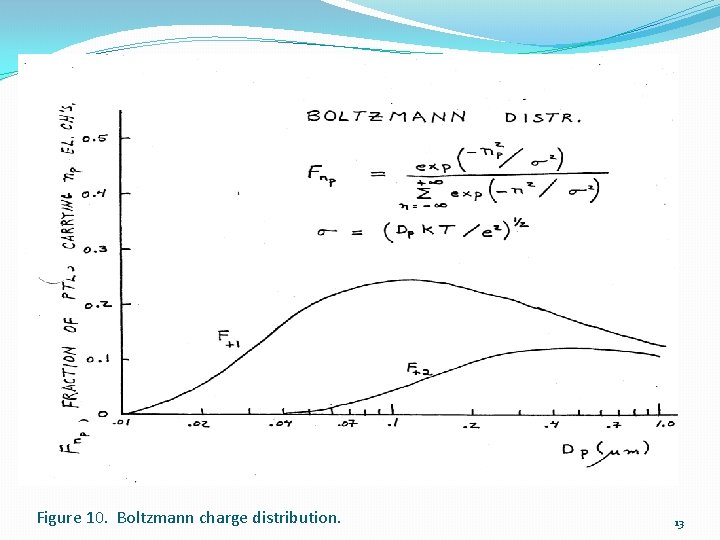
Figure 10. Boltzmann charge distribution. 13

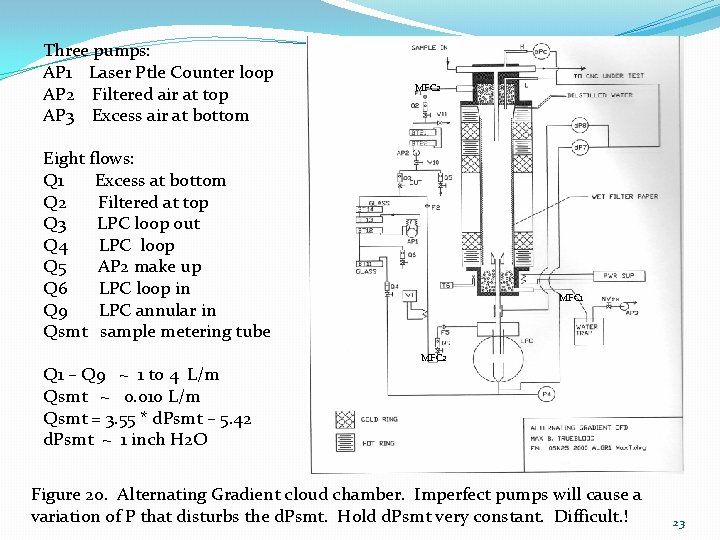
Three pumps: AP 1 Laser Ptle Counter loop AP 2 Filtered air at top AP 3 Excess air at bottom MFC 2 Eight flows: Q 1 Excess at bottom Q 2 Filtered at top Q 3 LPC loop out Q 4 LPC loop Q 5 AP 2 make up Q 6 LPC loop in Q 9 LPC annular in Qsmt sample metering tube Q 1 – Q 9 ~ 1 to 4 L/m Qsmt ~ 0. 010 L/m Qsmt = 3. 55 * d. Psmt – 5. 42 d. Psmt ~ 1 inch H 2 O MFC 1 MFC 2 Figure 11. Alternating Gradient cloud chamber. Imperfect pumps will cause a variation of P that disturbs the d. Psmt. Hold d. Psmt very constant. Difficult! 14

r se La R O T C E ET D Soaked with 1 -Butanol Figure 12. The condensation nucleus counter, CNC. The butanol vapor condenses onto each small particle forming a droplet which is ~ 1000 X larger than the original particle. The optics are then able to detect the individual droplets, allowing calculation of the particle concentration. 15

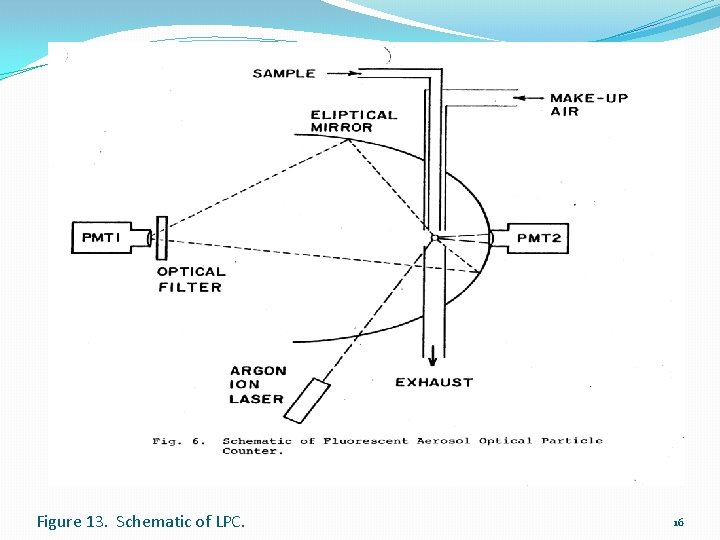
Figure 13. Schematic of LPC. 16

Cvnv(Xp) Ctru(Xp) EFF(Xp) = Ccnc(Xp) / Calgr(Xp) Figure 14. Overall schematic of the test setup. 17

Figure 15. The DMA. 18

This slide intentionally left blank. Originally it showed a commercial CNC. You can get on the web and find them. Look for Condensation Particle Counter or Condensation Nucleus Counter Figure 16. The CNC. 19

Figure 17. The top of the ALGR. 20

Figure 18. The switch box that allows choosing what controls the MFCs. 21

Figure 19. The LPC setting at the bottom of the ALGR.

Three pumps: AP 1 Laser Ptle Counter loop AP 2 Filtered air at top AP 3 Excess air at bottom MFC 2 Eight flows: Q 1 Excess at bottom Q 2 Filtered at top Q 3 LPC loop out Q 4 LPC loop Q 5 AP 2 make up Q 6 LPC loop in Q 9 LPC annular in Qsmt sample metering tube Q 1 – Q 9 ~ 1 to 4 L/m Qsmt ~ 0. 010 L/m Qsmt = 3. 55 * d. Psmt – 5. 42 d. Psmt ~ 1 inch H 2 O MFC 1 MFC 2 Figure 20. Alternating Gradient cloud chamber. Imperfect pumps will cause a variation of P that disturbs the d. Psmt. Hold d. Psmt very constant. Difficult. ! 23

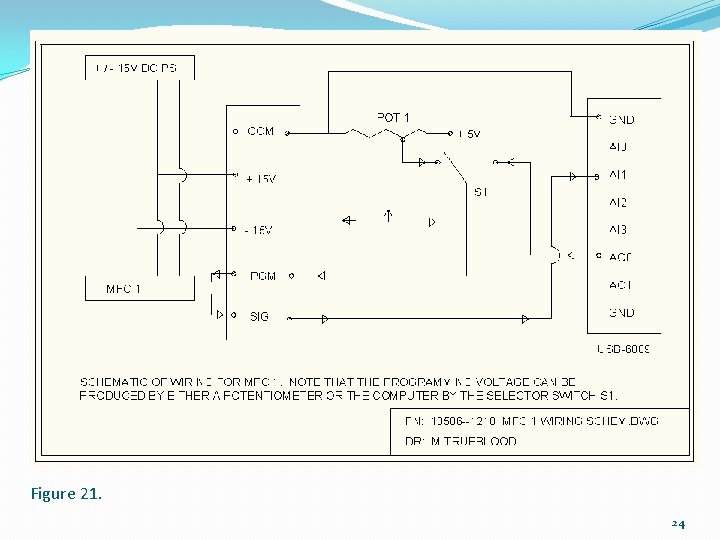
Figure 21. 24

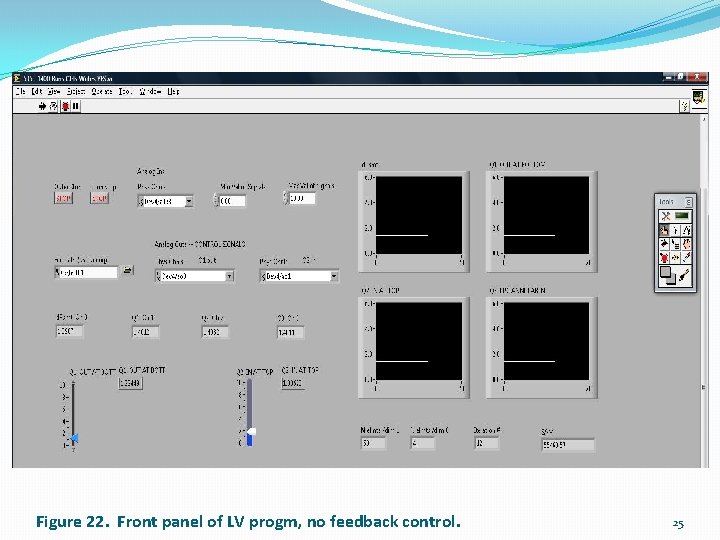
Figure 22. Front panel of LV progm, no feedback control. 25

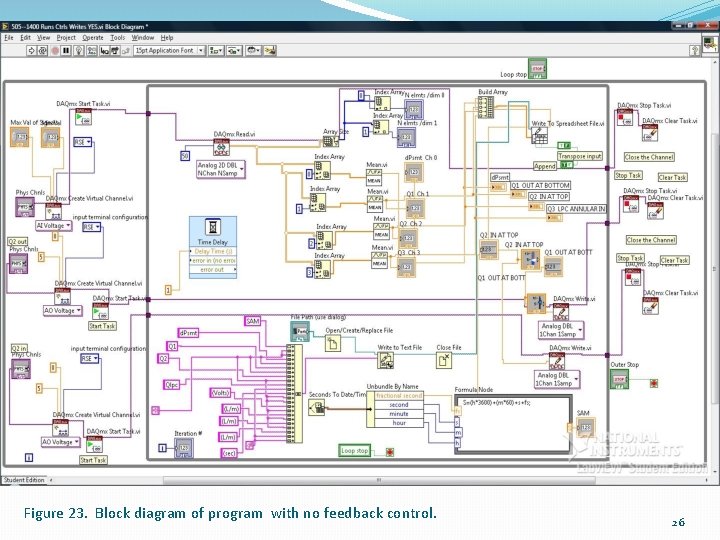
Figure 23. Block diagram of program with no feedback control. 26

The previous method allows one to control Q 1 (bottom outflow) a. Manually with the pot b. From labview program, but still manually. I would really like to keep d. Psmt constant. Thus a feedback loop that controls Q 1 based on comparing the actual d. Psmt to a set point value is what I really desire. 27

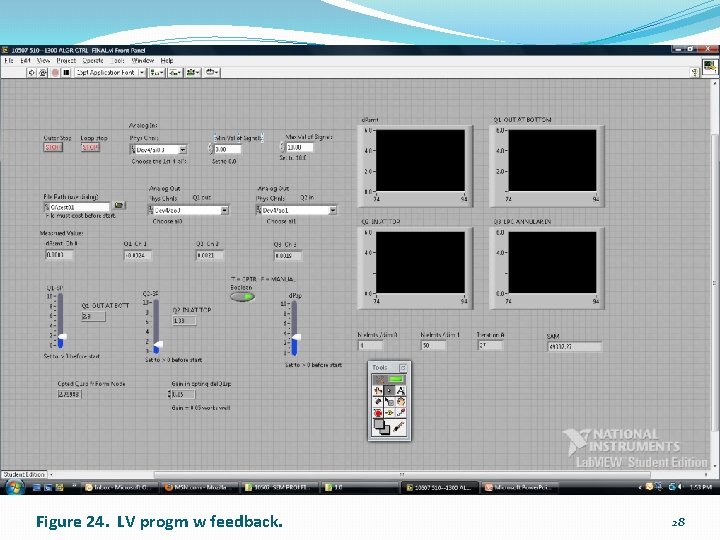
Figure 24. LV progm w feedback. 28

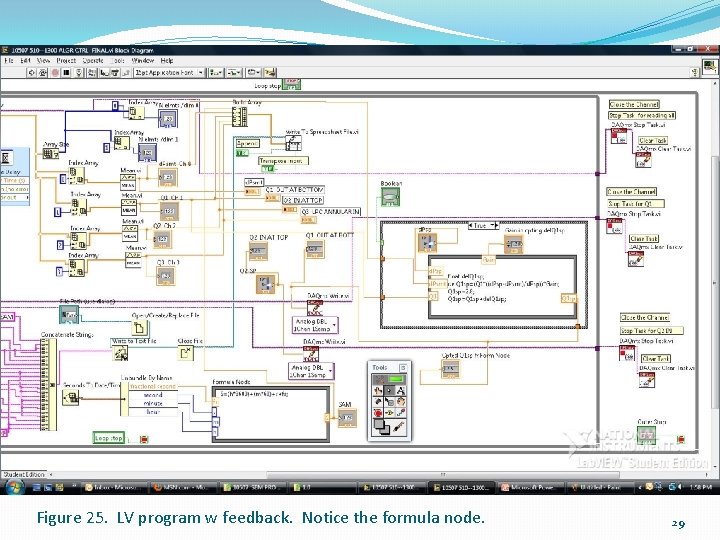
Figure 25. LV program w feedback. Notice the formula node. 29

Figure 26. Sample data, no feedback control. 30

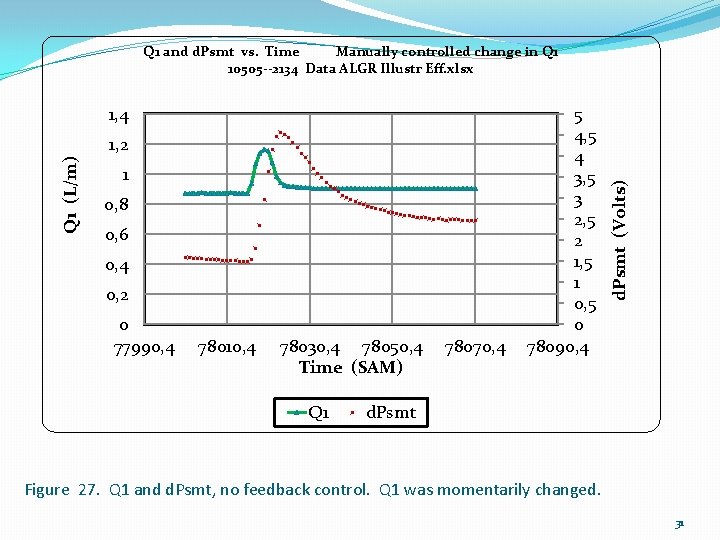
1, 4 Q 1 (L/m) 1, 2 1 0, 8 0, 6 0, 4 0, 2 0 77990, 4 78010, 4 78030, 4 78050, 4 Time (SAM) Q 1 78070, 4 5 4, 5 4 3, 5 3 2, 5 2 1, 5 1 0, 5 0 78090, 4 d. Psmt (Volts) Q 1 and d. Psmt vs. Time Manually controlled change in Q 1 10505 --2134 Data ALGR Illustr Eff. xlsx d. Psmt Figure 27. Q 1 and d. Psmt, no feedback control. Q 1 was momentarily changed. 31

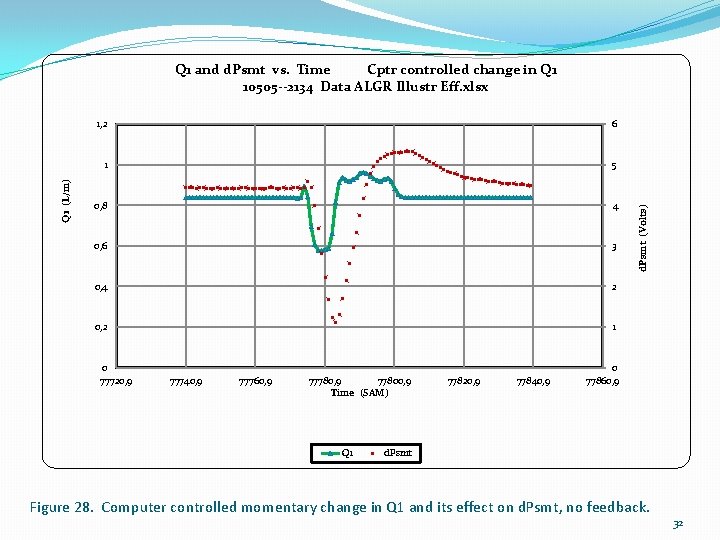
1, 2 6 1 5 0, 8 4 0, 6 3 0, 4 2 0, 2 1 0 77720, 9 77740, 9 77760, 9 77780, 9 77800, 9 Time (SAM) Q 1 77820, 9 77840, 9 d. Psmt (Volts) Q 1 (L/m) Q 1 and d. Psmt vs. Time Cptr controlled change in Q 1 10505 --2134 Data ALGR Illustr Eff. xlsx 0 77860, 9 d. Psmt Figure 28. Computer controlled momentary change in Q 1 and its effect on d. Psmt, no feedback. 32

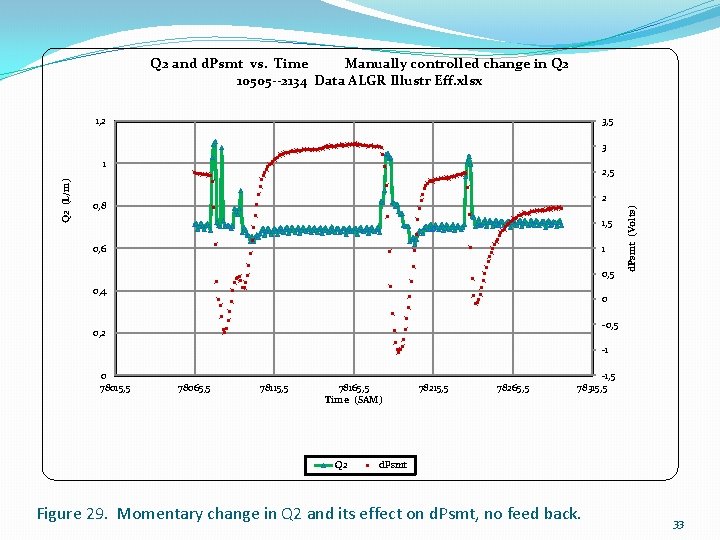
Q 2 and d. Psmt vs. Time Manually controlled change in Q 2 10505 --2134 Data ALGR Illustr Eff. xlsx 1, 2 3, 5 3 2, 5 2 0, 8 1, 5 0, 6 1 0, 5 0, 4 d. Psmt (Volts) Q 2 (L/m) 1 0 -0, 5 0, 2 -1 0 78015, 5 78065, 5 78115, 5 78165, 5 Time (SAM) Q 2 78215, 5 78265, 5 -1, 5 78315, 5 d. Psmt Figure 29. Momentary change in Q 2 and its effect on d. Psmt, no feed back. 33

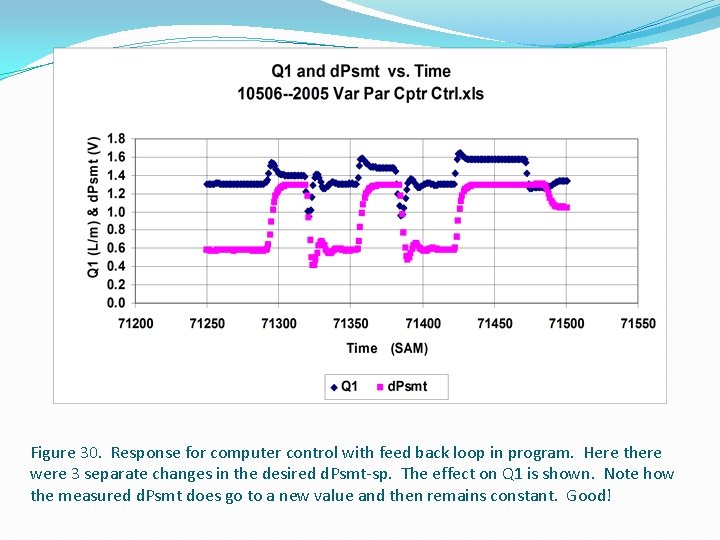
Figure 30. Response for computer control with feed back loop in program. Here there were 3 separate changes in the desired d. Psmt-sp. The effect on Q 1 is shown. Note how the measured d. Psmt does go to a new value and then remains constant. Good!

CONCLUSIONS 1. The output or signal of the MFCs has been successfully monitored by the labview program. 2. The MFCs have been successfully controlled a. manually with potentiometers. b. manually by the labview program. c. in an automated fashion with a closed loop feed back with the LV progm. 35

FURTHER WORK: 1. Have the LV program actually read the LPC, the d. Psmt, etc, and calculate the C (p/cc) as given by the ALGR. 2. Have the LV program read the CNC and log the Ccnc. 3. Have the LV program compute the EFF = [Ccnc / Calgr ]. 4. MFC 3 does not seem to provide a signal that I can monitor. Broken? I can control it, though, as proven by observing the rotameter in series with it. 5. Make use of all the logged data to find the “sweet spot” of operation of the ALGR where one gets reliable data. At this “sweet spot”, the Calgr would remain constant even though some of the flows wandered off their set points a small amount. 36

Acknowledgements: Thanks are due to Mr Mitch Cottrell and Mr Steven Achterberg for helpful suggestions. 37

QUESTIONS? 38

<end> 39