Active Contours Technique in Retinal Image Identification of

Active Contours Technique in Retinal Image Identification of the Optic Disk Boundary Soufyane El-Allali Stephen Brown Department of Computer Science and Engineering University of South Carolina Dr. Song Wang CSCE 790 Spring 2003

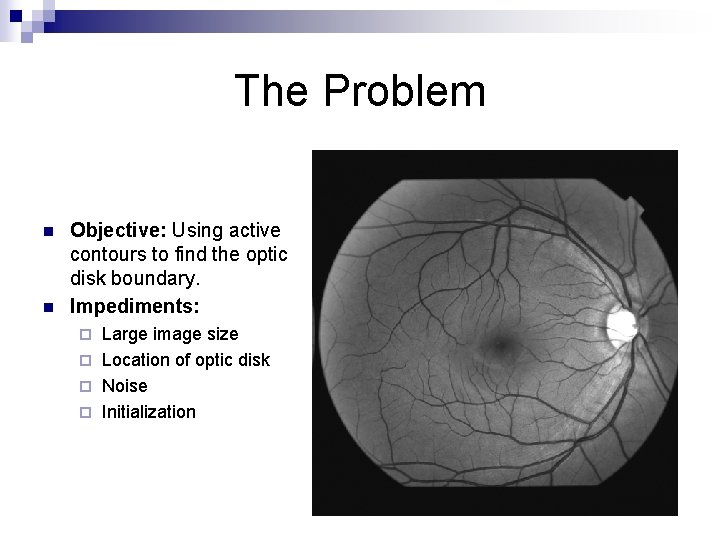
The Problem n n Objective: Using active contours to find the optic disk boundary. Impediments: Large image size ¨ Location of optic disk ¨ Noise ¨ Initialization ¨

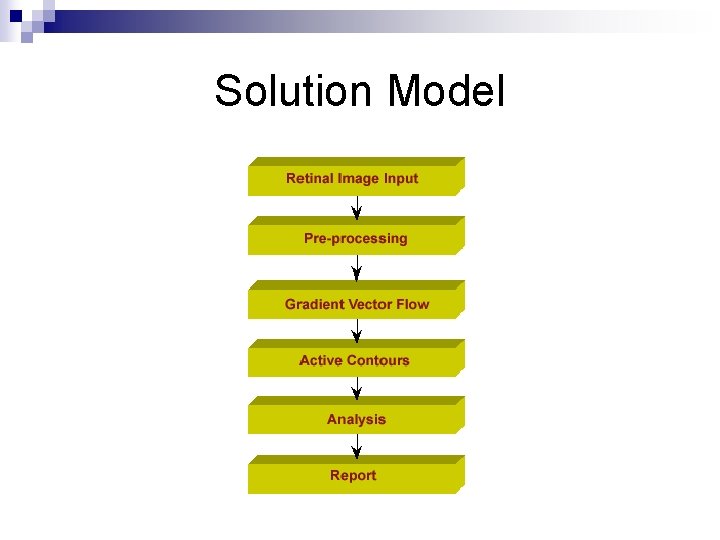
Solution Model

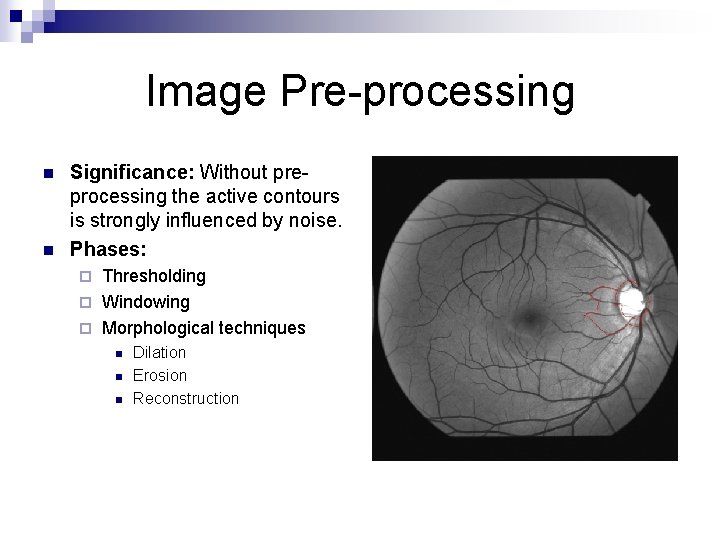
Image Pre-processing n n Significance: Without preprocessing the active contours is strongly influenced by noise. Phases: Thresholding ¨ Windowing ¨ Morphological techniques ¨ n n n Dilation Erosion Reconstruction

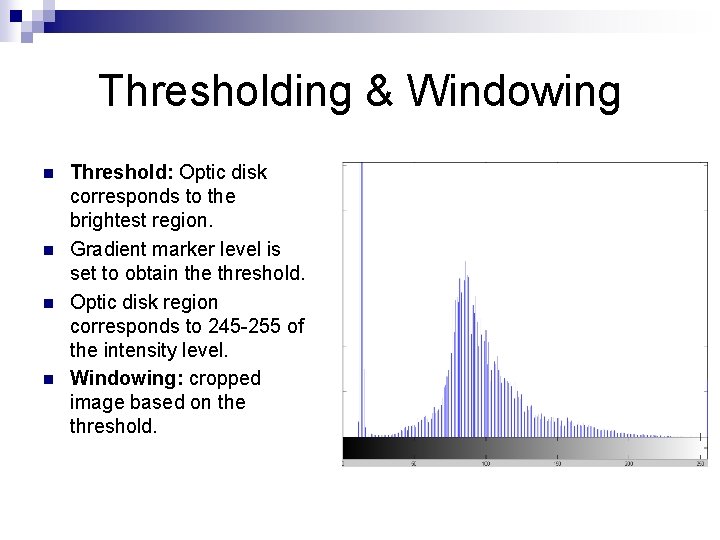
Thresholding & Windowing n n Threshold: Optic disk corresponds to the brightest region. Gradient marker level is set to obtain the threshold. Optic disk region corresponds to 245 -255 of the intensity level. Windowing: cropped image based on the threshold.

Dilation n Definition: Dilation causes objects to dilate or grow in size by adding pixels to the boundaries of object in an image. Dilation depends on a structure element. Dilation algorithm.

Erosion and Reconstruction n Definitions: Erosion causes objects to shrink by removing pixels on object boundaries. ¨ Reconstruction takes the maximum pixel value from the original image and the dilated/eroded image. ¨

Active Contours Revisted n Definition: Active contours (snakes) is an edge-based technique that defines curves within an image domain that can move under the influence of internal and external forces in order to achieve convergence along an object. is the snakes’ elasticity is the snakes’ regidity Gaussian function’s standard deviation

Active Contours Continued n Objective: minimizing the energy functional Solution: must satisfy Euler Lagrange’s Equation n Bringing the snakes to equalibrium: n ¨ n Adding a damping term and an inertial term Simple solution: using the gradient descent algorithm

Gradient Vector Flow (GVF) n n Traditional snakes: has a tendency not to converge in the case of concave shapes. GVF: Proposed by Xu and Prince Static external force h = (p, q) ¨ Minimizes the energy function ¨ n Solution: solving the Euler system is a regularization parameter

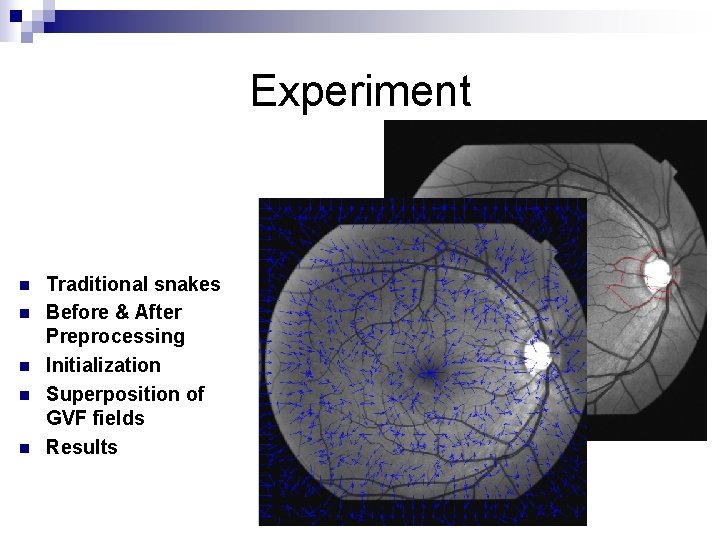
Experiment n n n Traditional snakes Before & After Preprocessing Initialization Superposition of GVF fields Results

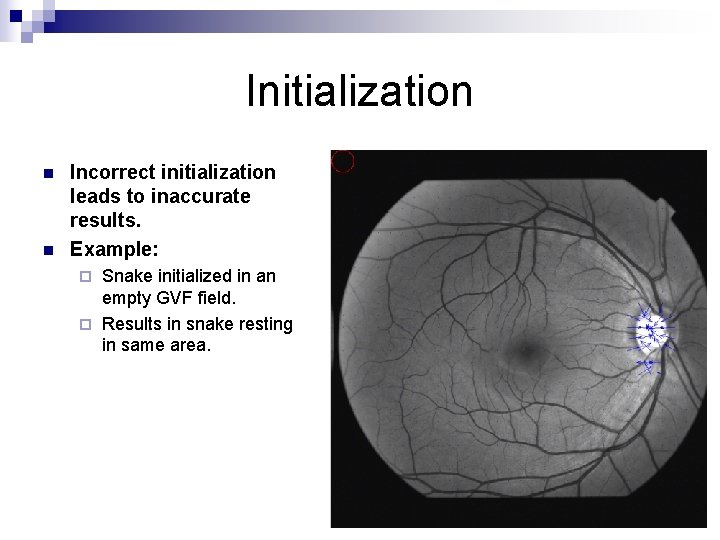
Initialization n n Incorrect initialization leads to inaccurate results. Example: Snake initialized in an empty GVF field. ¨ Results in snake resting in same area. ¨

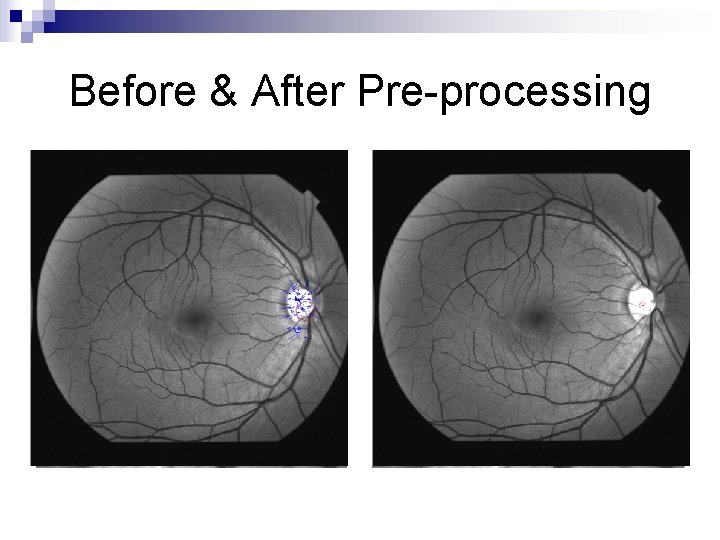
Before & After Pre-processing

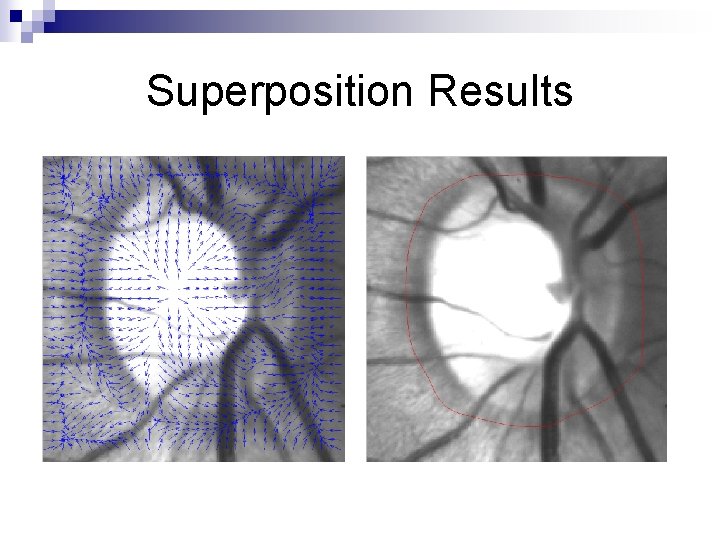
GVF fields Superposition n Motive: Larger Gaussian standard deviation captures the object of interests, yet blurring the edge boundary. ¨ Smaller Gaussian standard deviation stores the edge boundary, but does not capture the whole object of interest. ¨ n Solution: ¨ Superposing GVF fields with different Gaussian standard deviations.

Superposition Results

Demo

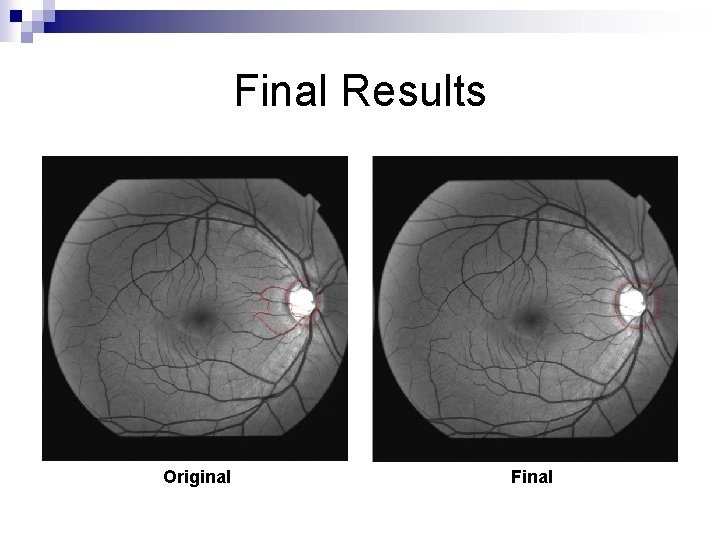
Final Results Original Final

Questions